Что означает цифра 0 в записи числа 5201

Что обозначает цифра 0 в записи числа?

Цифра «0» в записи числа обозначает отсутствие единиц какого-либо разряда.

Например, в числе 203 присутствуют 3 разряда: единицы, десятки и сотни. Десятки представлены в данном случае нулем. Число состоит из двух сотен и трех единиц.

Если рассмотреть число 230, то мы видим отсутствие единиц. Две сотни, три десятка, единиц нет.

0 в записи числа означает ноль, так как 0 равно 0).

Из этих трех цифр можно сложить довольно много трехзначных чисел м чтобы не запутаться. я бы предложил подбирать эти числа по следующей схеме:

ставим на первое место в трехзначном числе цифру 1 и начинаем считать

Столько же чисел получим, если поставим спереди цифру 2

Всего из этих трех цифр можно сложить 18 трехзначных чисел

Если это не номер телефона, и не номер ICQ.

Скорость света? Чисто графически похоже. И величина близка к скорости света.

Чертовски похоже на скорость света.

Цифры к нам пришли от Арабов. Если Вы заметете то первоначальное написание выглядело именно так (см рис.), а потом уже цифры стали писать как попало и кому как удобно. Изначально они писались строго палочками и черточками. Почему? Вот почему:

Два – сложенный вдвое;

Три – третий лишний (посмотрите на тройку на рисунке, там как будто бы она лишняя примкнула к двойке);

Четыре – четыре стороны света;

Пять – расстояние между пальцами;

Шесть – арабы пишут под углом, цифра «6» это отображение «9» письмо под уголом

Семь – от Арабского «сама» небо;

Восемь – равенство во всем;

Девять – срок беременности

Ноль – «цифер», ноль – пусто.

Примеры цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

или римские цифры: I V X L C D M.

А бывают: число π, e; комплексные числа, числа в 16-ричной системе счисления.

Источник

Чтение и запись натуральных чисел

Пройти тест по теме «Натуральные числа и действия над ними» можно по ссылке. Проверьте свои знания!

Для передачи на письме любого числа в понятном для всех виде, мы используем особые знаки, получившие название цифры.

Цифры – это особые знаки, которые мы используем для записи чисел.

Кроме самих знаков, нам понадобится система правил, которая описывает способ наименования и обозначения чисел. Она получила название система счисления или система записи чисел.

Система счисления – это набор правил, который описывает наименование и обозначение чисел на письме при помощи особых знаков: цифр.

Существует много систем счисления, но здесь мы будем рассматривать только ту, которую пользуемся каждый день.

Слово позиционная указывает на то, что значение, роль любой цифры, зависит от места ее расположения в числе.

Слово десятеричная означает, что любое натуральное число записывается на письме при помощи десяти особых символов, то есть, цифр, и их комбинаций:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Запись натурального числа – это его изображение на письме при помощи цифр и системы их записи.

Количество цифр, с помощью которых записано натуральное число, влияет на его название.

Число с тремя, четырьмя, пятью и более цифрами, соответственно, называется трехзначным, четырехзначным, пятизначным и т.д.

Таблица 1. Наибольшие и наименьшие натуральные однозначные и многозначные числа.

Цифра и число – это не одно и то же! Цифра – это всего лишь знак, при помощи которого мы можем записывать числа. Цифр всего лишь десять, а чисел – бесконечное множество. Число может быть записано при помощи цифр (182), и также при помощи слов (сто восемьдесят два).

Рассмотрим запись натурального числа более подробно.

В статье «Названия чисел до тысячи и более» подробно рассказано об устной нумерации чисел, поэтому здесь мы просто воспользуемся этими знаниями.

Запись натуральных чисел в десятеричной системе счисления

Для записи единиц, то есть, однозначного числа, в десятеричной системе счисления используются девять цифр:

нуль при этом означает отсутствие единиц в данной позиции.

Двухзначное число на записи обозначается при помощи приставления слева от цифры, обозначающей количество единиц в числе, соответствующей цифры, выражающей количество десятков единиц в данном числе.

Например, пятьдесят три, то есть, пять десятков и три единицы записывается на письме так: 53, а восемьдесят, то есть, восемь десятков и нуль единиц – 80.

Подобным образом формируется запись любого многозначного натурального числа. К примеру, шестьсот сорок два (шесть сотен, четыре десятка и две единицы) записывается как 642, а двенадцать тысяч пятьсот четыре (двенадцать тысяч, пять сотен, нуль десятков и четыре единицы) – как 12504.

Как вы видите, каждое место, на котором находится цифра, имеет свое особое значение, а именно:

Таблица 2. Значения цифр в зависимости от места в числе.

Таким образом, при записи натурального числа соблюдается следующее правило:

Если в любом числе взять произвольно две расположенные рядом цифры, то левая будет обозначать единицы, которые в десять раз больше, чем те, которые обозначает правая цифра.

Чтение натуральных чисел

Чтобы прочитать натуральное число любой длины, необходимо разбить его справа налево на группы из трех цифр (то есть, на классы), и назвать слева направо количество единиц каждого класса, прибавляя к ним название класса. При этом, не произносят название класса, не имеющего ни одной единицы.

Например, число 18.328.509.000.612 должно быть прочитано так: 18 триллионов 328 миллиардов 509 миллионов 612.

Название класса единиц также обычно не произносят.

Источник

Что означает число 000 в Ангельской нумерологии

Что означает число 000

Постоянное повторение числовых последовательностей в вашей жизни может означать, что вам приходит послание из мира духов и Ангелов. Эти числа называются ангельскими числами и могут предстать перед вами в любой форме. Существует бесконечное количество чисел Ангела и каждая комбинация имеет свой собственный смысл. Они скрывают в себе знания, руководство и поддержку. Вы можете научиться понимать, что означает каждое из них и расшифровывать послания, которые посылают вам ваши Ангелы.

Что означает число 000 в Ангельской нумерологии

Число “000” имеет в составе три цифры 0. То есть значение числа 0 усиливается в три раза. 0 – очень распространенное число, с которым мы часто сталкиваемся в повседневной жизни. Форма числа 0 имеет форму овала и смысл его – единство. В числе «000» заключено уникальное послание, посланное вашим Ангелом.

Число 0 наполнено божественной энергией и атрибутами бесконечности, связанными с Творцом. Также оно известно как Альфа и Омега всего сущего. Альфа означает начало, Омега означает конец. Ноль содержит свойства, объединяющее все цифры и является начальной точкой. Любое число, содержащее 0, делает вас на один шаг ближе к Творцу.

Символ “ничто” – это число 0, и оно означает, что вы должны освободиться от ограничений этого мира и освободить себя. Как только вы освободитесь, можете все начинать сначала (это еще одно свойство числа 0). Число “000” ангелов — это напоминание о том, что все во Вселенной взаимосвязано. И вы ничем не отличаетесь от других. Все ваши действия, слова и мысли зависят от позитивных и негативных вибраций внутри вас.

Поэтому вы должны принимать свои решения мудро и осторожно, чтобы не причинить вреда ни себе, ни окружающим вас людям. Когда три ноля сочетаются с любым другим числом, значение этого числа увеличивается трижды в смысле количества и качества. Энергия этого числа увеличивается, и следует точно знать, как три ноля действуют счастливым образом в каждый конкретный день.

Что делать, когда вы видите число 000

Известно, что “000” – это новые начинания, а новые начинания приходят с новыми возможностями и открывающимся потенциалом. Когда есть новое начало, вам всегда не будет хватать полной информации. Таким образом, вы должны быть очень осторожны с каждым решением, которое вы принимаете.

Когда вы встречаете число “000” Ангельской нумерологии, вам следует подумать о принятии решения, имея в виду его влияние на вашу жизнь. Одно решение может либо сделать ваш день, либо испортить его.

Во-первых, вы должны принять решение и попрощаться с существующей ситуацией и с нетерпением ждать того, что произойдет. Новая фаза жизни, в которую вы собираетесь вступить, будет находиться под присмотром помогающих вам Ангелов.

Число 0 будет опорой и защитником новой главы жизни, в которую вы собираетесь вступить. Как только вы полностью примете решение двигаться вперед, вы перестанете видеть число «000» и начнете видеть другие последовательности чисел, такие как 111, 222, 333 и так далее.

Но имейте в виду, если вы продолжаете встречать в жизни число «999» после того, как число «000» перестало появляться, вам нужно найти то, что все еще нуждается в решении и исцелении. «999» – это в основном напоминание Ангелам о том, что вы еще не все изменили в своей жизни. Очень часто, после того, как повторение числа Ангела «000» останавливается, «999» включается.

Поэтому оглянитесь вокруг и обратите внимание на то, что должно быть изменено в вашем окружении и жизни. Как только вы исправите это, и будете готовы к плаванию, повторение числа «999» также прекратиться.

Примеры появления числа Ангелов 000

Предположим, что вы живете в одном доме долгое время и все ваши друзья уже переехали из этого района. Вы чувствуете себя не очень хорошо, живя в одиночестве, и планируете съехать. Но не уверены, хорошо это или нет.

И вы начинаете сначала начнете видеть цифру “999”, которая означает, что вы узнали все, что можете, из текущей ситуации, и вам пора уходить. Затем начинает появляться число Ангела с номером “000”, которое подает сигнал, что вас ждут новые начинания и вам пора двигаться дальше. Когда вы видите цифру “000” несколько раз, принимайте решение мгновенно и не откладывайте свой отъезд. Чем больше вы медлите, тем больше вы пренебрегаете руководством Ангелов. А ведь вы не хотите этого делать?

Число Ангелов «000» знаменует начало и новый потенциал, которые ждут вас в вашей жизни. Это сигнал для вас, что пора принимать решения и двигаться дальше по жизни, чтобы исследовать новые возможности. Это шанс для вас, чтобы исследовать новый потенциал и узнать новые вещи. Не откладывайте принятие новых решений, когда число «000» появляется в вашей жизни постоянно!

Источник

Значимые цифры: правила, примеры, решенные упражнения

Содержание:

А что происходит, когда число целое? Это означает, что он известен с максимально возможной точностью, другими словами, он имеет бесконечную точность. Например, при подсчете людей, животных или таких предметов, как книги и телефоны, результатом будет точное целое число.

Если мы скажем, что в кинотеатре 110 человек смотрят фильм, это точное число, ни много, ни мало, и оно состоит из трех значащих цифр.

Значительные числа обрабатываются по некоторым простым правилам, которые запоминаются после небольшой практики, как мы увидим дальше.

Правила определения значащих цифр числа

Правило 1

Начальные нули не считаются значащими цифрами, поэтому 0,045 и 4,5 имеют две значащие цифры, поскольку они начинают отсчет слева и начиная с первой ненулевой цифры.

Правило 2

Нули после (справа) первой значащей цифры действительно считаются значащей цифрой (если это оправдано точностью измерительного прибора).

Наконец, нули в середине также считаются значащей цифрой.

Правило 3

Для чисел, записанных в экспоненциальном представлении, все цифры в мантиссе значимы, а показатель степени не влияет на точность.

Правило 4

При выполнении операций с десятичными знаками, например при вычислении площадей или других подобных операций, результат должен иметь такое же количество значащих цифр, что и количество с наименьшим количеством значащих цифр, участвовавших в операции. Это правило действует для любых арифметических операций.

Правило 5

Знак числа не влияет на количество его значащих цифр.

Мы сразу же увидим некоторые примеры этого и всех других правил.

Примеры

Пример 1

Найдите, сколько значащих цифр в каждом из этих чисел.

Ответы

а) 876 имеет 3 значащих цифры.

б) 1000,68 имеет 6 значащих цифр, поскольку нули в середине считаются как таковые.

c) Вместо 0,00005026 имеется 4 значащих цифры. Обратите внимание, что 5 нулей слева от 5 не считаются значащими цифрами, тогда как 0 между 5 и 2 считается.

г) 4.8 имеет 2 значащих цифры.

Пример 2

Обычно измерения проводят с помощью измерительных инструментов, таких как рулетки, часы, термометры, весы и т. Д. Со сколькими значащими цифрами мы должны указывать количества, которые мы измеряем таким образом?

Ответить

Это зависит от оценки инструмента, которым он измеряется. Возьмем пример: измерьте внешний диаметр трубы с помощью градуированной линейки и штангенциркуля.

Он более точен, чем градуированная линейка, потому что с его помощью мы можем узнать более значащие числа определенной длины.

Вот почему нет смысла сообщать периметр, скажем, 35,88 см, если мы измеряем его рулеткой, поскольку этот инструмент недостаточно точен, чтобы указать такое количество значащих цифр.

Оценка рулетки A определяется по:

Пример 3

Сколько значащих цифр в показании цифрового термометра?

Ответить

Термометр на рисунке показывает трехзначные показания температуры. Однако в показанном измерении 36,6 ºC только первые две цифры слева направо являются точными, поскольку на десятичную дробь влияет погрешность оценки прибора, которая обычно указывается на задней стороне прибора или на ваше руководство по эксплуатации.

Обычно для представленного типа цифрового прибора погрешность оценки составляет 0,1 ºC. Этого достаточно, чтобы быть уверенным, что у вас нет температуры.

Правила округления чисел

При использовании калькулятора для выполнения расчетов с полученными измерениями некорректно давать результат, используя все цифры, которые появляются на экране.

Сохраняются только те, которые точно известны, поскольку только они имеют истинное значение. Затем необходимо округлить результаты, чтобы они соответствовали количеству точно известных цифр. Вот эти правила:

-Если число, следующее за цифрой, которую необходимо скрыть, является равно или больше 5, к этой цифре добавляется 1.

Например, при округлении 3,786 до двух десятичных знаков мы хотим сохранить числа до 8. Поскольку число, следующее за (6), больше 5, 8 становится 8 + 1 = 9, и число остается как 3.79.

-Когда число, следующее за цифрой, которую необходимо сохранить, менее 5, цифра останется прежней.

Если мы хотим округлить 1,27924, чтобы у него было только 3 десятичных разряда, это достигается путем достижения 9, за которым следует 2. Поскольку 2 меньше 5, эти десятичные дроби исчезают, а округленное число остается 1,279.

Упражнение решено

Обеденный стол имеет форму и размеры, указанные на прилагаемом рисунке. Вам предлагается рассчитать его площадь по правилам работы со значащими цифрами.

Решение

Зона стола может быть разделена на центральную прямоугольную зону и два полукруга, по одному с каждой стороны, которые вместе составляют один полный круг.

Мы будем называть A₁ к площади прямоугольника, задаваемой:

К₁ = основание × высота = 2,5 м x 1,0 м = 2,5 м 2

Со своей стороны, площадь круга, равная площади 1 полукруга, умноженной на 2, равна:

Диаметр любого из полукругов составляет 1,0 м, поэтому радиус равен 0,50 м. Диаметр также можно использовать напрямую для расчета площади, в этом случае:

К₂ = (π × диаметр 2 ) / 4

К₂ = [π x (1,0 м) 2 ] / 4 = 0,785398163 м 2

Были использованы все цифры, предоставленные калькулятором. Теперь добавляем A₁ уже₂ для общей площади стола A:

A = (2,5 + 0,785398163) м 2 = 3,285398163 м 2

Поскольку размеры таблицы известны до двух значащих цифр, не имеет смысла выражать результат со всеми десятичными знаками, указанными калькулятором, который никогда не дает количество значащих цифр в результате.

Что вам нужно сделать, так это округлить область так, чтобы в ней было такое же количество значащих цифр, что и размеры таблицы, то есть 2. Таким образом, окончательный результат будет представлен следующим образом:

Ссылки

Эктодерма: части, производные и изменения

Страх взросления (у детей и взрослых): почему возникает и каковы его симптомы?

Источник

Как округлить до трех значащих цифр

имеет три значащие цифры;

имеет две значащие цифры;

имеет три значащие цифры;

имеет три значащие цифры;

имеет две значащие цифры.

1.2. Когда необходимо указать, что число является точным, после числа должно быть указано слово «точно» или же последняя значащая цифра печатается жирным шрифтом

Пример. В печатном тексте:

1 кВт·ч = 3 600 000 Дж (точно), или = 3600000 Дж

1.3. Следует различать записи приближенных чисел по количеству значащих цифр.

1. Следует различать числа 2,4 и 2,40. Запись 2,4 означает, что верны только цифры целых и десятых; истинное значение числа может быть например 2,43 и 2,38. Запись 2,40 означает, что верны и сотые доли числа; истинное число может быть 2,403 и 2,398, но не 2,421 и не 2,382.

Утвержден Постоянной Комиссией по стандартизации
Улан-Батор, июнь 1977 г.

1.4. Число, для которого указывается допускаемое отклонение, должно иметь последнюю значащую цифру того же разряда как и последняя значащая цифра отклонения.

1.5. Числовые значения величины и ее погрешности (отклонения) целесообразно записывать с указанием одной и той же единицы физических величин.

Пример. 80,555±0,002 кг

1.6. Интервалы между числовыми значениями величин следует записывать:

От 60 до 100 или от 60 до 100

Свыше 100 до 120 или свыше 100 до 120

Свыше 120 до 150 или свыше 120 до 150.

1.7. Числовые значения величин должны указываться в стандартах с одинаковым числом разрядов, которое необходимо для обеспечения требуемых эксплуатационных свойств и качества продукции. Запись числовых значений величин до первого, второго, третьего и т. д. десятичного знака для различных типоразмеров, видов марок продукции одного названия, как правило, должна быть одинаковой. Например, если градация толщины стальной горячекатаной ленты 0,25 мм, то весь ряд толщин ленты должен быть указан с точностью до второго десятичного знака.

В зависимости от технической характеристики и назначения продукции количество десятичных знаков числовых значений величин одного и того же параметра, размера, показателя или нормы может иметь несколько ступеней (групп) и должно быть одинаковым только внутри этой ступени (группы).

2.1. Округление числа представляет собой отбрасывание значащих цифр справа до определенного разряда с возможным изменением цифры этого разряда.

Пример. Округление числа 132,48 до четырех значащих цифр будет 132,5.

2.2. В случае, если первая из отбрасываемых цифр (считая слева направо) меньше 5, то последняя сохраняемая цифра не меняется.

Пример. Округление числа 12,23 до трех значащих цифр дает 12,2.

2.3. В случае, если первая из отбрасываемых цифр (считая слева направо) равна 5, то последняя сохраняемая цифра увеличивается на единицу.

Пример. Округление числа 0,145 до двух значащих цифр дает 0,15.

Примечание. В тех случаях, когда следует учитывать результаты предыдущих округлений, следует поступать следующим образом:

1) если отбрасываемая цифра получилась в результате предыдущего округления в большую сторону, то последняя сохраняемая цифра сохраняется;

Пример. Округление до одной значащей цифры числа 0,15 (полученного после округления числа 0,149) дает 0,1.

2) если отбрасываемая цифра получилась в результате предыдущего округления в меньшую сторону, то последняя оставшаяся цифра увеличивается на единицу (с переходом при необходимости в следующие разряды).

Пример. Округление числа 0,25 (полученного в результате предыдущего округления числа 0,252) дает 0,3.

2.4. В случае, если первая из отбрасываемых цифр (считая слева направо) больше 5, то последняя сохраняемая цифра увеличивается на единицу.

Пример. Округление числа 0,156 до двух значащих цифр дает 0,16.

2.5. Округление следует выполнять сразу до желаемого количества значащих цифр, а не по этапам.

Пример. Округление числа 565,46 до трех значащих цифр производится непосредственно на 565. Округление по этапам привело бы к:

565,46 в I этапе – к 565,5,

а во II этапе – 566 (ошибочно).

2.6. Целые числа округляют по тем же правилам, как и дробные.

1. Автор – делегация ВНР в Постоянной Комиссии по стандартизации.

3. Стандарт СЭВ утвержден на 41-м заседании ПКС.

4. Сроки начала применения стандарта СЭВ:

Срок начала применения стандарта СЭВ в договорно-правовых отношениях по экономическому и научно-техническому сотрудничеству

Срок начала применения стандарта СЭВ в народном хозяйстве

Определение 1.6. Значащими цифрами в записи приближенного числа называются:

– все ненулевые цифры;

– нули, содержащиеся между ненулевыми цифрами;

– нули, являющиеся представителями сохраненных десятичных разрядов при округлении.

В следующих примерах значащие цифры подчеркнуты.

Пример 1.6. 2.305; 0.0357; 0.001123; 0.035299879 = 0.035300.

При округлении числа 0.035299879 до шести знаков после запятой получается число 0.035300, в котором последние два нуля являются значащими. Если отбросить эти нули, то полученное число 0.0353 не является равнозначным с числом 0.035300 приближенным значением числа 0.035299879, так как погрешности указанных приближенных чисел отличаются.

Определение 1.7. Первые n значащих цифр в записи приближенного числа называются верными в узком смысле, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего n-й значащей цифре, считая слева направо.

Наряду с данным определением иногда используется другое.

Определение 1.8. Первые n значащих цифр в записи приближенного числа называются верными в широком смысле, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего n-й значащей цифре.

Пример 1.7. Определить верные цифры приближенного значения а_p = 2.721 числа е, если известно, что е = = 2.718281828.

б) скорость света в вакууме С = 3.00 • 10 8 м/с;

Замечание. Термин «верные значащие цифры» нельзя понимать буквально. Например, современное опытное значение скорости света в вакууме составляет С = 2.997925 • 10 8 м/с. Очевидно, что ни одна значащая цифра в примере 1.9, б не совпадает с соответствующей точной цифрой, но абсолютная погрешность меньше половины разряда, соответствующего последней значащей цифре в записи 3.00 • 10 8 :

Правило округления чисел

Чтобы округлить число до n значащих цифр, отбрасывают все цифры, стоящие справа от n-й значащей цифры, или, если это нужно для сохранения разрядов, заменяют их нулями. При этом:

1) если первая отброшенная цифра меньше 5, то оставшиеся десятичные знаки сохраняют без изменения;

2) если первая отброшенная цифра больше 5, то к последней оставшейся цифре прибавляют единицу;

3) если первая отброшенная цифра равна 5 и среди остальных отброшенных цифр есть ненулевые, то к последней оставшейся цифре прибавляют единицу;

4) если первая из отброшенных цифр равна 5 и все отброшенные цифры являются нулями, то последняя оставшаяся цифра оставляется неизменной, если она четная, и увеличивается на единицу, если – нечетная (правило четной цифры).

Это правило гарантирует, что сохраненные значащие цифры числа являются верными в узком смысле, т. е. погрешность округления не превосходит половины разряда, соответствующего последней оставленной значащей цифре. Правило четной цифры должно обеспечить компенсацию знаков ошибок.

Пример 1.10. Приведем примеры округления до четырех значащих цифр:

Δ_p = |3.142 – 3.1415926| 8 = 2.998 • 10 8 ;

Следующая теорема выявляет связь относительной погрешности числа с числом верных десятичных знаков.

Теорема 1.1. Если положительное приближенное число имеет n верных значащих цифр, то его относительная погрешность δ не превосходит величины 10 1- n деленной на первую значащую цифру α_n,:

Формула (1.11) позволяет вычислить предельную относительную погрешность

а) Здесь n = 4, α_n = 3. Используем формулу (1.12) для оценки относительной погрешности: δ =10 1- n / α_n = 0.001/3 ≈ 0.00033.

Для определения абсолютной погрешности применим формулу (1.10):

б) Аналогично вычислим: n = 7, α_n = 2, δ_а = 10 1- n / α_n = 0.000001/2 = 0.0000005;

Δ_a = |а_р| δ_а = 2.997925 10 8 • 0.0000005 ≈ 150.

В некоторых финансовых отчетах данные показателей представлены с точностью округления до определенных значащих цифр. Что значит значащая цифра? Дело в том, что при визуальном анализе презентаций отчетов с миллионами не нужно засорять точными числовыми значениями отображая каждую цифру в числе (единицы, десятки, сотни и тысячи), чтобы не ухудшить читабельность данных.

Как округлить до трех значащих цифр в Excel

В Excel все решает пользователь. Программа округлит дробные или даже целые числа в зависимости какое число значащих цифр удовлетворит потребность пользователя. Несомненно, на первый взгляд такое округление может вызывать сомнение в рациональности решения. Однако в презентациях есть место быть как точным показателям, так и относительным. И в других ситуациях это также применимо. Например, в стратегическом планировании более важные относительные показатели, так как сколько не планируй никогда не угадаешь точные результирующие числа. В тактическом планировании более важны точные значения чтобы избежать серьезных просчетов. В стратегическом планировании где показатели достигают миллионов, каждое значение ниже определенного числа значащих цифр – не существенно.

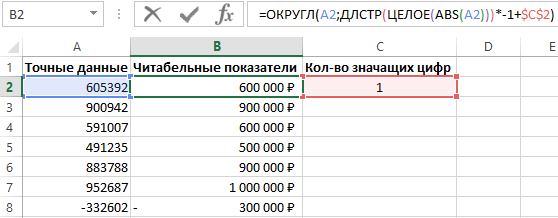
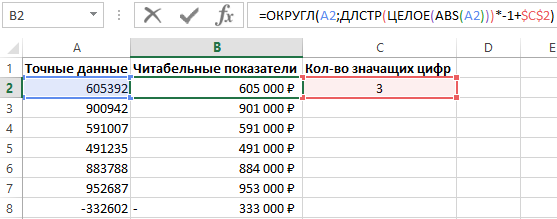
Ниже на рисунке показано, как составить формулу, которая округляет миллионные числовые значения до заданного числа значащих цифр:

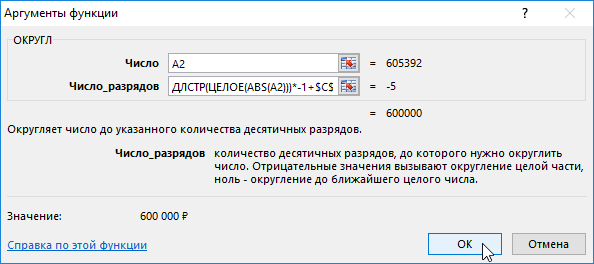
Функция ОКРУГЛ используется для округления исходного числового значения до определенного количества разрядов после запятой. Функция содержит 2 аргумента:

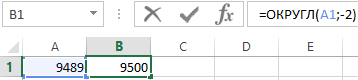
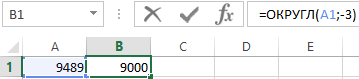
Если во втором аргументе функции ОКРУГЛ указать отрицательное число, тогда Excel округлит исходное числовое значение в соответствии цифр по левой стороне запятой. Например, следующая формула возвращает в результате вычисления число 9500:

Такая формула прекрасно работает, но не всегда. Например, что будет если исходные числовые значения будут разных величин числовых радов? Одни будут более миллиона, другие едва превышают сотни тысяч. Если возникнет необходимость округлить все такие исходные значения до одной и той же значащей цифры используя при этом одну и туже формулу (как обычно принято в Excel). Применять для отдельных групп исходных значений функцию ОКГРУГЛ с разными значениями в аргументах – это не правильное, а точнее не наилучшее решение. Хотя теоретически все может сработать.

Для красивого решения данной задачи следует использовать постоянное неизменяемое число значащих цифр в формуле, которая вычислит соответствующие значения.

Как узнать количество значащих цифр в Excel

Данная формула сначала преобразовывает заданное исходное отрицательно число в положительное используя функцию ABS (уберет знак минус спереди при его наличии). Полученный результат далее обрабатывается функцией ЦЕЛОЕ, котаря убирает все разряды после запятой. Далее полученный результат обрабатывается функцией ДЛСТР с целью подсчета количества символов из которых состоит исходное числовое значение без знака минуса и запятой.

Округляем до 3 значащих цифр в Excel

Число 2 указанное в аргументе данной формулы можно заменить на ссылку с ячейкой в которой будет указано желаемое число заданных значащих цифр пользователем. Как на рисунке с примером.

Таким образом можно округлить до 3 или 5 значащих цифр. Просто укажите необходимое значение в ячейке C2.

Источник