Что означает тройной знак равенства
Операторы сравнения в JavaScript: тройной знак равенства и двойной знак равенства
Вы видели двойные и тройные знаки равенства в JavaScript. Но что они? Если коротко: == преобразует тип, а === не преобразует тип.
Двойной знак равенства (==) проверяет только равенство значений. Он выполняет приведение типов. Это означает, что перед проверкой значений он преобразует типы переменных, чтобы привести их в соответствие друг к другу.
Тройной знак равенства (===) не выполняет приведение типов. Он проверяет, имеют ли сравниваемые переменные одинаковое значение и тип.
Рассмотрим несколько примеров:
Пример 1
Значение и тип у foo и bar одинаковые. Поэтому результат для обоих — true.
Пример 2
Значения number и stringNumber выглядят одинаковыми. Но number имеет тип Number, а stringNumber имеет тип string. Даже если значения переменных одинаковы, тип не совпадает. Поэтому оператор == возвращает значение true. Но при проверке значения и типа значение равно false.
Пример 3
Значение 0 при проверке с false является тем же. 0 и false имеют одинаковое значение для JavaScript. Но при проверке с помощью тройного оператора значение ложно, потому что 0 имеет тип number, а false – boolean.
Пример 4
Значение пустой строки и false – это в JavaScript то же самое. Следовательно, == возвращает значение true. Но тип переменных отличается, поэтому === возвращает значение false.
Когда использовать ==, а когда ===?
Если есть сомнения, используйте ===. Это избавит вас от большого количества потенциальных ошибок.
Если не нужен контроль входящих данных, используйте ==. Например, если API принимает от клиента «true» и true, используйте ==.
Эта таблица показывает, насколько сложно сравнение в JavaScript.
Дайте знать, что вы думаете по данной теме в комментариях. За комментарии, лайки, дизлайки, отклики, подписки низкий вам поклон!
Пожалуйста, опубликуйте ваши мнения по текущей теме материала. За комментарии, отклики, лайки, подписки, дизлайки низкий вам поклон!
Таблица истинности тройное равно
| Клавиша | Оператор | |
|---|---|---|
| ! | ¬ | Отрицание (НЕ) |
| | | | | Штрих Шеффера (И-НЕ) |
| # | ↓ | Стрелка Пирса (ИЛИ-НЕ) |
| * | & | Конъюнкция (И) |
| + | v | Дизъюнкция (ИЛИ) |
| ^ | ⊕ | Исключающее ИЛИ, сумма по модулю 2 (XOR) |
| @ | → | Импликация (ЕСЛИ-ТО) |
| % | ← | Обратная импликация |
| = | ≡ ( |
bc необходимо ввести так: a*b*c+a*b=c+a=b*c
Для ввода данных в виде логической схемы используйте этот сервис.
Правила ввода логической функции
Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Если число высказываний в логическом выражении N, то таблица истинности будет содержать 2 N строк, так как существует 2 N различных комбинаций возможных значений аргументов.
| Эквиваленция | |
|---|---|
| Исключающее ИЛИ-НЕ, EQ, XNOR | |
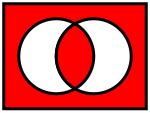 Диаграмма Венна | |
| Определение | x = y  |
| Таблица истинности | ( 1001 )  |
| Логический вентиль |  |
| Нормальные формы | |
| Дизъюнктивная | x ⋅ y + x ¯ ⋅ y ¯ >cdot >>  |
| Конъюнктивная | ( x ¯ + y ) ⋅ ( x + y ¯ ) >+y)cdot (x+ >)>  |
| Полином Жегалкина | 1 ⊕ x ⊕ y  |
| Принадлежность предполным классам | |
| Сохраняет 0 | Нет |
| Сохраняет 1 | Да |
| Монотонна | Нет |
| Линейна | Да |
| Самодвойственна | Нет |
Логическая равнозначность или эквивале́нция (или эквивале́нтность [1] ) — это логическое выражение, которое является истинным тогда, когда оба простых логических выражения имеют одинаковую истинность. Двуместная логическая операция обычно обозначается символом ≡ или ↔.
Эквиваленция A ⟺ B 
Задаётся следующей таблицей истинности:
Таким образом, высказывание A ≡ B означает «A то же самое, что B», «A эквивалентно B», «A тогда и только тогда, когда B».
Не надо путать эквиваленцию — логическую операцию с логической эквивалентностью [en] высказываний — бинарным отношением. Связь между ними следующая:
Логические выражения A
и B
эквивалентны в том и только в том случае, когда эквиваленция A ⟺ B
истинна при всех значениях логических переменных.
| Клавиша | Оператор | |
|---|---|---|
| ! | ¬ | Отрицание (НЕ) |
| | | | | Штрих Шеффера (И-НЕ) |
| # | ↓ | Стрелка Пирса (ИЛИ-НЕ) |
| * | & | Конъюнкция (И) |
| + | v | Дизъюнкция (ИЛИ) |
| ^ | ⊕ | Исключающее ИЛИ, сумма по модулю 2 (XOR) |
| @ | → | Импликация (ЕСЛИ-ТО) |
| % | ← | Обратная импликация |
| = | ≡ ( |
bc необходимо ввести так: a*b*c+a*b=c+a=b*c
Для ввода данных в виде логической схемы используйте этот сервис.
Правила ввода логической функции
Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Если число высказываний в логическом выражении N, то таблица истинности будет содержать 2 N строк, так как существует 2 N различных комбинаций возможных значений аргументов.
Понятие равенства, знак равенства, связанные определения
Материал статьи позволит ознакомиться с математической трактовкой понятия равенства. Порассуждаем на тему сути равенства; рассмотрим его виды и способы его записи; запишем свойства равенства и проиллюстрируем теорию примерами.
Что такое равенство
Само понятие равенства тесно переплетено с понятием сравнения, когда мы сопоставляем свойства и признаки, чтобы выявить схожие черты. Процесс сравнения требует наличия двух объектов, которые и сравниваются между собой. Данные рассуждения наводят на мысль, что понятие равенства не может иметь место, когда нет хотя бы двух объектов, чтобы было что сравнивать. При этом, конечно, может быть взято большее количество объектов: три и более, однако, в конечном, счете, мы так или иначе придем к сравнению пар, собранных из заданных объектов.
Смысл понятия «равенство» в обобщенном толковании отлично определяется словом «одинаковые». О двух одинаковых объектах можно говорить – «равные». Например, квадраты 

Говоря о равенстве, мы можем иметь в виду как объекты в целом, так и их отдельные свойства или признаки. Объекты являются равными в целом, когда одинаковы по всем характеристикам. Например, когда мы привели в пример равенство квадратов, имели в виду их равенство по всем присущим им свойствам: форме, размеру, цвету. Также объекты могут и не быть равными в целом, но обладать одинаковыми отдельными признаками. Например: 

Таким образом, необходимо заранее понимать, равенство какого рода мы имеем в виду.
Запись равенств, знак равно
Равенство – запись, в которой использован знак равно, разделяющий два математических объекта (или числа, или выражения и т.п.).
Верные и неверные равенства
Составленные равенства могут соответствовать сути понятия равенства, а могут и противоречить ему. По этому признаку все равенства классифицируют на верные равенства и неверные равенства. Приведем примеры.
Свойства равенств
Запишем три основных свойства равенств:
Буквенно сформулированные свойства запишем так:
Отметим особенную пользу второго и третьего свойств равенств – свойств симметричности и транзитивности – они дают возможность утверждать равенство трех и более объектов через их попарное равенство.
Двойные, тройные и т.д. равенства
При помощи таких цепочек равенств оптимально составлять равенство трех и более объектов. Такие записи по своему смыслу являются обозначением равенства любых двух объектов, составляющих исходную цепочку равенств.
Составляя подобные цепочки, удобно записывать последовательность решения примеров и задач: такое решение становится наглядным и отражает все промежуточные этапы вычислений.
Двойной и тройной операторы равенства == и === Примеры
До этого момента мы имели дело только с операторами сравнения, которые использовались для принятия решений при работе с конструкциями if-else. При этом преимущественно использовался оператор >= больше или равно.
Для этого существую различные операторы равенства.
Рассмотрим пример использования оператора тройного равенства в JavaScript и потом прокомментируем его.
Пример 1.1
Блок if в одну строку
Оптимизируем код примера 1.1
Пример 1.2
Пример 1.3
Как работает тройной оператор равенства
Для удобства можно перейти непосредственно в консоль и продемонстрировать еще раз работу оператора тройного равенства.
Двойное равенство ==
Свободный оператор равенства == (два знака равно) проводит приведение типов. Вернемся снова в консоль.
Пример 2.1
Пример 2.2
Продолжим работать с примером №1
Пример 1.4
Пример 1.5
Всегда строгое равенство ===
Это означает, что использование оператора двойного равенства может привести к появлению многих труднодоступных ошибок в вашем коде.
Поэтому одним из главных правил написания чистого кода является: избегать использовать оператор двойного равенства насколько это возможно.
Некоторые всегда по умолчанию используют тройной оператор равенства и делают вид, что это единственный из существующих вариантов. Так будем делать и мы. Хотя о двойном операторе равенства мы еще поговорим.
Далее рассмотрим другие примеры.
Примеры использования двойного и тройного равенства
Рассмотрим пример, когда значения приходят с веб-страницы. Для этого мы будем использовать функцию prompt (понятие функций мы будем рассматривать в следующем разделе).
Пример 3.1
Этот код будет вызывать окно с полем для ввода информации.
Пример 3.2
Таким образом, переменная favorite будет содержать значение, которое мы введем в поле для ввода, вызванное функцией prompt. Это значение можно как-то использовать. Например, вывести его в консоль.
Пример 3.3
Пример 3.4
Пример 3.5
Пример 3.6
Пробуем в поле для ввода ввести другое число, например 22:
Несколько условий одновременно
Пример 4.1
В целом такая конструкция с несколькими блоками if (с несколькими условиями) работает так : сначала выполняется проверка условия первого блока if. Если первая проверка не проходит, выполняется проверка условия второго блока if. Если эта проверка проходит, то выполняется код второго блока if.
Пример 4.2
На практике подобные конструкции if-else с составлением нескольких условий (несколько блоков if), время от времени используются.
Операторы неравенства
Пример 4.3
11 is also cool number
Равенство и неравенство. Знаки: больше, меньше, равно
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Математические знаки
Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:
Символ меньше (
Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:
Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:
Равенство и неравенство
Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.
Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».
Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.
Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн-формате. Как найти знаки на клавиатуре? Ответ на картинке:



