Что означает треугольник в физике 7 класс
Сила упругости
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
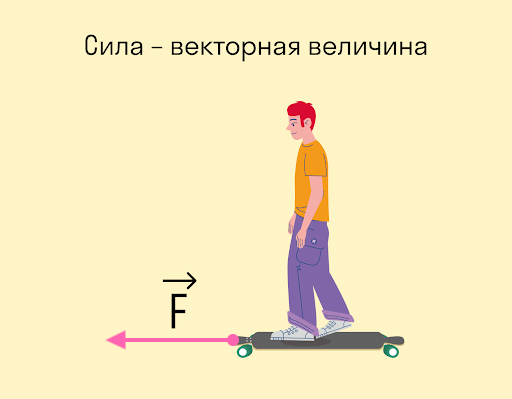
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Деформация
Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил
Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.
На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.
По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:
Сила упругости: Закон Гука
Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).
При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.
Какой буквой обозначается сила упругости?
Закон Гука
Fупр = kx
Fупр — сила упругости [Н]
k — коэффициент жесткости [Н/м]
х — изменение длины (деформация) [м]
Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.
Это равноценные обозначения — можно использовать любое удобное.
Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.
Задачка
На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?
Решение:
Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.
Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :
Тогда из Закона Гука выразим модуль удлинения лески:
Выражаем модуль удлинения:
Подставим числа, жесткость лески при этом выражаем в Ньютонах:
x=3/(0,3 * 1000)=0,01 м = 1 см
Ответ: удлинение лески равно 1 см.
Параллельное и последовательное соединение пружин
В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.
Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.
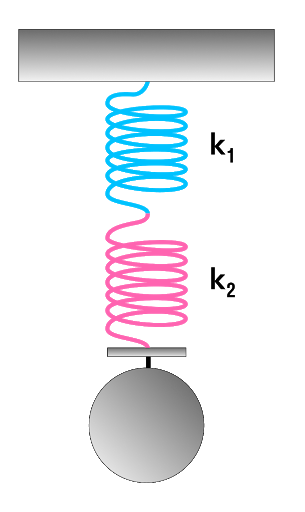
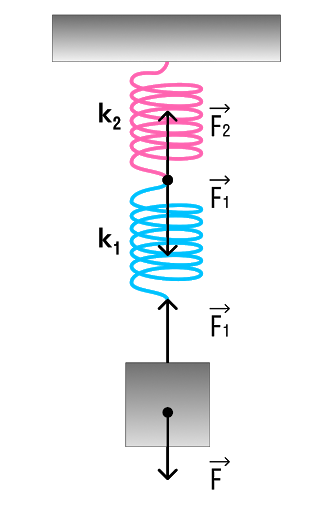
Последовательное соединение системы пружин
Последовательное соединение характерно наличием одной точки соединения пружин.
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
Коэффициент жесткости при последовательном соединении пружин
1/k = 1/k₁ + 1/k₂ + … + 1/k_i
k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
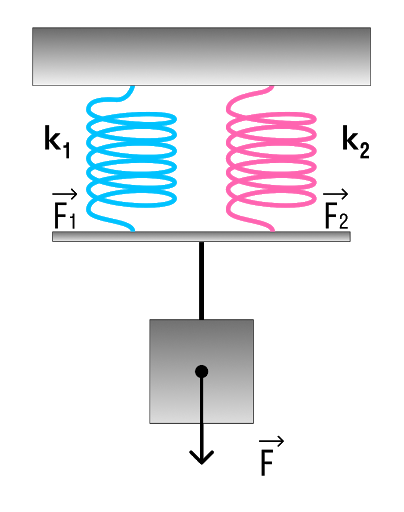
Параллельное соединение системы пружин
Последовательное соединение характерно наличием двух точек соединения пружин.
В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
Коэффициент жесткости при параллельном соединении пружин
k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
Задачка
Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?
Решение:
а) Рассмотрим параллельное соединение пружин.
При параллельном соединении пружин общая жесткость
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Рассмотрим последовательное соединение пружин.
При последовательном соединении общая жесткость двух пружин
1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015
k = 1000/15 = 200/3 ≃ 66,7 Н/м
График зависимости силы упругости от жесткости
Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
Задачка 1
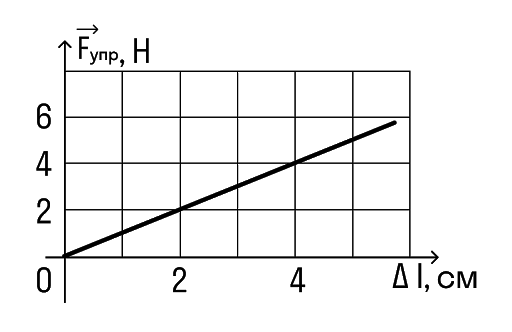
Определите по графику коэффициент жесткости тела.
Решение:
Из Закона Гука выразим коэффициент жесткости тела:
Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Например, возьмем вот эту точку.
В ней удлинение равно 2 см, а сила упругости 2 Н.
Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м
Ответ:жесткость пружины равна 100 Н/м
Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!
Задачка 2
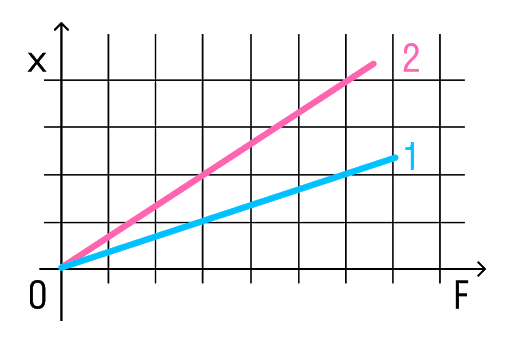
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.
Решение:
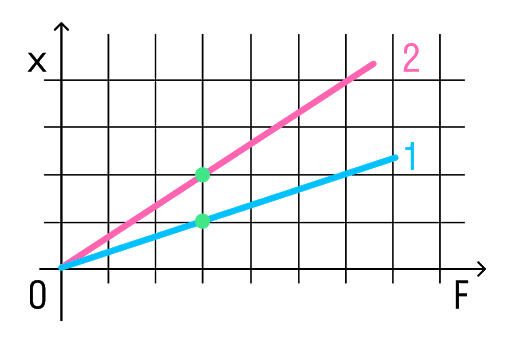
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.
Значит жесткость стальной проволоки больше.
Ответ: жесткость стальной проволоки больше медной.
Таблица формул для 7 класса
Копирование и распространение материалов сайта разрешается и очень приветствуется при наличии ссылки на сайт и автора.
Контакт
«Если у тебя есть яблоко, и у меня есть яблоко, и мы обменяемся этими яблоками, то у каждого из
нас так и будет одно яблоко. Если у тебя есть идея, и у меня есть идея, и мы обменяемся этими идеями,
то у каждого из нас будет по две идеи! «
Научная электронная библиотека
38. Треугольники и физика
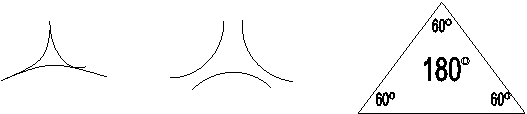
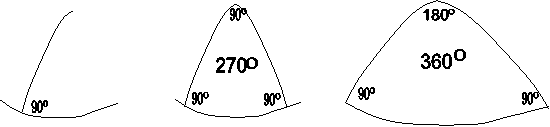
Но мир природы не создан человеком, а потому, какой он, неизвестно. Нужно выяснить, как он устроен, найти признаки строения природных объектов, по ним вывести понятия и, затем, законы функционирования природных явлений. Методология индуктивного и системного познания получила название ноотики.
Это евклидова геометрия, разработанная для замеров площадей фигур (полей, пастбищ) на земной поверхности. При этом поверхность Земли была принято плоской. Это нереальный мир природы.
Если принять, что геометрия разрабатывалась с целью изучения фигур на поверхности земного шара, то ни евклидова геометрия на плоской гладкой поверхности, ни риманова геометрия построения фигур на внутренней поверхности шара с отрицательной кривизной, не отражают реального мира рельефа каменной оболочки с положительной кривизной (выпуклые, а не вогнутые фигуры) и негладкой поверхностью. Но именно таким является мышление физиков (математический язык) при объяснениях природных объектов и явлений. Например, при создании общей теории относительности А. Эйнштейн учитывал представления Г.Ф. Римана о кривизне пространства. В четырехмерном римановском пространстве-времени общей теории относительности тензор кривизны имеет 20 компонентов.
Представления о пространстве на псевдосфере, изнутри шара, формируют воззрения о центре объектов: атома, Земли, Вселенной, развитии объектов от центров к периферии, их создании, начале.
Такая геометрия с выпуклыми фигурами (положительной кривизной) отражает реальный мир природы, называется сферической и используется астрономами. Пространство представляется бесконечным, а, потому, как система, не имеющая начала, не сотворено, а существует.
Что означает треугольник в физике перед буквой
| ◄ | ΐ | Α | Β | Γ | Δ | Ε | Ζ | Η | Θ | ► |
| ◄ | ΰ | α | β | γ | δ | ε | ζ | η | θ | ► |
δ: greek small letter delta
δ: U+03B4
Использование [ править | править код ]
Прописная буква Δ используется как символ для обозначения:
Строчная буква δ используется как символ для обозначения:
Также с греческой буквой сходны другие символы, употребляемые в математике:
Презентация к уроку
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Эпиграф:
Все науки настолько связаны между собой, что легче изучать их все сразу, нежели какую-либо одну из них в отдельности от всех. (Рене Декарт)
Цели урока:
Оборудование: мультимедийный проектор, карточки для самостоятельной работы по геометрии и физике.
Задачи учителей: показать практическое применение теоретических знаний по геометрии при решении задач по физике.
I. Вызов интереса
Задача индийского математика XII века Бхаскары.
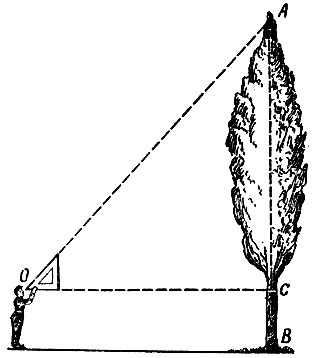
Учитель математики. Историческая справка. Первое представление о прямоугольном треугольнике греки получили, рассматривая верёвку, косо идущую от вершины шеста. Катетом они назвали вертикальный шест, а “гипотенузо” — означает “натянутое”.
Таким образом, можно было определить расстояние до недоступных предметов, например, высоту дерева.
Прямоугольный треугольник занимает почетное место в вавилонской геометрии, упоминание о нем встречается в папирусе Ахмеса.
Термин гипотенуза происходит от греческого hypoteinsa, означающего тянущаяся под чем-либо, стягивающая. Слово берет начало от образа древнегреческих арф, на которых струны натягивались на концы двух взаимно перпендикулярных подставок.
Термин катет происходит от греческого слова “катетос”, которое означало отвес,
перпендикуляр. Евклид употреблял выражения: “стороны, заключающие прямой угол” – для катетов; “сторона, стягивающая прямой угол” – для гипотенузы.
Небесные светила так же являются недоступными для точного измерения, а человеку всегда хотелось знать о том, каково расстояние между планетами. Как быть? На этот вопрос готова ответить математика.
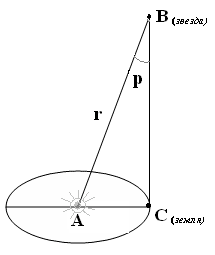
Параллакс (греч. “смена, чередование”) — изменение видимого положения объекта относительно удалённого фона в зависимости от положения наблюдателя. На сегодняшний день параллаксы всех планет и ближайших звезд измерены.
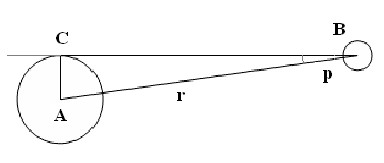
Параллакс определяют из двух точек земной поверхности, находящихся на одном географическом меридиане и имеющих известные географические широты.
Отрезок АС, длина которого тщательно измерена, называется базисом.
Угол АВС, под которым из недоступного места виден базис, называется параллаксом и обозначается – р.
При определении расстояний до тел солнечной системы в качестве базиса используют радиус Земли, т.е. АC = Rз = 6378 км.
r = АС : sin p = R : sin p = R : р = R х 206265″ : р (км)
При определении расстояний до ближайших звезд за базис принимают большую полуось земной орбиты, т.е. АС = 150 000 000 км = 1 а.е.
(1 астрономическая единица)
Параллакс – угол, под которым со звезды была бы видна большая полуось земной орбиты, развернутая перпендикулярно направлению на звезду.
Чем меньше параллакс, тем дальше находится звезда.
r = АС : sin р = 1 : sin р = 1 : р = 206265″ : р (а.е.)
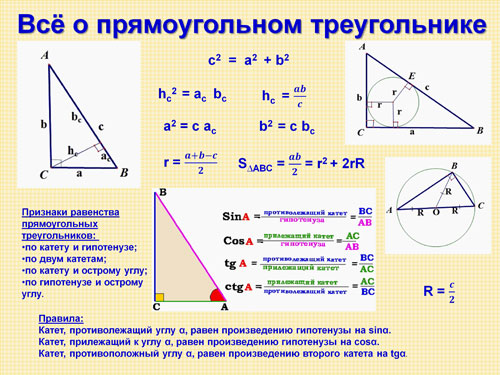
II. Повторение ранее изученного материала
Учитель математики. Каждый человек, заботящийся о своем здоровье, начинает день с зарядки. Вот и мы для начала проведем интеллектуальную разминку.
Я предлагаю вам в течение 4 минут вспомнить и записать все самое важное о прямоугольном треугольнике, что вы изучали на уроках геометрии.
Через заданное время учащиеся вместе с учителем обсуждают записанное. Если каких-либо данных не хватает, учитель обращает на это внимание. В итоге учащимся раздается подготовленная учителем таблица с основными данными о прямоугольном треугольнике.
III. Решение физических задач
1. С каким ускорением скользит брусок по наклонной плоскости высотой 60 см и длиной 1 м, если коэффициент трения равен 0,2?
2. Заряды по 0,1 мкКл расположены на расстоянии 6 см друг от друга. Найти напряженность поля в точке, удаленной на 5 см от каждого из зарядов.
3. На каком расстоянии от собирающей линзы с фокусным расстоянием 60 см следует поместить предмет, чтобы получить действительное изображение, увеличенное в 2 раза?
IV. Физкультминутка
V. Тестирование
Учащимся предлагаются два теста: часть учащихся садится за компьютеры и выполняет тест по физике. Оставшиеся учащиеся выполняют тест по математике за партами. Все задания в тестах взяты из реальных ЕГЭ.
Тест по математике
5. В прямоугольном треугольнике АВС с углом А равным 36° проведены медиана СМ и биссектриса CD. Найдите угол DCМ (в градусах)
Тест по физике
1. Найти проекцию вектора силы тяжести на ось ОХ.
2. Лодка должна попасть на противоположный берег по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки u, а скорость лодки относительно воды v. Чему равна скорость лодки относительно берега?
3. На каком расстоянии нужно поместить предмет перед собирающей линзой, чтобы получить действительное изображение на расстоянии 60 см от линзы? Высота изображения должна быть в 3 раза больше высоты предмета.
4. На рисунке дан ход лучей, полученный при прохождении света через плоскопараллельную пластинку. Чему равен показатель преломления вещества пластинки?
5. Туристы прошли 300 м на восток и, оказавшись перед болотом, повернули на север, пройдя 400 м. Чему равна длина перемещения и пройденный ими путь?
В данной статье поговорим о знаке Дельта — что он из себя представляет, в каких сферах применяется и для чего вообще используется. Также вы узнаете, как выглядит знак и как его можно вставить в текст в такой программе, какой является Ворд из Майкрософт Оффис.
Знак Дельта применяется во многих сферах жизнедеятельности, к примеру, в физике, текстовых редакторах, формулах и других сферах. Чаще всего именно при печати учебной литературы, докладов и других видов документов применяют знак дельта, который имеется в разных версиях ВОРД от Виндовс и других приложениях для создания документов текстового формата на ПК.
О происхождения знака
Буква, которая служит аналогом в русском алфавите – Д, а вот символ везде одинаков и изображается, как геометрическая фигура, а именно треугольник с равными сторонами (Δ). Эта версия является заглавной, прописная версия выглядит немного иначе, представляя собой кружок с хвостиком, похожий на обозначение в физике плотности (δ).
Где применяется данный символ?
Кроме использования в правописании греков, символ начали активно применять в математике, геометрии, алгебре, физике, химии и географии.
Поговорим отдельно о применении дельта в каждых научных сферах:
Как ввести в «Ворд»?
Треугольник. Формулы и свойства треугольников.
Типы треугольников
По величине углов
По числу равных сторон
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Связь между вписанной и описанной окружностями треугольника
Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника
Формула Герона
Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Подобие треугольников
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.