Что означает термин алгебра
Алгебра
А́лгебра (от араб. الجبر , «аль-джабр» — восполнение [1] ) — раздел математики, который можно грубо охарактеризовать как обобщение и расширение арифметики. Слово «алгебра» также употребляется в названиях различных алгебраических систем. В более широком смысле под алгеброй понимают раздел математики, посвящённый изучению операций над элементами множества произвольной природы, обобщающий обычные операции сложения и умножения чисел.
Алгебра — это наука, изучающая алгебраические системы с точностью до изоморфизма.
Алгебраическая система — упорядоченная пара множеств 
. Первое множество (
) — элементы какой либо природы (числа, понятия, буквы). Второе множество (
) — операции над первым множеством (сложение, умножение, возведение в степень). Примеры: группа, кольцо, поле.
Содержание
История
Истоки алгебры уходят к временам глубокой древности. Ещё 4000 лет назад вавилонские учёные могли решать квадратные уравнения. Тогда никаких обозначений не было, и уравнения записывались в словесной форме. Первые обозначения появились в Древней Греции благодаря учёному Диофанту. Неизвестное число он назвал «ἀριθμός», вторую степень неизвестного — «δύναμις», третью «κύβος», четвёртую — «дюнамодюнамис», пятую — «дюнамокюбос», шестую — «кюбоккюбос». Все эти величины он обозначал сокращениями (ар, дю, кю, ддю, дкю, ккю). Ни вавилоняне, ни греки не знали и не признавали отрицательные числа.
За 2000 лет до нашего времени китайские учёные решали уравнения первой степени и их системы, а также квадратные уравнения. Они уже знали отрицательные и иррациональные числа. Поскольку в китайском языке каждый символ обозначает понятие, то сокращений не было. В 13 веке китайцы открыли закон образования биномиальных коэффициентов, ныне известный как «треугольник Паскаля». В Европе он был открыт лишь 250 лет спустя. [2]
В 12 веке алгебра попала в Европу. С этого времени начинается её бурное развитие. Были открыты способы решения уравнений 3 и 4 степеней. Распространения получили отрицательные и комплексные числа. Было доказано, что любое уравнение выше 4 степени нельзя решить алгебраическим способом.
Вплоть до второй половины XX века практическое применение алгебры ограничивалось, в основном, решением алгебраических уравнений и систем уравнений с несколькими переменными. Во второй половине XX века началось бурное развитие ряда новых отраслей техники. Появились электронно-вычислительные машины, устройства для хранения, переработки и передачи информации, системы наблюдения типа радара. Проектирование новых видов техники и их использование немыслимо без применения современной алгебры. Так, электронно-вычислительные машины устроены по принципу конечных автоматов. Для проектирования электронно-вычислительных машин и электронных схем используются методы булевой алгебры. Современные языки программирования для ЭВМ основаны на принципах теории алгоритмов. Теория множеств используется в системах компьютерного поиска и хранения информации. Теория категорий используется в задачах распознавания образов, определении семантики языков программирования, и других практических задачах. Кодирование и декодирование информации производится методами теории групп. Теория рекуррентных последовательностей используется в работе радаров. Экономические расчеты невозможны без использования теории графов. Математическое моделирование широко использует все разделы алгебры.
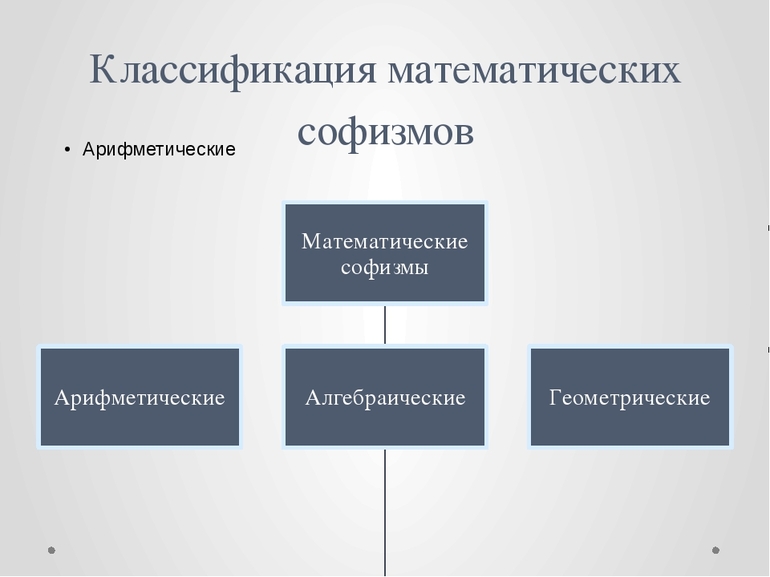
Классификация
Алгебру можно грубо разделить на следующие категории:
В некоторых напралениях углублённого изучения, аксиоматические алгебраические системы, такие как группы, кольца, поля и алгебры над полем на присутствие геометрических структур (метрик и топологий), совместимых с алгебраическими структурами. Список некоторых разделов функционального анализа:
Элементарная алгебра
Элементарная алгебра — раздел алгебры, который изучает самые базовые понятия. Обычно изучается после изучения основных понятий арифметики. В арифметике изучаются числа и простейшие (+, −, ×, ÷) действия с ними. В алгебре числа заменяются на переменные (a,b,c,x,y и так далее). Такой подход полезен, потому что:
Значение слова «алгебра»
[Лат. algebra из араб.]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
А’ЛГЕБРА, ы, мн. нет, ж. [от араб.]. Отдел математики, часть математического анализа (см. анализ).
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
а́лгебра
1. раздел математики, посвящённый изучению операций над элементами множества произвольной природы, обобщающих обычные операции сложения и умножения чисел
2. то же, что элементарная алгебра, раздел алгебры [1], охватывающий свойства операций с вещественными и комплексными числами, а также правила тождественных преобразований математических выражений и уравнений с использованием символов, обозначающих такие числа, и элементарных функций
3. тип алгебраических структур; множество из каких-либо объектов, над элементами которого определены некоторые операции, являющиеся, как правило, обобщением сложения и умножения
4. книжн. сложная система навыков, знаний, методов в какой-либо области ◆ Нужны объективные методы оценки эффективности производств, включающие в себя не только арифметику, но и социальную алгебру нашей действительности. Марина Наумова, «Рыба ищет где глубже», 2001 г. ◆ Очень грубый подсчёт показывает абсолютное преобладание тех, кто может выиграть от дерегулирования занятости. Почему тогда реформы в этой сфере остаются столь сложными с политической точки зрения? Почему аргумент от простой арифметики в их поддержку недостаточен, а необходима хитроумная алгебра политических комбинаций? Владимир Гимпельсон, «Пора дерегулировать?», 2003 г.
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: отвильнуть — это что-то нейтральное, положительное или отрицательное?
А́ЛГЕБРА
Том 1. Москва, 2005, стр. 415
Скопировать библиографическую ссылку:
А́ЛГЕБРА [ср.-век. лат. algebra, от араб. аль-джебр, аль-джабр – воссоединение (отдельных частей уравнения)], раздел математики, принадлежащий, наряду с арифметикой и геометрией, к числу старейших ветвей этой науки; она изучает операции над математич. объектами и влияет на формирование общих понятий и методов математики. Задачи и методы А. заключались первоначально в составлении и решении уравнений. В связи с исследованиями уравнений развивалось понятие числа, были введены отрицательные, рациональные, иррациональные и комплексные числа; общее исследование свойств этих числовых систем относится к А. В алгебре сформировались буквенные обозначения, позволившие записать свойства действий над числами в форме, не содержащей конкретных чисел. Преобразования по определённым правилам (связанным со свойствами действий) буквенных выражений составляет аппарат классич. А. Развитие А. оказало большое влияние на развитие новых областей математики, в частности математич. анализа, дифференциального и интегрального исчисления. Применение А. возможно всюду, где приходится иметь дело с операциями, аналогичными сложению и умножению чисел. Эти операции могут производиться над объектами самой различной природы. Наиболее известным примером такого расширенного применения алгебраич. методов является векторная алгебра (см. Линейная алгебра ) и её дальнейшее обобщение – тензорная алгебра (см. Тензорное исчисление ), ставшая одним из важных средств совр. физики.
Классификация раздела
Алгебра является разделом математики. Она классифицируется на несколько видов:
Каждый из этих разделов решает определенные задачи. При этом наука не стоит на месте и продолжает развитие.
Древняя история
Информация об истории возникновения алгебры связывается с древними рукописями. В те времена появилось понятие о натуральных числах, с которыми можно было проводить арифметические операции. Такая потребность возникла в связи с проведением астрономических и других видов расчетов. Изучая историю алгебры, становится понятно, что ее зарождение произошло в античной Греции.
Происхождение науки связывается с мыслителем Диофантом. На сегодняшний день трудно сказать, кто придумал алгебру, но именно этим человеком были впервые введены буквенные обозначения чисел. На основании полученных сообщений известно, что Диофант знал о сокращении чисел и умел переносить члены из разных частей уравнения.
Информация об ученом содержится только в одном историческом труде, поэтому сказать точно, что математик создал алгебру, невозможно. К тому же этот источник дошел до нынешних времен не в полном объеме.
Продвижение на Восток
Достижения европейцев в области развития алгебры прервались после нашествий варварских племен. Кроме того, уменьшение к ней интереса произошло с открытием геометрии, которая стала считаться основным разделом математики. В этот период многие науки получили свое развитие на Востоке. Здесь продолжилось становление и алгебры. Поскольку все достижения Европы практически были забыты, создателем этой науки в мусульманском мире считается Ала-Хорезми. Произошло это после создания им трактата под названием «Учение об отношениях, перестановках и решениях». Некоторые ученые считают, что слово «алгебра» может вести свое начало от термина «алгоритм».
При этом существуют гипотезы, что мусульманский мир опирался в своих изучениях на европейские достижения. В некоторых их летописях присутствуют фамилии греческих последователей Диофанта, приводятся их высказывания относительно этой науки.
Вклад других стран
Основателем алгебры считается Ала-Хорезми, но особого развития она у арабов она получила. Однако именно они изобрели на своем языке арабские цифры, которые применяются в современном мире. Существенный вклад в развитие науки внесли представители и других стран. Кратко их достижения выражаются в следующем:
Таким образом, в развитии этого раздела принимали участие многие страны мира. Их исследовательские работы вносили общий вклад в становление алгебры.
Под конец XVI века эта часть математики снова возвращается в Европу, откуда она взяла свое начало. Этому способствовало купечество, разъезжающее по всему свету и знакомившееся с математикой. Дальнейший толчок произошел после распада феодальной системы. Страны, ставшие на капиталистический путь развития, уже не могли обойтись без алгебраических действий.
Алгебра относится к наиболее интересным наукам, которые изучаются учениками школ и студентами вузов. Учащиеся постоянно пишут рефераты и готовят доклады на различные темы, относящиеся к этому разделу математики. В дальнейшем они зачитывают свои работы на уроках.
Значение слова алгебра
алгебра в словаре кроссвордиста
алгебра
Толковый словарь живого великорусского языка, Даль Владимир
ж. наука счисления буквами и другими условными знаками, взамен цифр, которые вставляются только при окончательном выводе; буквосчисление, общая арифметика. Алгебраический, алгебрический, к сему способу относящийся. Алгебраист, алгебрист м. сведущий в науке этой.
Толковый словарь русского языка. Д.Н. Ушаков
алгебры, мн. нет, ж. (от араб.). Отдел математики, часть математического анализа (см. анализ).
Толковый словарь русского языка. С.И.Ожегов, Н.Ю.Шведова.
-ы, ж. Раздел математики, изучающий такие качества величин к-рые вытекают из отношений между величинами и не зависят от их природы.
Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова.
Раздел математики, изучающий свойства переменных числовых величин и общих методов решения задач при помощи уравнений.
Учебный предмет, содержащий основы данного раздела математики.
разг. Учебник, излагающий содержание данного учебного предмета.
Энциклопедический словарь, 1998 г.
АЛГЕБРА (араб.) часть математики, развивающаяся в связи с задачей о решении алгебраических уравнений. Решение уравнений 1-й и 2-й степеней известно еще с древности. В 16 в. итальянскими математиками найдены решения уравнений 3-й и 4-й степеней. К. Гауссом установлено (1799), что всякое алгебраическое уравнение n-й степени имеет n корней (решений), действительных или мнимых. В нач. 19 в. Н. Абель и Э. Галуа доказали, что решения уравнений степени выше 4-й, вообще говоря, нельзя выразить через коэффициент уравнения при помощи алгебраических действий. В современной алгебре изучается общая теория совокупностей, в которых определены алгебраические операции, аналогичные по своим свойствам действиям над числами. Такие операции могут выполняться, напр., над многочленами, векторами, матрицами и т.д.
Имена, названия, словосочетания и фразы содержащие «алгебра»:
Большая Советская Энциклопедия
(По материалам статьи А.Г. Куроша и О. Ю. Шмидта из 2-го изд. БСЭ).
Современное состояние алгебры
Сфера приложений математики расширяется с течением времени, и темп этого расширения возрастает. Если в 18 в. математика стала основой механики и астрономии, то уже в 19 в. она стала необходимой для различных областей физики, а ныне математические методы проникают даже в такие, казалось бы далекие от математики области знания, как биология, лингвистика, социология и т.д. Каждая новая область приложений влечёт создание новых глав внутри самой математики. Эта тенденция привела к возникновению значительного числа отдельных математических дисциплин, различающихся по областям исследования (теория функций комплексного переменного, теория вероятностей, теория уравнений математической физики и т. д.; более новые ≈ теория информации, теория автоматического управления и т. д.). Несмотря на такую дифференциацию, математика остаётся единой наукой. Это единство сохраняется благодаря развитию и совершенствованию ряда общих, объединяющих идей и точек зрения. Тенденция к объединению лежит в существе математики как науки, пользующейся методом абстракции и, кроме того, часто стимулируется тем, что при исследовании задач, возникающих в различных областях знания, приходится пользоваться одним и тем же математическим аппаратом.
Её выводом является цепочка равенств: (а + b)2= (a + b)(а + b) = (a + b)a + (а + b) b = (a2 + ba) + (ab + b2) = a2 + (ba + ab)+ b2 = a2 + 2ab + b2. Для обоснования мы дважды пользуемся законом дистрибутивности :. с(а + b) = ca + cb (роль с играет а + b) и (a + b) с = ac + bc (роль с играют а и b), закон ассоциативности при сложении позволяет перегруппировать слагаемые, наконец используется закон коммутативности : ba = ab. Что представляют собой объекты, закодированные буквами а и b, остаётся безразличным; важно, чтобы они принадлежали системе объектов, в которой определены две операции ≈ сложение и умножение, удовлетворяющие перечисленным требованиям, касающимся свойств операций, а не объектов. Поэтому формула останется верной, если а и b обозначают векторы на плоскости или в пространстве, сложение принимается сперва как векторное сложение, потом как сложение чисел, умножение ≈ как скалярное умножение векторов. Вместо а и b можно подставить коммутирующие матрицы (т. е. такие, что ab = ba, что для матриц может не выполняться), операторы дифференцирования по двум независимым переменным и т. д.
Наиболее важными алгебраическими системами с одной операцией являются группы. Операция в группе ассоциативна [т. е. верно (a *b) *с = а * (b *с) при любых а, b, с из группы; звёздочкой * обозначена операция, которая в разных ситуациях может иметь разные названия] и однозначно обратима, т.е. для любых а и b из группы найдутся единственные х, у, такие, что а *х = b, у *а = b. Примерами групп могут служить: совокупность всех целых чисел относительно сложения, совокупность всех рациональных (целых и дробных) положительных чисел относительно умножения. В этих примерах операция (сложение в первом, умножение во втором) перестановочна. Такие группы называют абелевыми. Совокупности движений, совмещающих данную фигуру или тело с собой, образуют группу, если в качестве операции взять последовательное осуществление двух движений. Такие группы (группы симметрии фигуры) могут быть неабелевыми. Движения, совмещающие с собой атомную решётку кристалла, образуют т. н. федоровские группы, играющие основную роль в кристаллографии и через нее в физике твёрдого тела. Группы могут быть конечными (группы симметрии куба) и бесконечными (группы целых чисел по сложению), дискретными (тот же пример) и непрерывными (группа вращений сферы). Теория групп стала разветвленной, богатой содержанием математической теорией, имеющей обширную область приложений. Не менее богатой приложениями является линейная А., изучающая линейные пространства. Под этим названием понимаются алгебраические системы с двумя операциями ≈ сложением и умножением на числа (действительные или комплексные). Относительно сложения объекты (называемые векторами) образуют абелеву группу, операция умножения удовлетворяет естественным требованиям:
а (х + у) = ax + ау, (а + b) х = ax + bx, 1×x = х, a(bx) = ab(x);
О других алгебраических системах, указанных выше, см. соответствующие статьи и литературу при них.
Лит.: История алгебры. Выгодский М. Я., Арифметика и алгебра в древнем мире, 2 изд., М., 1967; Юшкевич А. П., История математики в средние века, М., 1961; Вилейтнер Г., История математики от Декарта до середины XIX столетия, пер. с нем., 2 изд., М., 1966.
Классики науки. Декарт P., Геометрия, пер. с латин., М. ≈ Л., 1938; Ньютон И., Всеобщая арифметика, или книга об арифметических синтезе и анализе, пер. с лат., М., 1948; Эйлер Л., Универсальная арифметика, пер. с нем., т. 1 ≈ 2, СПБ. 1768 ≈ 69; Лобачевский Н. И., Полное собрание сочинений, т. 4 ≈ Сочинения по алгебре, М. ≈ Л., 1948: Галуа Э., Сочинения, пер. с франц., М. ≈ Л., 1936.
Монографии по общим вопросам алгебры. Ван-дер-Варден Б. Л., Современная алгебра, пер. с нем., 2 изд., ч. 1 ≈ 2, М. ≈ Л., 1947; Бурбаки Н., Алгебра, пер. с франц., [гл. 1 ≈ 9], М., 1962 ≈ 66; Курош А. Г., Лекции по общей алгебре, М., 1962.
Монографии по специальным разделам алгебры. Шмидт О., Абстрактная теория групп, 2 изд., М. ≈ Л., 1933; Курош А. Г., Теория групп, 3 изд., М., 1967; Понтрягин Л. С., Непрерывные группы, 2 изд., М., 1954; Чеботарев Н. Г., Основы теории Галуа, ч. 1 ≈ 2, М. ≈ Л., 1934 ≈ 37; Джекобсон Н., Теория колец, пер. с англ., М., 1947.