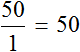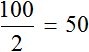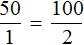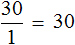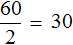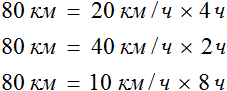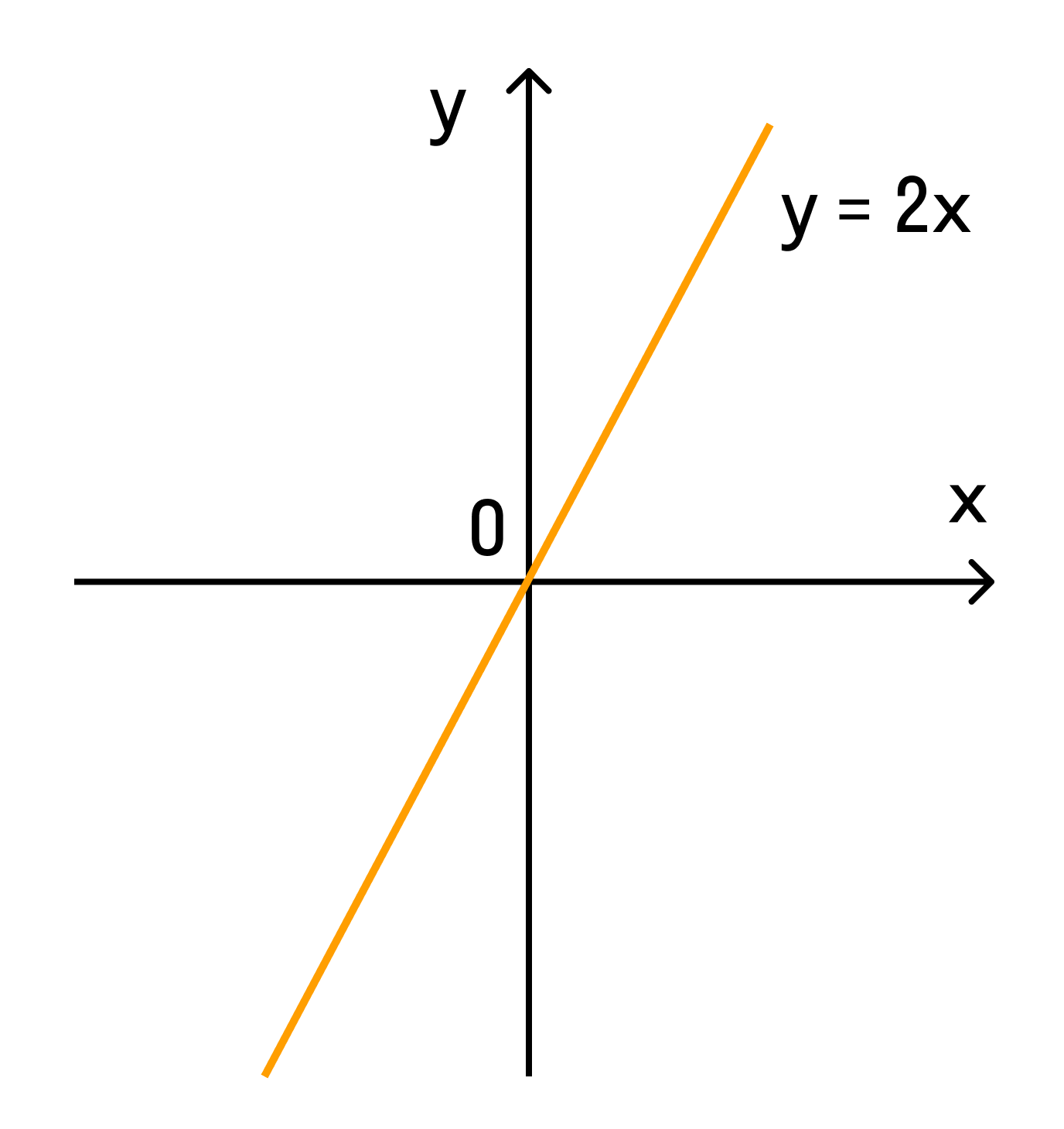Что означает стороны пропорциональны
Пропорциональные отрезки

Всего получено оценок: 313.
Всего получено оценок: 313.
Пропорциональные отрезки очень важны для определения подобия фигур. К тому же, правильно нареченные пропорционально рисунки помогают в правильном решении математических задач. Именно поэтому так важно разбираться в данной тематике.
Определение
Пропорциональными отрезками называются отрезки, у которых имеется постоянный коэффициент пропорциональности. Под коэффициентом пропорциональности понимается отношение длин отрезков.

Согласно определению пропорциональных отрезков, два отрезка всегда пропорциональны между собой, поскольку их длины не меняются со временем. Значит, не меняется и коэффициент пропорциональности.
Несмотря на это, чаще всего под пропорциональными отрезками понимают отрезки с коэффициентом кратным 0,5. Например, отрезки с коэффициентом 2,5, 1,5, 2 и тому подобные.
Пропорциональными будут являться и отрезки, составляющие подобные фигуры. Это действует в обе стороны. Если фигуры подобны, то их стороны пропорциональны, если все стороны пропорциональны, то фигуры подобны.
Подобные фигуры
Нужно понимать, что подобными фигурами могут быть не только треугольники, но вообще любые фигуры в геометрии, если все углы этих фигур равны, а длины сторон пропорциональны.

Но при этом признаки подобия существуют только для треугольников. Их всего 3:
Пропорциональными могут быть только отрезки, как объекты имеющие длину. Прямая или луч бесконечны, а потому не могут быть подобными.
Пример
Решим небольшую задачу на пропорциональность отрезков. Имеется 3 пропорциональных отрезка. Каждый из которых больше предыдущего. Первый отрезок равен 5, третий 20. Необходимо найти длину второго отрезка.
Отрезки пропорциональны, значит отношение больших к меньшим будет постоянным. Обозначим неизвестны отрезок за х и решим уравнение.
Перенесем выражение из правой части в левую. Приведем получившееся выражение под один знаменатель и решим дробно-рациональное уравнение.
Что мы узнали?
Мы узнали, что такое пропорциональные отрезки. Выделили области, где могут быть применены навыки обращения с пропорциональными длинами и привели пример на заданную тему.
Прямая и обратная пропорциональность
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз.
Пропорциональность бывает прямой и обратной. В данном уроке мы рассмотрим каждую из них.
Прямая пропорциональность
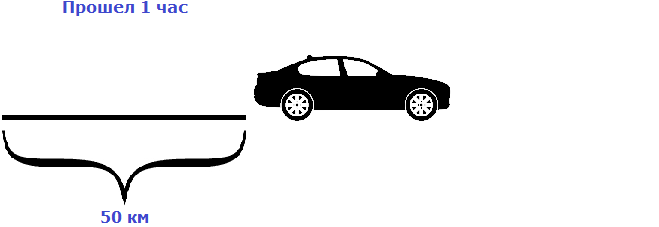
Предположим, что автомобиль двигается со скоростью 50 км/ч. Мы помним, что скорость это расстояние, пройденное за единицу времени (1 час, 1 минуту или 1 секунду). В нашем примере автомобиль двигается со скоростью 50 км/ч, то есть за один час он будет проезжать расстояние, равное пятидесяти километрам.
Изобразим на рисунке расстояние, пройденное автомобилем за 1 час
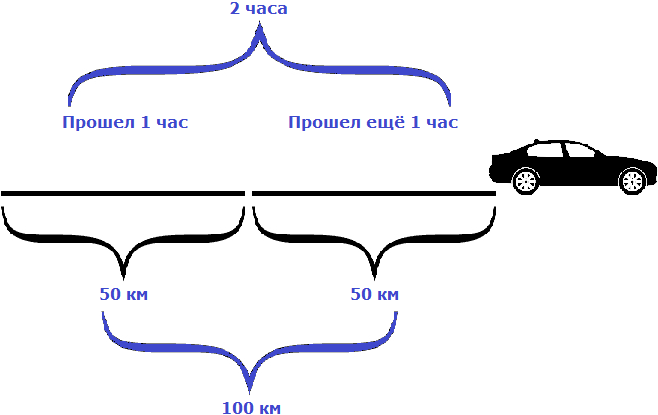
Пусть автомобиль проехал еще один час с той же скоростью, равной пятидесяти километрам в час. Тогда получится, что автомобиль проедет 100 км
Как видно из примера, увеличение времени в два раза привело к увеличению пройденного расстояния во столько же раз, то есть в два раза.
Такие величины, как время и расстояние называют прямо пропорциональными. А взаимосвязь между такими величинами называют прямой пропорциональностью.
Прямой пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.
и наоборот, если одна величина уменьшается в определенное число раз, то другая уменьшается во столько же раз.
Предположим, что изначально планировалось проехать на автомобиле 100 км за 2 часа, но проехав 50 км, водитель решил отдохнуть. Тогда получится, что уменьшив расстояние в два раза, время уменьшится во столько же раз. Другими словами, уменьшение пройденного расстояния приведет к уменьшению времени во столько же раз.
Интересная особенность прямо пропорциональных величин заключается в том, что их отношение всегда постоянно. То есть при изменении значений прямо пропорциональных величин, их отношение остается неизменным.
В рассмотренном примере расстояние сначала было равно 50 км, а время одному часу. Отношение расстояния ко времени есть число 50.
Но мы увеличили время движения в 2 раза, сделав его равным двум часам. В результате пройденное расстояние увеличилось во столько же раза, то есть стало равно 100 км. Отношение ста километров к двум часам опять же есть число 50
Число 50 называют коэффициентом прямой пропорциональности. Он показывает сколько расстояния приходится на час движения. В данном случае коэффициент играет роль скорости движения, поскольку скорость это отношение пройденного расстояния ко времени.
Из прямо пропорциональных величин можно составлять пропорции. К примеру, отношения 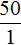
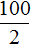
Это отношение можно прочитать следующим образом:
Пятьдесят километров так относятся к одному часу, как сто километров относятся к двум часам.
Пример 2. Стоимость и количество купленного товара являются прямо пропорциональными величинами. Если 1 кг конфет стоит 30 рублей, то 2 кг этих же конфет обойдутся в 60 рублей, 3 кг в 90 рублей. С увеличением стоимости купленного товара, его количество увеличивается во столько же раз.
Поскольку стоимость товара и его количество являются прямо пропорциональными величинами, то их отношение всегда постоянно.
Запишем чему равно отношение тридцати рублей к одному килограмму
Теперь запишем чему равно отношение шестидесяти рублей к двум килограммам. Это отношение опять же будет равно тридцати:
Здесь коэффициентом прямой пропорциональности является число 30. Этот коэффициент показывает сколько рублей приходится на килограмм конфет. В данном примере коэффициент играет роль цены одного килограмма товара, поскольку цена это отношение стоимости товара на его количество.
Обратная пропорциональность
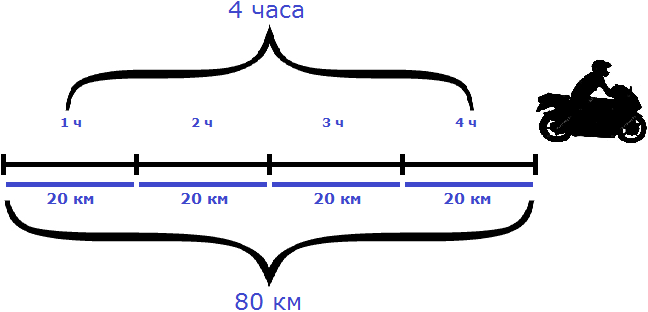
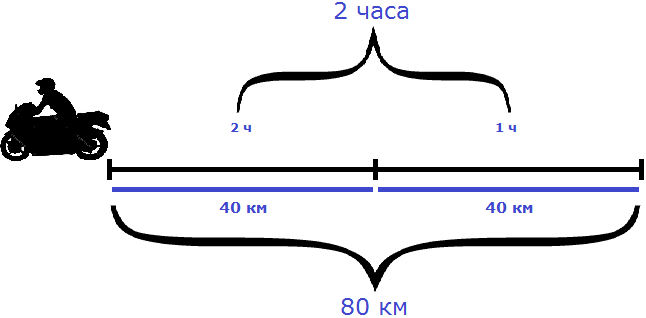
Рассмотрим следующий пример. Расстояние между двумя городами 80 км. Мотоциклист выехал из первого города, и со скоростью 20 км/ч доехал до второго города за 4 часа.
Если скорость мотоциклиста составила 20 км/ч это значит, что каждый час он проезжал расстояние равное двадцати километрам. Изобразим на рисунке расстояние, пройденное мотоциклистом, и время его движения:
На обратном пути скорость мотоциклиста была 40 км/ч, и на тот же путь он затратил 2 часа.
Легко заметить, что при изменении скорости, время движения изменилось во столько же раз. Причем изменилось в обратную сторону — то есть скорость увеличилась, а время наоборот уменьшилось.
Такие величины, как скорость и время называют обратно пропорциональными. А взаимосвязь между такими величинами называют обратной пропорциональностью.
Обратной пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой уменьшение другой во столько же раз.
и наоборот, если одна величина уменьшается в определенное число раз, то другая увеличивается во столько же раз.
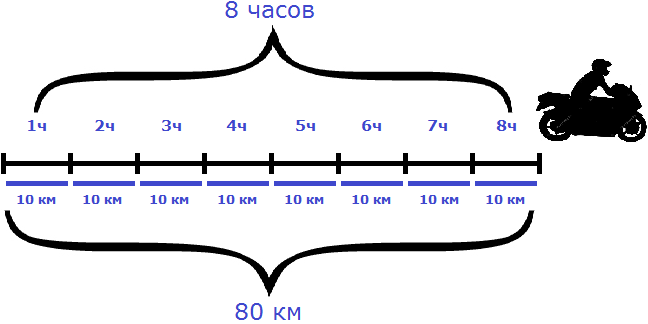
К примеру, если на обратном пути скорость мотоциклиста составила бы 10 км/ч, то те же 80 км он преодолел бы за 8 часов:
Как видно из примера, уменьшение скорости привело к увеличению времени движения во столько же раз.
Особенность обратно пропорциональных величин заключается в том, что их произведение всегда постоянно. То есть при изменении значений обратно пропорциональных величин, их произведение остается неизменным.
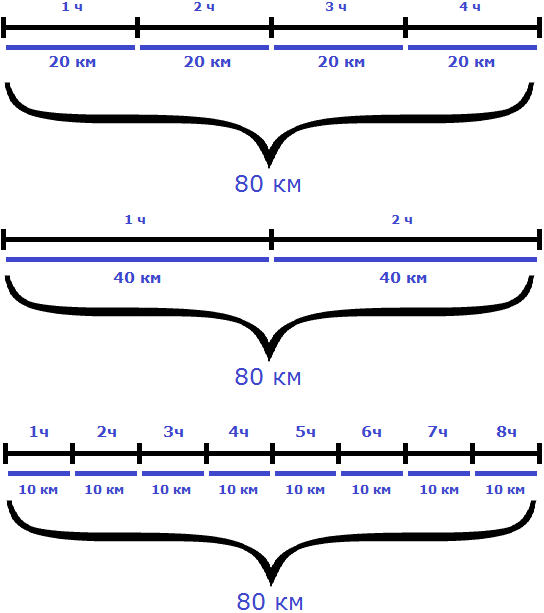
В рассмотренном примере расстояние между городами было равно 80 км. При изменении скорости и времени движения мотоциклиста, это расстояние всегда оставалось неизменным
Мотоциклист мог проехать это расстояние со скоростью 20 км/ч за 4 часа, и со скоростью 40 км/ч за 2 часа, и со скоростью 10 км/ч за 8 часов. Во всех случаях произведение скорости и времени было равно 80 км
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
10 thoughts on “Прямая и обратная пропорциональность”
что ценно теория методически верно преподается. очень добрый сайт.
мне теперь всё понятно, большое спасибо сайту
Прямая и обратная пропорциональность
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.
Зависимости также можно классифицировать по формам: функциональная и статистическая.
Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное и единственное значение другой.
В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y = f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.
Статистическая зависимость — это зависимость случайных величин, когда изменение одной переменной приводит к изменению другой.
Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.
Есть две разновидности пропорциональностей:
Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.
Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».
Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.
Формула прямой пропорциональности
y = kx,
где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Графиком прямо пропорциональной зависимости величин является прямая линия.
Например, при k = 2 график выглядит так:
Пример 1.
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.
Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:
Ответ: 20 человек напишут 420 постов за 12 дней.
Обратно пропорциональные величины
Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.
Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».
Свойство обратной пропорциональности величин:
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Примеры обратно пропорциональной зависимости:
Формула обратной пропорциональности
где y и x — это переменные величины,
k — постоянная величина, которую называют коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
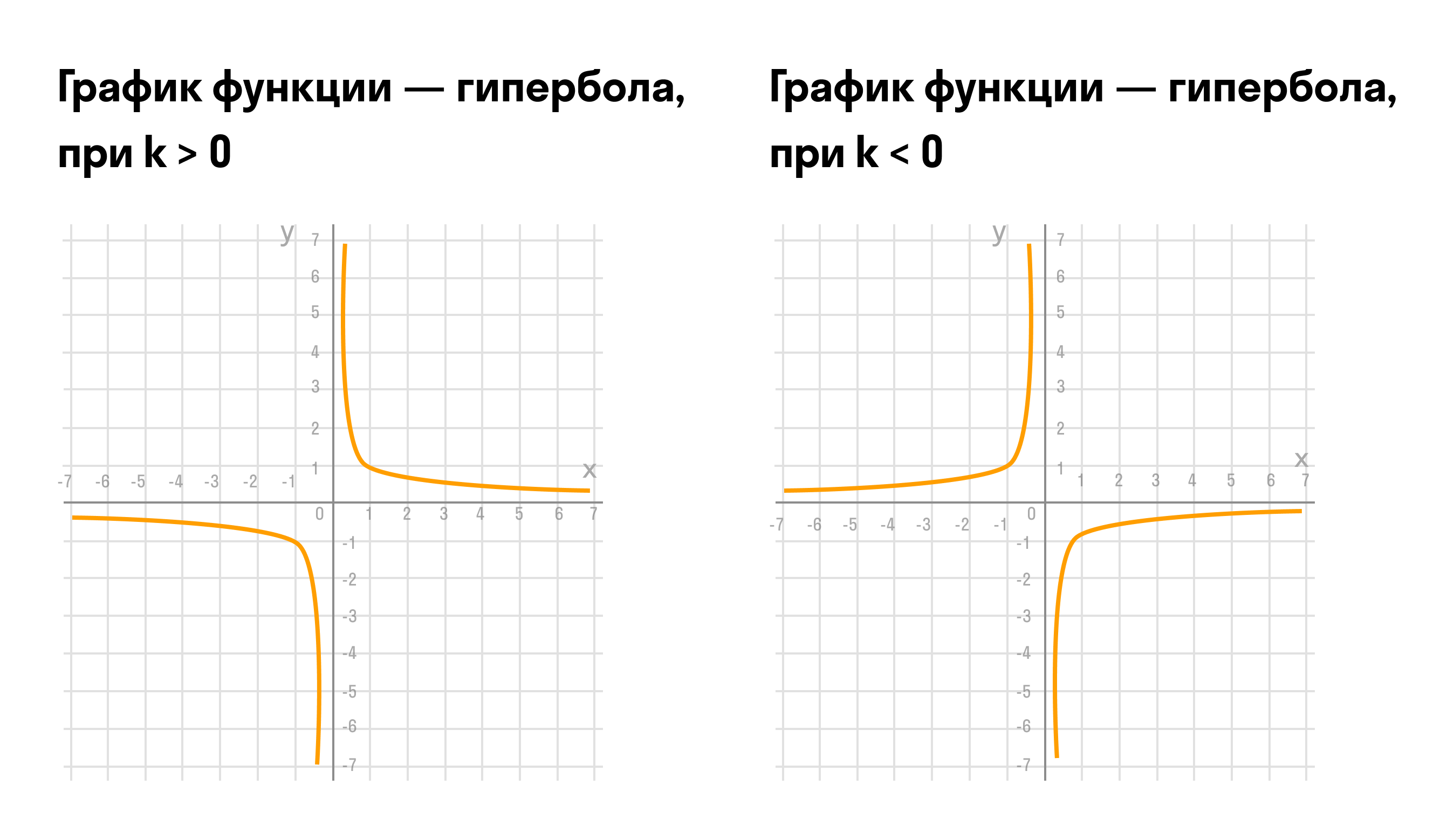
Графиком обратно пропорциональной зависимости величин является гипербола.
Свойства функции обратной пропорциональности:
Потренируемся
Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
Соотношения равны, но перевернуты относительно друг друга.
Что такое пропорция
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое пропорция
Пропорция — это равенство двух отношения.
Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.
Пропорция всегда содержит равные коэффициенты.
Если выразить определение формулой, то выглядеть оно будет так:
a и d — крайние члены пропорции
Читается это выражение так: a так относится к b, как c относится к d
Например:
Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.
15 и 3 — крайние члены пропорции.
5 и 9 — средние члены пропорции.
Наглядный пример для понимания:
У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.
Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!
А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.
Что мы имеем: 4 кусочка и 2 друга, претендующих на них.
Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.
Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.
Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным😉
Основное свойство пропорции
Запомните основное свойство пропорции:
Произведение крайних членов пропорции равно произведению средних членов этой пропорции.
В виде формулы свойство выглядит так:
a : b = c : d = a * d = b * c
Мы знаем, что a и d — крайние члены пропорции, b и c — средние.
Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.
Давайте проверим несколько пропорций.
Пример 1. Дана пропорция:6/2 = 12/4
Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.
Пример 2. Дана пропорция: 10/2 = 16/4
Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Примеры решения задач с пропорцией
Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек.
Задачка 1. Дана математическая пропорция: 15/3 = x/4
Ответ: в пропорции 15/3 = x/4, x = 20
Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.
Ответ: четвертый член пропорции — 12.
Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?
Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши.
Задачка 4. Дана пропорция: 20/2 = y/4
Значение слова «пропорциональный»
1. Обладающий пропорцией, находящийся в соразмерном соотношении частей. Пропорциональное сложение. □ [У Пушкина] было небольшое лицо и прекрасная, пропорциональная лицу, голова, с негустыми, кудрявыми волосами. И. Гончаров, Воспоминания. || Осуществляющийся с соблюдением пропорции, соразмерного соотношения частей. Пропорциональное развитие народного хозяйства. Пропорциональное распределение.
2. Находящийся в соответствующей зависимости от чего-л. Генерал жил во втором этаже и занимал помещение по возможности скромное, хотя и пропорциональное своему значению. Достоевский, Идиот.
3. Мат. Такой, который с увеличением или уменьшением одной из величин изменяется во столько же раз, находящийся в соотносительной количественной зависимости. Прямо пропорциональные величины. Обратно пропорциональные величины. □ Вычисления показали, что эта энергия [ветра] прямо пропорциональна высоте волн. Шулейкин, Дни прожитые.
[От лат. proportionalis — соразмерный]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Пропорциональные (между собой) величины. Прямо пропорциональные (см. прямой в 9 знач.), обратно пропорциональные (см. обратный в 4 знач.) величины. Пропорциональное деление (деление данной величины на части, пропорциональные заданным числам). Пропорционально (нареч.) чему-н. увеличиваться, уменьшаться. Длина окружности пропорциональна ее радиусу. || Находящийся в определенных соотношениях, в определенном количественном соответствии с чем-н. Пропорциональное обложение, п. налог (обложение всех доходов в одинаковом проценте, независимо от их величины, в противоп. прогрессивному; экон.). Пропорциональное представительство, пропорциональные выборы, пропорциональная избирательная система (система, при к-рой голосуют за списки, и количество избранных из списка соответствует количеству поданных за список голосов; полит.). П. циркуль (циркуль, употр. при увеличении или уменьшении чертежей в определенном масштабе; спец.).
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
пропорциона́льный
1. обладающий правильными пропорциями; соразмерный ◆ Старичок был весь чистота и благообразие: на лице его не было ни желтых пятен, ни морщин, обыкновенно портящих лица карликов; у него была очень пропорциональная фигурка, круглая как шар головка, покрытая совершенно белыми, коротко остриженными волосами, и небольшие коричневые медвежьи глазки. Н. С. Лесков, «Старые годы в селе Плодомасове», 1862 г. ◆ У него были большие загорелые руки, пропорциональные росту, с широкими ногтями. И. А. Гончаров, «Обрыв», 1869 г. ◆ Очевидно, что затрата сил должна быть пропорциональна трудности задачи〈…〉 Н. Я. Данилевский, «Россия и Европа», 1869 г. (цитата из НКРЯ)
2. осуществляющийся с соблюдением пропорции, соразмерного соотношения частей ◆ Всё, что было свежего, делилось пропорциональными частями, и опять ни одной жалобы и ни одного упрёка. Г. И. Невельской, «Подвиги русских морских офицеров на крайнем Востоке России», 1878 г. (цитата из НКРЯ) ◆ Горизонтальное бюджетное уравнивание подразумевает пропорциональное распределение налогов между субъектами федерации для нивелирования неравенства налоговых возможностей разных территорий. Т. Маглакелидзе, «Необходимость регулирования межбюджетных отношений в переходной экономике» (2003) // «Финансы и кредит», 15 мая 2003 г. (цитата из НКРЯ)
3. находящийся в определённом количественном соотношении с чем-либо ◆ Становясь на эту обобщающую точку зрения, мы не можем поэтому согласиться с коллективистами и не можем признать, чтобы вознаграждение, пропорциональное числу часов, употребленных каждым на производство этих богатств, представляло собою идеал или хотя бы шаг вперед по направлению к идеалу. П. А. Кропоткин, «Хлеб и воля», 1892 г. (цитата из НКРЯ) ◆ Применение пропорциональной системы, господствовавшей до 1993 года, при распределении депутатских мандатов на парламентских выборах вело к широкому представительству многих партий в обеих палатах парламента. Ж. М. Елубаева, «Система распределения доходных источников в Итальянской республике» (2003) // «Финансы и кредит», 19 мая 2003 г. (цитата из НКРЯ)
4. матем. такой, который с увеличением или уменьшением одной из величин изменяется во столько же раз, находящийся в соотносительной количественной зависимости ◆ Вообще, многоугольники называются подобные, когда в них все бока пропорциональны, все углы равны, притом бока следуют в том же порядке, в каком равные углы. Н. И. Лобачевский, «Новые начала Геометрии с полной теорией параллельных», 1835–1838 г. (цитата из НКРЯ) ◆ Лодж полагает, что количество пара, образующегося в каждый данный промежуток времени, не имеет надобности быть прямо пропорциональным количеству поглощаемого тепла и что, следовательно, вещество может перегреваться. А. М. Бутлеров, «Теоретические и экспериментальные работы по химии», 1851–1886 г. (цитата из НКРЯ)
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова спутываться (глагол), спутывались: