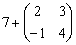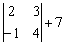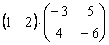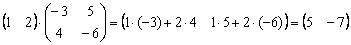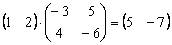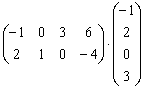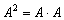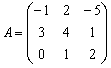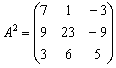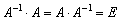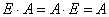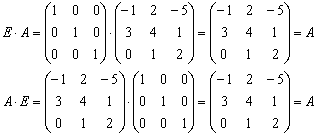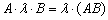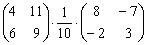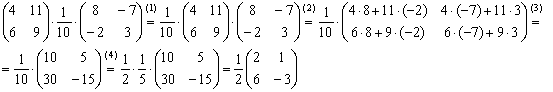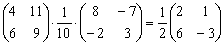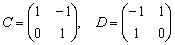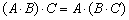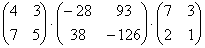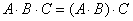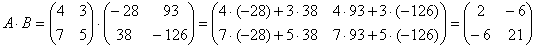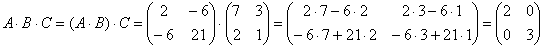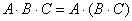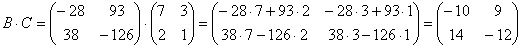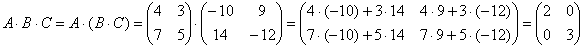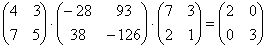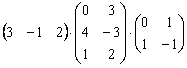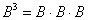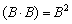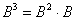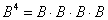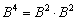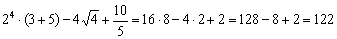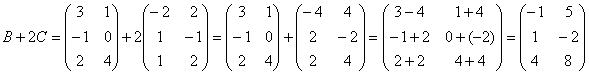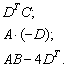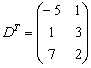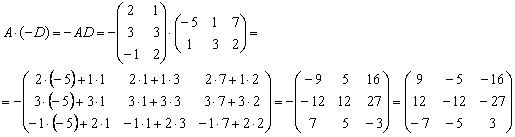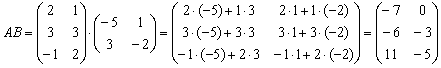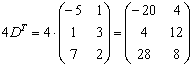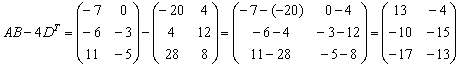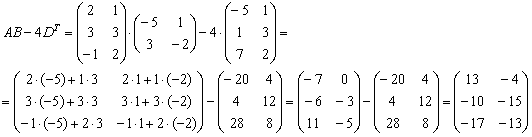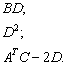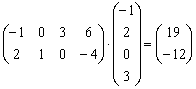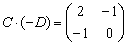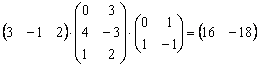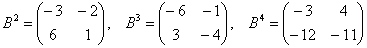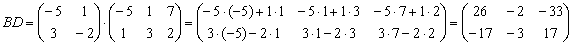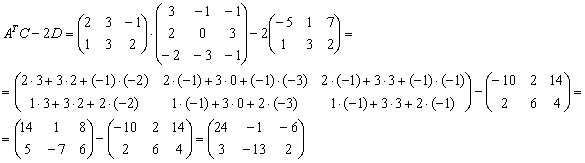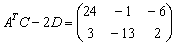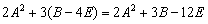Что означает степень т в матрице

Решение матриц методы решений и примеров для чайников, формулы вычислений и действий с матрицами

В высшей математике существует понятие матрицы системы чисел. С комбинацией элементов, заключённых в таблице, выполняют различные операции. Прежде чем переходить к решению матриц сложными методами, следует ознакомиться с понятием этого выражения и простейшими логическими операциями над ним.

Понятие выражения

Определение гласит, что матрица — это прямоугольная таблица с заключёнными в ней числами. Её название обозначается латинскими прописными буквами (А, В). Таблицы бывают разной размерности — прямоугольной, квадратной, а также в виде строк и столбцов.

От количества строк и столбцов будет зависеть величина таблицы. Матрица размера m*n означает, что в таблице содержится m строк и n столбцов. Допустим, первая строка включает элементы а11, а12, а13, вторая — а21, а22, а23. Тогда элементы, где i = j (а11, а22) образовывают диагональ и называются диагональными.

Различают комплексные матрицы, у которых хотя бы один элемент равен комплексному числу, и действительные, когда все её элементы являются действительными числами. В математике комплексные числа представлены в виде a+b*i, где:

На приведенном примере показаны варианты.

Простейшие действия с матрицами могут быть разными. К их числу относятся:

Сложение и вычитание

Действия по сложению возможны только тогда, когда матрицы одинакового порядка равны между собой. В итоге получится новое матричное выражение такой же размерности. Сложение и вычитание выполняются по общей схеме — над соответствующими элементами таблиц проводят необходимые операции. Например, нужно сложить две матрицы А и В размерности 2*2.

Каждый элемент первой строки складывается по порядку с показателями верхней строчки второй матрицы. По аналогии производится вычитание, только вместо плюса ставится минус.

Умножение на число

Любую таблицу чисел можно умножить на число. Тогда каждый её элемент перемножается с этим показателем. К примеру, умножим матричное выражение на 2:

Операция перемножения

Матрицы подлежат перемножению одна на другую, когда количество столбцов первой таблицы равно числу строк второй. Каждый элемент Aij будет равняться сумме произведений элементов i-строки первой таблицы, перемноженных на числа в j-столбце второй. Способ произведения наглядно представлен на примере.

Возведение в степень

Формулу возведения в степень применяют только для квадратных матричных выражений. При этом степень должна быть натуральной. Формула возведения следующая:

Иначе, чтобы выполнить операцию возведения таблицы чисел в степень n, требуется умножить её на себя саму n раз. Для операции возведения в степень удобно применять свойство в соответствии с формулой:

Решение представлено на примере. 1 этап: необходимо возвести в степень, где n = 2.

2 этап: сначала возводят в степень n =2. Согласно формуле перемножают таблицу чисел саму на себя n = 2 раз.

3 этап: в итоге получаем:

Расчёт определителя

В линейной алгебре существует понятие определителя или детерминанта. Это число, которое ставят в соответствие каждой квадратной матрице, вычисленное из её элементов по специальной формуле. Определитель или модуль используется для решения большинства задач. Детерминант самой простой матрицы определяется с помощью вычитания перемноженных элементов из побочной диагонали и главной.

Определителем матрицы А n-энного порядка называется число, которое получают из алгебраической суммы n! слагаемых, попадающих под определённые критерии. Эти слагаемые являются произведением n-элементов, взятых единично из всех столбов и строк.

Произведения могут отличаться друг от друга составом элементов. Со знаком плюс будут включаться в сумму числа, если их индексы составляют чётную подстановку, в противоположном случае их значение меняется на минус. Определитель обозначается символом det A. Круглые скобки матричной таблицы, обрамляющие её элементы, заменяются на квадратные. Формула определителя:

Определитель первого порядка, состоящий из одного элемента, равен самому этому элементу. Детерминант матричной таблицы размером 2*2 второго порядка вычисляется путём перемножения её элементов, расположенных на главной диагонали, и вычитания из них произведения элементов, находящихся в побочной диагонали. Наглядный пример:

Для матрицы также можно найти дискриминант многочлена, отвечающий формуле:

Когда у многочлена имеются кратные корни, тогда дискриминант равен нулю.

Обратная матрица

Прежде чем переходить к понятию обратного выражения матрицы, следует рассмотреть алгоритм её транспонирования. Во время операции строки и столбцы переставляются местами. На рисунке представлен метод решения:

По аналогии обратная матрица сходна с обратными числами. Например, противоположной цифре 5 будет дробь 1/5 = 5 (-1) степени. Произведение этих чисел равно 1, выглядит оно так: 5*5 (-1) = 1. Умножение обычной матричной таблицы на обратную даст в итоге единичную: А* А (-1) = Е. Это аналог числовой единицы.

Но для начала нужно понять алгоритм вычисления обратной матрицы. Для этого находят её определитель. Разработано два метода решения: с помощью элементарных преобразований или алгебраических дополнений.

Более простой способ решения — путём алгебраических дополнений. Рассмотрим матричную таблицу А, обратная ей А (-1) степени находится по формуле:

Матрица обратного вида возможна только для квадратного размера таблиц 2*2, 3*3 и т. д. Обозначается она надстроенным индексом (-1). Задачу легче рассмотреть на более простом примере, когда размер таблицы равен 2*2. На первом этапе выполняют действия:

2 этап: рассчитывают матрицу миноров, которая имеет те же значения, что и первоначальная. Под минором k-того порядка понимается определитель квадратной матрицы порядка k*k, составленный из её элементов, которые располагаются в выбранных k- столбцах и k-строках.

При этом расположение элементов таблицы не меняется. Чтобы найти минор верхнего левого числа, вычёркивают строчку и столбец, в которых прописан этот элемент. Оставшееся число и будет являться минором. На выходе должна получиться таблица:

3 этап: находят алгебраические дополнения.

4 этап: определяют транспонированную матрицу.

Проверка решения: чтобы удостовериться, что обратная таблица чисел найдена верно, следует выполнить проверочную операцию.

В рассматриваемом примере получается единичная матрица, когда на главной диагонали находятся единицы, при этом другие элементы равняются нулю. Это говорит о том, что решение было найдено правильно.

Нахождение собственных векторов

Определение собственного вектора и значений матричного выражения легче понять на примере. Для этого задают матричную таблицу чисел и ненулевой вектор Х, называемый собственным для А. Пример выражения:

Согласно теореме собственными числами матричного выражения будут корни характеристического уравнения:

Из однородной системы уравнений можно определить координаты собственного вектора Х, который соответствует значению лямбда.

Метод Гаусса

Методом Гаусса называют способ преобразования системы уравнений линейного вида к упрощённой форме для дальнейшего облегчённого решения. Операции упрощения уравнений выполняют с помощью эквивалентных преобразований. К таким относят:

Чтобы понять механизм решения, следует рассмотреть линейную систему уравнений.

Следует переписать эту систему в матричный вид:

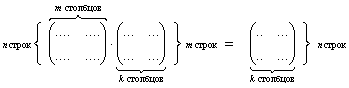
А будет являться таблицей коэффициентов системы, b — это правая часть ограничений, а Х — вектор переменных координат, который требуется найти. Для решения используют ранг матрицы. Под ним понимают наивысший порядок минора, который отличается от 0.

В этом примере rang (A) = p. Способ эквивалентных преобразований не изменяет ранг таблицы коэффициентов.

Метод Гаусса предназначен для приведения матричной таблицы коэффициентов А к ступенчатому или диагональному виду. Расширенная система выглядит так:

Обращают внимание на последние строки.

В этом случае система уравнений имеет решение, но когда хотя бы одно из этих чисел отличается от нуля, она несовместима. Таким образом, система совместима, если ранг таблицы А равен расширенному рангу В (А|b).

Если rang А=rang (A|b), то существует множество решений, где n-p — многообразие. Из этого следует n-p неизвестных Хр+1,…Xn выбираются произвольно. Неизвестные X1, X2,…Xp вычисляют следующим образом: из последнего уравнения выражают Хр через остальные переменные, вставляя в предыдущие выражения. Затем из предпоследнего уравнения получают Хр-1 через прочие переменные и подставляют их в предыдущие выражения. Процедуру повторяют.

Найти быстро ответ и проверить себя позволяет онлайн-калькулятор. Решение матрицы методом Гаусса с помощью такого расчёта показывает подробные этапы операций. Для нахождения достаточно указать количество переменных и уравнений, отметить в полях значения чисел и нажать кнопку «Вычислить».

Способ Крамера

Метод Крамера используют для решения квадратной системы уравнений, представленной в линейном виде, где определитель основной матрицы не равен нулю. Считается, что система обладает единственным решением. Например, задана система линейных уравнений:

Её необходимо заменить равноценным матричным уравнением.

Второй столбец вычисляют, а первый уже задан. Есть предположение, что определитель матрицы отличен от нуля. Из этого можно сделать выводы, что существует обратная матрица. Перемножив эквивалентное матричное уравнение на обратного формата матрицу, получим выражение:

В итоге получают выражения:

Из представленных уравнений выделяют формулы Крамера:

Метод Крамера не представляет сложности. Он может быть описан следующим алгоритмом:

Проверить решение матрицы методом Крамера онлайн позволяет калькулятор автоматического расчёта. Для получения быстрого ответа в представленные поля подставляют переменные числа и их количество. Дополнительно может потребоваться указание вычислительного метода разложения по строке или столбу. Другой вариант заключается в приведении к треугольному виду.

Указывается также представление чисел в виде целого числа, обыкновенной или десятичной дроби. После введения всех предусмотренных параметров и нажатия кнопки «Вычислить» получают готовое решение.

Источник

Транспонирование матрицы, умножение, возведение в степень

Как мы выяснили в предыдущей статье, с матрицами можно выполнять различные простые операции, такие как сложение, вычитание, умножение и т.д. Они называются простыми, поскольку имеют аналогии с операциями над обычными числами.

Но существуют и такие операции как транспонирование матрицы, произведение двух матриц и возведение матрицы в степень. Они уже имеют свой уникальный алгоритм действий, который мы сейчас разберем.

Итак, приступим к практике.

1. Транспонирование матрицы

Простым языком – это переворачивание матрицы, то есть первая строка превращается в первый столбец, вторая строка превращается во второй столбец, третья строка превращается в третий столбец и так далее.

Пусть дана матрица размером 4×3:

2. Произведение матриц

Рассмотрим такое произведение матриц:

ВАЖНО! Матрицы должны быть согласованными, то есть число столбцов в первой матрице А_{3х 3} должно совпадать с числом строк во второй матрице B _{3 х2}. Если этого не происходит, значит провести умножение матриц невозможно.

2.1. Первым делом нам необходимо выяснить размер матрицы C. Для этого мы берем количество строк А_{3х 3} и количество столбцов B _{3 х2} и получаем, что матрица будет состоять из 3 строк на 2 столбцов.

2.2. Далее необходимо вычислить каждый элемент матрицы C. Для этого мы обращаем внимание на индекс каждого элемента. Первый индекс числа c _{1 1} отвечает за номер строки в первой матрице, а второй индекс (c_{1 1} ) отвечает за номер столбца во второй матрице.

Исходя из этой информации, необходимо вычислить сумму произведений всех элементов в соответствующих сроках и столбцах.

2.3. Аналогично получаем остальные элементы:

Необходимо помнить ПРАВИЛО, что A*B≠B*A. Это равенство будет выполняться только в том случае, если матрицы A и B являются перестановочными.

3. Возведение матрицы в степень

Для этого необходимо умножать матрицу на саму себя то число раз, которое указано в степени.

Теперь произведем вычисления:

Умножение происходит по алгоритму, описанному выше.

Можно заметить, что количество вычислений становится все больше и больше, поэтому советуем всегда перепроверять полученный результат.

Источник

Некоторые свойства операций над матрицами.
Матричные выражения

На базовых уроках Действия с матрицами, Как найти обратную матрицу? мы познакомились с понятием матрицы и основными операциями над матрицами. При этом основные акценты были подробно расставлены на технических приёмах вычисления, чтобы совершенно неподготовленный человек смог быстро научиться решать матрицы. Поэтому чайникам следует начать с первых двух статей и лягушатника с определителем матрицы. Из инструментальных средств рекомендую запастись матричным калькулятором, который позволит контролировать весь процесс решения и не допустить ошибок. Найти его можно, например, на складе математических формул и таблиц.

А сейчас последует продолжение темы, в котором мы рассмотрим не только новый материал, но и отработаем действия с матрицами.

Некоторые свойства операций над матрицами

Существует достаточно много свойств, которые касаются действий с матрицами, в той же Википедии можно полюбоваться стройными шеренгами соответствующих правил. Однако на практике многие свойства в известном смысле «мертвЫ», поскольку в ходе решения реальных задач используются лишь некоторые из них. Моя цель – рассмотреть прикладное применение свойств на конкретных примерах, и если вам необходима строгая теория, пожалуйста, воспользуйтесь другим источником информации.

Но сначала вернёмся к действиям с матрицами (к слову, в той статье мы уже неявно затронули ряд свойств). Начну с небольшого вопроса, который вызвал трудности у некоторых посетителей сайта:

Можно ли к матрице прибавить число?

Например: 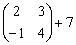. Ну, или наоборот:

Нет. К матрице можно прибавить только другую матрицу, причём точно такого же размера.

Матрицу можно умножить на число. Но сложить их нельзя. Таковы правила игры.

Следует отметить, что допустимо сложение определителя матрицы с числом:

Результат вычисления определителя – число, а два числа суммируются без всяких проблем.

Вышесказанное, естественно, справедливо и для разности, ведь вычитание – это частный случай сложения.

Как на счёт того, чтобы плотно зависнуть у меня сегодня вечером? =) Практика показывает, что наибольшие трудности у студентов вызывает умножение матриц. Так наполним же кружки соответствующей информацией.

Повторим само правило. В статье Действия с матрицами я рассказал о том, какие матрицы можно умножать и привёл ряд наиболее распространённых примеров. Давайте рассмотрим операцию чуть подробнее и выделим два существенных пункта:

1) Смотрим на левую часть. Из первого урока нам известно, что матричное умножение возможно в том и только в том случае, если количество столбцов первой матрицы равно количеству строк второй матрицы.

2) Смотрим на правую часть и обращаем внимание на размерность результата – СКОЛЬКО строк и столбцов должно быть у итоговой матрицы.

Умножить матрицы

Решение: произведение существует, причём итоговая матрица состоит из 1 строки и 2 столбцов:

Ответ:

Умножить матрицы

Это пример для самостоятельного решения.

Предложенные примеры не случайны. Они вроде бы просты, но у начинающих здесь нередко возникает путаница с размерами матрицы-результата. Поэтому читателям с небольшим опытом целесообразно переписать вышеприведённую формулу и особенно серьёзно отнестись к практическим примерам.

А по каким принципам составляются начинка (суммы произведений чисел), думаю, все уже поняли. Дополнительно возьмём на вооружение образную ассоциацию, которая поможет хорошо запомнить действие. Читаем следующий параграф:

Как возвести матрицу в квадрат?

Операция определена только для квадратных матриц – «два на два», «три на три» и т.д.

Возвести квадратную матрицу в квадрат – это значит, умножить её саму на себя:

Возвести в квадрат матрицу

Решение: пример рутинный, и чтобы извлечь максимальную пользу, давайте закрепим очень распространённый случай умножения двух матриц «три на три»:

Строки первой матрицы – это столы в ресторане, а цветные столбцы второй матрицы – официанты. Сначала столы обслуживает красный официант, затем зелёный официант, и под конец застолья – синий официант. Тааак, хватит прикалываться, он не голубой =)

Это действительно удобный мысленный приём, который можно использовать на практике – последовательно (слева направо) перебираем столбцы второй матрицы и «пристраиваем» их к каждой строке первой матрицы.

Ответ:

Возведение матрицы в куб и более высокие степени разберём позже.

Немного о некоммутативности матричного умножения и единичной матрице

Материал, по меньшей мере, частично вам знаком. Для тех, кто не знает термина:
Коммутативность = Перестановочность.

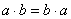
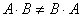
Обычные числа переставлять можно: , а матрицы в общем случае не перестановочны: . Собственно, подробная иллюстрация с конкретными примерами уже была дана в статье Действия с матрицами.

Рассмотрим некоторые исключения из правила, которые потребуются для выполнения практических задач.

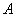
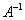
Если у квадратной матрицы существует обратная матрица , то их умножение коммутативно:

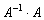
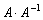
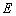
Чтобы проверить, правильно ли найдена обратная матрица, нужно вычислить произведение либо произведение и убедиться в том, что получится единичная матрица . Конкретные примеры можно посмотреть в статье Как найти обратную матрицу?

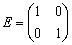
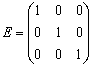
Единичной матрицей называется квадратная матрица, у которой на главной диагонали расположены единицы, а остальные элементы равны нулю. Например: , и т.д.

При этом справедливо следующее свойство: если произвольную матрицу 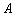умножить слева или справа на единичную матрицу подходящих размеров, то в результате получится исходная матрица:

Как видите, здесь также имеет место коммутативность матричного умножения.

Возьмём какую-нибудь матрицу, ну, скажем, матрицу из предыдущей задачи: .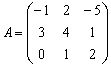

Желающие могут провести проверку и убедиться, что:

Единичная матрица для матриц – это аналог числовой единицы для чисел, что особенно хорошо видно из только что рассмотренных примеров.

Коммутативность числового множителя относительно умножения матриц

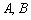
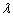
Для матриц и действительного числа справедливо следующее свойство:

То есть числовой множитель можно (и нужно) вынести вперёд, чтобы он «не мешал» умножить матрицы.

Примечание: вообще говоря, формулировка свойства неполная – «лямбду» можно разместить в любом месте между матрицами, хоть в конце. Правило остаётся справедливым, если перемножаются три либо бОльшее количество матриц.

Вычислить произведение

Решение:

(1) Согласно свойству 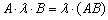перемещаем числовой множитель вперёд. Сами матрицы переставлять нельзя!

(2) – (3) Выполняем матричное умножение.

(4) Здесь можно поделить каждое число 10, но тогда среди элементов матрицы появятся десятичные дроби, что не есть хорошо. Однако замечаем, что все числа матрицы делятся на 5, поэтому умножаем каждый элемент на .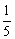

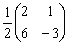
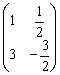
Окончательный ответ лучше оставить в виде , хотя, в принципе, годится и внесение дроби: . На технических тонкостях умножения матрицы на число я подробно останавливался на уроке Действия с матрицами.

Ответ:

Маленькая шарада для самостоятельного решения:

Вычислить 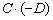, если

Решение и ответ в конце урока.

Какой технический приём важен в ходе решения подобных примеров? С числом разбираемся в последнюю очередь.

Прицепим к локомотиву ещё один вагон:

Как умножить три матрицы?

Прежде всего, ЧТО должно получиться в результате умножения трёх матриц 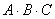? Кошка не родит мышку. Если матричное умножение осуществимо, то в итоге тоже получится матрица. М-да, хорошо мой преподаватель по алгебре не видит, как я объясняю замкнутость алгебраической структуры относительно её элементов =)

Произведение трёх матриц 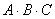можно вычислить двумя способами:

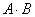
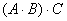
1) найти , а затем домножить на матрицу «цэ»: ;

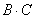
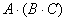
2) либо сначала найти , потом выполнить умножение .

Результаты обязательно совпадут, и в теории данное свойство называют ассоциативностью матричного умножения:

Перемножить матрицы двумя способами

Алгоритм решения двухшаговый: находим произведение двух матриц, затем снова находим произведение двух матриц.

1) Используем формулу

Действие первое:

Действие второе:

2) Используем формулу

Действие первое:

Действие второе:

Ответ:

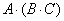
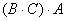
Более привычен и стандартен, конечно же, первый способ решения, там «как бы всё по порядку». Кстати, по поводу порядка. В рассматриваемом задании часто возникает иллюзия, что речь идёт о каких-то перестановках матриц. Их здесь нет. Снова напоминаю, что в общем случае ПЕРЕСТАВЛЯТЬ МАТРИЦЫ НЕЛЬЗЯ. Так, во втором пункте на втором шаге выполняем умножение , но ни в коем случае не . С обычными числами такой бы номер прошёл, а с матрицами – нет.

Свойство ассоциативности умножения справедливо не только для квадратных, но и для произвольных матриц – лишь бы они умножались:

Найти произведение трёх матриц

Это пример для самостоятельного решения. В образце решения вычисления проведены двумя способами, проанализируйте, какой путь выгоднее и короче.

Свойство ассоциативности матричного умножения имеет место быть и для бОльшего количества множителей.

Теперь самое время вернуться к степеням матриц. Квадрат матрицы рассмотрен в самом начале и на повестке дня вопрос:

Как возвести матрицу в куб и более высокие степени?

Данные операции также определены только для квадратных матриц. Чтобы возвести квадратную матрицу 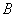в куб, нужно вычислить произведение:

Фактически это частный случай умножения трёх матриц, по свойству ассоциативности матричного умножения: 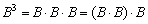. А матрица, умноженная сама на себя – это квадрат матрицы:

Таким образом, получаем рабочую формулу:

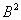
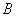
То есть задание выполняется в два шага: сначала матрицу необходимо возвести в квадрат, а затем полученную матрицу умножить на матрицу .

Возвести матрицу 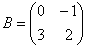в куб.

Это небольшая задачка для самостоятельного решения.

Возведение матрицы в четвёртую степень проводится закономерным образом:

Используя ассоциативность матричного умножения, выведем две рабочие формулы. Во-первых: 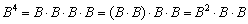– это произведение трёх матриц.

1) . Иными словами, сначала находим , затем домножаем его на «бэ» – получаем куб, и, наконец, выполняем умножение ещё раз – будет четвёртая степень.

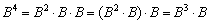
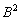
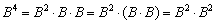
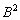
2) Но существует решение на шаг короче: . То есть, на первом шаге находим квадрат и, минуя куб, выполняем умножение

Дополнительное задание к Примеру 8:

Возвести матрицу 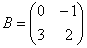в четвёртую степень.

Как только что отмечалось, сделать это можно двумя способами:

1) Коль скоро известен куб, то выполняем умножение .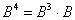

2) Однако, если по условию задачи требуется возвести матрицу только в четвёртую степень, то путь выгодно сократить – найти квадрат матрицы и воспользоваться формулой .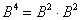

Оба варианта решения и ответ – в конце урока.

Аналогично матрица возводится в пятую и более высокие степени. Из практического опыта могу сказать, что иногда попадаются примеры на возведение в 4-ю степень, а вот уже пятой степени что-то не припомню. Но на всякий случай приведу оптимальный алгоритм:

1) находим ;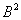
2) находим ;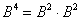
3) возводим матрицу в пятую степень: .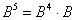

Вот, пожалуй, и все основные свойства матричных операций, которые могут пригодиться в практических задачах.

Во втором разделе урока ожидается не менее пёстрая тусовка.

Матричные выражения

Повторим обычные школьные выражения с числами. Числовое выражение состоит из чисел, знаков математических действий и скобок, например: 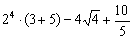. При расчётах справедлив знакомый алгебраический приоритет: сначала учитываются скобки, затем выполняется возведение в степень / извлечение корней, потом умножение / деление и в последнюю очередь – сложение /вычитание.

Если числовое выражение имеет смысл, то результат его вычисления является числом, например:

Матричные выражения устроены практически так же! С тем отличием, что главными действующими лицами выступают матрицы. Плюс некоторые специфические матричные операции, такие, как транспонирование и нахождение обратной матрицы.

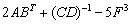
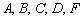
Рассмотрим матричное выражение , где – некоторые матрицы. В данном матричном выражении три слагаемых и операции сложения/вычитания выполняются в последнюю очередь.

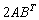
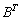
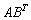
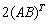
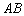
В первом слагаемом сначала нужно транспонировать матрицу «бэ»: , потом выполнить умножение и внести «двойку» в полученную матрицу. Обратите внимание, что операция транспонирования имеет более высокий приоритет, чем умножение. Скобки, как и в числовых выражениях, меняют порядок действий: – тут сначала выполняется умножение , потом полученная матрица транспонируется и умножается на 2.

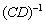
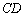
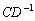
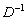
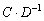
Во втором слагаемом в первую очередь выполняется матричное умножение , и обратная матрица находится уже от произведения. Если скобки убрать: , то сначала необходимо найти обратную матрицу , а затем перемножить матрицы: . Нахождение обратной матрицы также имеет приоритет перед умножением.

С третьим слагаемым 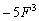всё очевидно: возводим матрицу в куб и вносим «пятёрку» в полученную матрицу.

Если матричное выражение имеет смысл, то результат его вычисления является матрицей.

Все задания будут из реальных контрольных работ, и мы начнём с самого простого:

Даны матрицы 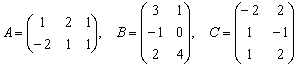. Найти:

Решение: порядок действий очевиден, сначала выполняется умножение, затем сложение.

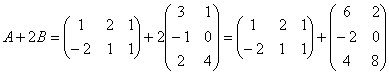
Сложение выполнить невозможно, поскольку матрицы разных размеров.

Не удивляйтесь, заведомо невозможные действия часто предлагаются в заданиях данного типа.

Пробуем вычислить второе выражение:

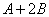
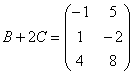
Ответ: действие выполнить невозможно, .

Даны матрицы .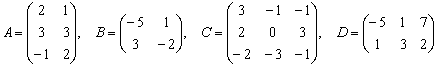

Найти значения выражений:

Решение: Разбираемся с произведением 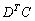. Сначала транспонируем матрицы «дэ»:

И умножаем матрицы:

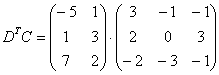
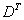
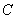
Матричное умножение выполнить невозможно, так как число столбцов матрицы не равно числу строк матрицы .

А вот с произведением 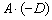проблем не возникает:

Еще раз заметьте, как на первом же шаге множитель (–1) выносится вперёд, и ноги до него доходят в самую последнюю очередь.

С более сложными выражениями вроде 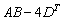чайникам рекомендую разбираться поэтапно, чтобы не запутаться:

Сначала находим произведение:

Затем считаем второе слагаемое:

И, наконец, всё выражение:

Более подготовленные студенты могут оформить решение одной строкой:

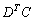
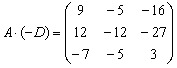
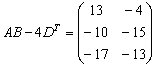
Ответ: действие выполнить невозможно, , .

Пара заключительных примеров для самостоятельного решения:

Для матриц Примера №10 выполнить действия:

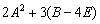
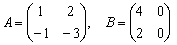
Вычислить значение матричного многочлена , если .

В последнем примере решение удобно оформить по пунктам.

Матричные выражения – это просто! И вряд ли на практике вам встретится что-то сложнее, чем разобранные примеры.

Теперь во всеоружии можно приступить к изучению матричных уравнений.

Пример 2: Решение: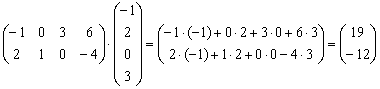

Ответ:

Пример 5: Решение: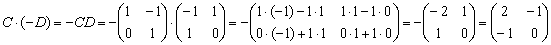

Ответ:

Пример 7: Решение:
1) Используем формулу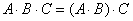

2) Используем формулу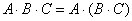

Ответ:

Пример 8: Решение: Сначала возведём матрицу в квадрат: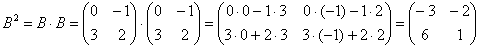

Возведём матрицу в куб: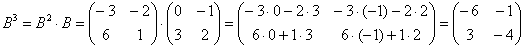

Возведём матрицу в четвёртую степень двумя способами: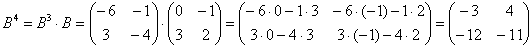


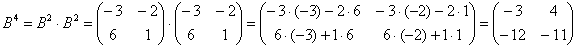
Ответ:

Пример 11: Решение:

Возведение в квадрат 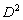невозможно, поскольку операция определена только для квадратных матриц.

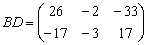
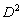
Ответ: , действие выполнить невозможно,

Пример 12: Решение:
1)
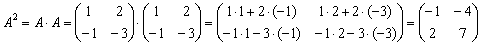
2)
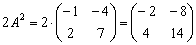
3)
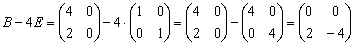
4)
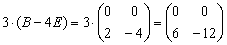
5)
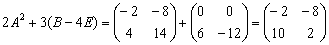
Ответ: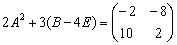
Примечание: выражение можно было вычислить и по-другому – предварительно раскрыть скобки:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник