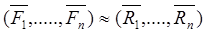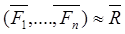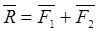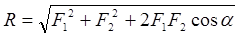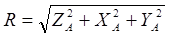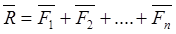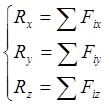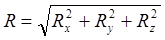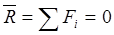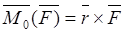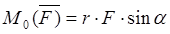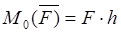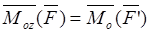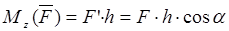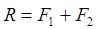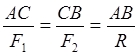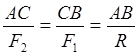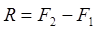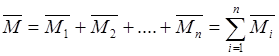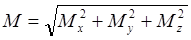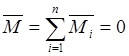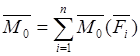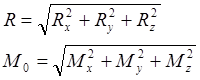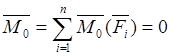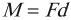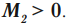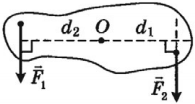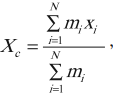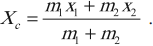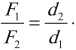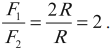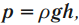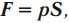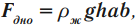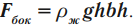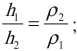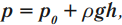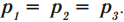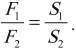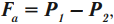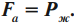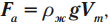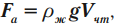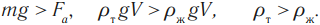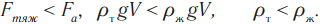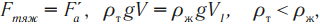Что означает статика какие задачи она решает

Что означает статика какие задачи она решает

1.Предмет и задачи статики.

Статика-это раздел теоретической механики, который изучает преобразование системы сил и условия равновесия под действием сил.

Статика решает две основные задачи:

Сложение или разложение сил и приведение системы сил к простейшему виду.

Отыскание условий равновесия системы сил.

К основным понятиям статики относят:

1. Материальная точка — это физическое тело определенной массы, размерами которого можно пренебречь в данных условиях.

2. Система материальных точек — это такая совокупность точек, в которой положение и движение каждой определенной точки зависит от положения и движения других точек системы.

3. Абсолютно твердое тело — это тело, в котором расстояния между любыми двумя его точками остается неизменным.

В статике основным объектом исследования являются силы. Сила — это мера механического взаимодействия между телами, которое определяет интенсивность и направление этого воздействия.

Сила- величина векторная и характеризуется модулем, направлением и точкой приложения или линией действия. В системе СИ измеряется в ньютонах(Н). Когда на тело действует несколько сил, то их совокупность называется системой сил.

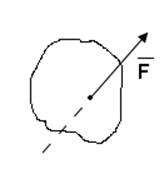
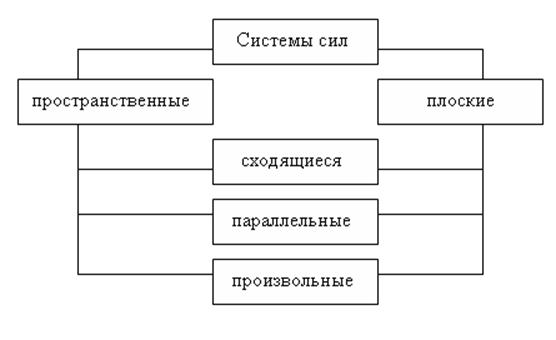
Эти системы, в зависимости от их ориентации, разделяются на следующие:

Параллельные силы — линии действия параллельны.

Сходящиеся — линии действия которых пересекаются в одной точке.

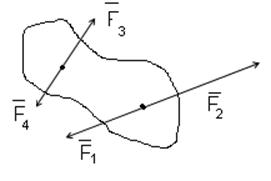
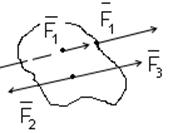
Произвольная система сил — силы могут занимать любое положение в пространстве.

Силы разделяются также на активные и реакции связей, сосредоточенные и распределенные, внутренние и внешние, плоские и пространственные.

Сосредоточенной силой называется сила, прилагаемая к объекту в одной точке. Распределенными силами называют силы, которые действуют на все точки поверхности или объема тела. При решении задач распределенные силы заменяют сосредоточенными согласно правилу:

[H].

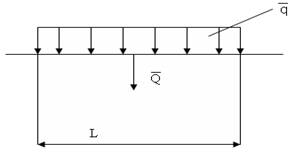
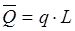
Две системы силы называют эквивалентными, если одну систему сил можно заменить другой, не изменяя покоя или движения тела:

Когда система сил эквивалентна одной силе, то эта сила имеет название равнодействующей.

Уравновешенной называется такая система сил, добавление которой к свободному твердому телу или её отбрасывание не изменяют состояния покоя или движения этого тела. Уравновешенная система сил эквивалентна нулю.

В основе статики лежат её аксиомы. Аксиомой называется положение, не требующее доказательств, исходной для других положений и теорем.

Аксиома 1. Две силы, которые действуют на твердое тело, уравновешиваются только тогда, когда они равны по модулю, противоположны по направлению и действуют вдоль одной прямой.

Аксиома 2. Действие данной системы сил на твердое тело не изменяется, если к ней прибавить или от неё отбросить систему сил эквивалентную нулю.

Следствие: не нарушая состояния тела, точку приложения силы можно переносить вдоль линии её действия.

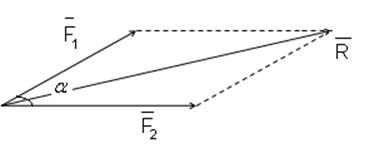
Аксиома 3. Равнодействующая двух сил, которые пересекаются, равна диагонали параллелограмма, построенного на этих силах, как на сторонах. Тогда:

Аксиома 4. Силы, с которыми действуют друг на друга тела, всегда равны по модулю и направлены в противоположные вдоль одной прямой стороны.

Силы взаимодействия двух тел не составляют систему уравновешивающих сил, т. к они приложены к разным телам.

Аксиома 5. Равновесие деформируемого тела не нарушается, если жестко связать его точки и считать тело абсолютно твердым (используется для тел, которые нельзя считать твердыми).

Аксиома 6. Механическое состояние твердого тела не нарушается, если отбросить связи и заменить их действие реакциями.

Аксиома 7. Равновесие твердого тела не нарушается, если наложит на него новые связи.

3. Основные типы связей.

Связь — это ограничение, наложенное на движение точек материальной системы. Отбрасывая связь, её действие заменяют силой, которая называется реакцией связи, т. е противодействием связи на действие данного тела. Роль связей на практике выполняют разные тела и конструкции, основными из которых есть:

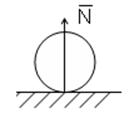
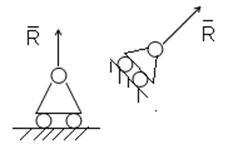
1.Идеально гладкая поверхность. 2.Ребро поверхности.

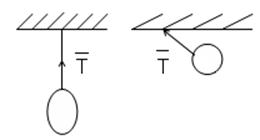
3.Подвижный шарнир(каток) 4.Невесомая нить(трос, шнур, цепь, ремень)

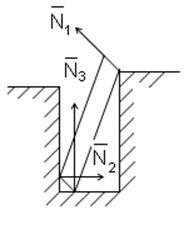
5.Цилиндрический шарнир 6.Идеальный стержень

7.Сферический шарнир или 8.Жесткая заделка

9.Подшипник 10.Жесткая заделка по двум степеням свободы

4. Силы и системы сил.

Классификацию сил мы рассмотрели выше. Для системы сил можно предложить следующую классификацию:

Пространственной системой называют систему сил, линии действия которых в общем случае не пересекаются. Плоская система — линии действия расположены в одной плоскости.

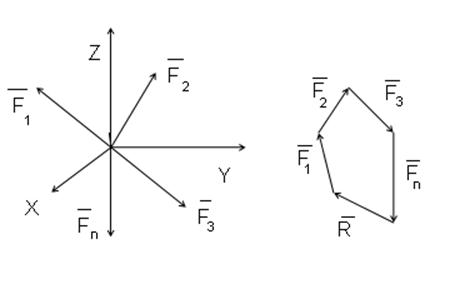
5.Система сходящихся сил (ССС)

Такой системой называется совокупность сил, линии действия которых пересекаются в одной точке.

Система сходящихся сил является наиболее простой системой сил в пространстве и на плоскости с наиболее простыми условиями равновесия.

Если в результате построения силового многоугольника окажется, что конец вектора последней n-ой силы совпадает с началом вектора 1-ой силы, т. е силовой многоугольник будет замкнутым, то равнодействующая такой системы будет равна нулю. В этом случае действие сходящейся системы сил эквивалентна нулю и мы можем записать:

Таким образом, геометрическим (или векторным) условием равновесия ССС является условие равенства нулю её равнодействующей: для равновесия ССС необходимо и достаточно, чтобы силовой многоугольник был замкнутым.

Аналитическое условие равновесия: для равновесия сходящейся системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на координатные оси равнялась нулю.

6. Понятие проекции силы.

Проекцией силы на ось называется алгебраическая величина, равная произведению модуля силы на cos угла между вектором силы и положительным направлением оси. Проекция имеет положительный знак в том случае, если этот угол острый, если тупой- отрицательный, если , то она равна нулю.

Момент силы относительно точки

Моментом силы Относительно точки О (центра) называется вектор, который равняется векторному произведению радиус-вектора , проведенного из центра О в точку А приложения силы, на вектор :

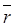
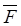
Модуль этого векторного произведения:

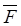
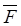
Опустим перпендикуляр из точки О на линию действия силы. Длина этого перпендикуляра OD=h называется плечом силы относительно точки О. Тогда:

Если переместить силу вдоль линии её действия, то момент силы относительно точки не изменится;

Когда линия действия силы проходит через точку, то момент силы относительно этой точки всегда равен нулю.

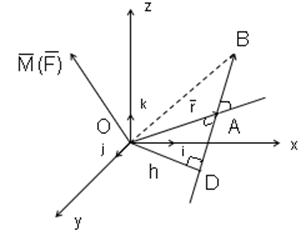
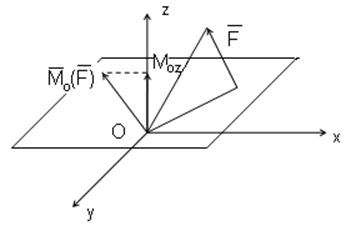
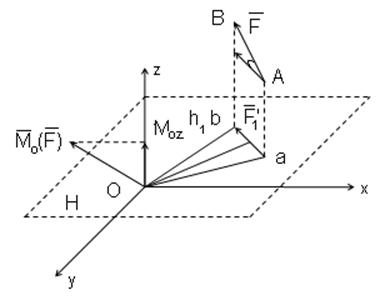
8. Момент силы относительно оси.

Моментом силы относительно оси называется проекция на эту ось момента силы относительно любой точки, лежащей на этой оси.

Если момент силы относительно некоторого центра О вызывает вращательное движение тела вокруг этого центра, то момент силы относительно оси вызывает вращение тела вокруг данной оси.

При решении задач моменты сил относительно осей удобно вычислять наглядным способом по правилу:

Проводим плоскость и произвольно и перпендикулярно к оси OZ и находим точку О, пересечения этой плоскости осью.

Проектируем силу 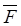на отмеченную плоскость.

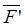
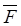
Вычисляем момент проекции Силы на эту плоскость относительно точки О:

При этом моменты силы относительно оси считается положительным, если наблюдатель видит со стороны положительного направления оси OZ, что сила 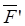пытается вращать тело вокруг оси OZ против стрелки часов.

Численно момент будет равен:

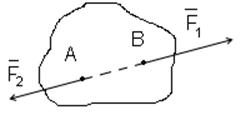
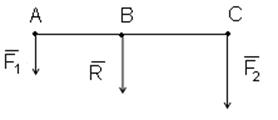
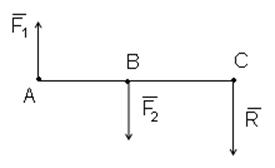
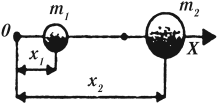
1.Сложение параллельных сил, которые направлены в одну сторону

Равнодействующая этих сил (её модуль) будет равна:

Линия действия равнодействующей в этом случае пересекает отрезок АВ в точке С, которая делит этот отрезок на части, обратно пропорциональные модулям сил:

Т. е равнодействующая двух параллельных сил, направленных в одну сторону, по одну сторону, по модулю равна сумме модулей этих сил, направлена в ту же сторону, что и силы, и делит расстояние между точками приложения сил на отрезки, обратно пропорциональные силам.

2.Сложение параллельных сил, направленных в противоположные стороны.

Равнодействующая двух параллельных сил, направленных в разные стороны, по модулю равна разнице модулей этих сил, направлена в сторону большей силы и делит расстояние между точками приложения обратно пропорционально модулям сил.

В том случае, если силы 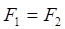, то модуль равнодействующей равен нулю.

Однако действие пары сил на тело не равно нулю и вызывает вращательное движение.

Мерой вращательного движения пары сил служит момент пары, величина которого определяется по формуле:

[Hм]

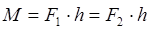
В этом случае плечо h — это кротчайшее расстояние между линиями действия параллельных сил.

Направление вращения, созданного парой сил, определяет знак момента пары: если пара сил вращает тело против часовой стрелки — момент положительный, если наоборот — отрицательный.

Момент пары сил имеет величину, направление и плоскость действия, т. е векторной величиной.

Вектор момента пары сил перпендикулярен к плоскости, в которой лежит, и направлен в ту сторону, откуда вращается тело, под действием пары в сторону против хода часовой стрелки.

Пару сил, не изменяя её действия на тело, можно перенести куда угодно в плоскости, в которой лежит пара.

Пару сил, не изменяя её действия на тело, можно перенести в параллельную плоскость.

В паре сил, не изменяя её момента, можно изменять соответственно модули сил и длину плеча.

Две пары сил с равными моментами эквивалентны.

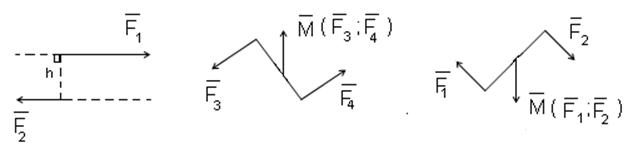
Несколько пар сил, которые лежат в одной плоскости, можно заменить одной эквивалентной парой с моментом, который равняется векторной сумме моментов этих пар.

На основании пятого вывода можно записать:

На основании теоремы о проекциях суммы векторов можно записать:

; ; ;

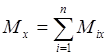
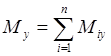
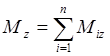
Модуль момента пары:

Таким образом для равновесия пар необходимо и достаточно, чтобы вектор-момент равнодействующей пары был равен нулю:

Т. е ; ;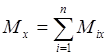

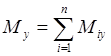
Произвольная система сил.

Произвольной системой сил называется совокупность прилагаемых к твердому телу сил, лини действия которых произвольно ориентированы в пространстве.

Произвольную систему сил можно свести к одной равнодействующей силе, которая равна главному вектору, прилагаемому в центре сведения и к одной паре сил, которая равна главному моменту относительно того же центра:

;

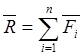
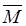
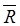
Модули векторов И Определяют по формулам:

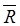
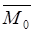
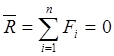
В результате для произвольной системы сил твердое тело, находящееся под действием этой системы, будет находиться в равновесии, если главный вектор И главный момент системы будут равны нулю:

;

Проектируя эти уравнения декартовы оси координат, запишем аналитические условия равновесия произвольной пространственной системы сил, читаются следующим образом:

Для равновесия произвольной системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на три взаимно взаимно перпендикулярные оси и сумма моментов всех сил относительно этих осей равнялась нулю:

Источник

Статика

Статика – это раздел механики, изучающий условия равновесия тел.

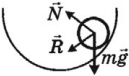
Виды равновесия тел

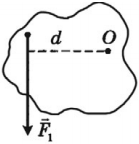
Момент силы

Момент силы – это физическая величина, равная произведению модуля силы на ее плечо.

Обозначение – ​ \( M \) ​, единицы измерения – Н·м.

где ​ \( d \) ​ – плечо силы ​ \( F \) ​.

Плечо силы – это кратчайшее расстояние (перпендикуляр) от оси вращения до прямой, вдоль которой действует сила.
Обозначение – ​ \( d \) ​ или ​ \( l \) ​, единицы измерения – м.

Знак момента силы

Если сила, приложенная к телу, вращает его по часовой стрелке, то момент силы положителен (​ \( M \) ​ > 0):

Если сила, приложенная к телу, вращает его против часовой стрелки, то момент силы отрицателен ( \( M \) Условия равновесия тел

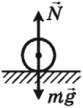
Тело находится в равновесии, если

Центр тяжести – это точка внутри тела или вне его, относительно которой сумма моментов сил тяжести, действующих на отдельные его части, равна нулю.
Центр масс – геометрическая точка, положение которой характеризует распределение масс в теле:

Важно!
Для твердого тела центр тяжести совпадает с центром масс.

Простые механизмы

Простые механизмы – это приспособления, служащие для преобразования силы.

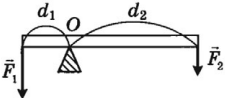
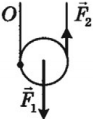
Рычаг – это простейшее механическое устройство, представляющее собой твердое тело (перекладину), вращающееся вокруг точки опоры.

Рычаг дает выигрыш в силе:

Блок — простое механическое устройство, представляющее собой колесо с желобом по окружности, вращающееся вокруг своей оси. Желоб предназначен для каната, цепи, ремня и т. п.
Блок бывает подвижный и неподвижный.

Неподвижный блок – это блок, ось которого закреплена.

Неподвижный блок не дает выигрыша в силе, он используется для изменения направления действия силы.

Подвижный блок – это блок, имеющий свободную ось.

Подвижный блок дает выигрыш в силе в 2 раза:

«Золотое правило» механики

При использовании простых механизмов во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, т. е. простые механизмы выигрыша в работе не дают.

Давление жидкости

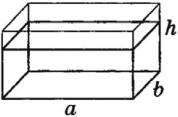
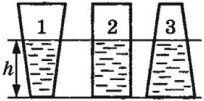
Давление жидкости – это величина, равная произведению плотности жидкости на модуль ускорения свободного падения и на высоту столба жидкости.

где ​ \( \rho \) ​ – плотность жидкости,
​ \( h \) ​ – высота столба жидкости.

Сила давления жидкости – это сила, равная произведению давления жидкости на площадь поверхности:

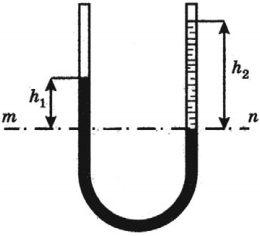
Сообщающиеся сосуды

Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости.

Закон сообщающихся сосудов:
в неподвижных и открытых сообщающихся сосудах любой формы давление жидкости на любом горизонтальном уровне одинаково.

Следствия из закона сообщающихся сосудов:

Важно!
Давление, которое создает жидкость, находящаяся в равновесии при действии на нее силы тяжести, называют гидростатическим. Гидростатическое давление определяется формулой ​ \( p=\rho gh \) ​.
Давление внутри жидкости на любой глубине складывается из атмосферного давления, или внешнего давления на жидкость, и гидростатического давления:

где ​ \( p_0 \) ​ – атмосферное давление.

Закон Паскаля

Закон Паскаля
Давление, производимое на жидкость или газ, передается по всем направлениям одинаково.

Следствие из закона Паскаля — гидростатический парадокс: давление, производимое на дно сосуда, зависит только от высоты столба жидкости:

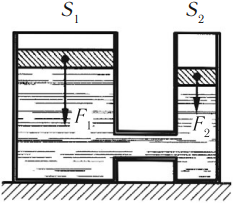
Сила давления жидкости на дно разная, т.к. она зависит от площади дна:

Гидравлический пресс – два сообщающихся сосуда, заполненные жидкостью и закрытые поршнями различной площади.
Гидравлический пресс дает выигрыш в силе, но проигрыш в длине пути поршня:

Силы, действующие на поршни гидравлического пресса, пропорциональны площадям этих поршней:

Атмосферное давление – это давление, которое оказывает атмосфера на все находящиеся в ней предметы.
Атмосферное давление уменьшается с увеличением высоты подъема над Землей.

Нормальное атмосферное давление: ​ \( p_0 \) ​ = 10 5 Па.

Приборы для измерения давления:

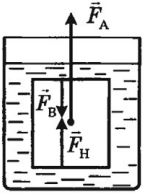
Закон Архимеда

Архимедова сила – это выталкивающая сила, действующая на тело, погруженное в жидкость или газ.

Причина возникновения выталкивающей силы – разница давлений жидкости или газа на верхнюю и нижнюю грани.
Архимедова сила всегда направлена перпендикулярно поверхности жидкости.
Архимедова сила равна разности веса тела в воздухе и веса тела в жидкости или газе:

где ​ \( P_1 \) ​ – вес тела в воздухе,
​ \( P_2 \) ​ – вес тела в жидкости или газе.

Закон Архимеда
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу жидкости или газа, вытесненных телом:

Если тело полностью погружено в жидкость, то

где ​ \( V_m \) ​ – объем тела, погруженного в жидкость.

Если тело не полностью погружено в жидкость, то

где ​ \( V_ <чm>\) ​ – объем части тела, погруженной в жидкость.

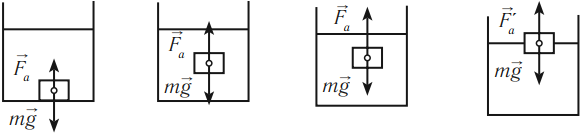
Условия плавания тел

На любое тело, погруженное в жидкость или газ, действуют две силы, направленные в противоположные стороны, – это сила тяжести и архимедова сила. Направление движения тела зависит от того, какая из этих сил больше по модулю.

Условия плавания тел

где ​ \( V_1 \) ​ – объем части тела, погруженной в жидкость.

Важно!
Выталкивающая сила действует на тела в жидкостях и газах, потому что сжаты силой притяжения к Земле. В состоянии невесомости эта сила не действует.

Источник