Что означает сравни выражения в математике 4 класс
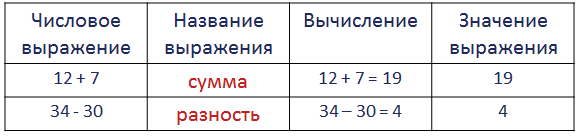
Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Значение выражения — это результат выполненных действий.
Чтение числовых выражений
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Для этого найдем значения каждого из них:
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
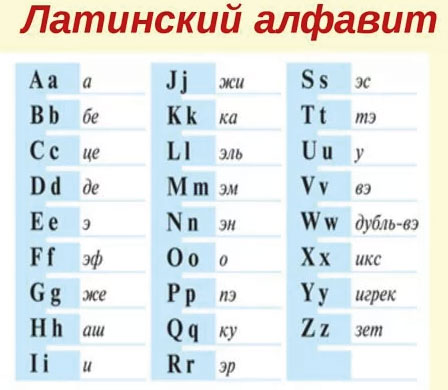
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Поделись с друзьями в социальных сетях:
Числовые и буквенные выражения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
14 больше 4
14 > 4
6 + 8 > 2 * 2
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Пример 1. Найдите значение выражения: 5 + x.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Урок математики в 4-м классе «Сравнение чисел»
— Сегодня я вам предлагаю провести очередной тур игры «Что? Где? Когда?» между знатоками 4а и 4б классов. В этом туре вы отвечаете на вопросы знатоков 4а класса. Для проведения игры, которая состоит из четырех раундов, вам необходимо разделиться по группам-командам.
Назовите вариант ответа, в котором цифра 5 стоит в разряде десятков:
Определите правильную запись числа шесть тысяч девять:
Назовите правильную запись числа 975 в виде суммы разрядных слагаемых:
Назовите те выражения, значения которых содержат тридцать десятков (предлагается работа в черновиках):
— С какими числами вы работали? (ответы учащихся);
— Сегодня мы продолжим работу с натуральными числами.
РАБОТА НАД НОВОЙ ТЕМОЙ
«Найти закономерность, заполнить «окошки» в таблице и ответить на вопросы»
СРАВНЕНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ
(запись на мультимедиа)
— Цель нашего урока: Вывести правило сравнения чисел и научиться его применять.
(ЗАПИСЬ в тетради числа, темы урока)
Составление 1 алгоритма сравнения чисел
— Каким способом можно сравнивать числа?
— На какие знания вы опирались при сравнении чисел? (ответы учащихся)
Составление 1 алгоритма
— Чтобы сравнить два числа мы должны сделать первый шаг:
(запись на мультимедиа)
— Значить оно по сравнению с числом 90 будет больше или меньше? (ответы учащихся)
— Значить оно будет больше или меньше? (ответы учащихся)
— Значит, оно будет больше или меньше? (ответы учащихся)
— Значит, оно будет больше или меньше? (ответы учащихся)
Вывод: вы проговорили правило сравнения натуральных чисел с помощью алгоритма. В дальнейшем вы еще не раз будете составлять алгоритмы.
— Для закрепления правила вам предлагается сравнить числа
Закрепление применения 1 алгоритма.
(запись на мультимедиа)
Взаимопроверка в парах, сравнение с правильными ответами.
Закрыли глазки. Вдохнули глубоко. Задержали дыхание, выдохнули. (повторяется 3 раза). Подняли руки вверх, потянулись. Опустили руки на парты.
Зафиксировали взгляд на тренажере и повторили упражнения для глаз. (3 раза)
4) Составление 2 алгоритма сравнения чисел
а) О каких величинах говорится в задаче?
(о времени работы рабочего и ученика, о количестве вытачиваемых деталей рабочим и учеником, об изготовлении за час)
б) Уточним, какие числовые значения соответствуют этим величинам.
Поиск решения задачи.
— Можно ли сразу узнать, на сколько деталей за 1 час больше вытачивает рабочий, чем ученик? (Нет, так как мы не знаем, сколько за 1 час вытачивает рабочий и сколько за 1 час вытачивает ученик)
— Можно ли узнать, сколько изготавливает деталей рабочий за 1 час (Да, нужно его выработку разделить на время его работы)
— Ученик за 1 час? (Да, нужно его выработку разделить на время его работы)
— Зная производительность рабочего и ученика, можно ли ответить на вопрос задачи? (Да, для этого из большего числа вычтем меньшее)
Решение задачи самостоятельно
Самопроверка на мультимедиа
Составление выражения к задаче.
Сравните с выражением в учебнике. В чем разница?
Вывод: Чему мы учились, решая задачу? (ответы учащихся)
РАБОТА НАД ЗАДАНИЯМИ НА РАЗВИТИЕ ЛОГИКИ И СООБРАЗИТЕЛЬНОСТИ
— Для успешного усвоения нового материала мы использовали игру «Что? Где? Когда?», подведем итоги игры.
Что означает сравни выражения в математике 4 класс
Нажмите Ctrl+D , чтобы добавить сайт в избранное.
Страница 34
5. За 3 одинаковых пакета кефира заплатили 87 р., а за 2 одинаковые пачки творога − 72 р. Что дороже: пакет кефира или пачка творога − и на сколько?
6. 1) Вырази в сантиметрах: 6 м; 25 дм; 1 м 8 см; 80 дм.
2) Вырази в часах и минутах: 96 мин; 100 мин; 72 мин.
1) 6 м = 6 * 100 = 600 см
25 дм = 25 * 10 см = 250 см
1 м 8 см = 1 * 100 см + 8 см = 108 см
80 дм = 80 * 10 см = 800 см
2) 96 мин = 60 мин + 36 мин = 1 ч 36 мин
100 мин = 60 мин + 40 мин = 1 ч 40 мин
72 мин = 60 мин + 12 мин = 1 ч 12 мин
7. Верно ли утверждение: «Если периметры прямоугольников равны, то равны и эти прямоугольники?». Приведи примеры.
Нет, утверждение не верно.
Например, периметр прямоугольника равен 40 см, тогда его длина и ширина могут быть следующими:
1) длина = 18, ширина = 2 см:
P = (18 + 2) * 2 = 20 * 2 = 40 (см)
2) длина = 16, ширина = 4 см:
P = (16 + 4) * 2 = 20 * 2 = 40 (см)
3) длина = 18, ширина = 2 см:
P = (14 + 6) * 2 = 20 * 2 = 40 (см)
4) длина = 18, ширина = 2 см:
P = (12 + 8) * 2 = 20 * 2 = 40 (см)
1. Сравни выражения в каждом столбике. Объясни, чем они похожи и чем различаются.
Вычисли значения этих выражений. Сравни полученные результаты.
75 80 40 40
25 * 3 + 5 − 360 : 9 − 3 =37
300 50 200 600
(180 + 120) : 6 + (270 − 70) * 3=650
200 20 470 210
180 + 120 : 6 + 270 − 70 * 3= 260
В каждом столбике в выражениях одинаковые числа, но разный порядок действий, поэтому результаты выражений разные.
2. Расставь скобки в выражении 48 : 4 + 8 * 7 − 5 так, чтобы его значение было равно числу:
1) 28;
2) 23;
3) 135;
4) 8;
5) 40.
4 12 28
2) 48 : (4 + 8) * 7 − 5 = 23
12 20 140
3) (48 : 4 + 8) * 7 − 5 = 135
4 12 2
4) 48 : (4 + 8) * (7 − 5) = 8
12 20 2
5) (48 : 4 + 8) * (7 − 5) = 40
3. Купили 8 м шерстяной ткани, по 140 р. за метр, и 3 м льняной ткани, по 95 р. за метр. Сколько денег израсходовали на всю покупку?
4. От Москвы до Саратова 836 км. Из этих городов навстречу друг другу вышли два поезда. Один из них прошел 362 км, а другой − на 28 км меньше. Какое расстояние осталось между этими поездами?
Равенство и неравенство. Знаки: больше, меньше, равно
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Математические знаки
Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:
Символ меньше (
Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:
Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:
Равенство и неравенство
Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.
Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».
Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.
Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн-формате. Как найти знаки на клавиатуре? Ответ на картинке: