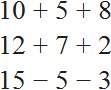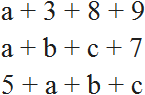Что означает слово выражение в математике
Выражения
Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.
Выражения бывают двух видов: числовые и буквенные.
Числовые выражения состоят из чисел и знаков математических операций. Например, следующие выражения являются числовыми:
Буквенные выражения помимо чисел и знаков операций содержат ещё и буквы. Например, следующие выражения являются буквенными:
Буквы, которые содержатся в буквенных выражениях, называются переменными. Запомните это раз и навсегда! Спросите любого школьника что такое переменная — этот вопрос поставит его в ступор, несмотря на то что он будет решать сложные задачи по математике, не зная что это такое. А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.
Под словом «изучать» мы подразумеваем самостоятельное чтение соответствующей литературы и способность понимать, что там написано. А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.
Поскольку понятие переменной очень важно, остановимся на нём подробнее. Посмотрите внимательно на слово «переменная». Ничего не напоминает? Слово «переменная» происходит от слов «меняться», «изменить», «изменить своё значение». Переменная в математике всегда выражена какой-то буквой. Например, запишем следующее выражение:
Значение переменной a подставляется в исходное выражение.
В результате имеем: 5 + 5 = 10
Конечно, мы рассмотрели простейшее выражение. На практике встречаются более сложные выражения, в которых присутствуют дроби, степени, корни и скобки. Выглядит это устрашающе. На самом деле ничего страшного. Главное понять сам принцип.
Значение переменной x подставляется в выражение x + 10
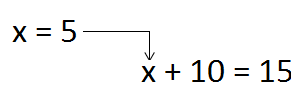
Переменная это своего рода контейнер, где хранится значение. Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.
Имея выражение a + b = c, можно пользоваться им, подставляя вместо переменных a и b любые числа. А переменная c будет получать своё значение автоматически, в зависимости от того, какие числа будут подставлены вместо a и b
Решение:
Значение выражения
Фраза « выполнить действие » означает выполнить одну из операций действия.
Значение выражения — это результат выполнения действий, содержащихся в выражении.
Рассмотрим еще примеры:
Урок математике по теме: «Выражения»
Разделы: Математика
Цели: уточнить понятие «выражение», «числовое выражение», «буквенное выражение». Тренировать способность к составлению сумм и разностей по тексту задач, нахождению значений числовых и буквенных выражений. Формировать способность к использованию скобок для обозначения порядка действий в выражениях; тренировать вычислительные навыки к счёту через 5.
II. Актуализация знаний
— Как называют в математике такую запись? (Выражение)
— Найдите значение выражения. (102)
— Выразите 102 в разных единицах счёта.
— Выразите 102 см в различных единицах длины.
102 см 5 дм 4 см 1 м 2 см 21 дм
___. Определение темы урока
1. Решить примеры, расположить ответы в порядке возрастания, прочитать слово.
— Что такое выражение? Рассмотрите записи на доске и дайте определение?
— На какие две группы можно разделить данные выражения?
— Как можно назвать первую группу выражений? (числовые)
— Вторую группу выражений? (буквенные)
_V. Открытие нового
Составьте к данным карточкам задачи: (устно)
— К каким карточкам вам не удалось составить задачу?
(Вывод: записи, в которых есть знаки сравнения, не являются выражениями)
V. Первичное закрепление (Приложение 1)
1. Определите, являются ли выражениями, данные записи?
Мы зарядку начинаем,
Наши руки разминаем,
Разминаем спину, плечи,
Чтоб сидеть нам было легче.
Дружно прыгаем, прыг-скок!
Кто достанет потолок?
А теперь ходьба на месте.
Громко топаем все вместе.
Мы закончили зарядку,
Возвращаемся к тетрадкам.
3. Запишите выражения к следующим задачам в тетради
Саша заплатил за чай а руб., а за булочку b руб. Сколько всего денег заплатил Саша?
— Что мы записали? (выражения)
— Какие выражения мы записали? (числовое, буквенное)
— В каком выражении мы сможем найти результат? (в числовом)
Вывод: выполнив действие в числовом выражении, найдём значение выражения.
Найдите, какие из данных выражений имеют одинаковое значение?
— Что нового узнали? Какое открытие сделали?
Числовые, буквенные выражения и выражения с переменными: определения, примеры
В математике принято использовать свои обозначения. Запись условий задач с их помощью приводит к появлению так называемых математических выражений. Можно говорить про числовые, буквенные выражения и математические выражения с переменными. Для удобства и одни, и вторые и третьи называются просто выражениями. В этой статье мы дадим определения и по порядку рассмотрим каждый тип математических выражений.
Числовые выражения
Конечно, числовые выражения содержат не только знаки «плюс» и «минус». Они могут включать деление и умножение, содержать скобки, степени, корни, логарифмы и состоять из нескольких действий.
Учитывая все сказанное, дадим определение. Что такое числовое выражение?
Определение. Числовое выражение
Числовым выражением считается только та комбинация, которая составлена с учетом математических правил.
Поясним данное определение.
Во-первых, числа. Математическое выражение может содержать любые числа. Это значит, что в математическом выражении можно встретить:
деление в выражениях может присутствовать как в виде знака, так и в виде дробной черты.
Скобки в числовых выражениях
Согласно определению, числовые выражения могут содержать степени, корни, логарифмы, тригонометрические и обратные тригонометрическим функции. Приведем пример такого числового выражения:
В качестве примера использования в числовых выражениях специальных знаков, можно привести знак модуля.
Буквенные выражения
После знакомства с числовыми выражениями можно вводить понятие буквенных выражений. Интуитивно понятно, что в них вместо чисел используются буквы. Но обо всем по порядку.
Запишем числовое выражение, но вместо одного числа оставим пустой квадратик.
Определение. Буквенное выражение
Выражение, в котором буквы заменяняют некоторые цифры, называется буквенным выражением. Буквенное выражение должно содержать по крайней мере одну букву.
Приведем пример сложного буквенного выражения.
Выражения с переменными
В рассмотренных выше буквенных выражениях буква обозначала какое-то конкретное числовое значение. Величина, которая может принимать ряд различных значений, называется переменной. Выражение с такой величиной, соответственно, называются выражением с переменной.
Определение. Выражения с переменными
Вообще буквенные выражения и выражения с переменными позволяют посмотреть на задачу вне контекста конкретных чисел, то есть более широко. Они широко используются в математическом анализе для формулировок и доказательств.
Внешний вид буквенного выражения не позволяет узнать, являются входящие в него буквы переменными, или нет. Для этого нужно знать условия конкретной задачи, описываемой выражением. Вне контекста ничто не мешает считать входящие в выражение буквы переменными. Таким образом, разница между понятиями «буквенное выражение» и «выражение с переменными» нивелируется.
Числовые выражения и буквенные выражения — правила
При решении примеров и уравнений нужно четко отличать — что такое числовые выражение, а что такое буквенные выражения. Поэтому сегодня пройдем эту тему и посмотрим видео. Итак, выучите правила.
Правила математики о числовых и буквенных выражениях
Число, которое получается в результате выполнения математических операций, входящих в это числовое выражение, называется значением числового выражения.
Числа, которые заменяют букву, называются значениями этой буквы.
Чтобы запомнить правила, давайте обратимся к примерам. Примеры — самый простой наглядный способ запомнить утверждения, приведенные выше.
Примеры числовых выражений
— в левой части этого равенства стоит числовое выражение, а в правой части — значение числового выражения.
— в левой части равенства — числовое выражение, а в правой части — значение числового выражения.
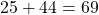
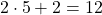
Посмотрите еще примеры числовых выражений:
Примеры буквенных выражений
Примеры буквенных выражений:
Буквенных выражений может быть множество. Для буквенных выражений каждая буква — это определенное число. Или множество разных чисел.
Когда применяются буквенные выражения
Буквенные выражения применяются тогда, когда нам надо, например, ввести формулу для нахождения той или иной величины. Например, вы знаете — что периметр прямоугольника, это сумма всех его сторон. Для периметра в общем виде можно записать буквенное выражение:
, где 
— ширина прямоугольника, а 
— его длина.
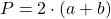
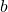
В правой части вы увидели буквенное выражение, значениями букв и — будут числа — значения ширины и длины прямоугольника.
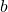
Математические выражения
— это математическое выражение.
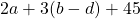
Число перед буквой в математическом выражении — это коэффициент, означающий, что это число умножается на букву, которая может иметь переменное значение.
Буквенные, числовые и математические выражения — необходимо различать, чтобы понимать условия задачи, например, вас могут попросить упростить математическое выражение или попросить найти значение числового выражения. Поэтому необходимо знать — что это такое.
Числовые и буквенные выражения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
14 больше 4
14 > 4
6 + 8 > 2 * 2
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Пример 1. Найдите значение выражения: 5 + x.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.