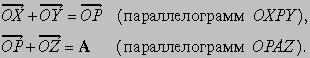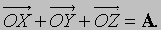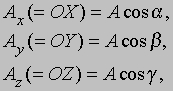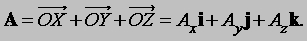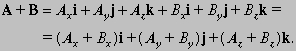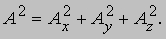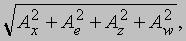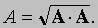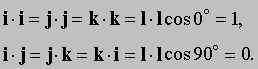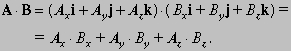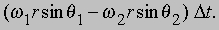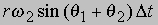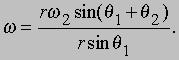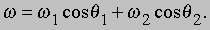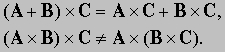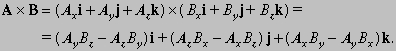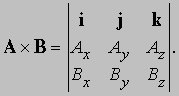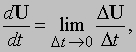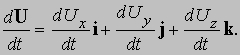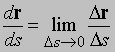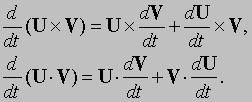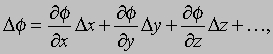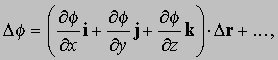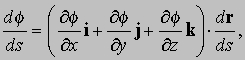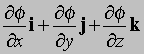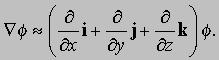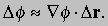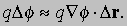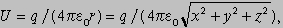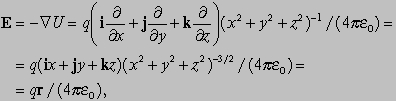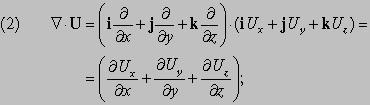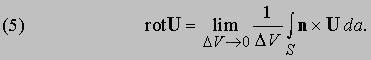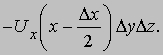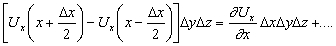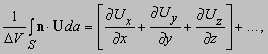Что означает слово скалярная
Скалярный
Смотреть что такое «Скалярный» в других словарях:
скалярный — бесспиновый Словарь русских синонимов. скалярный прил., кол во синонимов: 1 • бесспиновый (2) Словарь синонимов ASIS. В.Н. Тришин … Словарь синонимов
СКАЛЯРНЫЙ — СКАЛЯРНЫЙ, скалярная, скалярное (мат.). прил. к скаляра. Скалярные величины. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
скалярный — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики защита информации EN dot … Справочник технического переводчика
скалярный — скалярный, скалярная, скалярное, скалярные, скалярного, скалярной, скалярного, скалярных, скалярному, скалярной, скалярному, скалярным, скалярный, скалярную, скалярное, скалярные, скалярного, скалярную, скалярное, скалярных, скалярным, скалярной … Формы слов
скалярный — скал ярный … Русский орфографический словарь
скалярный — см. Скаляр … Энциклопедический словарь
скалярный — см. скаляр; ая, ое. С ые величины … Словарь многих выражений
Скалярный процессор — Скалярный процессор это простейший класс микропроцессоров.[1] Скалярный процессор обрабатывает один элемент данных за одну инструкцию (SISD, Single Instruction Single Data), типичными элементами данных могут быть целые или числа с плавающей … Википедия
скалярный магнитный потенциал — Разность скалярных магнитных потенциалов данной точки и другой, определенной, произвольно выбранной. [ГОСТ Р 52002 2003] EN scalar magnetic potential scalar potential of an irrotational magnetic field strength NOTE 1 – The negative of the… … Справочник технического переводчика
Значение слова «скалярный»
СКАЛЯ’РНЫЙ, ая, ое (мат.). Прил. к скаляра. Скалярные величины.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
скаля́рный
1. матем. связанный, соотносящийся по значению с существительным скаляр
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова корениться (глагол), коренится:
Синонимы к слову «скалярный»
Предложения со словом «скалярный»
Сочетаемость слова «скалярный»
Понятия, связанные со словом «скалярный»
Отправить комментарий
Дополнительно
Предложения со словом «скалярный»
Открытие новой частицы очень сильно склонило бы весы в пользу того, что электрослабую симметрию нарушают скалярные поля, а не техницветовое взаимодействие.
Они не связаны с примитивистскими воззрениями на человеческий интеллект как на одномерную скалярную величину.
К скалярным типам относятся стандартные типы и типы, определяемые пользователем.
Синонимы к слову «скалярный»
Сочетаемость слова «скалярный»
Морфология
Правописание
Карта слов и выражений русского языка
Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.
Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.
Сайт оснащён мощной системой поиска с поддержкой русской морфологии.
Скаляры и векторы: что это такое
В физике используется много различных математических величин. Например, ускорение, скорость, сила, работа, мощность и так далее. Ученые делят эти величины на два типа: «скалярные» и «векторные». Что же означают эти типы и чем они отличаются?
Скаляр – это величина, которая описывается только значением. Значение этой величины выражает только число. Примеры скалярных величин: скорость, объем, масса, температура, мощность, энергия, время и т.д. Более о скорости читайте в учебнике по физике за 7 класс В.Г. Баряхтяра.
Вектор – это величина, которая имеет как значение, так и направление. Векторные величины важны при изучении движения. Некоторые примеры векторных величин: сила, скорость, ускорение, перемещение и импульс.
Вектор имеет и направление, и значение, а скаляр имеет только значение. Вы можете сказать, является ли величина вектором, просто если поймете, имеет ли эта величина направление.
Как нарисовать вектор?
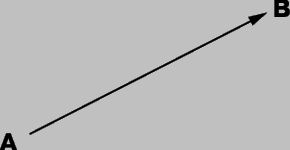
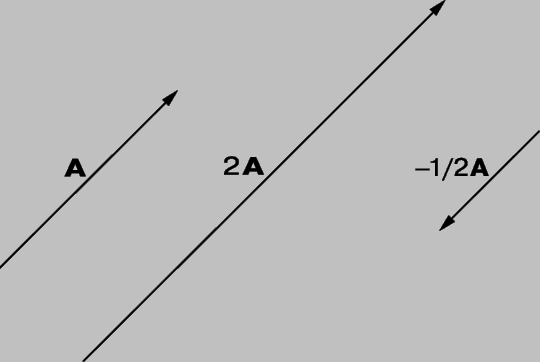
Вектор нарисован в виде стрелки с головой и хвостом. Величину вектора часто описывают длиной стрелки. Стрелка указывает в направлении вектора.
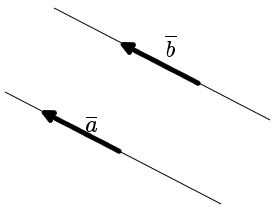
Векторы обычно пишутся в виде жирных букв. Они также могут быть написаны в виде стрелки над буквой.
Пример вопросов: скаляр или вектор?
1) Футболист бежал со скоростью 15 км в час по направлению к концу зоны.
Это вектор, так как он представляет и значение (15 км/ч) и направление (по направлению к концу зоны).
2) Температура помещения составляет 15 градусов по Цельсию.
Это скаляр, направления нет.
3) Автомобиль разогнался на север со скоростью 4 м/с2 (четыре метра в секунду в квадрате).
Это вектор, поскольку он имеет как направление, так и величину. Мы также знаем, что ускорение – это векторная величина.
Словари
Стрелка показывает, что вектор направлен от А в B, а не от B к A.
Два вектора называются равными (или свободными), если их модули и направления совпадают. В механике и физике этим определением, однако, надо пользоваться с осторожностью, так как две равных силы, приложенные к различным точкам тела в общем случае будут приводить к различным результатам. В связи с этим векторы подразделяются на «связанные» или «скользящие», следующим образом: Связанные векторы имеют фиксированные точки приложения. Например, радиус-вектор указывает положение точки относительно некоторого фиксированного начала координат. Связанные векторы считаются равными, если у них совпадают не только модули и направления, но они имеют и общую точку приложения. Скользящими векторами называются равные между собой векторы, расположенные на одной прямой.
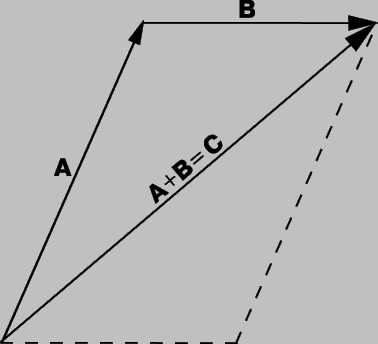
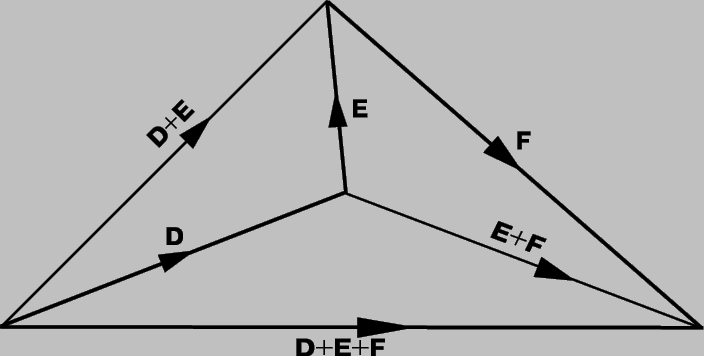
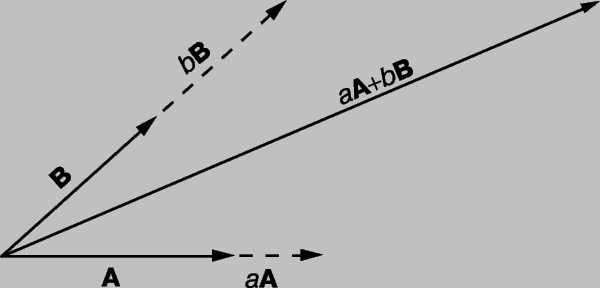
Сложение векторов. Идея сложения векторов возникла из того, что мы можем найти единственный вектор, который оказывает то же воздействие, что и два других вектора вместе. Если для того, чтобы попасть в некоторую точку, нам надо пройти сначала A километров в одном направлении и затем B километров в другом направлении, то мы могли бы достичь нашей конечной точки пройдя C километров в третьем направлении (рис. 2). В этом смысле можно сказать, что
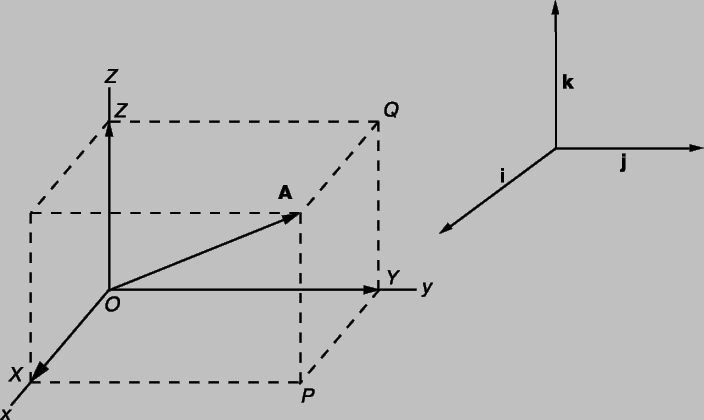
Рис. 5. ВЕКТОРЫ (при использовании декартовых координат) сложенные вместе, дают результирующий вектор А и поэтому называются компонентами A. Координаты в этом случае ориентированы по правилу правой руки (правая декартова система координат).
Можно было бы также сначала сложить и получитьа затем к прибавить Проекции вектора А на три координатные оси, обозначенные Ax, Ay и Az называются «скалярными компонентами» вектора A:
Два вектора равны тогда и только тогда, когда равны их соответствующие скалярные компоненты. Таким образом, A = B тогда и только тогда, когда Ax = Bx, Ay = By, Az = Bz. Два вектора можно сложить, складывая их компоненты:
Кроме того, по теореме Пифагора:
Можно было бы выбрать четыре взаимно перпендикулярных вектора i, j, k и l и определить четырехмерный вектор как величину A = Axi + Ayj + Azk + Awl
Умножение двух векторов. Правило сложения векторов было получено путем изучения поведения величин, представленных векторами. Нет никаких видимых причин, по которым два вектора нельзя было бы каким-либо образом перемножить, однако это умножение будет иметь смысл только в том случае, если можно показать его математическую состоятельность; кроме того, желательно, чтобы произведение имело определенный физический смысл. Существуют два способа умножения векторов, которые соответствуют этим условиям. Результатом одного из них является скаляр, такое произведение называется «скалярным произведением» или «внутренним произведением» двух векторов и записывается AЧB или (A, B). Результатом другого умножения является вектор, называемый «векторным произведением» или «внешним произведением» и записывается A*B или [[A, B]]. Скалярные произведения имеют физический смысл для одного-, двух- или трех измерений, тогда как векторные произведения определены только для трех измерений.
Скалярное произведение можно записать и другим способом. Для этого вспомним, что: A = Ax i + Ayj + Azk. Заметим, что
Поскольку последнее уравнение содержит x, y и z в качестве нижних индексов, уравнение, казалось бы, зависит от выбранной конкретной системы координат. Однако это не так, что видно из определения, которое не зависит от выбранных координатных осей.
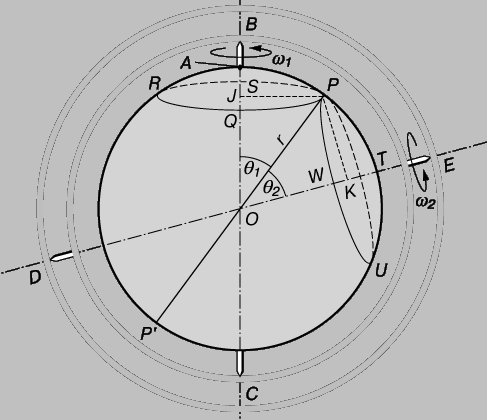
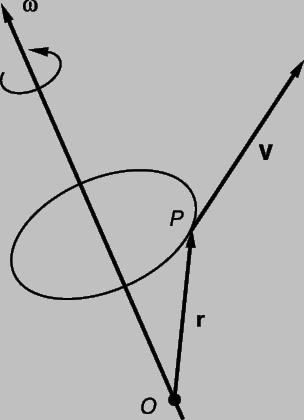
Рис. 7. СФЕРА С ЦЕНТРОМ O, вращается с угловой скоростью w1 внутри кольца BC, которое, в свою очередь, вращается внутри кольца DE с угловой скоростью w2. Сфера вращается с угловой скоростью, равной сумме угловых скоростей и все точки на прямой POP’ находятся в состоянии мгновенного покоя.
Придадим этому телу движение, которое является суммой двух различных угловых скоростей. Это движение довольно трудно представить наглядно, но достаточно очевидно, что тело больше не вращается относительно фиксированной оси. Однако все-таки можно сказать, что оно вращается. Чтобы показать это, выберем некоторую точку P на поверхности тела, которая в рассматриваемый нами момент времени находится на большом круге, соединяющем точки, в которых две оси пересекают поверхность сферы. Опустим перпендикуляры из P на оси. Эти перпендикуляры станут радиусами PJ и PK окружностей PQRS и PTUW соответственно. Проведем прямую POPў, проходящую через центр сферы. Теперь точка P, в рассматриваемый момент времени одновременно перемещается по окружностям, которые соприкасаются в точке P. За малый интервал времени Dt, P перемещается на расстояние
Это расстояние равно нулю, если
В этом случае точка P находится в состоянии мгновенного покоя, и точно также все точки на прямой POP’. Остальная часть сферы будет в движении (окружности, по которым перемещаются другие точки, не касаются, а пересекаются). POPў является, таким образом, мгновенной осью вращения сферы, подобно тому, как колесо, катящееся по дороге в каждый момент времени, вращается относительно своей нижней точки. Чему равна угловая скорость сферы? Выберем для простоты точку A, в которой ось w1 пересекает поверхность. В момент времени, который мы рассматриваем, она перемещается за время Dt на расстояние
по кругу радиуса r sin w1. По определению, угловая скорость
Из этой формулы и соотношения (1) мы получим
Посмотрим, как записывается векторное произведение в терминах компонент и единичных векторов. Прежде всего, для любого вектора A, A * A = AA sin 0 = 0.
Следовательно, в случае единичных векторов, i * i = j * j = k * k = 0 и i * j = k, j * k = i, k * i = j. Тогда,
Это равенство также можно записать в виде определителя:
Заметим, что (A B C) = 0, если все три вектора лежат в одной и той же плоскости или, если А = 0 или (и) В = 0 или (и) С = 0.
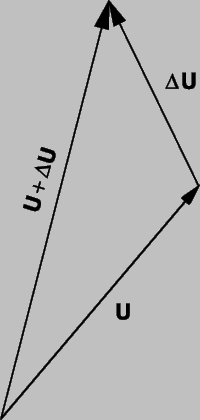
при условии, что такой предел существует. С другой стороны, можно представить U как сумму компонент по трем осям и записать
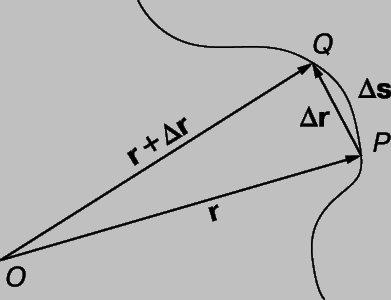
Рис. 10. СЛЕД ЧАСТИЦЫ. Если частица перемещается вдоль кривой на расстояние s, то она пройдет расстояние Ds (от P до Q) в течение малого интервала времени.
есть единичный вектор, касательный к кривой. Это видно из того, что при приближении точки Q к точке P, PQ приближается к касательной и Dr приближается к Ds. Формулы для дифференцирования произведения подобны формулам для дифференцирования произведения скалярных функций; однако, так как векторное произведение антикоммутативно, порядок умножения должен быть сохранен. Поэтому,
Таким образом, мы видим, что, если вектор является функцией одной скалярной переменной, то мы можем представить производную почти также, как в случае скалярной функции.
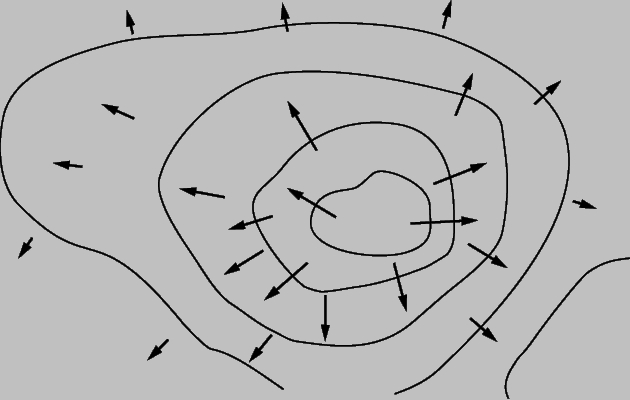
Рис. 11. СКАЛЯРНОЕ ПОЛЕ И ГРАДИЕНТЫ.
В случае трех измерений, контурные линии становятся поверхностями. Малое смещение Dr (= iDx + jDy + kDz) приводит к изменению f, которое записывается как
где точками обозначены члены более высоких порядков. Это выражение можно записать в виде скалярного произведения
Разделим правую и левую части этого равенства на Ds, и пусть Ds стремится к нулю; тогда
— вектор, равный по величине и совпадающий по направлению с максимальной скоростью изменения f относительно координат. Градиент f часто записывается в виде
откуда следует, что E действует в направлении r и его величина равна q/(4pe0r3). Зная скалярное поле, можно определить связанное с ним векторное поле. Также возможно и обратное. С точки зрения математической обработки скалярными полями оперировать легче, чем векторными, так как они задаются одной функцией координат, в то время как векторное поле требует три функции, соответствующие компонентам вектора в трех направлениях. Таким образом, возникает вопрос: дано векторное поле, может ли мы записать связанное с ним скалярное поле?
Используя теорему Тейлора, получим общий вклад от двух граней
Заметим, что DxDyDz = DV. Аналогичным образом можно вычислить вклад от двух других пар граней. Полный интеграл равен
Не все свойства в кристаллах анизотропны. Некоторые свойства, такие как, например, плотность и удельная теплоемкость, изотропны и не зависят от направления. Изотропные свойства описываются скалярными величинами. В то же время, многие свойства, например, теплопроводность (см. ТЕПЛОПРОВОДНОСТЬ), диэлектрическая восприимчивость (см. ДИЭЛЕКТРИЧЕСКАЯ ВОСПРИИМЧИВОСТЬ), магнитная восприимчивость (см. МАГНИТНАЯ ВОСПРИИМЧИВОСТЬ), показатель преломления (см. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ) света и др., существенно зависят от направления, по отношению к которому они определены, и описываются тензорными величинами. Если имеется зависимость свойств от направления, то для их описания, которое в общем случае зависит от ориентации системы координат, используют кристаллофизическую систему координат (см. КРИСТАЛЛОФИЗИЧЕСКАЯ СИСТЕМА КООРДИНАТ).
Наглядное описание анизотропии некоторых свойств дает построение указательных поверхностей (см. ПОВЕРХНОСТЕЙ ТЕОРИЯ), величина радиус-вектора которых соответствует значению измеряемого свойства в данном направлении.
При распространении света в прозрачных кристаллах (кроме кристаллов с кубической решеткой) свет испытывает двойное лучепреломление и поляризуется различно в разных направлениях (см. оптическая анизотропия (см. ОПТИЧЕСКАЯ АНИЗОТРОПИЯ)). Скорость распространения света в кристалле или показатель преломления кристалла различны в различных направлениях. Искусственная оптическая анизотропия возникает в кристаллах и в изотропных средах в результате внешнего воздействия.
Поликристаллы (см. ПОЛИКРИСТАЛЛЫ), состоящие из множества кристаллических зерен (кристаллитов (см. КРИСТАЛЛИТЫ)), ориентированных произвольно, в целом изотропны или почти изотропны. В результате внешних воздействий (механической обработки или отжига) может быть искусственно вызвана анизотропия свойств поликристаллического материала, которая проявляется в том случае, когда в результате обработки в нём создается преимущественная ориентация отдельных кристаллитов в каком-либо направлении (текстура (см. ТЕКСТУРА)). Магнитная анизотропия (см. МАГНИТНАЯ АНИЗОТРОПИЯ) проявляется в поликристаллах, при наличии в них текстуры магнитной (см. ТЕКСТУРА МАГНИТНАЯ) или текстуры кристаллографической.
Анизотропия присуща жидким кристаллам (см. ЖИДКИЕ КРИСТАЛЛЫ), природным и синтетическим полимерным (см. ПОЛИМЕРЫ) веществам. Анизотропия этих веществ, как и кристаллов, в основном определяется их атомным строением и не обязательно требует различия всех свойств во всех направлениях. Наоборот, допустимо закономерное равенство величины какого-либо свойства для некоторых разных направлений.
Анизотропия наблюдается также и в определенных некристаллических веществах, у которых существует естественная или искусственная текстура (древесина и т. п.). В ботанике анизотропией называется способность разных органов одного и того же растения принимать различные положения при одинаковых воздействиях факторов внешней среды.
Введение понятия обратной решетки и обратного пространства, сопряженных с прямой решеткой и прямым пространством, полезно при решении дифракционных задач физики твердого тела, оптики, структурного анализа, электронной микроскопии (см. ЭЛЕКТРОННАЯ МИКРОСКОПИЯ).
Обратная решетка, соответствующая любой прямой решетке, описывающей реальную структуру кристалла, строится следующим образом:
1.Если обычная прямая решетка построена на векторах трансляций a,b,c, то оси обратной к ней решетки a*,b*,c* определяются как векторные произведения:
2.Осевые параметры обратной решетки a*,b*,c* равны обратным величинам межплоскостных расстояний плоских сеток прямой решетки, нормальных к этой оси.
Т. е. вектор обратной решетки H*hkl нормален к каждой плоскости прямой решетки (hkl), а его длина определяется как величина, обратная межплоскостному расстоянию dhkl.
Зоне плоскостей прямой решетки отвечает сетка из точек (узлов) обратной решетки, причем ось зоны прямой решетки нормальна к плоскости сетки обратной решетки. Прямой пространственной решетке из плоскостей hkl отвечает обратная трехмерная решетка из точек [[hkl]]*.
Основные векторы a*,b*,c* обратной решетки определяются также скалярными произведениями:
a*b = a*c = b*c = b*a = c*b = c*a = 0
Физический смысл обратной решетки
Обратная решетка является важным математическим образом, находящим многочисленные применения в геометрической кристаллографии, в теории дифракции и структурном анализе кристаллов, в физике твердого тела.
Например, понятие обратной решетки используется для описания периодического распределения отражающей способности кристалла по отношению к рентгеновским лучам. Отражение рентгеновских лучей от плоскостей структуры кристалла описывается формулой Вульфа-Брэгга (Брэгга-Вульфа условие (см. БРЭГГА-ВУЛЬФА УСЛОВИЕ)), из которого следует, что при постоянной длине волны рентгеновского излучения l большому межплоскостному расстоянию для семейства параллельных отражающих плоскостей d отвечает малый угол падения q, т. е., чем больше межплоскостное расстояние, тем ближе направления отраженных лучей к направлению падающего пучка. Отражения рентгеновских лучей от бесконечно протяженных идеальных кристаллов должны быть точечными.
Каждый узел обратной решетки соответствует возможному отражению от плоскостей прямой решетки кристалла. Направление вектора обратной решетки H*hkl совпадает с направлением отражения от плоскостей hkl в прямой решетке, а n-ый узел обратной решетки в этом ряду отвечает отражению n-го порядка от этих плоскостей.
СКАЛЯРНЫЙ
Смотреть что такое «СКАЛЯРНЫЙ» в других словарях:
скалярный — бесспиновый Словарь русских синонимов. скалярный прил., кол во синонимов: 1 • бесспиновый (2) Словарь синонимов ASIS. В.Н. Тришин … Словарь синонимов
скалярный — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики защита информации EN dot … Справочник технического переводчика
Скалярный — прил. 1. соотн. с сущ. скаляр, связанный с ним 2. Свойственный скаляру, характерный для него. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
скалярный — скалярный, скалярная, скалярное, скалярные, скалярного, скалярной, скалярного, скалярных, скалярному, скалярной, скалярному, скалярным, скалярный, скалярную, скалярное, скалярные, скалярного, скалярную, скалярное, скалярных, скалярным, скалярной … Формы слов
скалярный — скал ярный … Русский орфографический словарь
скалярный — см. Скаляр … Энциклопедический словарь
скалярный — см. скаляр; ая, ое. С ые величины … Словарь многих выражений
Скалярный процессор — Скалярный процессор это простейший класс микропроцессоров.[1] Скалярный процессор обрабатывает один элемент данных за одну инструкцию (SISD, Single Instruction Single Data), типичными элементами данных могут быть целые или числа с плавающей … Википедия
скалярный магнитный потенциал — Разность скалярных магнитных потенциалов данной точки и другой, определенной, произвольно выбранной. [ГОСТ Р 52002 2003] EN scalar magnetic potential scalar potential of an irrotational magnetic field strength NOTE 1 – The negative of the… … Справочник технического переводчика