Что означает слово энтропия
ЭНТРОПИЯ
Полезное
Смотреть что такое «ЭНТРОПИЯ» в других словарях:
ЭНТРОПИЯ — (от греч. entropia поворот, превращение), понятие, впервые введённое в термодинамике для определения меры необратимого рассеяния энергии. Э. широко применяется и в др. областях науки: в статистической физике как мера вероятности осуществления к.… … Физическая энциклопедия
ЭНТРОПИЯ — ЭНТРОПИЯ, показатель случайности или неупорядоченности строения физической системы. В ТЕРМОДИНАМИКЕ энтропия выражает количество тепловой энергии, пригодной для совершения работы: чем энергии меньше, тем выше энтропия. В масштабах Вселенной… … Научно-технический энциклопедический словарь
Энтропия — мера внутренней неупорядоченности информационной системы. Энтропия увеличивается при хаотическом распределении информационных ресурсов и уменьшается при их упорядочении. По английски: Entropy См. также: Информация Финансовый словарь Финам … Финансовый словарь
ЭНТРОПИЯ — [англ. entropy Словарь иностранных слов русского языка
Энтропия — Энтропия ♦ Entropie Свойство состояния изолированной (или принимаемой за таковую) физической системы, характеризуемое количеством самопроизвольного изменения, на которое она способна. Энтропия системы достигает максимума, когда она полностью … Философский словарь Спонвиля
ЭНТРОПИЯ — (от греч. entropia поворот превращение) (обычно обозначается S), функция состояния термодинамической системы, изменение которой dS в равновесном процессе равно отношению количества теплоты dQ, сообщенного системе или отведенного от нее, к… … Большой Энциклопедический словарь
энтропия — беспорядок, разлад Словарь русских синонимов. энтропия сущ., кол во синонимов: 2 • беспорядок (127) • … Словарь синонимов
ЭНТРОПИЯ — (от греч. en в, внутрь и trope поворот, превращение), величина, характеризующая меру связанной энергии (D S), которая в изотермическом процессе не может быть превращена в работу. Она определяется логарифмом термодинамической вероятности и… … Экологический словарь
энтропия — и, ж. entropie f., нем. Entropie <гр. en в, внутрь + trope поворот, превращение. 1. Физическая величина, характеризующая тепловое состояние тела или системы тел и возможные изменения этих состояний. Вычисление энтропии. БАС 1. ||… … Исторический словарь галлицизмов русского языка
ЭНТРОПИЯ — ЭНТРОПИЯ, понятие, вводимое в термодинамике и являющееся как бы мерой необратимости процесса, мерой перехода энергии в такую форму, из к рой она не может самопроизвольно перейти в другие формы. Все мыслимые процессы, протекающие в любой системе,… … Большая медицинская энциклопедия
Энтропия — что это такое: объяснение термина простыми словами
Что такое энтропия? Этим словом можно охарактеризовать и объяснить почти все процессы в жизни человека (физические и химические процессы, а также социальные явления). Но не все люди понимают значение этого термина и уж тем более не все могут объяснить, что это слово значит. Теория сложна для восприятия, но если добавить в неё простые и понятные примеры из жизни, то разобраться с определением этого многогранного термина будет легче. Но обо всём по порядку.
Энтропия: определение и история появления термина
История появления термина
Энтропия как определение состояния системы была введена в 1865 году немецким физиком Рудольфом Клаузиусом, чтобы описать способность теплоты превращаться в другие формы энергии, главным образом в механическую. С помощью этого понятия в термодинамике описывают состояние термодинамических систем. Приращение этой величины связано с поступлением тепла в систему и с температурой, при которой это поступление происходит.
Определение термина из Википедии
Этот термин долгое время использовался только в механической теории тепла (термодинамике), для которой оно вводилось. Но со временем это определение перешло в другие области и теории. Существует несколько определений термина «энтропия».
Википедия даёт краткое определение для нескольких областей, в которых этот термин используется:«Энтропия (от др.-греч. ἐντροπία «поворот»,«превращение») — часто употребляемый в естественных и точных науках термин. В статистической физике характеризует вероятность осуществления какого-либо макроскопического состояния. Помимо физики, этот термин широко используется в математике: теории информации и математической статистике».
Виды энтропий
Этот термин используется в термодинамике, экономике, теории информации и даже в социологии. Что же он определяет в этих областях?
В физической химии (термодинамике)
Основной постулат термодинамики о равновесии: любая изолированная термодинамическая система приходит в равновесное состояние с течением времени и не может из него выйти самопроизвольно. То есть каждая система стремится в равновесное для неё состояние. И если говорить совсем простыми словами, то такое состояние характеризуется беспорядком.
Энтропия — это мера беспорядка. Как определить беспорядок? Один из способов — приписать каждому состоянию число вариантов, которыми это состояние можно реализовать. И чем больше таких способов реализации, тем больше значение энтропии. Чем больше организованно вещество (его структура), тем ниже его неопределённость (хаотичность).
Абсолютное значение энтропии (S абс.) равно изменению имеющейся у вещества или системы энергии во время теплопередачи при данной температуре. Его математическая величина определяется из значения теплопередачи (Q), разделённого на абсолютную температуру (T), при которой происходит процесс: S абс. = Q / T. Это означает, что при передаче большого количества теплоты показатель S абс. увеличится. Тот же эффект будет наблюдаться при теплопередаче в условиях низких температур.
В экономике
В экономике используется такое понятие, как коэффициент энтропии. С помощью этого коэффициента исследуют изменение концентрации рынка и её уровень. Чем выше значение коэффициента, тем выше экономическая неопределённость и, следовательно, вероятность появления монополии снижается. Коэффициент помогает косвенно оценить выгоды, приобретённые фирмой в результате возможной монопольной деятельности или при изменении концентрации рынка.
В статистической физике или теории информации
Информационная энтропия (неопределённость)— это мера непредсказуемости или неопределённости некоторой системы. Эта величина помогает определить степень беспорядочности проводимого эксперимента или события. Чем больше количество состояний, в которых может находиться система, тем больше значение неопределённости. Все процессы упорядочивания системы приводят к появлению информации и снижению информационной неопределённости.
С помощью информационной непредсказуемости можно выявить такую пропускную способность канала, которая обеспечит надёжную передачу информации (в системе закодированных символов). А также можно частично предсказывать ход опыта или события, деля их на составные части и высчитывая значение неопределённости для каждой из них. Такой метод статистической физики помогает выявить вероятность события. С его помощью можно расшифровать закодированный текст, анализируя вероятность появления символов и их показатель энтропии.
Существует такое понятие, как абсолютная энтропия языка. Эта величина выражает максимальное количество информации, которое можно передать в единице этого языка. За единицу в этом случае принимают символ алфавита языка (бит).
В социологии
Здесь энтропия (информационная неопределённость) является характеристикой отклонения социума (системы) или его звеньев от принятого (эталонного) состояния, а проявляется это в снижении эффективности развития и функционирования системы, ухудшении самоорганизации. Простой пример: сотрудники фирмы так сильно загружены работой (выполнением большого количества отчётов), что не успевают заниматься своей основной деятельностью (выполнением проверок). В этом примере мерой нецелесообразного использования руководством рабочих ресурсов будет являться информационная неопределённость.
Энтропия: тезисно и на примерах
Пример 1. Программа Т9. Если в слове будет небольшое количество опечаток, то программа легко распознает слово и предложит его замену. Чем больше опечаток, тем меньше информации о вводимом слове будет у программы. Следовательно, увеличение беспорядка приведёт к увеличению информационной неопределённости и наоборот, чем больше информации, тем меньше неопределённость.
Пример 2. Игральные кости. Выкинуть комбинацию 12 или 2 можно только одним способом: 1 плюс 1 или 6 плюс 6. А максимальным числом способов реализуется число 7 (имеет 6 возможных комбинаций). Непредсказуемость реализации числа семь самая большая в этом случае.
Пример. Н2О (всем известная вода) в своём жидком агрегатном состоянии будет обладать большей энтропией, чем в твёрдом (лёд). Потому что в кристаллическом твёрдом теле каждый атом занимает определённое положение в кристаллической решётке (порядок), а в жидком состоянии у атомов определённых закреплённых положений нет (беспорядок). То есть тело с более жёсткой упорядоченностью атомов имеет более низкое значение энтропии (S). Белый алмаз без примесей обладает самым низким значением S по сравнению с другими кристаллами.
Пример 2. Чем выше порядок на рабочем столе, тем больше информации можно узнать о вещах, которые на нём находятся. В этом случае упорядоченность предметов снижает энтропию системы «рабочий стол».
Пример 3. Информация о классе больше на уроке, чем на перемене. Энтропия на уроке ниже, так как ученики сидят упорядочено (больше информации о местоположении каждого ученика). А на перемене расположение учеников меняется хаотично, что повышает их энтропию.
Пример. При реакции щелочного металла с водой выделяется водород. Водород-это газ. Так как молекулы газа движутся хаотично и имеют высокую энтропию, то рассматриваемая реакция происходит с увеличением её значения. То есть энтропия химической системы станет выше.
В заключение
Если объединить всё вышесказанное, то получится, что энтропия является мерой беспорядка или неопределённости системы и её частей. Интересен тот факт, что всё в природе стремится к максимуму энтропии, а человек — к максимуму информации. И все рассмотренные выше теории направлены на установление баланса между стремлением человека и естественными природными процессами.
Значение слова «энтропия»
1. Физ. Одна из величин, характеризующих тепловое состояние тела или системы тел; мера внутренней неупорядоченности системы.
2. В теории информации — мера неопределенности какого-л. опыта, который может иметь разные исходы.
[От греч. ’εν — в, на и τροπή — поворот, превращение]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Энтропия может интерпретироваться как мера неопределённости (неупорядоченности) некоторой системы, например, какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации. Таким образом, другой интерпретацией энтропии является информационная ёмкость системы. С данной интерпретацией связан тот факт, что создатель понятия энтропии в теории информации (Клод Шеннон) сначала хотел назвать эту величину информацией.
Понятие информационной энтропии применяется как в теории информации и математической статистике, так и в статистической физике (энтропия Гиббса и её упрощённый вариант — энтропия Больцмана). Математический смысл информационной энтропии — это логарифм числа доступных состояний системы (основание логарифма может быть различным, оно определяет единицу измерения энтропии). Такая функция от числа состояний обеспечивает свойство аддитивности энтропии для независимых систем. Причём, если состояния различаются по степени доступности (т. е. не равновероятны), под числом состояний системы нужно понимать их эффективное количество, которое определяется следующим образом. Пусть состояния системы равновероятны и имеют вероятность
Введение в понятие энтропии и ее многоликость
Как может показаться, анализ сигналов и данных — тема достаточно хорошо изученная и уже сотни раз проговоренная. Но есть в ней и некоторые провалы. В последние годы словом «энтропия» бросаются все кому не лень, толком и не понимая, о чем говорят. Хаос — да, беспорядок — да, в термодинамике используется — вроде тоже да, применительно к сигналам — и тут да. Хочется хотя бы немного прояснить этот момент и дать направление тем, кто захочет узнать чуть больше об энтропии. Поговорим об энтропийном анализе данных.
В русскоязычных источниках очень мало литературы на этот счет. А цельное представление вообще получить практически нереально. Благо, моим научным руководителем оказался как раз знаток энтропийного анализа и автор свеженькой монографии [1], где все расписано «от и до». Счастью предела не было, и я решила попробовать донести мысли на этот счет до более широкой аудитории, так что пару выдержек возьму из монографии и дополню своими исследованиями. Может, кому и пригодится.
Итак, начнем с начала. Шенноном в 1963 г. было предложено понятие меры усредненной информативности испытания (непредсказуемости его исходов), которая учитывает вероятность отдельных исходов (до него был еще Хартли, но это опустим). Если энтропию измерять в битах, и взять основание 2, то получим формулу для энтропии Шеннона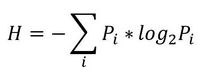 
, где Pi это вероятность наступления i-го исхода.
То есть в этом случае энтропия напрямую связана с «неожиданностью» возникновения события. А отсюда вытекает и его информативность — чем событие более предсказуемо, тем оно менее информативно. Значит и его энтропия будет ниже. Хотя открытым остается вопрос о соотношениях между свойствами информации, свойствами энтропии и свойствами различных ее оценок. Как раз с оценками мы и имеем дело в большинстве случаев. Все, что поддается исследованию — это информативность различных индексов энтропии относительно контролируемых изменений свойств процессов, т.е. по существу, их полезность для решения конкретных прикладных задач.
Энтропия сигнала, описываемого некоторым образом (т.е. детерминированного) стремится к нулю. Для случайных процессов энтропия возрастает тем больше, чем выше уровень «непредсказуемости». Возможно, именно из такой связки трактовок энтропии вероятность->непредсказуемость->информативность и вытекает понятие «хаотичности», хотя оно достаточно неконкретно и расплывчато (что не мешает его популярности). Встречается еще отождествление энтропии и сложности процесса. Но это снова не одно и то же.
Для того, чтобы немного обрисовать области применения энтропии к анализу данных, рассмотрим небольшую прикладную задачку из монографии [1] (которой нет в цифровом виде, и скорей всего не будет).
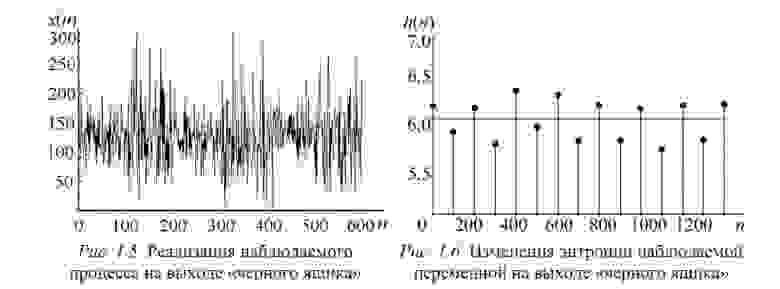
Пусть есть система, которая каждые 100 тактов переключается между несколькими состояниями и порождает сигнал x (рисунок 1.5), характеристики которого изменяются при переходе. Но какие — нам не известно.
Разбив x на реализации по 100 отсчетов можно построить эмпирическую плотность распределения и по ней вычислить значение энтропии Шеннона. Получим значения, «разнесенные» по уровням (рисунок 1.6).
Как можно видеть, переходы между состояниями явно наблюдаются. Но что делать в случае, если время переходов нам не известно? Как оказалось, вычисление скользящим окном может помочь и энтропия так же «разносится» на уровни.В реальном исследовании мы использовали такой эффект для анализа ЭЭГ сигнала (разноцветные картинки про него будут дальше).
Теперь еще про одно занятное свойство энтропии — она позволяет оценить степень связности нескольких процессов. При наличии у них одинаковых источников мы говорим, что процессы связаны (например, если землетрясение фиксируют в разных точках Земли, то основная составляющая сигнала на датчиках общая). В таких случаях обычно применяют корреляционный анализ, однако он хорошо работает только для выявления линейных связей. В случае же нелинейных (порожденных временными задержками, например) предлагаем пользоваться энтропией.
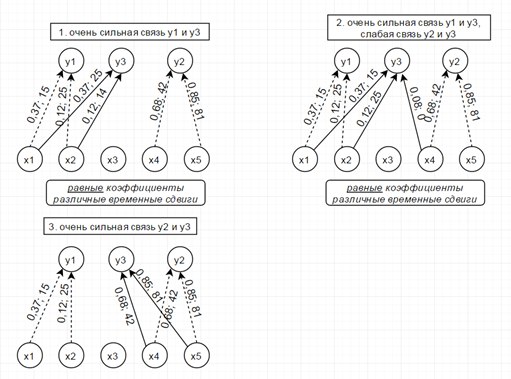
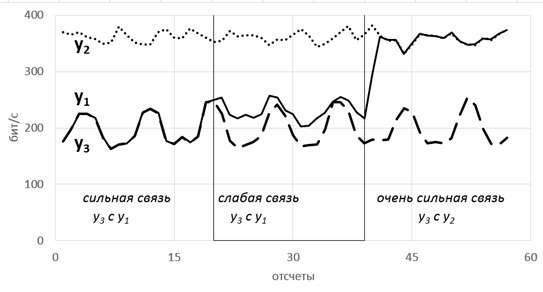
Рассмотрим модель из 5ти скрытых переменных(их энтропия показана на рисунке ниже слева) и 3х наблюдаемых, которые генерируются как линейная сумма скрытых, взятых с временными сдвигами по схеме, показанной ниже справа. Числа-это коэффициенты и временные сдвиги (в отсчетах).
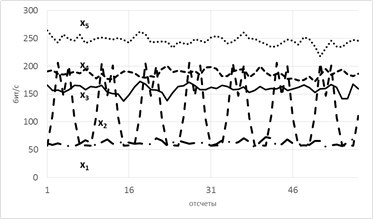
Так вот, фишка в том, что энтропия связных процессов сближается при усилении их связи. Черт побери, как это красиво-то!
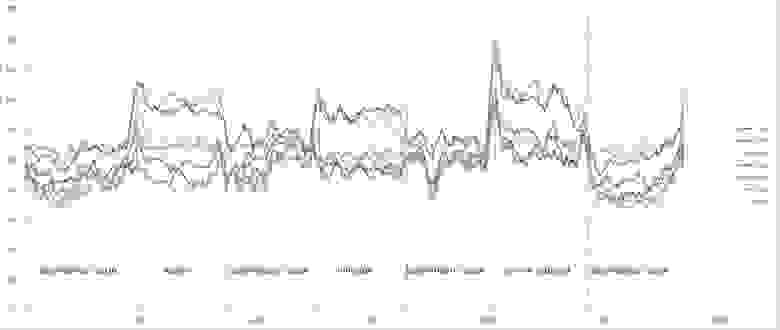
Такие радости позволяют вытащить практически из любых самых странных и хаотичных сигналов (особенно полезно в экономике и аналитике) дополнительные сведения. Мы их вытаскивали из электроэнцефалограммы, считая модную нынче Sample Entropy и вот какие картинки получили.
Можно видеть, что скачки энтропии соответствуют смене этапов эксперимента. На эту тему есть пара статей и уже защищена магистерская, так что если кому будут интересны подробности — с радостью поделюсь. А так по миру по энтропии ЭЭГ ищут уже давно разные вещи — стадии наркоза, сна, болезни Альцгеймера и Паркинсона, эффективность лечения от эпилепсии считают и тд. Но повторюсь-зачастую расчеты ведутся без учета поправочных коэффициентов и это грустно, так как воспроизводимость исследований под большим вопросом (что критично для науки, так то).
Резюмируя, остановлюсь на универсальности энтропийного аппарата и его действительной эффективности, если подходить ко всему с учетом подводных камней. Надеюсь, что после прочтения у вас зародится зерно уважения к великой и могучей силе Энтропии.
Энтропия? Это просто!
Этот пост является вольным переводом ответа, который Mark Eichenlaub дал на вопрос What’s an intuitive way to understand entropy?, заданный на сайте Quora
Энтропия. Пожалуй, это одно из самых сложных для понимания понятий, с которым вы можете встретиться в курсе физики, по крайней мере если говорить о физике классической. Мало кто из выпускников физических факультетов может объяснить, что это такое. Большинство проблем с пониманием энтропии, однако, можно снять, если понять одну вещь. Энтропия качественно отличается от других термодинамических величин: таких как давление, объём или внутренняя энергия, потому что является свойством не системы, а того, как мы эту систему рассматриваем. К сожалению в курсе термодинамики её обычно рассматривают наравне с другими термодинамическими функциями, что усугубляет непонимание.
Так что же такое энтропия?
Энтропия — это то, как много информации вам не известно о системе
Например, если вы спросите меня, где я живу, и я отвечу: в России, то моя энтропия для вас будет высока, всё-таки Россия большая страна. Если же я назову вам свой почтовый индекс: 603081, то моя энтропия для вас понизится, поскольку вы получите больше информации.
Почтовый индекс содержит шесть цифр, то есть я дал вам шесть символов информации. Энтропия вашего знания обо мне понизилась приблизительно на 6 символов. (На самом деле, не совсем, потому что некоторые индексы отвечают большему количеству адресов, а некоторые — меньшему, но мы этим пренебрежём). 
Или рассмотрим другой пример. Пусть у меня есть десять игральных костей (шестигранных), и выбросив их, я вам сообщаю, что их сумма равна 30. Зная только это, вы не можете сказать, какие конкретно цифры на каждой из костей — вам не хватает информации. Эти конкретные цифры на костях в статистической физике называют микросостояниями, а общую сумму (30 в нашем случае) — макросостоянием. Существует 2 930 455 микросостояний, которые отвечают сумме равной 30. Так что энтропия этого макросостояния равна приблизительно 6,5 символам (половинка появляется из-за того, что при нумерации микросостояний по порядку в седьмом разряде вам доступны не все цифры, а только 0, 1 и 2).
А что если бы я вам сказал, что сумма равна 59? Для этого макросостояния существует всего 10 возможных микросостояний, так что его энтропия равна всего лишь одному символу. Как видите, разные макросостояния имеют разные энтропии.
Пусть теперь я вам скажу, что сумма первых пяти костей 13, а сумма остальных пяти — 17, так что общая сумма снова 30. У вас, однако, в этом случае имеется больше информации, поэтому энтропия системы для вас должна упасть. И, действительно, 13 на пяти костях можно получить 420-ю разными способами, а 17 — 780-ю, то есть полное число микросостояний составит всего лишь 420х780 = 327 600. Энтропия такой системы приблизительно на один символ меньше, чем в первом примере.
Мы измеряем энтропию как количество символов, необходимых для записи числа микросостояний. Математически это количество определяется как логарифм, поэтому обозначив энтропию символом S, а число микросостояний символом Ω, мы можем записать:
Это есть ничто иное как формула Больцмана (с точностью до множителя k, который зависит от выбранных единиц измерения) для энтропии. Если макросостоянию отвечают одно микросостояние, его энтропия по этой формуле равна нулю. Если у вас есть две системы, то полная энтропия равна сумме энтропий каждой из этих систем, потому что log(AB) = log A + log B. 
Из приведённого выше описания становится понятно, почему не следует думать об энтропии как о собственном свойстве системы. У системы есть опеделённые внутренняя энергия, импульс, заряд, но у неё нет определённой энтропии: энтропия десяти костей зависит от того, известна вам только их полная сумма, или также и частные суммы пятёрок костей.
Другими словами, энтропия — это то, как мы описываем систему. И это делает её сильно отличной от других величин, с которыми принято работать в физике.
Физический пример: газ под поршнем
Классической системой, которую рассматривают в физике, является газ, находящийся в сосуде под поршнем. Микросостояние газа — это положение и импульс (скорость) каждой его молекулы. Это эквивалентно тому, что вы знаете значение, выпавшее на каждой кости в рассмотренном раньше примере. Макросостояние газа описывается такими величинами как давление, плотность, объём, химический состав. Это как сумма значений, выпавших на костях.
Величины, описывающие макросостояние, могут быть связаны друг с другом через так называемое «уравнение состояния». Именно наличие этой связи позволяет, не зная микросостояний, предсказывать, что будет с нашей системой, если начать её нагревать или перемещать поршень. Для идеального газа уравнение состояния имеет простой вид:
Величины типа давления, температуры и плотности называются усреднёнными, поскольку являются усреднённым проявлением постоянно сменяющих друг друга микросостояний, отвечающих данному макросостоянию (или, вернее, близким к нему макросостояниям). Чтобы узнать в каком микросостоянии находится система, нам надо очень много информации — мы должны знать положение и скорость каждой частицы. Количество этой информации и называется энтропией.
Как меняется энтропия с изменением макросостояния? Это легко понять. Например, если мы немного нагреем газ, то скорость его частиц возрастёт, следовательно, возрастёт и степень нашего незнания об этой скорости, то есть энтропия вырастет. Или, если мы увеличим объём газа, отведя поршень, увеличится степень нашего незнания положения частиц, и энтропия также вырастет.
Твёрдые тела и потенциальная энергия
Если мы рассмотрим вместо газа какое-нибудь твёрдое тело, особенно с упорядоченной структурой, как в кристаллах, например, кусок металла, то его энтропия будет невелика. Почему? Потому что зная положение одного атома в такой структуре, вы знаете и положение всех остальных (они же выстроены в правильную кристаллическую структуру), скорости же атомов невелики, потому что они не могут улететь далеко от своего положения и лишь немного колеблются вокруг положения равновесия. 
Если кусок металла находится в поле тяготения (например, поднят над поверхностью Земли), то потенциальная энергия каждого атома в металле приблизительно равна потенциальной энергии других атомов, и связанная с этой энергией энтропия низка. Это отличает потенциальную энергию от кинетической, которая для теплового движения может сильно меняться от атома к атому.
Если кусок металла, поднятый на некоторую высоту, отпустить, то его потенциальная энергия будет переходить в кинетическую энергию, но энтропия возрастать практически не будет, потому что все атомы будут двигаться приблизительно одинаково. Но когда кусок упадёт на землю, во время удара атомы металла получат случайное направление движения, и энтропия резко увеличится. Кинетическая энергия направленного движения перейдёт в кинетическую энергию теплового движения. Перед ударом мы приблизительно знали, как движется каждый атом, теперь мы эту информацию потеряли.
Понимаем второй закон термодинамики
Второй закон термодинамики утверждает, что энтропия (замкнутой системы) никогда не уменьшается. Мы теперь можем понять, почему: потому что невозможно внезапно получить больше информации о микросостояниях. Как только вы потеряли некую информацию о микросостоянии (как во время удара куска металла об землю), вы не можете вернуть её назад. 
Давайте вернёмся обратно к игральным костям. Вспомним, что макросостояние с суммой 59 имеет очень низкую энтропию, но и получить его не так-то просто. Если бросать кости раз за разом, то будут выпадать те суммы (макросостояния), которым отвечает большее количество микросостояний, то есть будут реализовываться макросостояния с большой энтропией. Самой большой энтропией обладает сумма 35, и именно она и будет выпадать чаще других. Именно об этом и говорит второй закон термодинамики. Любое случайное (неконтролируемое) взаимодействие приводит к росту энтропии, по крайней мере до тех пор, пока она не достигнет своего максимума.
Перемешивание газов
И ещё один пример, чтобы закрепить сказанное. Пусть у нас имеется контейнер, в котором находятся два газа, разделённых расположенной посередине контейнера перегородкой. Назовём молекулы одного газа синими, а другого — красными.
Если открыть перегородку, газы начнут перемешиваться, потому что число микросостояний, в которых газы перемешаны, намного больше, чем микросостояний, в которых они разделены, и все микросостояния, естественно, равновероятны. Когда мы открыли перегородку, для каждой молекулы мы потеряли информацию о том, с какой стороны перегородки она теперь находится. Если молекул было N, то утеряно N бит информации (биты и символы, в данном контексте, это, фактически, одно и тоже, и отличаются только неким постоянным множителем).
Разбираемся с демоном Максвелла
Ну и напоследок рассмотрим решение в рамках нашей парадигмы знаменитого парадокса демона Максвелла. Напомню, что он заключается в следующем. Пусть у нас есть перемешанные газы из синих и красных молекул. Поставим обратно перегородку, проделав в ней небольшое отверстие, в которое посадим воображаемого демона. Его задача — пропускать слева направо только красных, и справа налево только синих. Очевидно, что через некоторое время газы снова будут разделены: все синие молекулы окажутся слева от перегородки, а все красные — справа.
Получается, что наш демон понизил энтропию системы. С демоном ничего не случилось, то есть его энтропия не изменилась, а система у нас была закрытой. Получается, что мы нашли пример, когда второй закон термодинамики не выполняется! Как такое оказалось возможно?
Решается этот парадокс, однако, очень просто. Ведь энтропия — это свойство не системы, а нашего знания об этой системе. Мы с вами знаем о системе мало, поэтому нам и кажется, что её энтропия уменьшается. Но наш демон знает о системе очень много — чтобы разделять молекулы, он должен знать положение и скорость каждой из них (по крайней мере на подлёте к нему). Если он знает о молекулах всё, то с его точки зрения энтропия системы, фактически, равна нулю — у него просто нет недостающей информации о ней. В этом случае энтропия системы как была равна нулю, так и осталась равной нулю, и второй закон термодинамики нигде не нарушился.
Но даже если демон не знает всей информации о микросостоянии системы, ему, как минимум, надо знать цвет подлетающей к нему молекулы, чтобы понять, пропускать её или нет. И если общее число молекул равно N, то демон должен обладать N бит информации о системе — но именно столько информации мы и потеряли, когда открыли перегородку. То есть количество потерянной информации в точности равно количеству информации, которую необходимо получить о системе, чтобы вернуть её в исходное состояние — и это звучит вполне логично, и опять же не противоречит второму закону термодинамики.