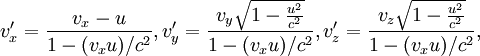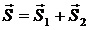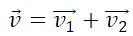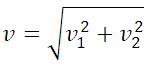Что означает скорость относительна
Вопросы.
1. Что означают следующие утверждения: скорость относительна, траектория движения относительна, путь относителен?
Это означает, что эти величины (скорость, траектория и путь) для движения различаются в зависимости от того, из какой системы отсчета ведется наблюдение.
2. Покажите на примерах, что скорость, траектория движения и пройденный путь являются относительными величинами.
Например, человек стоит неподвижно на поверхности Земли (нет ни скорости, ни траектории, ни пути), однако в это время Земля вращается вокруг своей оси, и следовательно человек, относительно, например центра Земли, движется по определенной траектории (по окружности), перемещается и имеет определенную скорость.
3. Сформулируйте коротко, в чем заключается относительность движения.
Движение тела (скорость, путь, траектория) различны в разных системах отсчета.
4. В чем основное отличие гелиоцентрической системы от геоцентрической?
В гелиоцентрической системе тело отсчета- Солнце, а в геоцентрической- Земля.
5. Объясните смену дня и ночи на Земле в гелиоцентрической системе (см. рис. 18).
В гелиоцентрической системе смена дня и ночи объясняется вращением Земли.
1. Вода в реке движется со скоростью 2 м/с относительно берега. По реке плывёт плот. Какова скорость плота относительно берега? относительно воды в реке?
2. В некоторых случаях скорость тела может быть одинаковой в разных системах отсчёта. Например, поезд движется с одной и той же скоростью в системе отсчета, связанной со зданием вокзала, и в системе отсчёта, связанной с растущим у дороги деревом. Не противоречит ли это утверждению о том, что скорость относительна? Ответ поясните.
3. При каком условии скорость движущегося тела будет одинакова относительно двух систем отсчета?
Если эти системы отсчета неподвижны относительно друг друга.
4. Благодаря суточному вращению Земли человек, сидящий на стуле в своём доме в Москве, движется относительно земной оси со скоростью примерно 900 км/ч. Сравните эту скорость с начальной скоростью пули относительно пистолета, которая равна 250 м/с.
5. Торпедный катер идет вдоль шестидесятой параллели южной широты со скоростью 90 км/ч по отношению к суше. Скорость суточного вращения Земли на этой широте равна 223 м/с. Чему равна в (СИ) и куда направлена скорость катера относительно земной оси, если она движется на восток? на запад?
Относительная скорость
В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух СО.
Обычно выбирают одну из СО за базовую («абсолютную»), другую называют «подвижной» и вводят следующие термины:
Также вводятся понятия соответствующих скоростей и ускорений. Например, переносная скорость — это скорость точки, обусловленная движением подвижной системы отсчёта относительно абсолютной. Другими словами, это скорость точки подвижной системы отсчёта, в данный момент времени совпадающей с материальной точкой.
Оказывается, что при получении связи ускорений в разных системах отсчёта возникает необходимость ввести ещё одно ускорение, обусловленное вращением подвижной системы отсчёта:
В дальнейшем рассмотрении, базовая СО предполагается инерциальной, а на подвижную никаких ограничений не накладывается.
Содержание
Классическая механика
Кинематика сложного движения точки
Скорость
Основные задачи кинематики сложного движения заключаются в установлении зависимостей между кинематическими характеристиками абсолютного и относительного движений точки (или тела) и характеристиками движения подвижной системы отсчета, то есть переносного движения. Для точки эти зависимости являются следующими: абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей, то есть
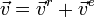
Ускорение
Связь ускорений можно найти путём дифференцирования связи для скоростей, не забывая, что координатные векторы подвижной системы координат также могут зависеть от времени.
Абсолютное ускорение точки равно геометрической сумме трёх ускорений — относительного, переносного и кориолисова, то есть
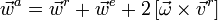
Кинематика сложного движения тела
Для твёрдого тела, когда все составные (то есть относительные и переносные) движения являются поступательными, абсолютное движение также является поступательным со скоростью, равной геометрической сумме скоростей составных движений. Если составные движения тела являются вращательными вокруг осей, пересекающихся в одной точке (как, например, у гироскопа), то результирующее движение также является вращательным вокруг этой точки с мгновенной угловой скоростью, равной геометрической сумме угловых скоростей составных движений. Если же составными движениями тела являются и поступательные, и вращательные, то результирующее движение в общем случае будет слагаться из серии мгновенных винтовых движений.
Рассчитать взаимосвязь скоростей разных точек твёрдого тела в разных системах отсчёта можно с помощью комбинирования формулы сложения скоростей и формулы Эйлера для связи скоростей точек твёрдого тела. Связь ускорений находится простым дифференцированием полученного векторного равенства по времени.
Динамика сложного движения точки
При рассмотрении движения в неинерциальной СО нарушаются первые 2 закона Ньютона. Чтобы обеспечить формальное их выполнение, обычно вводятся дополнительные, фиктивные (не существующие на самом деле), силы инерции: центробежная сила и сила Кориолиса. Выражения для этих сил получаются из связи ускорений (предыдущий раздел).
Релятивистская механика
Скорость
При скоростях, близких к скорости света, преобразования Галилея не являются точно инвариантными и классическая формула сложения скоростей перестаёт выполняться. Вместо этого, инвариантными являются преобразования Лоренца, а связь скоростей в двух инерциальных СО получается следующей:
в предположении, что скорость 
Однако вводится величина — быстрота — которая аддитивна при переходе от одной СО к другой.
Неинерциальные СО
Связь скоростей и ускорений в системах отсчёта, движущихся друг относительно друга ускоренно, является значительно более сложной и определяется локальными свойствами пространства в рассматриваемых точках (зависит от производной тензора Римана).
Литература
См. также
Ссылки
Полезное
Смотреть что такое «Относительная скорость» в других словарях:
относительная скорость — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN relative velocity … Справочник технического переводчика
относительная скорость — santykinis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, išreiškiamas judančiojo kūno ir atskaitos greičių dalmeniu. atitikmenys: angl. non dimensional velocity; relative velocity vok. Geschwindigkeitsverhältnis, n;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
относительная скорость — santykinis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Tekėjimo greičio tam tikrame taške ir tuo pačiu metu išmatuoto pamatinio greičio atitinkamame taške (pvz., greičio ašyje) arba vidutinio ašinio skysčio arba dujų… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
относительная скорость — santykinis greitis statusas T sritis fizika atitikmenys: angl. dimensionless velocity; relative velocity vok. bezogene Geschwindigkeit, f; relative Geschwindigkeit, f rus. относительная скорость, f pranc. vitesse adimensionnelle, f; vitesse… … Fizikos terminų žodynas
СКОРОСТЬ САМОЛЕТА ФАКТИЧЕСКАЯ, ОТНОСИТЕЛЬНАЯ СКОРОСТЬ — скорость передвижения самолета в горизонтальном направлении, исчисляемая относительно земли. По величине и направлению является равнодействующей технической скорости и скорости ветра. С.С.Ф. также называют путевой скоростью. Самойлов К. И.… … Морской словарь
Относительная скорость корабля — скорость корабля относительно движущегося объекта. Испольэустся при решении задач боевого маневрирования кораблей на маневренном планшете и в других случаях. EdwART. Толковый Военно морской Словарь, 2010 … Морской словарь
относительная скорость изделия и преобразователя — Линейная скорость контролируемого изделия относительно системы вихретокового контроля. [Система неразрушающего контроля. Виды (методы) и технология неразрушающего контроля. Термины и определения (справочное пособие). Москва 2003 г.] Тематики виды … Справочник технического переводчика
относительная скорость судна — Скорость движения судна относительно воды [ГОСТ 23634 83] Тематики морская навигация и морская гидрография … Справочник технического переводчика
относительная скорость точки — Скорость точки в относительном движении. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика Обобщающие термины кинематика EN… … Справочник технического переводчика
Относительная скорость.
Относительная скорость – это физическая величина, равная векторной разности скоростей, заданных относительно неподвижной системы отсчета.
При изучении механического движения в первую очередь подчеркивается его относительность. При изучении различных свойств движения тела предполагается, что рассматривается абсолютное движение (т. е. движение, отнесенное к неподвижным осям). Во многих случаях возникает необходимость определить относительное движение, отнесенное к системе отсчета, движущейся по отношению к неподвижным осям.
Относительное движение точки по отношению к подвижной системе отсчета может рассматриваться как абсолютное движение, и обладает всеми свойствами абсолютного движения.
Движение можно рассматривать в разных системах отсчета. Выбор системы отчета диктуется удобством: ее нужно выбрать так, чтобы изучаемое движение и его закономерности выглядели по возможности проще. Для перехода от одной системы отсчета к другой необходимо знать, какие характеристики движения изменяются и каким образом, а какие остаются неизменными.
Исходя из опытов можно утверждать, что при рассмотрении движений, происходящих со скоростями, малыми по сравнению со скоростью света, время неизменно во всех системах отсчета, что означает, что при измерении в любой системе отсчета промежуток времени между двумя событиями одинаков.
Что же касается пространственных характеристик, то положение тела изменяется при переходе к другой системе отсчета, однако при этом не меняется пространственное расположение этих двух событий.
Теперь рассмотрим изменение скорости движения тел при переходе от одной системы отсчета к другой, которая движется относительно первой.
Рассмотрим пример переправы на пароме, движущемся поступательно относительно берегов (относительно земли). Вектор перемещения пассажира относительно берегов обозначим через Δr, а относительно парома – через Δr´. Перемещение парома относительно земли за то же время Δt обозначим через ΔR. В этом случае
Разделим равенство почленно на промежуток времени Δt, в течение которого произошли эти перемещения. Перейдя к пределу Δt >0, получим аналогичное соотношение для скоростей:
Из формулы (2) следует, что относительная скорость двух тел одинакова во всех системах отсчета. При переходе к новой системе отсчета к скорости каждого тела прибавляется один и тот же вектор V скорости системы отсчета. Поэтому разность векторов скоростей тел υ – υ´ не изменяется. Относительная скорость тел абсолютна.
Абсолютная, относительная и переносная скорости
В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух СО.
Обычно выбирают одну из СО за базовую («абсолютную»), другую называют «подвижной» и вводят следующие термины:
Также вводятся понятия соответствующих скоростей и ускорений. Например, переносная скорость — это скорость точки, обусловленная движением подвижной системы отсчёта относительно абсолютной. Другими словами, это скорость точки подвижной системы отсчёта, в данный момент времени совпадающей с материальной точкой.
Оказывается, что при получении связи ускорений в разных системах отсчёта возникает необходимость ввести ещё одно ускорение, обусловленное вращением подвижной системы отсчёта:
В дальнейшем рассмотрении, базовая СО предполагается инерциальной, а на подвижную никаких ограничений не накладывается.
Содержание
Классическая механика
Кинематика сложного движения точки
Скорость
Основные задачи кинематики сложного движения заключаются в установлении зависимостей между кинематическими характеристиками абсолютного и относительного движений точки (или тела) и характеристиками движения подвижной системы отсчета, то есть переносного движения. Для точки эти зависимости являются следующими: абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей, то есть
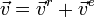
Ускорение
Связь ускорений можно найти путём дифференцирования связи для скоростей, не забывая, что координатные векторы подвижной системы координат также могут зависеть от времени.
Абсолютное ускорение точки равно геометрической сумме трёх ускорений — относительного, переносного и кориолисова, то есть
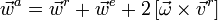
Кинематика сложного движения тела
Для твёрдого тела, когда все составные (то есть относительные и переносные) движения являются поступательными, абсолютное движение также является поступательным со скоростью, равной геометрической сумме скоростей составных движений. Если составные движения тела являются вращательными вокруг осей, пересекающихся в одной точке (как, например, у гироскопа), то результирующее движение также является вращательным вокруг этой точки с мгновенной угловой скоростью, равной геометрической сумме угловых скоростей составных движений. Если же составными движениями тела являются и поступательные, и вращательные, то результирующее движение в общем случае будет слагаться из серии мгновенных винтовых движений.
Рассчитать взаимосвязь скоростей разных точек твёрдого тела в разных системах отсчёта можно с помощью комбинирования формулы сложения скоростей и формулы Эйлера для связи скоростей точек твёрдого тела. Связь ускорений находится простым дифференцированием полученного векторного равенства по времени.
Динамика сложного движения точки
При рассмотрении движения в неинерциальной СО нарушаются первые 2 закона Ньютона. Чтобы обеспечить формальное их выполнение, обычно вводятся дополнительные, фиктивные (не существующие на самом деле), силы инерции: центробежная сила и сила Кориолиса. Выражения для этих сил получаются из связи ускорений (предыдущий раздел).
Релятивистская механика
Скорость
При скоростях, близких к скорости света, преобразования Галилея не являются точно инвариантными и классическая формула сложения скоростей перестаёт выполняться. Вместо этого, инвариантными являются преобразования Лоренца, а связь скоростей в двух инерциальных СО получается следующей:
в предположении, что скорость 
Однако вводится величина — быстрота — которая аддитивна при переходе от одной СО к другой.
Неинерциальные СО
Связь скоростей и ускорений в системах отсчёта, движущихся друг относительно друга ускоренно, является значительно более сложной и определяется локальными свойствами пространства в рассматриваемых точках (зависит от производной тензора Римана).
Как сказал.
Вопросы к экзамену
Для всех групп технического профиля

Я учу детей тому, как надо учиться
Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.
Урок 02. (дополнительный материал). Относительность механического движения
Относительность механического движения.
Механическое движение относительно. Движение одного и того же тела относительно разных тел оказывается различным.
Например, автомобиль движется по дороге. В автомобиле находятся люди. Люди движутся вместе с автомобилем по дороге. То есть люди перемещаются в пространстве относительно дороги. Но относительно самого автомобиля люди не движутся. В этом проявляетсяотносительность механического движения.
Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета. Покой тоже относителен. Например, пассажир в покоящемся поезде смотрит на проходящий мимо поезд и не понимает, какой поезд движется, пока не посмотрит на небо или землю.
Все тела во Вселенной движутся, поэтому не существует тел, которые находятся в абсолютном покое. По той же причине определить движется тело или нет, можно только относительно какого-либо другого тела.
Например, автомобиль движется по дороге. Дорога находится на планете Земля. Дорога неподвижна. Поэтому можно измерить скорость автомобиля относительно неподвижной дороги. Но дорога неподвижна относительно Земли. Однако сама Земля вращается вокруг Солнца. Следовательно, дорога вместе с автомобилем также вращается вокруг Солнца. Следовательно, автомобиль совершает не только поступательное движение, но и вращательное (относительно Солнца). А вот относительно Земли автомобиль совершает только поступательное движение. В этом проявляется относительность механического движения.
Движение одного и того же тела может выглядеть по-разному с точки зрения различных наблюдателей. Скорость, направление движения и вид траектории тела будут различными для различных наблюдателей. Без указания тела отсчета разговор о движении является бессмысленным. Например, сидящий пассажир в поезде покоится относительно вагона, но движется вместе с вагоном относительно платформы вокзала.
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными.
Галилей показал, что в условиях Земли практически справедлив закон инерции. Согласно этому закону действие на тело сил проявляется в изменениях скорости; для поддержания же движения с неизменной по величине и направлению скоростью не требуется присутствия сил. Системы отсчета, в которых выполняется закон инерции, стали называть инерциальные системы отсчета (ИСО).
Системы, которые вращаются или ускоряются, неинерциальные.
Землю нельзя считать вполне ИСО: она вращается, но для большинства наших целей системы отсчета, связанные с Землей, в достаточно хорошем приближении можно принять за инерциальные. Система отсчета, движущаяся равномерно и прямолинейно относительно ИСО, также инерциальная.
Г. Галилей и И. Ньютон глубоко осознавали то, что мы сегодня называем принципом относительности, согласно которому механические законы физики должны быть одинаковыми во всех ИСО при одинаковых начальных условиях.
Из этого следует: ни одна ИСО ничем не отличается от другой системы отсчета. Все ИСО эквивалентны с точки зрения механических явлений.
Принцип относительности Галилея исходит из некоторых допущений, которые опираются на наш повседневный опыт. В классической механике пространство и время считаются абсолютными. Предполагается, что длина тел одинакова в любой системе отсчета и что время в различных системах отсчета течет одинаково. Предполагается, что масса тела, а также все силы остаются неизменными при переходе из одной ИСО в другую.
В справедливости принципа относительности нас убеждает повседневный опыт, например в равномерно движущемся поезде или самолете тела движутся так же, как и на Земле.
Не существует эксперимента, с помощью которого можно было бы установить, какая система отсчета действительно покоится, а какая движется. Нет систем отсчета в состоянии абсолютного покоя.
Если на движущейся тележке подбросить монету вертикально вверх, то в системе отсчета, связанной с тележкой, будет изменяться только координата ОУ.
В системе отсчета, связанной с Землей, изменяются координаты ОУ и ОХ.
Следовательно, положение тел и их скорости в разных системах отсчета различны.
Рассмотрим движение одного и того же тела относительно двух разных систем отсчета: неподвижной и движущейся.
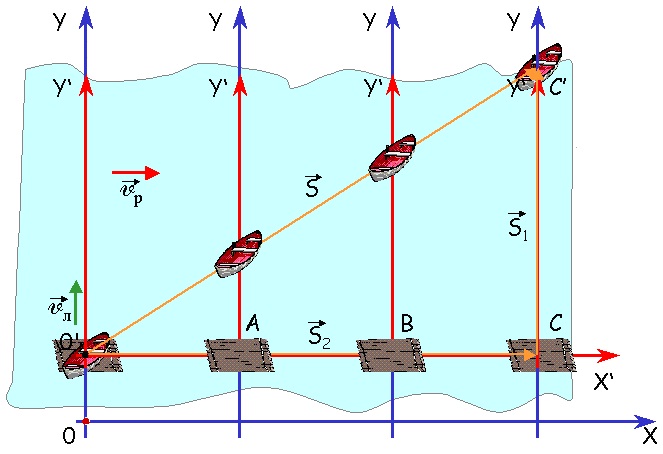
Лодка пересекает реку перпендикулярно течению реки двигаясь с некоторой скоростью относительно воды. За движением лодки следят 2 наблюдателя: один неподвижный на берегу, другой на плоту, плывущем по течению. Относительно воды плот неподвижен, а по отношению к берегу он движется со скоростью течения.
С каждым наблюдателем свяжем систему координат.
X0Y – неподвижная система координат.
X’0’Y’ – подвижная система координат.
S – перемещение лодки относительно неподвижной СО.
S1 – перемещение лодки относительно подвижной СО
S2 – перемещение подвижной системы отсчета относительно неподвижной СО.
По закону сложения векторов
Скорость получим разделив S на t:
v – скорость тела относительно неподвижной СО
v1 – скорость тела относительно подвижной СО
v2 – скорость подвижной системы отсчета относительно неподвижной СО
Эта формула выражает классический закон сложения скоростей: скорость тела относительно неподвижной СО равна геометрической сумме скорости тела относительно подвижной СО и скорости подвижной СО относительно неподвижной СО.
В скалярном виде формула будет иметь вид:
Впервые эту формулу получил Галилей.
Принцип относительности Галилея: все инерциальные системы отсчета равноправны; ход времени, масса, ускорение и сила в них записываются одинаково.
Скачать презентацию с Яндекса