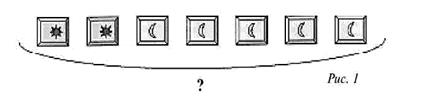
Что означает схематический рисунок задачи
Задача (условие, вопрос, схема, выражение, ответ). 1-й класс
Класс: 1
I. Организационный момент.
— Ребята, сегодня на уроке мы отправляемся с вами путешествовать в страну Математики и нас будет сопровождать Великий Математик. Математика – это точная наука, требующая хороших знаний, чёткого выполнения всех арифметических действий.
— Какие действия мы с вами уже знаем? (Сложение и вычитание.)
— Во 2 классе мы познакомимся с умножением и делением.
— Сегодня на уроке мы будем заниматься наблюдениями, открывать математические закономерности, изучать новый материал.
1) Путешествовать мы с вами отправляемся на поезде, но прежде, чем наш поезд тронется, мы должны получить билеты. Для этого разделимся на команды и поиграем в игру «Кто быстрее?»
(Учащиеся выходят к доске и дописывают нужные числа.)
III ряд – 3 команда.
2) А теперь надо узнать № поезда. Для этого решим цепочку примеров:
Проверка (у каждого учащегося цифры, ответ показывает каждый с места).
(На доске картинка с зайчиком).
— Зайчик тоже хочет отправиться с нами путешествовать, но он не знает номер поезда, ему достался трудный пример. Он записан под цепочкой.
(Учащиеся записывают пример в тетради и решают.)
— Что вы заметили? (В примере выполнены те же действия, что и в цепочке. Значит ответ будет такой же 9.)
Значит Зайка едет в нашем поезде – берём его с собой.
Наш поезд отправился, давайте сосчитаем:
— Сколько пассажиров в каждом вагоне?
| 9-6 | 3 | 4+5 | 9 | 8-4 | 4 |
| 3+3 | 6 | 7-5 | 2 | 3+4 | 7 |
— Запишите их в порядке возрастания и вы отгадаете слово.
(На доске все картинки перемешаны, выходит ученик и располагает их в порядке возрастания.)
— Какое слово получилось? (Дети отвечают хором.)
IV. Знакомство с новым материалом.
Тема сегодняшнего урока: Задача.
Наш поезд делает I остановку в лесу. Рассмотрите иллюстрацию. Составьте задачу про детей.
«Мальчик и девочка пошли в лес за грибами. Мальчик нашёл 2 гриба, а девочка 4.Сколько всего грибов нашли дети?»
— Правильно. Без чего нет задачи? (Без вопроса.)
— В задаче всегда о чём-то спрашивается, без вопроса нет задачи. Это нужно хорошо понять и запомнить.
— Задачу можно разбить на 2 части:
(На доске постепенно открываются плакаты: условие, вопрос, схема, выражение, решение, ответ.)
— Давайте повторим условие нашей задачи, вопрос.
— А теперь запишем в тетради: Задача.
— Ниже запишите выражение: 4 + 2.
— Найдите его значение: 4 + 2 = 6(гр.)
— Полученное равенство называют решением задачи, а значение выражения 6 грибов – ответом задачи.
Ответ: 6 грибов. (На доске записан образец записи.)
— Разобраться в этом помогает рисунок, но если числа большие то делать рисунок неудобно – слишком много предметов надо рисовать. На помощь приходит схема-отрезок, разбитый на части. Разбивая отрезок на части, мы получаем те же самые соотношения между частью и целым, что и при разбиении совокупностей предметов.
— Какой мы делаем вывод? (Наглядно представить содержание задачи можно сопоставив целое всему отрезку, а части – частям отрезка.)
— Что такое целое? (Отрезок.)
— Что обозначает весь отрезок? (Число грибов, собранных детьми.)
— Что такое части? (Части отрезка.)
— Что обозначают части отрезка? (Грибы, собранные мальчиком и девочкой.)
— Что показывает знак вопроса? (Находят целое.)
— Каким действием решаем задачу? (Сложением.)
— Почему? (Находим целое.)
1) Следующая остановка нашего поезда «Поиграй-ка».
— А сейчас мы с вами немного поиграем.
— Великий Математик прислал конверты с задачами.
— Каждой группе нужно определить, что относится к условию, вопросу, найти схему, записать выражение, решение, назвать ответ.
А) Условие. Во дворе играли 6 ребят. Двое ушли домой.
Вопрос. Сколько ребят осталось во дворе?
На доске выражение: 6 – 2.
Б) Условие. В хоре пело 4 мальчика и 6 девочек.
Вопрос. Сколько детей пело в хоре?
В) Условие. Из клетки улетело сначала 2 попугая, а потом ещё 3.
Вопрос. Сколько попугаев улетело из клетки?
2) Наш поезд продолжает путешествие.
— Следующая остановка: «Объясни-ка».
— Откройте учебник с. 44 урок 23 № 2.
— Что нужно сделать? (Соотнести записи в рамках с соответствующими терминами.)
— Назовите условие, вопрос, выражение, решение.
— Что обозначает весь отрезок? (Число конфет у девочки.)
— Его части? (Число конфет, которые она подарила и число конфет, которые у неё остались.)
— Почему задача решается вычитанием? (Ищем части.)
— Как найти часть? (Из целого вычитаем другую часть.)
3) Перейдём к №3. Составьте задачу по рисунку.
На столе лежали яблоки в 2-х вазах. В 1 вазе – 5 яблок, во 2 – 2 яблока.
— Сколько всего яблок лежало в двух вазах?
— Назовите условие, вопрос, выражение, решение.
— Что обозначает весь отрезок? (Все яблоки, лежащие на 1 и 2 вазе.)
— Его части? (1 ваза с яблоками, 2 – с яблоками.)
— Почему задача решается сложением? (Находим целое.)
4) Путешествие наше продолжается, но нам надо забрать багаж в камере хранения ( №5).
Расшифруем записи – код ячеек.
— Что нужно выполнить? (Составить выражение с заданным числовым значением и дорисовать картинки.) Выполните самостоятельно.
Проверка (плакат на доске).
— Наше путешествие подходит к концу.
— И в последнем задании Великий Математик зашифровал слово.
— Если вы правильно выполните действие и сосчитаете, то узнаете слово (умница).
— Великий Математик считает, что вы все умницы, так как хорошо работали на уроке и правильно отвечали на все вопросы, и выполнили все задания.
— Что нового узнали, чем занимались на уроке?
Конспект урока математики для 2 класса «Решение задач с составлением схематического рисунка или чертежа»
пробного урока математики
ТЕМА «Решение задач с составлением схематического чертежа или схематического рисунка»
Содержательная: Закреплять умение решать задачи в два действия с составлением схематических рисунков и чертежей
Деятельностная: способствовать формированию УУД.
Личностные:
— Способствовать овладению основами логического и алгоритмического мышления, математической речи.
— Способствовать появлению учебно-познавательного интереса к учебному материалу.
— Способствовать развития способности к оценке своей учебной деятельности.
— Развивать умение принимать и сохранять учебную задачу
— Развивать умение учитывать установленные правила в планировании и контроле способа решения
— Развивать умения учитывать выделенные учителем ориентиры действия в новом учебном материале в сотрудничестве с учителем
— Развивать умение проявлять познавательную инициативу в учебном сотрудничестве
— Развивать умение строить сообщения в устной и письменной форме
— Развивать умение использовать знаково-символические средства для решения задач
постановки и решения проблемы:
— Развивать умение владения рядом общих приёмов решения задач
— Развивать умение адекватно использовать речевые средства для решения различных коммуникативных задач
— Развивать умение применять математические знания и представления для решения учебных задач
— Развивать умение самостоятельно составлять выражения
— Развивать умение выполнять письменно арифметические действия с числами
— Развивать умение проводить проверку правильности вычислений (с помощью обратного действия, прикидки и оценки результата действия и др.)
— Развивать умение оценивать правильность хода решения и реальность ответа на вопрос задачи
Виды моделей, применяемых при решении текстовых задач, и методика работы с ними
Модель – это мостик от абстрактного к конкретному, по которому движется мысль школьника.
Форма моделей может быть различной: модельная схема, знаковая модель, графическая, образная.
В методической литературе по математике различают:
1. Предметную наглядность: предметы окружающей обстановки (карандаши, тетради, счётные палочки, жёлуди); модели предметов; картинки с изображением предметов: фруктов, овощей, животных;
2. Графическую (условную) наглядность: схематические рисунки, чертежи [13].
Модели, используемые в начальной школе на уроках математики, бывают разные. Их можно разделить на схематизированные и знаковые по видам средств, используемых для их построения. Схематизированные модели, в свою очередь, делятся на вещественные и графические в зависимости от того, какое действие они обеспечивают. Вещественные (или предметные) модели текстовых задач обеспечивают физическое действие с предметами. Они могут строиться из каких-либо предметов (пуговиц, спичек, бумажных полосок), они могут быть представлены разного рода инсценировками сюжета задач. К этому виду моделей причисляют и мысленное воссоздание реальной ситуации, описанной в задаче, в виде представлений.
Графические модели используются, как правило, для обобщенного, схематического воссоздания ситуации задачи. К графическим следует отнести следующие виды моделей:
· схематический чертёж (или просто схема).
Целесообразно начинать систематически обучать учащихся моделированию текстовых задач уже в 1-м классе. Первоначально необходимо знакомить учеников с различными видами моделей, применимых к задаче.
Рисунок.Знакомство с моделированием, следует начинать в 1-м классе именно с этой модели по ряду причин:
— в задачах идет речь о доступных ребенку предметах;
— моторика руки у учащихся развита слабо, и рисование является развивающим упражнением;
Использование рисунка особенно результативно, когда в задаче идет речь о реальных и простых в изображении предметах (кубиках, платочках, яблоках).
«У Тани было несколько значков. Она подарила 2 значка подруге, и у нее осталось 5 значков. Сколько значков было у Тани?».
Рисунок в виде реальных предметов выглядит следующим образом:
Модель в виде реальных предметов
Если предметы заменить геометрическими фигурами, то рисунок принимает такой вид: (рис. 2)
Рис.2 Схематический рисунок
В целях формирования осознанного подхода к составлению и применению моделей в виде рисунка в учебнике к этой задаче даются следующие задания:
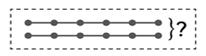
Выбери схему и реши задачу по рис. 3.
Сначала уехало 7 машин, а потом — 3 машины. Сколько машин уехало?
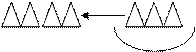 | |
 |  |
 |
Рис. 3 Схематический рисунок
Эти задания способствуют формированию навыка составления и анализа моделей[7].
Света сначала нарисовала 5 домиков, а потомещё 3 домика. Сколько стало домиков на рисунке у Светы?[7].
Схематический рисунок может выглядеть так: (рис.4 )
 |  |  |  |  |  |
 | |||||
 |  |  | |||
 |  |  |  |  |
Рис.4 Схематическая иллюстрация к задаче на нахождение суммы.
На схеме в верхнем ряду стрелка помогает детям зафиксировать на бумаге образ того действия, которое предполагается выполнить с фигурами (придвинуть). На схеме во втором ряду стрелки не показаны, и дети оперируют мысленным образом того, как перемещаются фигуры при объединении выделенных групп. Схема второго ряда очень полезна, поскольку готовит детей к работе со схематическим чертежом[ 13].
Не следует, считая рисунок самой простой моделью, пренебрегать им в 3-м и 4-м классах; используя при решении трудных задач более сложные модели, необходимо давать возможность ученику вернуться к рисунку, если у него возникает такая потребность.
Краткая запись.С моделью данного вида можно работать уже в конце 1-го класса, когда навык письма у учащихся сформирован настолько, что на каллиграфическое письмо уходит не слишком много времени.
Рассмотрим это на примере следующей задачи:
В кувшине было 10 стаканов воды. Выпили8 стаканов. Сколько стаканов воды осталось в кувшине?[7].
Краткая запись к задаче на уменьшение на несколько единиц.
Опорное слово «выпили» говорит младшему школьнику о том, что количество стаканов с водой в кувшине уменьшилось, следовательно, надо производить вычитание (10-8=2)
Избежать ошибок подобного рода и помогает прием моделирования: ребенку предлагается составить модель другого вида, позволяющую проследить за количественными изменениями в задаче (чертеж, схему, рисунок, «дерево рассуждений»).
В пенале 2 ручки. Сколько ручек в трёх таких пеналах? Учебник 2 ч.с.94
| Ручек в пенале (шт.) | Количество пеналов (шт.) | Всего ручек (шт.) |
| ? |
Рис. 5. Таблица при решении простых задач на умножение и деление
Рассуждай так: Для решения задачи нужно по два взять три раза. Значит, нужно 2 умножить на 3.
Чертеж
Чертеж- условное изображение предметов, взаимосвязей между ними и взаимоотношения величин с помощью отрезков и с соблюдением определенного масштаба. В обучении поиску решения задач используют специфические чертежи, на которых взаимосвязи и взаимоотношения передаются приблизительно, без точного соблюдения масштаба (их часто называют схематическими или схема). Работа со схематическим чертежом начинается после того, как дети познакомились с понятием «отрезок».
Чертеж как вид модели целесообразно применять при следующих условиях:
— наличие у детей определенных навыков вычерчивания отрезков заданной длины;
— удобные числовые данные в задаче, позволяющие начертить отрезок заданной длины.
Ученики должны усвоить поэтапное выполнение чертежа.
Катя купила 5 тетрадей в клетку и столько же тетрадей в линейку. Сколько всего тетрадей купила Катя? [6].
Рис. 6. Схематический чертёж к задаче, выполненный на пунктирной основе
Со 2 класса предполагается переход к работе со схематическим чертежом, который условно, без поэлементного соответствия, передаёт численность представляемых в задаче множеств.
В автопарке стояло 36 автомобилей, а автобусов на 20 больше. Сколько автобусов стояло в автопарке?[13]
Схема к задаче с большими числовыми данными может выглядеть так, так изображено на рис. 7.


 |
 |
 |
Учим первоклассника составлять схемы предложения
Как научить ребенка изображать предложения схематично? Родители, чьи дети учатся в начальных классах, знают, без помощи взрослого, маленькому ученику, иногда, не обойтись. Проблема в том, что папа с мамой, за годы после школы и сами забыли все правила. Ничего страшного! Необходимую тему можно вспомнить или выучить заново. В статье мы расскажем, как научить ребенка составлять схемы простых и сложных предложений самостоятельно.
Начало занятия
В первую очередь, следует определить, что обозначается словом – предложение. Это связанные логически и интонацией несколько слов, в числе которых, обязательно присутствует грамматическая основа из подлежащего (объект) и сказуемого (его действие). Рассмотрим данное правило на примере.
Предложение: папа смотрит телевизор. Грамматическая основа: «папа» (слово отвечает на вопрос – «Кто?»), «смотрит» (обозначение действия, слово отвечает на вопрос – «Что делает?»). «Телевизор» в данном предложении будет второстепенным членом.
Простые схемы
Самые простые схемы предложения обозначают его как цельную единицу текста, знак препинания в конце – указание на цель высказывания (повествовательное, вопросительное, восклицательное). Вертикальная черточка обозначает заглавную букву.
Дети играют I_________.
Мама поливает цветы I__________.
После того, как ребенок освоит изображение таких схем, задание можно усложнить. Теперь, предстоит обозначить нижним подчеркиванием каждое слово.
Ребята катаются на велосипедах. I__ __ _ __.
Мы едем в отпуск! I_ __ _ __!
Ты умеешь бросать мяч в корзину? I_ __ __ __ _ __?
Длинным подчеркиванием обозначаются слова, коротким – междометия, предлоги, местоимения.
Орфограммы в схемах
Прежде чем приступить к обучению ребенка самостоятельно изображать схемы предложения, ему следует рассказать о некоторых правилах написания предложений. Первое – географические названия, населенные пункты, клички животных, имена, отчества и фамилии людей пишутся с большой буквы. В схемах предложений обозначаются вертикальной черточкой.
Марина и Олеся поедут зимой к дедушке. I__ _ I__ __ __ _ __.
Олегу очень нравится мороженое. I__ __ __ __.
Следующее понятие, с которым можно познакомить ребенка – диалог, где речь каждого из его участников пишется с новой строчки, а перед первым словом ставится «тире». Его же прописывают и в схеме предложения, если это необходимо.
– Кто выпил весь компот? – I__ __ __ __?
Построение схемы пошагово
Как максимально понятно объяснить ребенку порядок составления схемы предложения? Донести самое главное правило – горизонтальных черточек в схеме, должно быть столько же, сколько и слов, вертикальных – сколько слов, написанных с большой буквы.
Порядок составления схемы, которому следует приучить ребенка:
После последовательного выполнения всех пунктов, приступить к составлению схемы.
Полезные советы взрослому
Первое время, чтобы ребенку было легче, можно положить перед ним несколько примеров, глядя на которые он по подобию составит свои схемы.
Первые предложения должны быть простыми, состоящими из 2-4 слов. Если ребенок испытывает затруднения с подсчетом количества слов, при их произношении можно хлопать в ладоши. Пусть малыш считает хлопки.
Особое внимание следует уделить союзам, предлогам, частицам. Объяснить ребенку, что вот такие слова следует изображать короткой черточкой, и сразу же, составить несколько схем. Показать наглядно, как это должно выглядеть.
Для чего ребенку нужен навык схематического изображения предложений
Обучение ребенка составлению схем, важно. В процессе, дети учатся быстрее читать и ловить смысл текста. Им становится значительно легче находить границы предложений, различать вопросительные, повествовательные или восклицательные. Практика работы с текстами, в целом, развивает ребенка, расширяет словарный запас, улучшает память.
Моделировать задачу в виде схемы, рисунка, краткой записи, подбирать опорную схему для решения задачи.
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Сквозная тема: Путешествие
Раздел долгосрочного плана: Равенства неравенства. Уравнения.
ФИО учителя: Подкопова Г.М.
Цели обучения, которые достигаются на данном уроке: 1.5.1.1. Моделировать задачу в виде схемы, рисунка, краткой записи, подбирать опорную схему для решения задачи.
Все учащиеся смогут: моделировать задачу в виде схемы, рисунка, краткой записи, подбирать опорную схему для решения задачи.
Большинство учащихся смогут анализировать условие задачи, выбирать оптимальный
Некоторые учащиеся смогут делать выводы о рациональной записи условия задачи и моделировать задачу по опорной схеме, рисунку, краткой записи.
Учащиеся могут: отвечать на вопросы и обосновывают свой ответ используя ключевые слова и фразы при моделировании задач.
Ключевые слова и фразы : задача, условие, вопрос, решение, ответ, схема, рисунок, краткая запись.
Стиль языка, подходящий для диалога/письма в классе:
Вопросы для обсуждения: Что такое задача? Из каких частей состоит задача? Как можно записать условие задачи по разному?
1.4.1.1. наглядно изображать объединение двух множеств и удаление части множества.
Эмоциональный настрой – создание коллаборативной среды
Приветствие учащихся. Повернитесь друг другу и пожелайте мысленно удачи.
Деление учащихся по группам.
Звучит музыка каждый ребенок заранее получил геометрическую фигуру пока звучит музыка дети должны найти свою фигуру в группе и занять место. Класс разделён на 6 групп.
Девиз нашего урока « Не стыдно не знать,
Сегодня мы с вами отправляемся в математическое путешествие. Как называются люди, которые путешествуют?
Для чего люди отправляются в путешествие?
« Тут затеи и задачи
Игры, шутки всё для вас
Пожелаем всем удачи
. 1. В снег упал Серёжа,
Сколько на снегу ребят?
Красиво вышила Татьяна
Две лилии и два тюльпана.
Какие чудные цветы!
А сколько их? Нам скажешь ты.
В шкафу на полке пять книг
Я прочитала две из них
Осталось сколько книг читать?
Вы это можете узнать?.
Ребята, что мы с вами сейчас решали?
Чем отличаются примеры от задачи?
Давайте узнаем, как произносится слово задача на казахском языке и английском. Один ученик произносит, остальные учащиеся произносят хором.
Определите цель нашего урока. Чему будем учиться на уроке?
Вывод: Сегодня на уроке мы будем учиться моделировать задачу в виде схемы, рисунка и краткой записи.
Чтобы правильно научиться решать задачи, что мы должны знать о задаче?
3. Составление алгоритма решения задачи. (Работа в группе) Дифференциация по результату выполненного задания.
Наше путешествие продолжается. Скажите, как по другому можно назвать путешественников.
Туристы всегда стремятся узнать больше информации, сегодня мы с вами находимся в математической стране и попробуем составить алгоритм решения задачи.
Г.Ф. Каждая группа должна составить алгоритм решения задачи.
Перед вами лежат полоски со словами – восстановите последовательность решения задачи.
1. Прочитать задачу
2. Найти вопрос задачи.
3. Написать краткое условие.
4. Решить задачу.
5. Написать ответ.
Формативное оценивание – по шаблону.
Первичное закрепление – соедини линиями части задачи.
Красных – 5 шаров Ответ
Зелёных – 3 шара Условие
Ответ: всего 8 шаров.
Проверка – взаимопроверка по шаблону.
Я понял но затрудняюсь – зелёным
Я не понял – красным.
Докажите, что именно в такой последовательности нужно решать задачу.
Мы с вами продолжаем изучать ключевые слова нашего урока – произнесите слова «Условие, вопрос, решение, ответ» на трёх языках русском, казахском, английском. Произношение слов хором, по группам.
Карточки с геометрическими фигурами.
Карточки со словами
1. Прочитать задачу
2. Найти вопрос задачи.
3. Написать краткое условие.
4. Решить задачу.
5. Написать ответ.
1 Правильно различает части задачи
Мы продолжаем наше путешествие.
Исследование. Групповая форма работы. Продолжаем работать в группе. Рассмотрите записанные задачи, обсудите в группе в чем сходства и различия. Какой можно сделать вывод.
По одному ученику от группы выходят и делятся своей информацией.
Формативное оценивание – «Три хлопка»
Выводы: Запись условия задачи можно выполнить по разному – в виде схемы, рисунка, краткой записи.
Первичное закрепление – индивидуальная работа соедини запись условия задачи с видом (схема, рисунок, краткая запись)с
11 + 6 = 17 Краткая запись
Проверка – самопроверка по шаблону
Я понял но затрудняюсь – зелёным
Я не понял – красным.
2. Соедини условие задачи с видом (схема, рисунок, краткая запись)
Я разобрался с разными видами записи условия – голубым
Я определяю только рисунок – зелёным
Я определяю только схему – жёлтым.
Я не разобрался в записи условия задачи – красным.
Задача: Туристы посетили 10 музеев и 3 парка. Сколько всего достопримечательностей посетили туристы?
При решении задачи пользуйтесь алгоритмом решения задачи.
Я понял но затрудняюсь – зелёным
Я не понял – красным.
2. Соедини условие задачи с видом (схема, рисунок, краткая запись)
Я разобрался с разными видами записи условия – голубым
Я определяю только рисунок – зелёным
Я определяю только схему – жёлтым.
Я не разобрался в записи условия задачи – красным.
3. Составление и решение задачи
Я решил 3 задачи – голубой
Я решил только – 2 задачи – зелёный
3. Я решил 1 задачу – красный.
Мы с вами познакомились еще с новыми словами как они звучат на трёх языках. Произнесите слова «Схема, рисунок, краткая запись»
3. Аргументируют свой ответ.
Карточки с задачей.
1 Правильно соединил условие задачи с видами (схема, рисунок, краткая запись)
2. Умеет аргументировать выполнение задания.
1 запись условия задачи
2 правильно поставлен вопрос
3 правильно выбрано действие для решения задачи.
4 правильно записан ответ
Рефлексия. «Схема успеха» Наше путешествие подошло к концу. Если вам было интересно на уроке и вы справились со всеми заданиями – приклейте голубой самолёт к солнышку, если было интересно и вы затруднялись с каким то заданием – приклейте зелёный самолёт к тучке с солнышком, если вам было интересно но вы не справились с заданием – то приклейте красный самолёт к тучке.
Ученики выбирают самолет по цвету и приклеивают на схему успеха
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?
Здоровье и соблюдение техники безопасности
Дифференциация может быть выражена в подборе заданий, в ожидаемом результате от конкретного ученика, в оказании индивидуальной поддержки учащемуся, в подборе учебного материала и ресурсов с учетом индивидуальных способностей учащихся (Теория множественного интеллекта по Гарднеру).
Дифференциация может быть использована на любом этапе
Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока.
Используемые физминутки и активные виды деятельности.
Пункты, применяемые из Правил техники безопасности на данном уроке.
урока с учетом рационального использования времени.
Были ли цели урока/цели обучения реалистичными?
Все ли учащиеся достигли ЦО?
Если нет, то почему?
Правильно ли проведена дифференциация на уроке?
Выдержаны ли были временные этапы урока?
Какие отступления были от плана урока и почему?
Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки.
Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?
Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)?
Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках