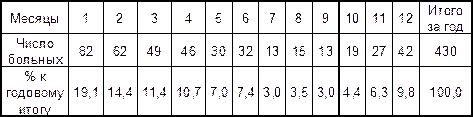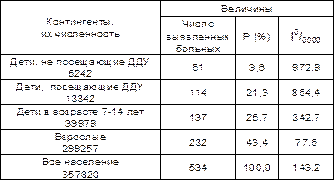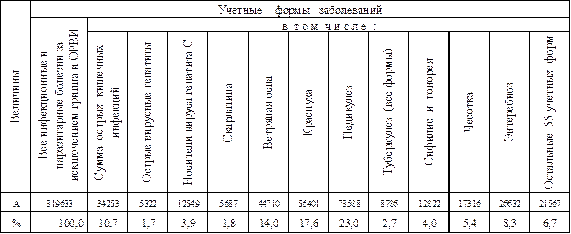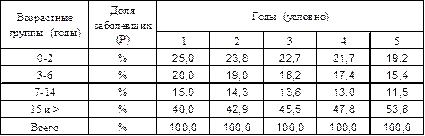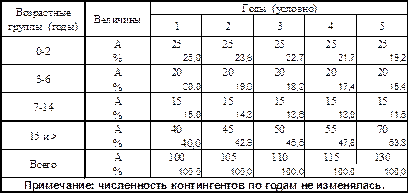Что означает экстенсивный показатель
Что означает экстенсивный показатель
В процессе эпидемиологического анализа приходится постоянно оперировать также такими статистическими понятиями, как интенсивные и экстенсивные показатели, средние величины и т.д.
Экстенсивный показатель — это доля определенного варианта того признака, который в той или другой разновидности встречается во всех изучаемых случаях. Обычно он выражается в процентах. Экстенсивные показатели взаимозависимы: если в изучаемой группе психически больных (то, что все составляющие группу лица, психически больные — это признак) случаи шизофрении (диагноз — вариант этого признака) составляют 60 %, то на прочие заболевания придется 40 %.
Интенсивный показатель — это мера частоты определенного признака среди тех случаев, в которых этот признак может быть, а может и не быть. Если мы говорим, что распространенность шизофрении среди населения составляет 1 на 1000, то это интенсивный показатель. Он не зависит от других интенсивных показателей: среди населения может быть сколько угодно больных с другими заболеваниями и здоровых, а показатель распространенности шизофрении при этом не изменится.
Использование экстенсивных и интенсивных показателей зависит от задачи исследования. Если нужно решить, как распределить имеющийся коечный фонд для лечения пациентов разного возраста, то нужны экстенсивные показатели, характеризующие возраст больных: сколько процентов среди них составляют дети, лица среднего и лица пожилого возраста. Если же нас интересует, у кого чаще отмечаются психические расстройства — у детей, людей старшего возраста или у стариков, то экстенсивные показатели ничего не дадут: может случиться, что процент пожилых среди пациентов будет очень высоким, потому что в городе значительную часть населения составляют пожилые люди. Для решения этой задачи необходимы интенсивные показатели: сколько приходится больных на 1000 детского населения, на 1000 пожилого населения и на 1000 населения среднего возраста. Тогда сравнение будет адекватным.
Средняя величина (точнее среднее арифметическое) — одно из самых частых понятий, используемых в эпидемиологических исследованиях. Говорят о средней длительности пребывания больного на койке, среднем числе посещений диспансера в день, средней длительности ремиссий и о множестве других средних величин. Не останавливаясь на вычислении среднего арифметического, рассмотрим вопрос о содержательном значении средней величины.
Если утверждается, что, например, средний рост мужчины составляет 175 см, то смысл этого утверждения очень глубок. Существует фундаментальная причина, определяющая именно эту величину: рост — генетически обусловленный признак (именно поэтому мужчины в среднем выше женщин).
Врач сталкивается с множеством подобных явлений. Это размеры и масса живых существ, длительность пребывания больного на койке, количество препарата, нужное для лечения определенного расстройства, и во всех этих случаях средняя величина имеет совершенно четкий смысл: она указывает, что причина явления определяет именно эту характеризующую его величину, а все отклонения от нее определяются влиянием случайностей.
Статистическое распределение количественных характеристик отдельных случаев, относящихся к подобному явлению, всегда бывает так называемым гауссовским, или нормальным (рис. 25). Если желательно использовать для характеристики каких-то данных их среднюю величину, следует проверить, соответствует ли распределение этих данных нормальному; если да, то применение средней величины оправдано, она имеет смысл: именно средняя величина определяется основной причиной изучаемого явления. Однако часто при такой проверке обнаруживается, что данные распределяются иначе. В частности, длительность многих психопатологических состояний имеет экспоненциальное (а не нормальное) распределение, которое свидетельствует о том, что количественная характеристика каждого отдельного наблюдения случайна. Средняя величина в таких случаях не имеет содержания. Именно поэтому в ядерной физике не употребляют понятие «среднее время распада ядер» радиоактивного вещества, а говорят о «периоде полураспада», т.е. о времени, за которое распадается половина всех имеющихся ядер. Подобно этому не следует характеризовать средними величинами и длительность психопатологических синдромов.
При эпидемиологических исследованиях часто сравнивают две выборки (или более). При этом может возникнуть проблема их несопоставимости (например, выборки очень различаются по возрастной структуре, что мешает решить поставленную задачу). В таких случаях помогает метод стандартизации данных, описанный, например, Н.А.Вигдорчиком (1945). Смысл этого метода заключается в том, что искусственно устраняется различие между выборками по всем факторам, кроме изучаемого.
С проблемой проверки достоверности статистических различий эпидемиолог сталкивается всякий раз, когда сравнивает два показателя. Если в каждой из срав ниваемых групп не меньше 20 наблюдений, то на этот вопрос отвечает критерий Стьюдента (Т), вычисляемый по известной формуле:
где p 1 и р2 — сравниваемые показатели, n 1и n2 — численность подвыборок.
Достоверным считается то различие, при котором разность между показателями в определенное число раз больше, чем сумма их ошибок. Это число (Т) определяется тем уровнем надежности, который принят в данном исследовании. При таком условии число Т (критерий Стьюдента) должно быть больше 2. Если это так, то различие считается достоверным: можно быть уверенным, что по крайней мере в 95 из 100 любых аналогичных выборок различие окажется примерно таким же (плюс-минус ошибка).
Если сравниваемые группы маленькие (содержат менее 20 наблюдений), то для проверки достоверности различий между ними метод Стьюдента непригоден. Поэтому обычно стараются избегать слишком маленьких групп. Однако это не всегда возможно, и тогда приходится применять так называемый точный метод Фишера. С его помощью вычисляется не условный коэффициент (как при методе Стьюдента), а величина вероятности, что полученный результат случаен. Если эта вероятность меньше 0,025, то различие признается достоверным.
Различия, которые при проверке оказываются статистически недостоверными, могут тем не менее иметь большое значение. Особенно часто это случается, когда сравнивается ряд показателей, характеризующих, например, динамику какого-либо процесса. Важным может оказаться не определение достоверности различий соседних показателей, а закономерность их изменений. Закономерные изменения всегда говорят о чем-то важном, независимо от того, достоверны ли различия между составляющими ее показателями.
Анализируя изменения показателей, постоянно приходится думать, не закономерны ли эти изменения. С распространением компьютерных технологий обработки полученных данных эта задача стала простой. Например, программный пакет » Microsoft Excel » решает ее автоматически, подбирая к экспериментальным данным линию тренда (определяя тенденцию их изменений) и указывая, насколько точно она их описывает.
Одной из главных методологических проблем при организации эпидемиологических исследований в психиатрии является идентификация больных. Последняя при эпидемиологическом обследовании отличается от обычной клинической диагностики. Массовость материала заставляет эпидемиолога опираться на стандартные диагностические критерии. Это требование вступает в очевидное противоречие со стремлением иметь как можно более добротный в клиническом отношении материал. При компромиссном решении, которое приходится принимать, неизбежно в жертву приносится либо стандартность диагностики, либо степень ее клинической фундированности. Зарубежные авторы, как правило, жертвуют последним, отдавая безусловный приоритет обеспечению сопоставимости материала разных исследователей. Поэтому они уже много лет используют формальные диагностические инструменты (опросники, шкалы, структурированные интервью и т.п.).
Клинико-эпидемиологический метод, описанный ранее и на протяжении многих лет используемый в отделе эпидемиологии Научного центра психического здоровья РАМП, характеризуется тем, что исследователи, применяя его, отдают предпочтение клинической добротности материала, а это затрудняет сравнение полученных результатов с данными зарубежных авторов. Изложенные трудности идентификации больных могут быть, по-видимому, отчасти преодолены использованием МКБ-10, поскольку эта международная диагностическая система снабжена подробной методикой постановки диагноза, обеспечивающей полную стандартность диагностики, без изменения клинического содержания диагноза.
Экстенсивные показатели
Экстенсивные показатели, или показатели структуры (т.е. внутреннего строения, устройства) изучаемого явления оценивают величину какой-либо структурной части ко всему явлению. Измеренные части явления называют долямиилиудельными весами, оценивающими вклад каждой части в общее явление.
Размерность экстенсивных показателей (т.е. долей, удельных весов, вкладов) принципиально может быть любой, но чаще всего ее выражают в процентах, реже – в долях единицы, принимая целое, соответственно за 100 или за 1.
При изучении структуры заболеваемости общая формула расчета:
где:
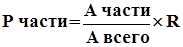
Р части – экстенсивный показатель заболеваемости, оценивающий удельный вес какой-либо структурной части заболеваемости (заболевших) в известном суммарном числе заболевших;
А части – число случаев болезни, относящееся к какой-либо структурной части заболевших (группе больных);
А всего – (основание показателя) – число случаев болезни, отражающее всю, существующую в пределах данной структуры, заболеваемость, т.е. суммарное число больных во всех группах составляющих данную структуру;
R – размерность показателя – проценты (%).
При изучении структуры заболеваемости используются различные группировочные признаки, позволяющие делить всех больных на группы (структурные части) и создавать, таким образом, различные структурные распределения определенного, часто одного и того же, суммарного числа больных. Ниже приведены некоторые примеры различных структурных распределений.
Так, использование в качестве группировочного признака диагноза заболевания позволяет изучить структуру заболеваемости по нозологическим формам болезней.
В 2002 г. в Москве было выявлено 2712880 больных, относящихся к 75 нозологическим формам инфекционных и паразитарных болезней. В том числе, 2300430 больных острыми респираторными болезнями (ОРВИ), 92817 больных гриппом, 34253 больных различными острыми кишечными инфекциями (ОКИ), 56401 больных краснухой и так далее.
Исходя из этих данных доля (удельный вес, вклад) заболевших каждой из этих болезней в общей сумме всех больных всеми инфекционными и паразитарными болезнями составил:
Р больных ОРВИ= (2300430/2712880)´100 = 84,8%
Р больных гриппом = (92817/2712880)´100 = 3,4%
Р больных ОКИ = (34253/2712880)´100 = 1,3%
Р больных краснухой = (56401/2712880)´100 = 2,1%
Не менее важным является анализ структурных распределений составленных с учетом времени возникновения случаев болезни.
Например, данные табл..2 позволяют оценить вклад заболевших в каждом месяце в общую сумму заболевших за год.
. 
Табл. 2 Помесячное распределение больных скарлатиной среди всего населения г. В. в 2000 году
Использование для группировки различных индивидуальных признаков, позволяет создавать и изучать разнообразные структурные распределения больных, например, по полу, возрасту, профессиям, особенностям клинического течения болезни и т.д.
В 2000 году в Москве было выявлено 272954 больных 73 инфекционными и паразитарными болезнями. Среди них было 696835 больных детей в возрасте до 7 лет, 649395 больных детей в возрасте 7 – 14 лет и 1381724 больных взрослых. Соответственно удельный вес каждой указанной возрастной группы составил:
Р больных детей до 7 лет=(696865/272954)´100 = 25,6%
Р больных детей 7 –14 лет = (649395/272954)´100 =23,8%
Р больных взрослых = (1381724/272954)´100 = 50,8%
Экстенсивный показатель, оценивающий долю какой-либо части заболеваемости, должен иметь все те же названия, что и интенсивный показатель, т.е. название болезни, время, место возникновения случая болезни, обозначение индивидуальных признаков больных. Кроме того, обязательнодолжна быть обозначена (названа) общая сумма заболевших, принимаемая за А всего,т.е. сумма заболевших составляющая данное структурное распределение.
Абсолютно бесполезной является следующая информация – «в Москве в 2002 г удельный вес заболевших скарлатиной детей до 14 лет составил 5,2%».
Бесполезность этой информации связана с отсутствием обозначения той суммы больных, для которой определялась доля детей больных скарлатиной. Доля таких больных (а всего было выявлено 5687 детей до 14 больных скарлатиной) будет существенно различаться в зависимости от того, какие цифры принимаются за суммарное количество больных. Например, возможны следующие варианты:
· доля больных скарлатиной детей рассчитанная исходя из суммарного числа больных детей до 14 лет в Москве в 2002 г. независимо от наименования инфекционной болезни составит – Р=(5687/1341569)´100=0,42%;
· доля больных скарлатиной детей, рассчитанная исходя из общего числа всех (независимо от возраста) больных инфекционными и паразитарными болезнями в Москве в 2002 г. составит – Р=(5687/2712880)´100=0,21%;
· доля больных скарлатиной детей, рассчитанная исходя из суммарного числа больных 6 детскими инфекциями (коклюшем, скарлатиной, натуральной оспой, корью, краснухой и эпидемическим паротитом) составит – Р=(5687/108638)´100=5,2%
Таким образом, информация, указанная в начале примера, относится только к последнему структурному варианту оценки удельного веса детей до 14 лет заболевших скарлатиной в Москве в 2002 г.
В отличие от интенсивных показателей, экстенсивные показатели заболеваемости можно объединить, но при условии, если они относятся к одному структурному распределению.
По данным предыдущего примера доли больных всеми инфекционными и паразитарными болезнями в Москве в 2000г. составили для детей:
Величина экстенсивных показателей при сравнимом качестве выявления, диагностики и учета больных, зависит от влияния большего количества факторов, чем величина интенсивных показателей.
Значение отдельного интенсивного показателя, отражающего частоту заболеваний в отдельной группе населения, определяется только:
· риском заболеть (заразиться и заболеть) представителей исключительно данной группы;
· численностью данной группы населения.
Следовательно, изменение интенсивного показателя одной группы населения никак не сказывается на величине интенсивных показателей в других группах.
Значение отдельного экстенсивного показателя, отражающего долю заболевших отдельной группы населения в общей сумме больных, принятых за 100%, определяется:
· риском заболеть (заразиться и заболеть) характерным не только для данной группы, но и других групп населения;
· численностью каждой группы населения, входящей в данное распределение заболевших.
Именно поэтому величина экстенсивных показателей и их изменение может зависеть с равной вероятностью, как от факторов присущих отдельной группе населения, так и факторов влияющих на число заболевших в других группах.
При трактовке результатов изучения структуры заболеваемости, к сожалению, допускаются типичные и серьезные ошибки.
Во избежание такой ошибки необходимо помнить и понимать формулы расчетов интенсивных и экстенсивных показателей заболеваемости. Числители этих показателей одинаковы – абсолютное число больных в определенных группах населения. Знаменатели этих показателей разные. У интенсивного показателя знаменатель – численность определенной группы населения, у экстенсивного показателя знаменатель – суммарное число больных в изучаемых группах. Вследствие этого величины интенсивного и экстенсивного показателя заболеваемости какой-либо группы населения статистически абсолютно независимы друг от друга. Так, например, при одной и той же частоте заболеваний в разных группах населения, доли заболевших, относящихся к этим группам, могут существенно различаться, причем тем больше, чем больше различается численность отдельных групп населения. Сравнительно незначительный риск возникновения заболевания за счет большой численности группы может обеспечить высокий вклад больных этой группы в общую заболеваемость населения. И наоборот, высокий риск возникновения болезни в группе населения небольшой численности может проявиться незначительной долей заболевших.
Табл. 3. Заболеваемость дизентерией различных групп населения г. В. в 2000 г.
Как следует из данных табл. 3 – основной вклад (43.4%) в заболеваемость дизентерией в 2000 г. в г. В. внесли взрослые. Удельный вес детей, не посещающих ДДУ заболевших дизентерией, был в 4,5 раза меньшим и составил 9,6%. Однако, на основании только этих данных нельзя сделать вывод о том, что рискзаболеть дизентерией взрослых – наибольший, а аналогичный риск детей, не посещающих ДДУ – наименьший.
Различная доля заболевших в разных группах населения может быть связана не столько с разным риском заболеть дизентерией, сколько с различной численностью сравниваемых групп.
Именно поэтому соотношение интенсивных показателей оказалось прямо противоположным – риск заболеть дизентерией детей, не посещающих ДДУ был в 12 раз выше, чем аналогичный риск взрослых. Однако, сравнительно небольшой риск взрослых, за счет значительно большей их численности обеспечил почти половину всех больных дизентерией.
Таким образом, по величине экстенсивных показателей заболеваемости не следует делать выводы о частоте и риске заболеваемости в разных группах населения.
Исключением из этого правила являются такие распределения экстенсивных показателей, в которых оцениваются доли заболевших, относящихся к одной и той же группе населения
Поскольку все величины таблицы 4 относятся к одной и той же численности населения, т.е. численности населения Москвы в 2002 г., соотношение экстенсивных показателей соответствует соотношению интенсивных величин заболеваемости. Следовательно, таким же является и соотношение риска заболеть различными болезнями населения Москвы в 2002 г. Так, на основании представленных данных можно утверждать, что риск возникновения педикулеза был почти в 13 раз выше, чем риск заболеть скарлатиной (23,0/1,8=12,8).
Другая типичная ошибка связана с трактовкойдинамики экстенсивных показателей (табл. 5). Например, уменьшение удельного веса заболевших какой-либо группы пытаются объяснить влиянием факторов, определяющих заболеваемость только в той же группе, в частности, эффективностью противоэпидемических мероприятий, проводимых в отношении этой группы населения.
При изучении динамики экстенсивных показателей следует учитывать то, что уменьшение (увеличение) числа больных даже в одной группе и, следовательно, изменение общего числа больных, приведет к перераспределению долей во всех группах. Таким образом, наблюдаемое уменьшение (увеличение) вклада какой-либо группы в общую заболеваемость может быть связано с изменением численности больных как в этой, так и других группах населения.
Табл. 5.Заболеваемость болезнью К различных возрастных групп населения г. Н в течение 5 условных лет (Р – доля заболевших каждой группы в общей сумме заболевших за год).
Как следует из представленных данных, во всех группах, за исключением взрослых, отмечается явная тенденция снижения экстенсивных показателей заболеваемости. Однако было бы грубой ошибкой только на основании этого факта делать вывод о снижении риска заболеть болезнью К большинства групп населения г. Н.
Выявленная динамика экстенсивных показателей может быть следствием различных ситуаций, часть которых иллюстрируется табл. 6.
Табл. 6. Данные табл. 5 дополнены абсолютными числами заболевших (А).
Как следует из представленных данных, число заболевших в группах детей абсолютно не изменилось, тогда, как среди взрослых число заболевших постепенно увеличивалось. Учитывая, что численность возрастных групп не изменялась(см. примечание), без расчета интенсивных показателей можно сделать вывод о том, что риск заболеть болезнью К постепенно увеличился только для взрослого населения г.Н. В результате каждый год увеличивалось число заболевших среди взрослых и, естественно на ту же величину возрастало общее число заболевших среди всего населения. По этой причине, несмотря на то, что абсолютное число больных в остальных группах не изменялась, удельного веса заболевших детей постоянно снижался. Таким образом такое снижение произошло не за счет уменьшения риска заболеть в этих группах, а из-за увеличения риска заболеть взрослых и следовательно из-за увеличения общего число заболеваний. Поскольку общая численность всего населения не изменялась частота заболеваний болезнью К всего населения также увеличилась.
Заканчивая обсуждение интенсивных и экстенсивных показателей заболеваемости приведем сводную сравнительную характеристику свойств и возможностей этих показателей.
Расчет экстенсивных показателей
Экстенсивные коэффициенты характеризуют распределение явления на его составные части, его внутреннюю структуру или отношение частей к целому (удельный вес) и выражаются, как правило, в процентах или дробях.
При вычислении экстенсивных коэффициентов мы имеем дело только с одной статистической совокупностью и ее составом. Большинство экстенсивных коэффициентов обычно выражается в процентах, значительно реже они вычисляются в промилле или в долях единицы.
Методика вычисления экстенсивных коэффициентов проста. Например, в 2015 г. число всех заболеваний детей в детском саду составило 205 случаев, в том числе 72 случая бронхита. Составляем пропорцию:
т.е. удельный вес больных число больных определенной нозологией
в общем количестве больных число всех больных
В качестве примеров экстенсивных коэффициентов, применяемых в практике работы санитарно-противоэпидемической службы и в санитарной статистике, можно назвать структуру заболеваемости населения; распределение госпитализированных больных по отдельным нозологическим формам; состав санитарно-гигиенических исследований по видам анализов; структуру эпидемиологических обследований, сделанных врачами СЭС, по видам инфекционных заболеваний.
Необходимо предостеречь от попыток на основании экстенсивных коэффициентов, которые отражают только структуру той или иной совокупности, судить о частоте изучаемого явления. Для этой цели всегда необходимо знать численность среды, в которой происходят явления, и вычислить интенсивные коэффициенты.
Необходимые условия для расчета коэффициентов, используемых в эпидемилогии
1. Не следует делать выводы об изменении частоты явлений, основанные на коэффициентах структуры. Правильное заключение позволяют сделать только интенсивные коэффициенты.
2. Не следует производить складывание или вычитание статистических коэффициентов, вычисленных из совокупностей неодинаковой численности, так как это может привести к грубым ошибкам.
3. Следует правильно выбирать основание для коэффициента (например, коэффициент смертности женщин следует вычислять по отношению к числу женского, а не к числу всего населения; коэффициент летальности при гриппозной пневмонии вычисляется по отношению к больным, имевшим это осложнение, а не ко всем случаям гриппа вообще и т.д.)
4. Следует учитывать фактор времени и не сравнивать коэффициенты, вычисленные за различные периоды времени, что также может привести к ошибочным заключениям.
30. Аналитические методы исследования
Исследования типа кейс(случай)-контроль ( см. слайды 1-5 )и когортные исследования (см. слайды 6-10)
Оценка гипотез о факторах риска; определение направлений профилактики в соответствии с факторами риска.