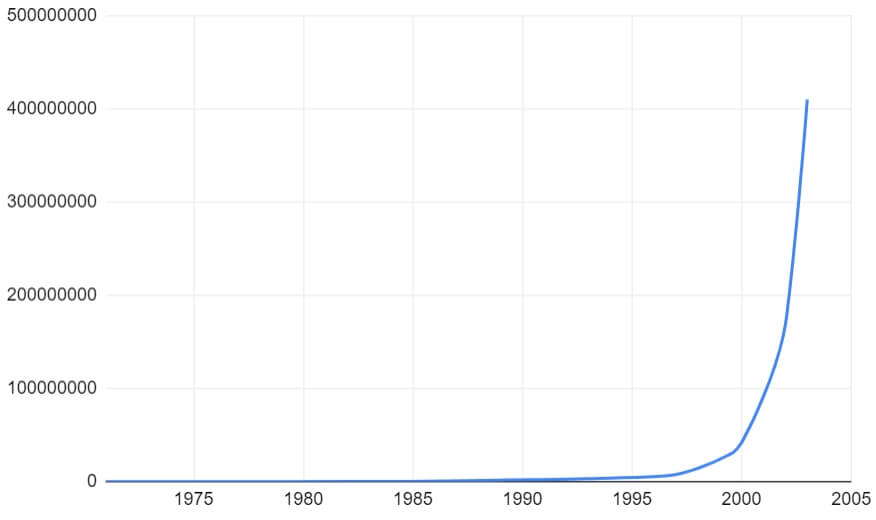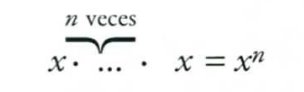Что означает экспоненциальный рост
Обманчивый мир технологий. Или экспоненциальный рост для «чайников»
Сегодня мы поговорим об экспоненциальном росте…
Стойте, не уходите! Я понимаю, звучит так, будто это не очень интересно и не совсем то, чего ожидаешь от сайта о мобильных технологиях. Но я вас уверяю, вы заблуждаетесь! Речь пойдет именно о том, о чем вам, как любителю современных технологий, точно хотелось бы знать.
Дело в том, что мы не совсем корректно понимаем многие процессы по той причине, что не можем осознать экспоненциальный рост (проще говоря, геометрическую прогрессию). Нет, логикой-то мы всё хорошо понимаем, но вот с осознанием как-то не складывается (вспомните легенду о зернах на шахматной доске).
Из-за этого получается такой парадокс — мы удивляемся, как быстро человечество перешло от калькуляторов к дополненной реальности (AR) и в то же время не видим дальше собственного носа, когда речь заходит о будущем.
После прочтения этой статьи, вы совершенно по-другому посмотрите на свой смартфон и на то, чем он может стать в скором времени!
Иллюзия прогресса, или что такое экспоненциальный рост
Если говорить простым языком, то экспоненциальный рост — это когда скорость роста какой-то величины зависит от ее размера. То есть, чем больше становится какое-то значение, тем быстрее оно растет. Снежный ком — неплохой пример экспоненциального роста.
Вроде бы все понятно, о чем тут еще говорить? Ну что ж, давайте проверим, так ли это.
Иллюзия обмана
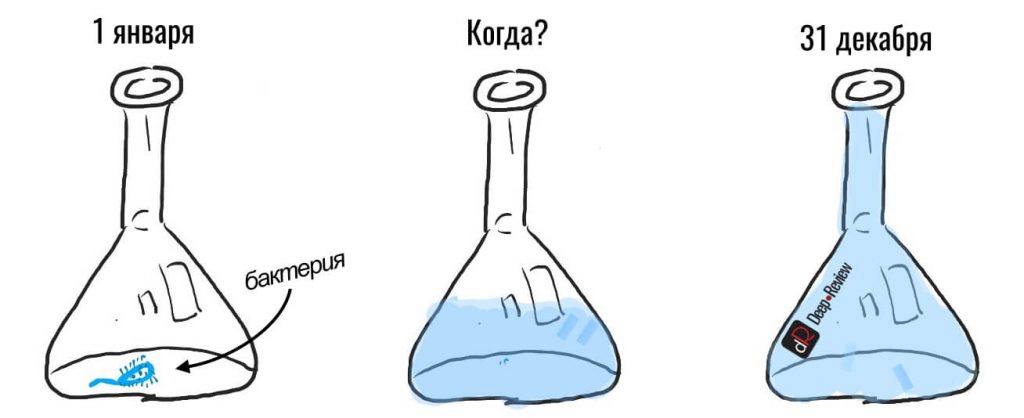
Вот у вас есть колбочка, в которую вы поместили одну бактерию. Число бактерий в колонии всегда растет экспоненциально. То есть, каждая бактерия делится на две, затем уже эти две делятся еще на две и получается четыре бактерии и так далее. Чем больше бактерий, тем быстрее будет расти их количество.
Предположим, что одна бактерия будет делиться на две ровно за один день. А вся колба заполнится бактериями за год, то есть, 31 декабря в колбе не останется больше места.
Внимание, вопрос! Если 1 января в колбе была 1 бактерия, а 31 декабря она заполнилась доверху, в какой день колба была заполнена ровно наполовину?
Наше «линейное» мышление всячески противится верному ответу: колба была заполнена на половину 30 декабря, ровно за 1 день до того, как места в ней больше не осталось.
И правда, если каждая бактерия 30 декабря разделится на две (то есть, произойдет то, что и происходило каждый день), то количество бактерий удвоится и, соответственно, полупустая колба заполнится.
Что же это получается? За целый год (без одного дня) мы с трудом собрали пол колбы бактерий, а на заполнение второй половины ушел всего день? Кажется, произошел взрывной рост!?
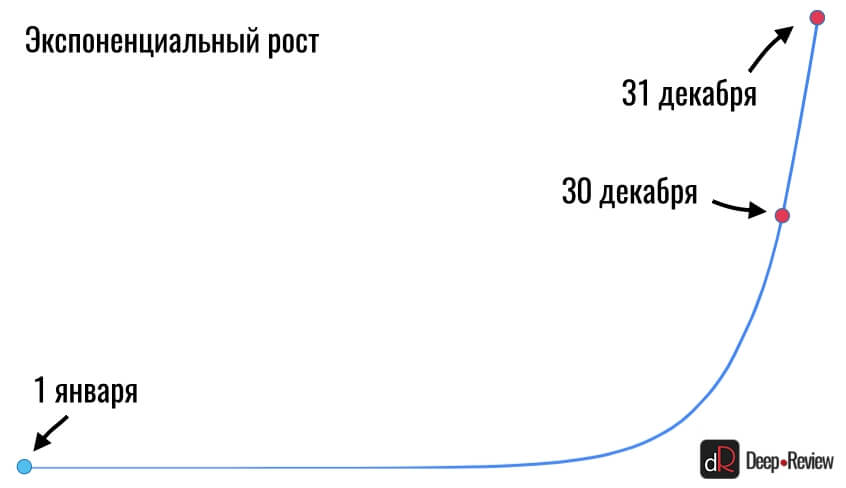
Вот как бы это все примерно выглядело на графике:
Ну вот мы и попались в ловушку! Ведь никакого взрывного роста под конец года не было. Темпы роста сохранялись на одном уровне в течение всего года — каждые день количество бактерий удваивалось.
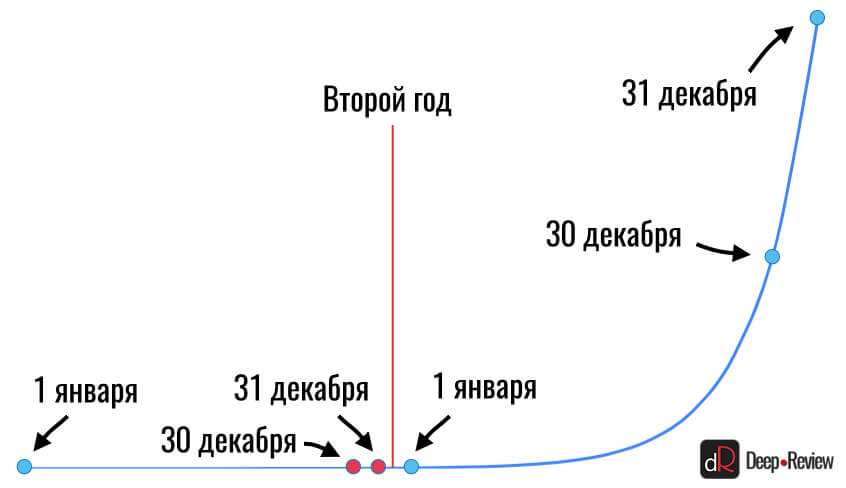
И теперь самое интересное! Если бы рост бактерий продолжился еще в течение следующего года, как вы думаете, где бы оказались наши точки 30 и 31 декабря? А вот где (показано красным цветом):
Как вам такое? Что же это теперь получается, на самом деле никакого взрывного роста в конце первого года не было? Ведь на графике эти точки находятся на прямой линии, а реальный рост начался ближе к концу второго года…
Я думаю, не нужно объяснять, что будет, если мы дальше продолжим наблюдать рост. Верно, кривая останется прежней, а наши «взрывные темпы роста» будут смещаться влево и превращаться в прямую линию. И каждый раз мы будем видеть одно и то же — ничего не росло в течение всего времени, а под конец — взрывной рост, пик, апогей!
«Как же нам повезло жить на пике технологий!»
Наверное, каждого посещали такие мысли. Ну правда, посмотрите, как человечество топталось на месте последние 40-50 лет и что произошло затем:
Согласен, график немножко спекулятивный, так как он показывает рост количества транзисторов в микропроцессорах, а это не совсем то же, что и рост производительности. Тем не менее, связь есть и мы ее прекрасно наблюдаем. Даже по своим смартфонам, сердцем которых и являются эти микропроцессоры.
А еще вы заметили, что красный график в точности повторяет экспоненциальную кривую, которую мы рассматривали на примере бактерий. То есть, можно смело утверждать, что последние 50 лет транзисторы уменьшались в размерах по экспоненциальной кривой. А из этого уже можно делать определенные выводы.
Когда современный молодой человек посмотрит на этот график, он ужаснется тому, как медленно развивались технологии с 1995 по 2005 гг., и подумает — как же здорово, что я живу сейчас, а не в «застойных нулевых»! А поразмыслив еще немножко, добавит — о каком прорыве может идти речь, мы ведь уже достигли апогея? Впереди только медленная эволюция.
Но, как мы уже убедились чуть выше, в этом и заключается обманчивость экспоненциального роста. В реальности этот график должен говорить такому молодому человеку совсем другое. Его должно пугать то, что может случиться через очередные пару лет, так как вся мощность, достигнутая наукой за последние 100 лет, просто умножится на 2! И тот апогей, которым он восторгался, окажется лишь прямой линией на графике.
Ну и, конечно же, молодой человек из далеких «нулевых» думал точно так же, как и наш современник, глядя на тогдашний экспоненциальный график роста количества транзисторов на микросхеме:
Не буду тратить ваше время, но поверьте мне на слово, таким этот график был в любой период времени и каждый раз простые обыватели думали, что вот он — пик развития, а впереди лишь медленная эволюция.
Поэтому, когда я в своей заметке «Восстание машин» говорил о том, что в ближайшие 10-15 лет наш мир может измениться до неузнаваемости, я просто руководствовался здравым смыслом, зная о существовании логической ловушки под названием экспоненциальный рост.
Процессоры — не бактерии!
Но с чего, вдруг, я взял, что транзисторы должны уменьшаться по экспоненциальному росту? Это что, какой-то неизвестный миру «4-й закон Ньютона»?
Хорошее замечание! И на самом деле не существует никакого закона, которому бы могло подчиняться изменение размеров транзисторов. Мы не можем со стопроцентной уверенностью заявлять, что экспоненциальное развитие технологий продолжится. Но у нас есть десятки лет истории, из которой можно сделать 3 простых вывода:
А если это звучит неубедительно и вы понимаете английский, тогда рекомендую посмотреть интереснейшее интервью с Джимом Келлером — гениальным инженером и вице-президентом компании Intel. Похоже, нас ждут очередные 20 лет экспоненциального развития технологий.
Это значит, что современный взрывной рост (мощные смартфоны, голосовые ассистенты, дополненная реальность и вычислительная фотография) через 10 лет окажется всего лишь прямой линией на графике.
Кстати, не только количество транзисторов растет экспоненциально. В мире есть и множество других примеров. Население земли — один из них. Вдумайтесь только, тысячи лет истории привели к появлению первого миллиарда человек на планете. На второй миллиард ушло всего 100 лет. К отметке в 3 миллиарда мы подошли за 30 лет. А в последнее время население земли увеличивается на 1 миллиард каждые 10 лет.
Алексей, главный редактор Deep-Review
P.S. Не забудьте подписаться в Telegram на первый научно-популярный сайт о мобильных технологиях — Deep-Review, чтобы не пропустить очень интересные материалы, которые мы сейчас готовим!
Как бы вы оценили эту статью?
Нажмите на звездочку для оценки
Внизу страницы есть комментарии.
Напишите свое мнение там, чтобы его увидели все читатели!
Если Вы хотите только поставить оценку, укажите, что именно не так?
Экспоненциальный рост
Журналисты, блогеры и диванные эксперты… Все используют фразы «экспоненциальный рост», а кто по проще «рост по экспоненте». Кое-кто, наверное, даже помнит, что такое экспонента, но вряд ли сможет объяснить простыми словами. Что же, пришла пора разобраться то, чем мы так часто пользуемся. Возможно, все совсем не так…
Экспонента
Здесь все просто (но это только пока). Многие считают, что экспонента это просто число е=2,718281828459045235360287. Конечно, это не так. Это самое число e, называется числом Эйлера, оно трансцендентно и иррационально, что звучит красиво и загадочно, но экспонента, не число, а функция.
Те, кто немного дружил с математикой в школе сразу заметят интересную особенность этой функции. Ее основанием является не отрицательное число, а значит, она будет всегда возрастать.

При х=0 у=1, при х=1, у=2,718, при х=2 y=7,39…. Ну а при х=10, у=22 026,5
Значение функции растет и растет явно очень быстро. Стремительно и неудержимо.
Экспоненциальный рост
Что такое экспоненциальный рост? Простыми словами, это такой рост, при котором, чем больше вырастят какое-либо значение, тем больше ускоряется его рост. То есть, со временем растет не только значение, но и сама скорость его роста.
А это, иными словами, означает, что значение переменной функции и скорость ее роста находятся в прямо пропорциональной зависимости. То есть, если значение увеличиться два раза, скорость роста увеличится тоже в 2 раза.
В конечном итоге, экспоненциальный рост — самый быстрый.
На самом деле, все вышесказанное касается любой показательной функции, а не только экспоненты.
Основанием может быть любое не отрицательное число, хоть два, хоть три, хоть… сколько угодно.
Несколько примеров из жизни
Самым актуальным и наглядным можно назвать ситуацию с распространением вируса (либо любой другой инфекции). Предположим, что каждый человек в течение дня заражает двух других. Тогда, в первый день у нас будет один инфицированный, во второй — трое. Один старый знакомый и два новых. Каждый из новичков, в свою очередь заразит двух других. В третий день — 7 заразившихся, в четвертый — 1, а пятый — 31… Стоп, это только при условии, что каждый человек заразит только двоих и, чудесным образом, перестанет это делать на притяжении следующих дней. Но ведь так не будет! Все эти люди и дальше будут заражать по 2 человека в день.
А раз так, то на третий день будет уже 9 разносчиков вируса, на пятый — 81, а через неделю по нашему воображаемому городу будет бродить уже 729 зараженных.
Это и будет экспоненциальный рост количества зараженных. Без учета их лечения, карантина или любых других мер, болезнь будет развиваться именно так. Через 10 дней зараженных людей будет уже 59 тысяч человек. Через 15 дней — более 14 миллионов. Просто математика, но какой яркий пример экспоненциального роста?
Легко вывести формулу: 1, 3, 9, 27, 81… это «три» в степени 2, 3 и 4. То есть, показательна функция с основанием 3.
И, хотя в этой формуле в степень возводится не число Эйлера (2,71828….), такой рост тоже называется экспоненциальным.
Еще один пример из биологии: размножение бактерий.
Бактерии размножаются делением. Каждая делится надвое и так далее… Но, конечно, не бесконечно. Предел есть, но об этом чуть позже.
Экспоненциальный рост в экономике
Есть примеры роста по экспоненте и в экономике. Самый интересный — финансовая пирамида. Самый безопасный — Закон Мура.
Первый закон Мура гласит, что количество транзисторов удваивается каждые 2 года. Таким образом и вычислительные мощности компьютера удваиваются каждые два года.
Второй Закон Мура (который сформулировал уже не Гордон Мур) гласит, что стоимость производства микросхем также возрастает экспоненциально из-за усложнения технологий.
Что же касается финансовых пирамид, то основная идея в том, что их рост обусловлен исключительно ростом количества «сектантов» верящих в огромные прибыли или тех, кто верит, что сумеет вовремя «соскочить». Так или иначе, пирамиды всегда рушатся. И вот вопрос, почему?
Но, конечно, рост не может продолжаться бесконечно. В случае с бактериями (и любыми другими организмами, да хоть мышами), наступит время, когда им не хватит пространства и пищи. В случае с микросхемами наступит физический предел скорости передачи данных (мы вряд ли сумеем превысить скорость света). Ну а всевозможные волшебные экономические модели в форме пирамид рано или поздно сталкиваются с той же проблемой, питательная среда в виде легковерных последователей
Логистическая кривая
В реальном мире, не таком идеальном как математика, любой процесс может столкнутся с пределом. В примере роста популяции бактерий или даже крупных животных, это количество ресурсов, которое всегда ограничено. Поэтому, при условии, что ресурсы не бесконечны, процесс развивается по s образной кривой. Сначала стремительно растет, а потом — замедляется.
В пример с вирусом, наступает день, когда большая часть населения уже переболела и выработала антитела (либо была искусственно привита) и вирус больше не может распространяться по экспоненциальному закону. Главный вопрос, можно ли точно предсказать этот день?
Мальтузианская ловушка
С экспонентой связан еще один занимательный экономический эффект — «мальтузианская ловушка». Представьте, что рост населения страны происходит по экспоненциальному закону. Например, каждая пара производит на свет не менее 4 детей, те в свою очередь поступают также. Рано или поздно, количество людей превысит количество пищи, необходимое для нормальной жизни.
Просто потому, что производительность труда физически ограничена (например, количеством плодородных земель), к тому же развитие технологий чаще всего происходит линейно, а экспонента всегда растет быстрее. Получается, что технологическое развитие общества не успевает за ростом населения.
Чем это заканчивается? Кризисом, голодом, войнами за ресурсы. Население уменьшается и все начинается с начала.
Почему это сложно представить?
Нам, людям, сложно себе представить развитие процесса «по экспоненте» потому, что не свойственно так мыслить. Мы привыкли к линейным и циклическим процессам. Они чаще встречаются в нашей жизни: циклические изменения дня и ночи и линейные изменения времени. Это просто и привычно. А вот экспоненциальные процессы встречаются реже.
Тем не менее они есть и игнорировать их опасно. Просто потому, что за этой скоростью нашему разуму сложно угнаться. Даже простые объяснения экспоненциального роста кажутся чем-то абстрактным, а ведь это не выдумка, а наша реальность.
Экспонента в математике – это функция «y=ex», которая отражает непрерывный рост с коэффициентом. В этой функции «е» – это число Эйлера, которое представляет собой постоянную (
2,72). Говоря иначе, рост любой величины прямо пропорционален ее значению.
Допустим, мы слепили снежный ком и спустили его с горы. Он начинает катиться, одновременно наращивая объем. При этом чем больше он становится, тем выше скорость его движения. И наоборот: чем быстрее он катится, тем быстрее увеличивается в размерах. Получается, что масса и скорость снежного кома (y) экспоненциально возрастают со временем (x).
Экспонента в жизни. Экспоненциальный рост
Рассмотрим примеры экспоненты и экспоненциального роста в реальной жизни.
Вклад в банке под процент. У всех процессов, идущих по экспоненте, есть одна особенность: за одно и то же количество времени их параметры меняются одинаковое количество раз.
Например, вклад в банке каждый год увеличивается на определенное количество процентов. Если положить 1000 рублей в банк под 10% годовых, то через год вклад будет составлять 1100 рублей. А в следующем году 10% будут начисляться уже исходя из суммы в 1100 рублей. То есть, вклад вырастет сильнее, и так размер прироста будет увеличиваться из года в год.
Численность животных. Чем больше популяция животных, тем больше они размножаются. Соответственно, рост численности популяции прямо пропорционален количеству особей в ней.
Чем экспоненциальный рост отличается от линейного?
Линейный рост характеризуется стабильным прибавлением постоянной, а экспоненциальный рост – это следствие многократного умножения на постоянную. То есть если линейный рост на графике представляет собой стабильную линию, то экспоненциальный рост характеризуется быстрым взлетом.
В качестве примера можно привести обычную ходьбу. Если длина одного шага составляет 1 метр, то через 6 шагов человек преодолевает расстояние в 6 метров. Это и называется линейным ростом.
При экспоненциальном росте длина каждого шага в нашем примере увеличивается в 2 раза. То есть сначала человек шагает на 1 метр, потом на 2 метра, потом на 4 метра и так далее. В таком случае за 6 шагов можно пройти 32 метра, что гораздо больше, чем в предыдущем примере.
Математическая вселенная: экспоненциалы и экспоненциальный рост простым языком
Геометрическая прогрессия — опасная вещь. Стоит выпустить экспоненциальный рост из-под контроля, и случится непоправимое: Землю заполонят мириады бактерий и крыс, размножающихся чудовищными темпами, все компьютеры станут бесполезны, так как время обработки данных будет уходить в плюс-бесконечность… В экспоненциальном спаде тоже нет ничего приятного: вспомним хотя бы ядерные катастрофы. Тем не менее, экспоненциалы постоянно присутствуют в нашей жизни, и благодаря их использованию перед человечеством открываются интереснейшие возможности.
В науке словосочетание «экспоненциальный рост» — словно упоминание дьявола. Оно может означать лишь одно — неконтролируемое возрастание величины в геометрической прогрессии.
Экспоненциальный рост приводит к катастрофам — что в биологии, что в информатике.
Экспоненциалы. Алгебра роста
На фото мы видим бесконечность в отражениях зеркал. Данный пример наглядно иллюстрирует принцип экспоненциальной алгебры. Отражения становятся все меньше и образуют убывающую последовательность. Это и называется геометрической прогрессией.
Давайте представим, что у нас есть бактерия, растущая в чашке Петри. Она помещена н благоприятную среду, где может питаться и воспроизводиться. Через 20 минут от нее отделяется вторая бактерия. И через каждые 10 минут — следующая. То есть через 40 минут вместо одной первой бактерии у нас будут уже четыре микроорганизма, а через час — восемь. Каждый из них весит очень мало — около одной биллионной грамма (0,000000000001 г), то есть для того, чтобы общий вес бактерий достиг одного грамма, их нужен один биллион. Итак, вопрос следующий: каков будет вес посева через 48 часов? Мы помним. что данный вид бактерии воспроизводится каждые 20 минут. Смело заключайте пари — вы выиграете. Даже хорошо умеющие считать люди здесь, скорее всего, допустят ошибку. Итоговый вес бактерий будет в четыре тысячи раз превышать вес Земли. Конечно, в маленькой чашке Петри этого не получится, потому что в определенный момент бактерии из-за количества выделяемых ими отходов жизнедеятельности просто перестают размножаться. Но если представить себе, что этого не происходит, то станет понятно, насколько быстро «плохие» бактерии смогут решить вопрос с перенаселенностью планеты.
Бактерии, растущие в чашке Петри. Деление через равные промежутки времени является экспоненциальным ростом, и останавливают его лишь ограниченные стенками чашки пищевые ресурсы; в природе воспроизводство этих бактерий может быть разрушительным.
Результаты подобных вычислений, всегда поражающие своими немыслимыми пропорциями. в математике называются экспоненциальным ростом. Расчеты прироста популяции относятся именно к этой части математики, и числа, которыми они оперируют, не перестают удивлять. Например, если одна пара крыс четыре раза в год будет производить по четыре крысенка, то всего лишь через 60 поколений крысы полностью покроют поверхность Земли.
Пара определений
Операция, где число x складывается само с собой столько раз, сколько требует число n, называется умножением.
В свою очередь умножение числа х на само себя n-ное количество раз называется возведением в степень.
Число x — это основа, а число n — показатель степени (экспонент).
Считается, что последовательность чисел растет линейно с увеличением константы скорости, то есть каждое следующее значение может быть получено путем добавления определенного числа к предыдущему. Например:
где таким числом является три. Это фиксированное значение, которое прибавляется к каждому числу для получения следующего. Если n — позиция, занимаемая предыдущим числом, то се значение можно изобразить так: ƒ(n), где ƒ(n)=n+3.
Если же значение величины возрастает не в результате сложения, а благодаря умножению каждого числа на определенный множитель, то здесь мы имеем дело с экспоненциальном ростом (возрастанием в геометрической прогрессии), как в следующем случае:
Правила возведения в степень
Масштаб
Масштаб выражается на языке математических символов как десятичная степень основного размера — метра. Слева направо: галактика, насчитывающая, предположительно, 10 11 звезд и находящаяся на расстоянии 10 15 м от нашей планеты; земной шар, диаметр которого около 10 7 м; элемент рельефа литосферы порядка 10 3 м.
Ритм шахмат
Существует легенда, ярко иллюстрирующая коварство экспоненциального роста. В ней говорится о человеке, придумавшем шахматы. В награду за его изобретение султан предложил ему выбрать любое сокровище. И тот попросил зерна.
Он захотел, чтобы ему дали столько зерна, сколько клеток на шахматной доске, причем с условием, что на первую клетку будет положено одно зерно, а на каждую последующую — в два раза больше, чем на предыдущую. Правитель, неважнецки разбиравшийся в математике, с легкостью согласился. Он даже не представлял, что зерна, выращиваемого на всей Земле, окажется недостаточно. Несмотря на то, что многие знакомы с этой историей или хотя бы слышали о ней, подловить кого-нибудь тем же способом труда не составит. Можно просто предложить положить одну копейку на первую клетку доски, две — на вторую, четыре — на третью и т. д. Не стоит заключать подобный договор в присутствии нотариуса, ведь никому не по силам ни заплатить конечную сумму, ни даже приблизиться к ней: речь идет о богатстве, накопленном человечеством за все долгие века своего существования. Сумма, о которой мы сейчас говорим, равна 18 446 744 073 709 551 615 рублям.
Типы процентов
Пример экспоненциального роста из повседневной жизни — сложный процент. Сравнение простых и сложных процентов позволяет ясно увидеть разницу между линейной и геометрической прогрессиями. Допустим, вы решили положить в банк 1000 рублей под процентную ставку 5% годовых. За первый год ваш вклад возрастет до 1000+50=1050 рублей, за второй — до 1050+50=1100, за третий — до 1100+50=1150.
Здесь речь идет о линейном росте, где каждое следующее значение получено путем прибавления 50 к предыдущему. Капитал ƒ(n) через n лет:
И наоборот, если речь идет о вложении на 10 лет по сложной процентной ставке 5% годовых, то, используя формулу
где C0 — исходный капитал, i — ставка, а n — количество лет, мы получим следующее:
1000; 1000*(1+0,05); 1000*(1+0,05) 2 ; 1000*(1+0,05) 3 ; 1000(1+0,05) 4 …
после определенных операций, станет таким:
1000; 1050; 1102,5; 1157,6; 1215,5…
Как можно заметить, каждое следующее значение получено из предыдущего путем умножения на коэффициент 1,05. Выше находится сравнительная таблица двух видов ставок; отбросив знаки после запятой, мы увидим, что разница между двумя числами очень мала на протяжении первых двух лет, но затем, по прошествии времени, она заметно увеличивается. Если представить эти значения в виде двух линий на графике, по вертикальной оси которого будут откладываться годы, а по горизонтальной — капитал, то у нас получится диаграмма как на картинке ниже. Соединив точки, мы увидим, что кривая, соответствующая сложным процентным ставкам (красного цвета), растет быстрее, чем та, что соответствует простым (зеленого цвета).
Графики роста вкладов с простыми и сложными процентными ставками (зеленый и красный цвета соответственно) для начального вложения в размере 1000 рублей под 5% годовых.
Если бы речь шла о вкладе на 24 года (на таблице не отображен такой срок), то к концу этого периода вклад по сложной процентной ставке вырос бы до 3225, тогда как по простой ставке он достиг бы всего лишь цифры 2200. Разница достаточно заметна.
Наглядное представление
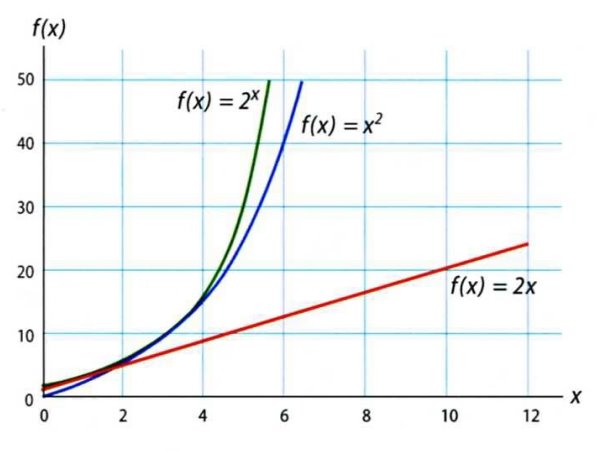
График наверху наглядно иллюстрирует пример со вкладами, однако с математической точки зрения он неточен — экспонент всегда выражается кривой, и эта кривая «поднимается» настолько быстро, что, как правило, приходится задавать разный масштаб горизонтальной и вертикальной осям, иначе линия просто выйдет за пределы рисунка. На изображениях ниже представлен линейный рост типа 2, 4, 6, 8… красным цветом и экспоненциальный рост 2, 4, 8, 16… – зеленым.
Сравнительный график линейного (красный), полиномного (синий) и экспоненциального (зеленый) роста.
Как видно из графика, начиная с номера 2 по шкале x кривая резко уходит вверх, удаляясь от прямой. Первая из них — это функция вида ƒ(x)=2x, где мы получаем последовательность, в которой x равен 1, 2, 3… В отличие от первой функции, вторая выглядит так: ƒ(x)=2 x . Для получения ряда необходимо поднять до 2 экспоненты 1, 2, 3…
На таблице выше видно, что вновь появившееся значение достигает х 2 на уровне номера 4, где обе кривых получают одинаковое значение — 16, но с этого момента экспонент начинает все больше отдаляться. Вопрос теперь состоит в том, что произойдет, если вместо возведения в квадрат (ƒ(х)=х 2 ) числа 2 мы увеличим показатель степени и возьмем, например, 5(ƒ(х)-х 5 ). Рисунок с изображением данного ряда получился бы чересчур громоздким. Но можно заметить, что номер 8 имеет значение 8 5 =32768, и оно гораздо выше значения 64, которое соответствовало бы экспоненциальному ряду. Значит ли это, что ряд
растет быстрее, чем
До определенного предела. Точнее сказать трудно, ведь начиная с известного момента экспоненциальный ряд получает значительное преимущество. Например, для номера 50 это 50 5 =312500000, при том что 2 50 =1125899906842624. То есть можно с абсолютной уверенностью утверждать, что на номере 50 экспоненциал не только перегнал соответствующую точку конкурентного ряда, но и удаляется от нее на огромной скорости.
Этот факт имеет огромное значение для некоторых областей программирования. При попытке разрешить определенную проблему путем установки на компьютер специальной программы жизненно необходимо, чтобы количество совершаемых шагов увеличивалось полиномным образом, сообразно сложности задачи, то есть в соответствии с ростом числа данных, поступающих в программу. Когда это не так, и время работы программы по мере ввода новых данных растет в геометрической прогрессии, то время выполнения, в течение которого машина должна представить результат, затягивается настолько, что ее использование становится нецелесообразным. Большая часть программного обеспечения, применяемого для шифрования данных — персональных, банковских или военных — основывает свою безопасность именно на этом. Существуют программы для вскрытия цифровых кодов, но на подбор ключей им требуется целая пропасть времени. На взлом могут уйти сотни миллионов лет.
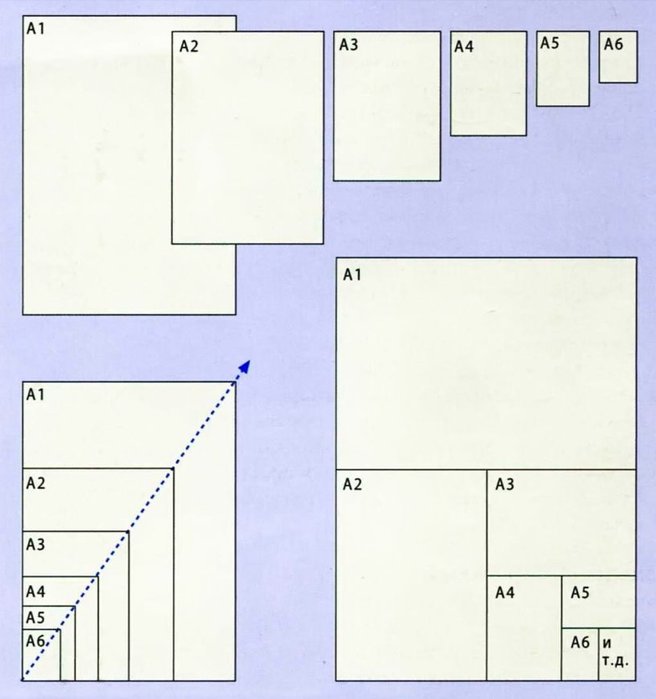
Стандарты DIN
Видение Мальтуса
Пересечения линий и кривых на графиках линейного и экспоненциального роста позволяют увидеть определенные закономерности и предсказать будущее. Томас Роберт Мальтус (1766–1834) — британский экономист, ученик Адама Смита — в своей работе «Опыт о законе народонаселения» выдвинул тезис, что рост населения скоро превысит возможности Земли производить пропитание.
Портрет Томаса Роберта Мальтуса, одного из родоначальников политэкономии и основателей демографии.
Мальитус подчеркивал: «Достаточно владеть элементарными навыками счета, чтобы оценить огромную разницу между двумя силами и склониться к первой». Здесь он сравнивал линейное и экспоненциальное поведение двух тенденций.
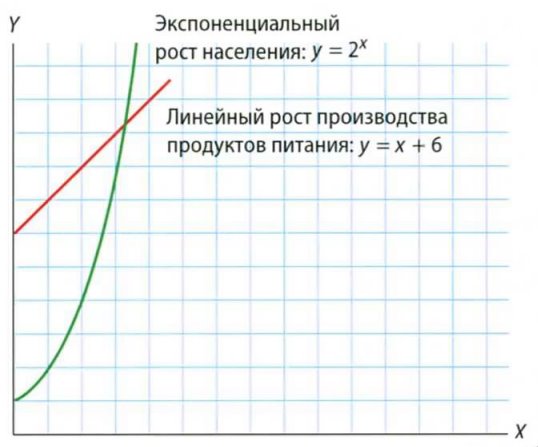
Теория Мальтуса: производство продуктов увеличивается линейно, а население — экспоненциально.
На графике можно видеть, что пока мы не достигнем точки, где линии пересекаются, производство продуктов питания будет больше, чем рост населения земли. Но затем кривая населения начинает стремительно удаляться от прямой, отражающей производство средств существования.
По мнению Мальтуса, «если предположить, что население земли равно миллиарду человек, человеческий род будет расти как числа: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512 и т.д., в то время как средства существования будут прибавляться следующим образом: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 и т.д. Через два века с четвертью соотношение населения и средств существования будет 512 к 10; еще через три века эта пропорция станет 4096 к 13, а еще через две тысячи лет разницу окажется невозможно подсчитать, несмотря на немыслимые размеры производства». Мы не будем вдаваться в анализ теории Мальтуса, но отметим, к каким интересным выводам ему удалось прийти путем простого сравнения арифметической и геометрической прогрессий.
Книга «Опыт о законе народонаселения» была анонимно выпущена в 1798 году и обрела огромную известность во всех уголках земного шара. На картинке — французское издание 1809 года.
Экспоненциальный спад
Экспоненциальное поведение включает в себя не только рост, но и обратный процесс, называемый экспоненциальным спадом. Механизм такого уменьшения очень похож на предыдущий, но лишь с той разницей, что оно пропорционально каждой из присутствующих величин. Например, первоначально заданное число 100 при скорости спада 0,5 даст нам серию чисел:
100; 50; 25; 12,5; 6,25 и т.д.,
где каждое следующее число получается благодаря умножению предыдущего на 0,5 (что равносильно его делению на 2). В общем, при экспоненциальном спаде каждое число получается путем умножения предыдущего на постоянную величину, которая должна быть меньше единицы.
Характерный пример этого вида уменьшения — радиоактивный распад. Ядра радиоактивного вещества распадаются естественным путем. Время tполураспада определяется как время, необходимое для того, чтобы количество n ядер уменьшилось в два раза. Так как количество происходящих распадов пропорционально количеству радиоактивных ядер, то процесс дезинтеграции представляет собой экспоненциальный спад. Представим себе, что если t — это период полураспада, то, пока он происходит, образец m уменьшается в два раза m/2, и через соответствующие периоды времени действие продолжается по той же схеме: m/4, m/8, m/16…
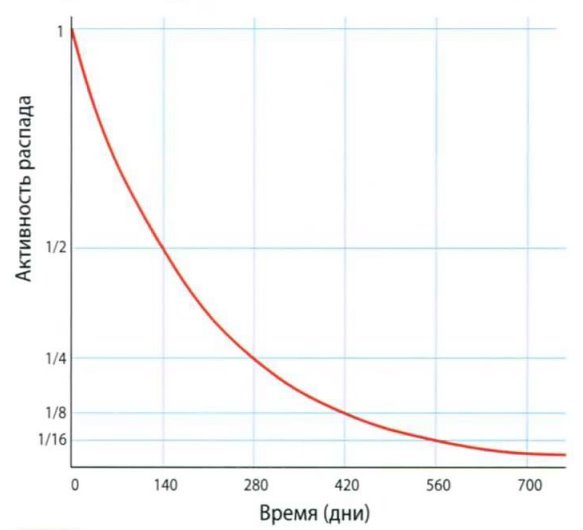
График экспоненциального замедления распада полония. Активность распада атомов снижается вдвое каждые 140 дней.
Например, период распада полония составляет 140 дней. На графике дни отмечены по горизонтальной оси, а общая выборка — по вертикальной. Проведя линию от точки, которая отмечает 140 дней, мы видим, что она соответствует уменьшению первоначального количества радиоактивных ядер в два раза. Характерная кривая экспоненциального распада та же, что и при экспоненциальном росте. Единственное их отличие в том, что одна «поднимается», а вторая «опускается». Это явление находит практическое применение в датировке археологических и геологических памятников.
Радиоуглеродный анализ позволяет устанавливать возраст археологических находок по периоду полураспада изотопа углерода.
Чаще всего для определения абсолютной хронологии используется 14 C — нестабильный изотоп углерода, содержащийся в атмосфере. На протяжении всей жизни животные и растения впитывают и усваивают его вместе со стабильными изотопами углерода, а после смерти организма 14 C начинает распадаться, и период полураспада составляет 5568 лет. Для определения возраста методом радиоуглеродного анализа в содержащих органику археологических находках подсчитывается количество 14 C и сравнивается с количеством стабильных изотопов.
Есть и другие экспоненциальные распады, не такие сложные, как этот. Вероятно, распад аромата фруктов или томатов — это процесс со схожими характеристиками. Другой пример был приведен популярным в Твиттере математиком Джоном Алленом Паулосом из Висконсинского университета — он высказал предположение, что количество читателей математического текста уменьшается в два раза после каждой формулы, встретившейся в нем. Быстрый подсчет позволил бы нам увидеть, что до этих последних строчек дошли лишь очень немногие из начинавших читать данную статью.
Это интересно!
В последние годы развитие персональных компьютеров состояло в постоянном увеличении их возможностей — скорости процессора, емкости жесткого диска и оперативной памяти.
Относительно последней любопытно отметить, что рост ее объема происходил по экспоненциальному типу:
1, 4, 8, 16, 32, 64, 128, 256, 512, 1024…
Еще на десерт. Написание
то есть одной единице с 10 миллиардами нулей. Это число огромно! Большие значения всегда легче записывать, используя степени, хотя обычно они и не соответствуют никакому реальному количеству. Одно из самых длинных чисел, когда-либо использовавшихся в математике, это число Фолкмана:
Его размер был почти что невообразим. Это значение встречается в теории графов и показывает минимальное количество вершин, которое должен иметь граф, удовлетворяющий определенным условиям. Это число было открыто в конце XX века.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.