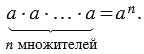Что означает число в кубе
Степень числа. Квадрат и куб числа
Определение.
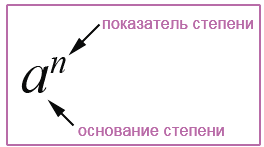
Степенью числа «
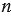
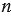

Например, найдем значение следующих степеней:
2 4 = 2





3 6 = 3














Например, найдем квадрат чисел 4 и 8:
4 2 = 4
8 2 = 8
Например, найдем куб чисел 5 и 7:
5 3 = 5


7 3 = 7


Степенью числа «
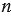
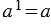
Сначала выполним возведение во 2 степень числа 4, затем находим значение выражения, находящегося в скобках, после чего выполняем умножение, и последним действием выполняем вычитание:
Поделись с друзьями в социальных сетях:
Таблица кубов
Таблица кубов или таблица возведения чисел в третью степень. Интерактивная таблица кубов и изображения таблицы в высоком качестве.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 1 | 1000 | 1331 | 1728 | 2197 | 2744 | 3375 | 4096 | 4913 | 5832 | 6859 |
| 2 | 8000 | 9261 | 10648 | 12167 | 13824 | 15625 | 17576 | 19683 | 21952 | 24389 |
| 3 | 27000 | 29791 | 32768 | 35937 | 39304 | 42875 | 46656 | 50653 | 54872 | 59319 |
| 4 | 64000 | 68921 | 74088 | 79507 | 85184 | 91125 | 97336 | 103823 | 110592 | 117649 |
| 5 | 125000 | 132651 | 140608 | 148877 | 157464 | 166375 | 175616 | 185193 | 195112 | 205379 |
| 6 | 216000 | 226981 | 238328 | 250047 | 262144 | 274625 | 287496 | 300763 | 314432 | 328509 |
| 7 | 343000 | 357911 | 373248 | 389017 | 405224 | 421875 | 438976 | 456533 | 474552 | 493039 |
| 8 | 512000 | 531441 | 551368 | 571787 | 592704 | 614125 | 636056 | 658503 | 681472 | 704969 |
| 9 | 729000 | 753571 | 778688 | 804357 | 830584 | 857375 | 884736 | 912673 | 941192 | 970299 |
Таблица кубов
Теория
Куб числа – это результат умножения числа само на себя три раза. Операция вычисления куба числа – это частный случай возведения числа в степень, в данном случае в втретью:
Данное выражение читается: «возвести в куб число 6» или «6 в кубе».
Скачать таблицу кубов
Таблица кубов и квадратов, как состовлять и найти
Как появилось понятие куб числа?
Древнегреческие математики оперировали так называемыми фигурными числами – числами, которые можно представить в виде фигуры. Выделялись, например:
Последовательность кубов натуральных чисел выглядит так
Полезно будет запомнить, хотя бы те, что меньше тысячи. Особенно мне нравится число 729. Посмотрите:
Еще несколько интересных свойств кубов чисел:
Вот так, к слову выглядит формула вычисления суммы первых кубов чисел:
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
Возвести число в куб — значит умножить его само на себя три раза.
Возвести число в натуральную степень — значит умножить его само на себя раз:
Теория
Куб числа – это результат умножения числа само на себя три раза. Операция вычисления куба числа – это частный случай возведения числа в степень, в данном случае в втретью:
Данное выражение читается: «возвести в куб число 6» или «6 в кубе».
Возвести в куб онлайн
Как возвести число в куб онлайн!? Введите нужное число, которое требуется возвести в куб и нажмите возвести в куб. Справа от равно появится число, которое возвели в куб
Ну и далее пробежимся по нескольким поисковым запросам, которые так или иначе вы задаете в строке поиска!
Дополнительная информация
Квадратом числа называют произведение двух одинаковых множителей.
Мы уже пробовали находить квадраты первого десятка натуральных чисел.
Возводить двузначные числа, трехзначные и т.д. числа немного сложнее, главное хорошо знать и помнить таблицу умножения чисел.
Существует способ быстрого возведения в квадрат двухзначных чисел, которые оканчиваются на цифру 5.
1) Первую цифру числа, возводимого в квадрат, необходимо умножить на сумму этого числа и единицы.
2) Записать полученное число- это будут первые цифры ответа (с этих цифр начинается ответ).
3) Ответ всегда будет заканчиваться на 25 (т.е. в конце ответа всегда будет стоять число 25).
4) Приписываем к числу, полученному в п 2, число 25, получаем ответ.
Рассмотрим поясняющий пример.
Найдем квадрат 65.
65 2 = 65 ∙ 65
6 ∙ (6 + 1) = 6 ∙ 7 = 42
Запишем число 42 и припишем к нему число 25.
65 2 = 4225
Проверим: Так как квадрат числа- это произведение двух одинаковых множителей 65 2 = 65 ∙ 65, то
65 2 = 65 ∙ 65 = 4225
Получили все тот же ответ: 65 2 = 4225