Что означает числитель и знаменатель в расписании
Что значит числитель и знаменатель в расписании?
Что обозначает числитель и знаменатель в расписании для студентов?
Можно узнать в расписании недель, какой является неделя в учебном семестре – по числителю или по знаменателю. Что это значит? Как в этом разобраться?
В высших учебных заведения достаточно много предметов. Кафедры общественных наук (философия, история, политология и пр.) читают лекции и проводят семинары у всех студентов, учащихся в этом учебном заведении, вне зависимости от специальности. Опять же количество часов по разным предметам неодинаковое и их равномерное распределение на весь семестр достаточно сложный, трудоемкий и гибкий процесс. Поэтому в ВУЗах применяют двухнедельное расписание. В числителе стоит расписание на 1-ю неделю (нечетную), в знаменателе на 2-ю (четную).
Отчет недель начинается с 1 дня начала семестра. Часто на расписании указывают по какой неделе проходят занятия. Т.е. каждый понедельник меняют цифры 1 и 2.
Числитель и знаменатель в расписании.
Для тех, кто еще не сталкивался с таким видом расписания. Предмет, урок или пара, при таком расписании может в одну неделю быть, а в другую нет. Или в одну неделю один предмет в это время, а в другую неделю в это же время другой предмет.
Выглядит это следующим образом:
строчка в расписании делится на две строки (одна строка под другой или строки через косую линию), в каждой из которой написан разный предмет.
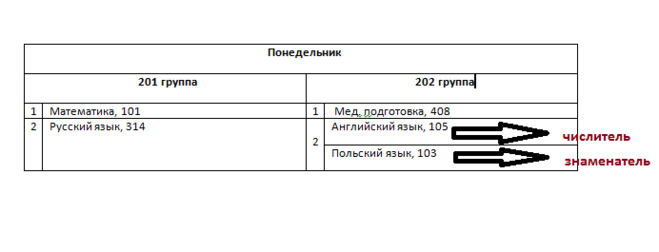
Вот простенький пример, как выглядит подобное расписание, и показано, где числитель, и где знаменатель:
Давайте разберем подробно, что значит «числитель» и «знаменатель» в расписании занятий для студентов в ВУЗах и других учебных заведениях.
Идем дальше. Расписание составляется на основе установленной образовательной программы. Каждый предмет имеет определенное количество часов для проведения семинаров и лекций. Возьмем два произвольных предмета: Предмет А и предмет Б. У предмета А количество академических часов солидно больше, чем у предмета Б. Поэтому методисты ставят пары по числителю и знаменателю, чтобы уместить все необходимые часы обучения. То есть идет предмет Б, но только по четной учебной неделе. На нечетной неделе он заменяется предметом А. В расписании это обычно выглядит как одна клетка для определенного дня, разделенная горизонтальной полосой. Сверху числитель(нечетная неделя), снизу знаменатель(четная неделя).
Вот наглядный пример числителя и знаменателя на примере расписания ВУЗа, в котором училась когда-то я:
Посмотреть, какая учебная неделя сейчас идет можно в еженедельном журнале посещения занятий. Они обычно всю неделю находятся у старосты и сдаются в деканат в конце недели. В журнале отмечается номер недели. Также эта информация есть на информационном стенде деканата факультета, а также Вашей кафедры.
Что означает числитель и знаменатель в расписании
Просто через неделю чередуется расписание, наверное так Часы удобнее распределять. На первой неделе верхнее расписание, на второй нижнее, потом верхнее, потом нижнее и так далее
Это не значит, что нижняя/верхняя будет всегда легче, они могут быть одинаково убогими
Смотри на примере по фото: допустим Группа «перан-92»
Несмотря на то, что у всех других групп в этот день есть первая пара, у них никогда ее нет. В этот день на любой неделе они приходят ко второй паре. Далее у них:
Показать полностью.
— на верхней неделе практикум по коммуникации, практика речи и культурные коды, то есть 3 пары
— на нижней неделе практикум по коммуникации, практика речи и ВСЕ. Кодов нет! Они только на верхней неделе, значит 2 пары
Не суди по тому, что только четыре дня, бывает и так. Значит повезло и нагрузка так распределилась, что этот день свободен
Про чёрные пары не могу сказать, что это значит, у меня такого не было
Как сокращать дроби: простые примеры с подробными решениями
Содержание:
В этой статье коротко предоставим информацию о том, как сокращать дроби. Сначала приведем немного теоретической части, а затем подкрепим ее решением практических задач.
Что означает сократить дробь
Как сокращаются дроби
Как привести дробь к несократимому виду
Обычно алгебраическое решение любой задачи по сокращению дробей сводится к получению равной дроби, но в несокращаемом виде. Чтобы получить несократимую дробь, ее делят на определенное число, которое называется наибольший общий делитель (сокращенно НОД):
Практически рассмотрим, используя дробь \frac < 6 > < 12 >. Ее можно сократить на НОД, который равняется 6. Тогда 6 : 6 = 1 и 12 : 6 = 2. Следовательно:
Последняя дробь является несократимой.
Следует обратить внимание, что в большинстве случаев если требуется выполнить сокращение дробей, то это значит выполнить до получения несократимой дроби.
Как сократить большую дробь
В качестве нового примера возьмем дробь 144192. Сначала найдем наибольший общий делитель для чисел 144 и 192. Для этого можно применить метод разложения на простые множители:
144 : 2 = 72 192 : 2 = 96
72 : 2 = 36 96 : 2 = 48
36 : 2 = 18 48 : 2 = 24
18 : 2 = 9 24 : 2 = 12
Тогда наибольшим общим множителем для данных чисел будет число 48 = 3 ∙ 2 ∙ 2 ∙ 2 ∙ 2.
Разделив исходную дробь на 48 получим несократимую дробь:
Разберем еще один способ, который позволяет сокращать числитель и знаменатель дроби последовательно на делитель, который без труда определяется по простейшим математическим признакам. Если требуется сократить дробь типа 40008 800, то можно сразу же определить, что здесь присутствует общий множитель 100, который можно вынести за скобку:
Далее невооруженным глазом заметно, что оба числа делятся на 2, а результат опять на 2 и т. д. В конечном итоге получаем несократимую дробь \frac < 5 > < 11 >= \frac < 4000 > < 8800 >. Теперь можно сказать, что наибольшим общим делителем для данной дроби было число 800.
В заключении заметим, что если знаменатель дроби представляет собой числитель, возведенный в квадрат, то такая дробь в несокращаемом виде всегда будет представлять собой: 1 – в числителе + число, значившееся числителем до сокращения, в знаменателе:
Числитель и знаменатель
Числитель дроби — это число, стоящее в записи обыкновенной дроби над дробной чертой, то есть сверху. Числитель показывает количество долей.
Знаменатель дроби — это число, стоящее в записи дроби под дробной чертой, то есть снизу. Знаменатель показывает, какие это доли и на сколько равных частей разделена единица.
Дробная черта — это горизонтальная черта в записи дроби, которая отделяет числитель и знаменатель друг от друга.
Вместе, числитель и знаменатель дроби, называются членами дроби.
Условились считать, что дробная черта означает деление верхнего числа на нижнее, поэтому:
Любую операцию деления можно записать в виде дроби. И наоборот, любую дробь можно записать в виде операции деления.
Как читать запись обыкновенных дробей
По этому правилу читаются все обыкновенные дроби.
Пример 1. Прочитайте дробь 
Пример 2. Прочитайте дробь 
Пример 3. Прочитайте дробь 
Как понять расписание в университете?
Как сокращать алгебраические дроби? С буквами и степенями. Примеры. Математика 8 класс.
Сведения о числителе/знаменателе
Заказчик
Богоявленский Юрий Анатольевич, зав. кафедры ИМО.. Эл.почта:
, Андреев Антон Александрович, программист.
Определение
Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:
Алгебраическая дробь содержит буквенные множители и степени.
Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.
Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.
Доли целого
Представим некий предмет, состоящий из нескольких, совершенно равных частей. Например, это может быть апельсин, состоящий из нескольких одинаковых долек.
Доля целого или доля – это каждая из равных частей, составляющих целый предмет.
Очевидно, что доли могут быть разные. Чтобы наглядно пояснить это утверждение, представим два яблока, одно из которых разрезано на две равные части, а второе – на четыре. Ясно, что размеры получившихся долей у разных яблок будут различаться.
Доли имеют свои названия, которые зависят от количества долей, составляющих целый предмет. Если предмет имеет две доли, то каждая из них будет определяться как одна вторая доля этого предмета; когда предмет состоит из трех долей, то каждая из них – одна третья и так далее.
Половина – одна вторая доля предмета.
Треть – одна третья доля предмета.
Четверть – одна четвертая доля предмета.
Чтобы сократить запись, ввели следующие обозначения долей: половина – 12 или 1/2; треть – 13 или 1/3; одна четвертая доля – 14 или 1/4 и так далее. Записи с горизонтальной чертой используются чаще.
Понятие доли естественно расширяется с предметов на величины. Так, можно использовать для измерения небольших предметов доли метра (треть или одна сотая), как одной из единиц измерения длины. Аналогичным образом можно применить доли других величин.
Видео-ответ
Это видео поможет разобраться
Аннотация проекта
Информация о типе недели часто требуется как студентам, так и преподавателям.
Цель проекта – разработать инструменты вычисления и визуализации типа недели.
Необходимо разработать алгоритм определения типа недели на все будущие годы, для чего опросить ответственных за это в учебном управлении ПетрГУ. Предусмотреть установку значения типа для первой недели.
Для визуализации типа разработать:
Дробные числа
Каждая дробь – это запись дробного числа, что по сути – просто «оболочка», визуализация смысловой нагрузки. Но все же для удобства мы объединяем понятия дроби и дробного числа, говоря просто – дробь.
Дроби на координатном луче
Все дробные числа, как и любое другое число, имеют свое уникальное месторасположение на координатном луче: существует однозначное соответствие между дробями и точками координатного луча.
Чтобы на координатном луче найти точку, обозначающую дробь mn, необходимо от начала координат отложить в положительном направлении m отрезков, длина каждого из которых составит 1n долю единичного отрезка. Отрезки можно получить, разделив единичный отрезок на n одинаковых частей.
Как пример, обозначим на координатном луче точку М, которая соответствует дроби 1410. Длина отрезка, концами которого является точка О и ближайшая точка, отмеченная маленьким штрихом, равна 110 доле единичного отрезка. Точка, соответствующая дроби 1410, расположена в удалении от начала координат на расстояние 14 таких отрезков.
Если дроби равны, т.е. им соответствует одно и то же дробное число, тогда эти дроби служат координатами одной и той же точки на координатном луче. К примеру, координатам в виде равных дробей 13, 26, 39, 515, 1133 соответствует одна и та же точка на координатном луче, располагающаяся на расстоянии трети единичного отрезка, отложенного от начала отсчета в положительном направлении.
Здесь работает тот же принцип, что и с целыми числами: на горизонтальном, направленном вправо координатном луче точка, которой соответствует большая дробь, разместится правее точки, которой соответствует меньшая дробь. И наоборот: точка, координата которой – меньшая дробь, будет располагаться левее точки, которой соответствует бОльшая координата.
Действия с дробями
Перечислим основные действия с дробями. В общем и целом, суть их та же, что имеют соответствующие действия с натуральными числами