Что означает четная и нечетная функция

Четные и нечетные функции

Функция называется четной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство

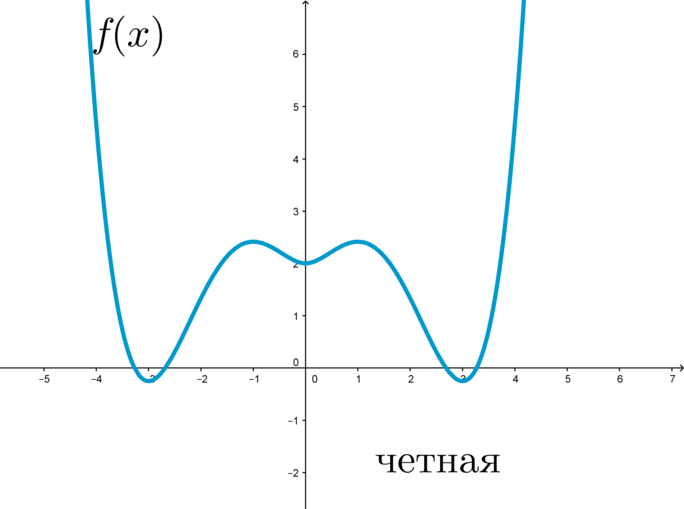
График четной функции симметричен относительно оси ординат.

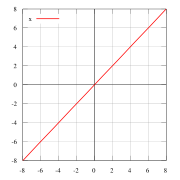
Например, — четные функции.

Функция называется нечетной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство

График нечетной функции симметричен относительно начала координат.

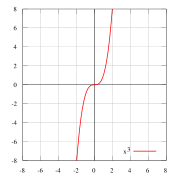
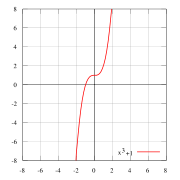
Например, — нечетные функции.

Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида.

Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задания:

1. Проверьте, является ли функция четной (нечетной).

Область определения функции

Проверим, является ли чётной или нечётной. Если функция четна. Если функция нечетна.

— значит, функция нечётная, её график симметричен относительно нуля.

2. Проверьте, является ли функция четной (нечетной)

Область определения: все действительные числа.

— чётная, как сумма двух чётных функций.

Её график симметричен относительно оси y.

3. Проверьте, является ли функция четной (нечетной).

Область определения функции симметрична относительно нуля.

— чётная, её график симметричен относительно оси y.

Источник

Четные и нечетные функции

Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.

Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.

Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.

Содержание

Определения

Свойства

Примеры

Нечётные функции

Чётные функции

Вариации и обобщения

Полезное

Смотреть что такое «Четные и нечетные функции» в других словарях:

Нечетные и четные функции — f(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия

Земляков — Земляков, Александр Николаевич Файл:Zemlyakov.jpg Александр Николаевич Земляков (17 апреля 1950(19500417), Бологое 1 января 2005, Черноголовка) математик,выдающийся советский и российский педагог, автор учебно педагогической… … Википедия

Земляков, Александр Николаевич — Александр Николаевич Земляков (17 апреля 1950(19500417), Бологое 1 января 2005, Черноголовка) математик, выдающийся советский и российский педагог, автор учебно педагогической литературы. Биография Закончил в 1967 году с золотой… … Википедия

Ряд Фурье — Добавление членов ряда Фурье … Википедия

H.265 — или HEVC (англ. High Efficiency Video Coding высокоэффективное видеокодирование) предполагаемая будущая рекомендация ITU T и проект стандарта ISO/IEC по сжатию видео с применением более эффективных алгоритмов по сравнению с H.264/MPEG… … Википедия

МАРЦИАН КАПЕЛЛА — МАРЦИАН КАПЕЛЛА (Martianus Minneius Felix Capeila) (2 я пол. 5 в. н. э.), латинский платоник, последний латинский выразитель «религии культуры» спасения через пайдейю. Известен как автор сочинения «О браке Филологии и Меркурия» (De nuptiis… … Античная философия

Link 16 — (TADIL J) тип военной тактической сети обмена данных, близкому к реальному. Используется США и странами НАТО. Является одной из составных частей семейства тактических сетей передачи данных TADIL (англ. Tactical Digital Information Link … Википедия

ЛАНДАУ ТЕОРЕМЫ — теоремы для регулярных в круге функций, устанавливающие нек рые связи между геометрич. свойствами производимого этими функциями конформного отображения и начальными коэффициентами представляющих их степенных рядов. В 1904 Э. Ландау показал [1],… … Математическая энциклопедия

Источник

Четная функция

Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.

Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.

Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.

Содержание

Определения

Свойства

Примеры

Нечётные функции

Чётные функции

Вариации и обобщения

Полезное

Смотреть что такое «Четная функция» в других словарях:

ЧЕТНАЯ ФУНКЦИЯ — функция, удовлетворяющая равенству f( x) = f(x) при всех x … Большой Энциклопедический словарь

ЧЕТНАЯ ФУНКЦИЯ — функция, не меняющая знак при изменении знака независимого переменного, т. е. функция, удовлетворяющая условию f( x)=f(x). График Ч. ф. симметричен относительно оси ординат … Математическая энциклопедия

ЧЕТНАЯ ФУНКЦИЯ — функция, удовлетворяющая равенству f( x) = f(x) при всех х … Естествознание. Энциклопедический словарь

чётная функция — функция, удовлетворяющая равенству f( х) = f(х) при всех х. * * * ЧЕТНАЯ ФУНКЦИЯ ЧЕТНАЯ ФУНКЦИЯ, функция, удовлетворяющая равенству f( x) = f(x) при всех x … Энциклопедический словарь

Многочлены Лежандра — Многочлен Лежандра многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов… … Википедия

Спектральная плотность — В статистической радиотехнике и физике при изучении детерминированных сигналов и случайных процессов широко используется их спектральное представление в виде спектральной плотности, которая базируется на преобразовании Фурье. Если процесс имеет… … Википедия

ЛЮКСЕМБУРГА НОРМА — функция где М(и) четная выпуклая функция, возрастающая при положительных U, М(u)>0 при u>0, G ограниченное замкнутое множество в Свойства этой нормы были изучены В. Люксембургом [1]. Л. н. эквивалентна норме Ор лича (см. Орлича… … Математическая энциклопедия

ВЕИЕРШТРАССА ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ — ф>тнкции, положенные К. Вейерштрассом в основу его общей теории эллиптических функций, излагавшейся им с 1862 на лекциях в Берлинском университете (см. [1], [2]). В отличие от более раннего построения теории эллиптич. функций, связанного с… … Математическая энциклопедия

Источник

Четные и нечетные функции

График четной функции симметричен относительно оси \(y\) :

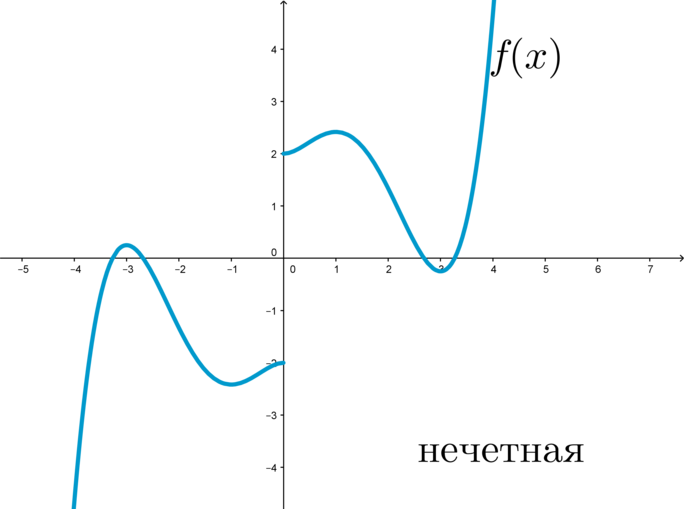
График нечетной функции симметричен относительно начала координат:

\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.

\(\blacktriangleright\) Некоторые свойства:

1) Произведение и частное двух функций одинаковой четности — четная функция.

2) Произведение и частное двух функций разной четности — нечетная функция.

3) Сумма и разность четных функций — четная функция.

4) Сумма и разность нечетных функций — нечетная функция.

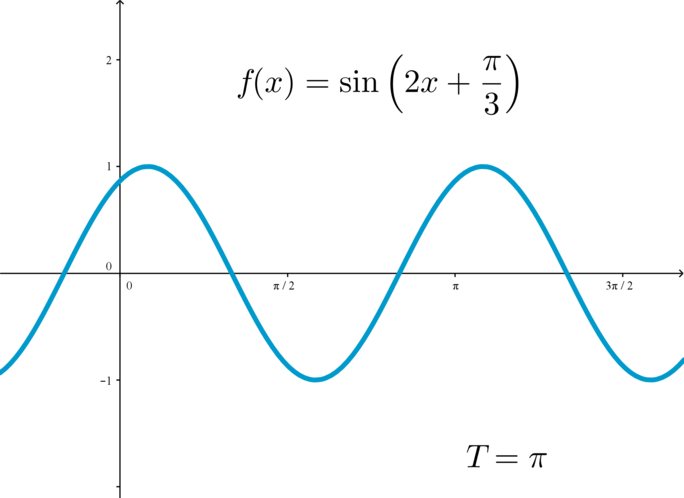
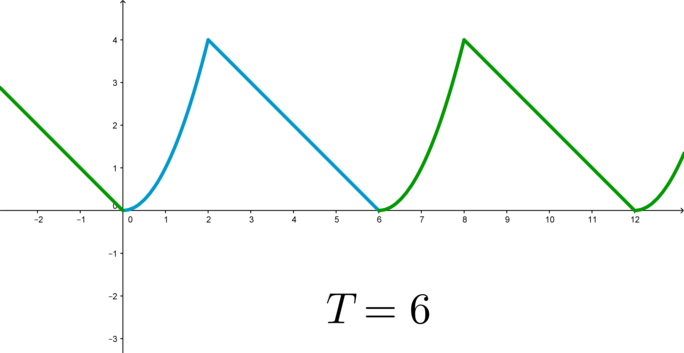
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:

При каких значениях параметра \(a\) уравнение

имеет единственное решение?

\[2\cdot 0+a\mathrm\,(\cos 0)+a^2=0 \quad \Rightarrow \quad a^2+a\mathrm\,1=0 \quad \Rightarrow \quad \left[ \begin\begin &a=0\\ &a=-\mathrm\,1 \end \end\right.\]

симметричен относительно начала координат.

Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)

\(\dfrac n2, n\in\mathbb\)

(Задача от подписчиков)

имеет хотя бы один корень.

(Задача от подписчиков)

имеет шесть различных решений.

Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.

1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \[D=a^2-16a+52>0\quad\Leftrightarrow\quad a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\]

2) Также нужно, чтобы оба корня были положительными (так как \(t>0\) ). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: \[\begin 12-a>0\\-(a-10)>0\end\quad\Leftrightarrow\quad a

Источник

Четность и нечетность функции. Период функции. Экстремумы функции

Содержание

Способы задания функции

Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.

Четная и нечетная функция

Функция является ни четной, ни нечетной и называется функцией общего вида, когда она не обладает симметрией относительно оси или начала координат.

Исследуем на четность нижеприведенную функцию:

Значит, функция f(x)=3x^<3>-7x^ <7>является нечетной.

Периодическая функция

f(x) > 0 на (x_<1>; x_<2>) \cup (x_<3>; +\infty )

f(x) на (-\infty; x_ <1>) \cup (x_<2>; x_ <3>)

Ограниченность функции

Возрастающая и убывающая функция

Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0 ).

а) Если при x > 0 четная функция возрастает, то убывает она при x

б) Когда при x > 0 четная функция убывает, то возрастает она при x

в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x

Экстремумы функции

Необходимое условие

Достаточное условие

Наибольшее и наименьшее значение функции на промежутке

Источник