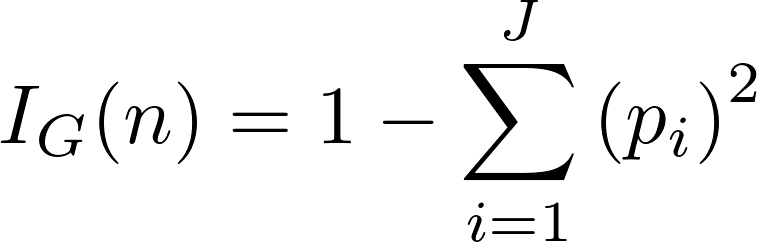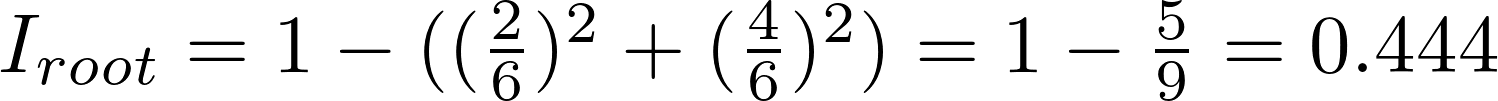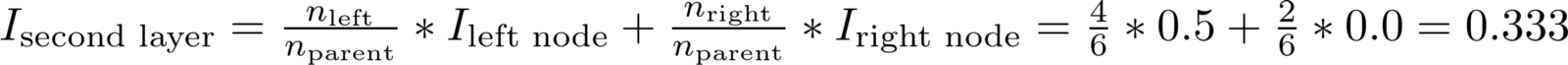Что отвечает в листьях регрессионное дерево
Деревья решений в Python с Scikit-Learn
Вступление
Дерево решений – это один из наиболее часто и широко используемых алгоритмов контролируемого машинного обучения, который может выполнять как регрессионные, так и классификационные задачи. Интуиция, лежащая в основе алгоритма дерева решений, проста, но в то же время очень мощна.
Для каждого атрибута в наборе данных алгоритм decision tree формирует узел, где наиболее важный атрибут помещается в корневой узел. Для оценки мы начинаем с корневого узла и продвигаемся вниз по дереву, следуя за соответствующим узлом, который удовлетворяет нашему условию или “решению”. Этот процесс продолжается до тех пор, пока не будет достигнут конечный узел, содержащий предсказание или результат дерева решений.
Поначалу это может показаться немного сложным, но вы, вероятно, не осознаете, что всю свою жизнь использовали деревья решений для принятия решений, даже не подозревая об этом. Представьте себе ситуацию, когда человек просит вас одолжить ему машину на день, и вы должны принять решение, одолжить ему машину или нет. Есть несколько факторов, которые помогают определить ваше решение, некоторые из которых были перечислены ниже:
Дерево решений для вышеупомянутого сценария выглядит следующим образом:
Преимущества деревьев решений
Использование деревьев решений для прогнозного анализа имеет ряд преимуществ:
Реализация деревьев решений с помощью Python Scikit Learn
Примечание : Задачи классификации и регрессии были выполнены в записной книжке Jupyter IPython.
1. Дерево решений для классификации
В этом разделе мы будем предсказывать, является ли банкнота подлинной или поддельной в зависимости от четырех различных атрибутов изображения банкноты. К атрибутам относятся дисперсия вейвлет-преобразованного изображения, эксцесс изображения, энтропия и асимметрия изображения.
Набор данных
Набор данных для этой задачи можно загрузить по этой ссылке:
Набор данных для этой задачи можно загрузить по этой ссылке:
Для получения более подробной информации об этом наборе данных ознакомьтесь с UCI ML repo для этого набора данных.
Остальные шаги по реализации этого алгоритма в Scikit-Learn идентичны любой типичной задаче машинного обучения: мы импортируем библиотеки и наборы данных, выполняем некоторый анализ данных, разделяем данные на обучающие и тестовые наборы, обучаем алгоритм, делаем прогнозы и, наконец, оцениваем производительность алгоритма на нашем наборе данных.
Импорт библиотек
Следующий сценарий импортирует необходимые библиотеки:
Деревья решений: общие принципы
Деревья решений — один из методов автоматического анализа данных. Разбираем общие принципы работы и области применения.
Деревья решений являются одним из наиболее эффективных инструментов интеллектуального анализа данных и предсказательной аналитики, которые позволяют решать задачи классификации и регрессии.
Поскольку правила в деревьях решений получаются путём обобщения множества отдельных наблюдений (обучающих примеров), описывающих предметную область, то по аналогии с соответствующим методом логического вывода их называют индуктивными правилами, а сам процесс обучения — индукцией деревьев решений.
В обучающем множестве для примеров должно быть задано целевое значение, т.к. деревья решений являются моделями, строящимися на основе обучения с учителем. При этом, если целевая переменная дискретная (метка класса), то модель называют деревом классификации, а если непрерывная, то деревом регрессии.
Основополагающие идеи, послужившие толчком к появлению и развитию деревьев решений, были заложены в 1950-х годах в области исследований моделирования человеческого поведения с помощью компьютерных систем. Среди них следует выделить работы К. Ховеленда «Компьютерное моделирование мышления»[1] и Е. Ханта и др. «Эксперименты по индукции»[2].
Дальнейшее развитие деревьев решений как самообучающихся моделей для анализа данных связано с именами Джона Р. Куинлена[3], который разработал алгоритм ID3 и его усовершенствованные модификации С4.5 и С5.0, а так же Лео Бреймана[4], который предложил алгоритм CART и метод случайного леса.
Терминология
Введем в рассмотрение основные понятия, используемые в теории деревьев решений.
| Название | Описание |
|---|---|
| Объект | Пример, шаблон, наблюдение |
| Атрибут | Признак, независимая переменная, свойство |
| Целевая переменная | Зависимая переменная, метка класса |
| Узел | Внутренний узел дерева, узел проверки |
| Корневой узел | Начальный узел дерева решений |
| Лист | Конечный узел дерева, узел решения, терминальный узел |
| Решающее правило | Условие в узле, проверка |
Структура дерева решений
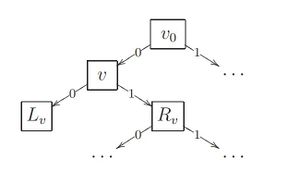
Собственно, само дерево решений — это метод представления решающих правил в иерархической структуре, состоящей из элементов двух типов — узлов (node) и листьев (leaf). В узлах находятся решающие правила и производится проверка соответствия примеров этому правилу по какому-либо атрибуту обучающего множества.
В простейшем случае, в результате проверки, множество примеров, попавших в узел, разбивается на два подмножества, в одно из которых попадают примеры, удовлетворяющие правилу, а в другое — не удовлетворяющие.
Затем к каждому подмножеству вновь применяется правило и процедура рекурсивно повторяется пока не будет достигнуто некоторое условие остановки алгоритма. В результате в последнем узле проверка и разбиение не производится и он объявляется листом. Лист определяет решение для каждого попавшего в него примера. Для дерева классификации — это класс, ассоциируемый с узлом, а для дерева регрессии — соответствующий листу модальный интервал целевой переменной.
Таким образом, в отличие от узла, в листе содержится не правило, а подмножество объектов, удовлетворяющих всем правилам ветви, которая заканчивается данным листом.
Очевидно, чтобы попасть в лист, пример должен удовлетворять всем правилам, лежащим на пути к этому листу. Поскольку путь в дереве к каждому листу единственный, то и каждый пример может попасть только в один лист, что обеспечивает единственность решения.
Задачи
Основная сфера применения деревьев решений — поддержка процессов принятия управленческих решений, используемая в статистике, анализе данных и машинном обучении. Задачами, решаемыми с помощью данного аппарата, являются:
Процесс построения
Процесс построения деревьев решений заключается в последовательном, рекурсивном разбиении обучающего множества на подмножества с применением решающих правил в узлах. Процесс разбиения продолжается до тех пор, пока все узлы в конце всех ветвей не будут объявлены листьями. Объявление узла листом может произойти естественным образом (когда он будет содержать единственный объект, или объекты только одного класса), или по достижении некоторого условия остановки, задаваемого пользователем (например, минимально допустимое число примеров в узле или максимальная глубина дерева).
Алгоритмы построения деревьев решений относят к категории так называемых жадных алгоритмов. Жадными называются алгоритмы, которые допускают, что локально-оптимальные решения на каждом шаге (разбиения в узлах), приводят к оптимальному итоговому решению. В случае деревьев решений это означает, что если один раз был выбран атрибут, и по нему было произведено разбиение на подмножества, то алгоритм не может вернуться назад и выбрать другой атрибут, который дал бы лучшее итоговое разбиение. Поэтому на этапе построения нельзя сказать обеспечит ли выбранный атрибут, в конечном итоге, оптимальное разбиение.
Описанная выше процедура лежит в основе многих современных алгоритмов построения деревьев решений. Очевидно, что при использовании данной методики, построение дерева решений будет происходить сверху вниз (от корневого узла к листьям).
В настоящее время разработано значительное число алгоритмов обучения деревья решений: ID3, CART, C4.5, C5.0, NewId, ITrule, CHAID, CN2 и т.д. Но наибольшее распространение и популярность получили следующие:
Основные этапы построения
В ходе построения дерева решений нужно решить несколько основных проблем, с каждой из которых связан соответствующий шаг процесса обучения:
Рассмотрим эти этапы ниже.
Выбор атрибута разбиения
При формировании правила для разбиения в очередном узле дерева необходимо выбрать атрибут, по которому это будет сделано. Общее правило для этого можно сформулировать следующим образом: выбранный атрибут должен разбить множество наблюдений в узле так, чтобы результирующие подмножества содержали примеры с одинаковыми метками класса, или были максимально приближены к этому, т.е. количество объектов из других классов («примесей») в каждом из этих множеств было как можно меньше. Для этого были выбраны различные критерии, наиболее популярными из которых стали теоретико-информационный и статистический.
Теоретико-информационный критерий
Как следует из названия, критерий основан на понятиях теории информации, а именно — информационной энтропии.
где n — число классов в исходном подмножестве, N_i — число примеров i-го класса, N — общее число примеров в подмножестве.
Таким образом, лучшим атрибутом разбиения A_j будет тот, который обеспечит максимальное снижение энтропии результирующего подмножества относительно родительского. На практике, однако, говорят не об энтропии, а о величине, обратной ей, которая называется информацией. Тогда лучшим атрибутом разбиения будет тот, который обеспечит максимальный прирост информации результирующего узла относительно исходного:
Статистический подход
В основе статистического подхода лежит использование индекса Джини (назван в честь итальянского статистика и экономиста Коррадо Джини). Статистический смысл данного показателя в том, что он показывает — насколько часто случайно выбранный пример обучающего множества будет распознан неправильно, при условии, что целевые значения в этом множестве были взяты из определённого статистического распределения.
Таким образом индекс Джини фактически показывает расстояние между двумя распределениями — распределением целевых значений, и распределением предсказаний модели. Очевидно, что чем меньше данное расстояние, тем лучше работает модель.
Индекс Джини может быть рассчитан по формуле:
где Q — результирующее множество, n — число классов в нём, p_i — вероятность i-го класса (выраженная как относительная частота примеров соответствующего класса). Очевидно, что данный показатель меняется от 0 до 1. При этом он равен 0, если все примеры Q относятся к одному классу, и равен 1, когда классы представлены в равных пропорциях и равновероятны. Тогда лучшим будет то разбиение, для которого значение индекса Джини будут минимальным.
Критерий остановки алгоритма
Теоретически, алгоритм обучения дерева решений будет работать до тех пор, пока в результате не будут получены абсолютно «чистые» подмножества, в каждом из которых будут примеры одного класса. Правда, возможно при этом будет построено дерево, в котором для каждого примера будет создан отдельный лист. Очевидно, что такое дерево окажется бесполезным, поскольку оно будет переобученным — каждому примеру будет соответствовать свой уникальный путь в дереве, а следовательно, и набор правил, актуальный только для данного примера.
Переобучение в случае дерева решений ведёт к тем же последствиям, что и для нейронной сети — точное распознавание примеров, участвующих в обучении и полная несостоятельность на новых данных. Кроме этого, переобученные деревья имеют очень сложную структуру, и поэтому их сложно интерпретировать.
Очевидным решением проблемы является принудительная остановка построения дерева, пока оно не стало переобученным. Для этого разработаны следующие подходы.
Все перечисленные подходы являются эвристическими, т.е. не гарантируют лучшего результата или вообще работают только в каких-то частных случаях. Поэтому к их использованию следует подходить с осторожностью. Каких-либо обоснованных рекомендаций по тому, какой метод лучше работает, в настоящее время тоже не существует. Поэтому аналитикам приходится использовать метод проб и ошибок.
Отсечение ветвей
Как было отмечено выше, если «рост» дерева не ограничить, то в результате будет построено сложное дерево с большим числом узлов и листьев. Как следствие оно будет трудно интерпретируемым. В то же время решающие правила в таких деревьях, создающие узлы, в которые попадают два-три примера, оказываются малозначимыми с практической точки зрения.
Гораздо предпочтительнее иметь дерево, состоящее из малого количества узлов, которым бы соответствовало большое число примеров из обучающей выборки. Поэтому представляет интерес подход, альтернативный ранней остановке — построить все возможные деревья и выбрать то из них, которое при разумной глубине обеспечивает приемлемый уровень ошибки распознавания, т.е. найти наиболее выгодный баланс между сложностью и точностью дерева.
К сожалению, это задача относится к классу NP-полных задач, что было показано Л. Хайфилем (L. Hyafill) и Р. Ривестом (R. Rivest), и, как известно, этот класс задач не имеет эффективных методов решения.
Альтернативным подходом является так называемое отсечение ветвей (pruning). Он содержит следующие шаги:
Отсечение ветвей, очевидно, производится в направлении, противоположном направлению роста дерева, т.е. снизу вверх, путём последовательного преобразования узлов в листья. Преимуществом отсечения ветвей по сравнению с ранней остановкой является возможность поиска оптимального соотношения между точностью и понятностью дерева. Недостатком является большее время обучения из-за необходимости сначала построить полное дерево.
Извлечение правил
Иногда даже упрощённое дерево решений все ещё является слишком сложным для визуального восприятия и интерпретации. В этом случае может оказаться полезным извлечь из дерева решающие правила и организовать их в наборы, описывающие классы.
Для извлечения правил нужно отследить все пути от корневого узла к листьям дерева. Каждый такой путь даст правило, состоящее из множества условий, представляющих собой проверку в каждом узле пути.
Визуализация сложных деревьев решений в виде решающих правил вместо иерархической структуры из узлов и листьев может оказаться более удобной для визуального восприятия.
Преимущества алгоритма
Рассмотрев основные проблемы, возникающие при построении деревьев, было бы несправедливо не упомянуть об их достоинствах:
В силу этих и многих других причин, деревья решений являются важным инструментом в работе каждого специалиста, занимающегося анализом данных.
Области применения
Модули для построения и исследования деревьев решений входят в состав большинства аналитических платформ. Они являются удобным инструментом в системах поддержки принятия решений и интеллектуального анализа данных.
Деревья решений успешно применяются на практике в следующих областях:
Это далеко не полный список областей где можно использовать деревья решений. Вместе с анализом данных деревья решений постоянно расширяют круг своего использования, становясь важным инструментом управления бизнес-процессами и поддержки принятия решений.
Дерево решений и случайный лес
Дерево решений — логический алгоритм классификации, решающий задачи классификации и регрессии. Представляет собой объединение логических условий в структуру дерева.
Содержание
Дерево решений [ править ]
Информативность ветвления [ править ]
| Определение: |
| Частотная оценка вероятности класса [math]y[/math] в вершине [math]v \in V_<внутр>[/math] : [math]p_y = P(y | x \in U) = \frac<1> <|U|>\sum\nolimits_ |
Примерами мер неопределенности распределения являются:
Теперь определим суммарную неопределенность распределения в разбиении.
Информационный выигрыш от разбиения определяется как изменение неопределенности в системе.
Рекурсивный алгоритм построения бинарного дерева решений ID3 [ править ]
Редукция решающих деревьев [ править ]
Суть редукции (англ. pruning) состоит в удалении поддеревьев, имеющих недостаточную статистическую надёжность. При этом дерево перестаёт безошибочно классифицировать обучающую выборку, зато качество классификации новых объектов, как правило, улучшается. Рассмотрим наиболее простые варианты редукции.
Предредукция [ править ]
Постредукция [ править ]
Постредукция (англ. post-pruning) просматривает все внутренние вершины дерева и заменяет отдельные вершины либо одной из дочерних вершин (при этом вторая дочерняя удаляется), либо терминальной вершиной. Процесс замен продолжается до тех пор, пока в дереве остаются вершины, удовлетворяющие критерию замены.
Критерием замены является сокращение числа ошибок на контрольной выборке, отобранной заранее, и не участвовавшей в обучении дерева. Стандартная рекомендация — оставлять в контроле около 30% объектов.
Эти величины сравниваются, и в зависимости от того, какая из них оказалась минимальной, принимается, соответственно, одно из четырёх решений:
Алгоритмы построения деревьев решения [ править ]
Недостатки рассмотренного алгоритма ID3:
Алгоритм CART (англ. Classification And Regression Trees) [ править ]
Алгоритм C4.5 [ править ]
Случайный лес [ править ]
Случайный лес — один из примеров объединения классификаторов в ансамбль.
Алгоритм построения случайного леса, состоящего из [math]N[/math] деревьев на основе обучающей выборки [math]X[/math] такой:
Таким образом, случайный лес — бэггинг над решающими деревьями, при обучении которых для каждого разбиения признаки выбираются из некоторого случайного подмножества признаков.
Примеры кода [ править ]
Примеры на языке Python [ править ]
Так, в этом примере создается бэггинг ансамбль из классификаторов KNeighborsClassifier, каждый из которых обучен на случайных подмножествах из 50% объектов из обучающей выборки, и 50% случайно выбранных признаков.
Пример использования классификатора на случайном лесе: Полную версию кода можно найти здесь
Результат классификации показан на рисунке.
Пример на языке Scala [ править ]
Пример классификации датасета и вычисления F1 меры [1] используя smile.classification.cart [2] :
Пример на языке Java [ править ]
Пример классификации с применением weka.classifiers.trees.RandomForest [3]
Пример на языке R [ править ]
Деревья решений [ править ]
Случайный лес [ править ]
Для создания случайного леса необходимо импортировать пакет randomForest
Реализация и разбор алгоритма «случайный лес» на Python
Использование готовых библиотек, таких как Scikit-Learn, позволяет легко реализовать на Python сотни алгоритмов машинного обучения.
В этой статье мы научимся создать и использовать алгоритм «случайный лес» (Random Forest) на Python. Помимо непосредственного изучения кода, мы постараемся понять принципы работы модели. Этот алгоритм составлен из множества деревьев решений, поэтому сначала мы разберёмся, как одно такое дерево решает проблему классификации. После этого с помощью алгоритма решим проблему, используя набор реальных научных данных. Весь код, используемый в этой статье, доступен на GitHub в Jupyter Notebook.
Как работает дерево решений
Дерево решений — интуитивно понятная базовая единица алгоритма случайный лес. Мы можем рассматривать его как серию вопросов да/нет о входных данных. В конечном итоге вопросы приводят к предсказанию определённого класса (или величины в случае регрессии). Это интерпретируемая модель, так как решения принимаются так же, как и человеком: мы задаём вопросы о доступных данных до тех пор, пока не приходим к определённому решению (в идеальном мире).
Базовая идея дерева решений заключается в формировании запросов, с которыми алгоритм обращается к данным. При использовании алгоритма CART вопросы (также называемые разделением узлов) определяются таким образом, чтобы ответы вели к уменьшению загрязнения Джини (Gini Impurity). Это означает, что дерево решений формирует узлы, содержащие большое количество образцов (из набора исходных данных), принадлежащих к одному классу. Алгоритм старается обнаружить параметры со сходными значениями.
Подробности, касающиеся загрязнения Джини, мы обсудим позже, а сейчас давайте создадим дерево решений, чтобы понять, как работает этот алгоритм.
Дерево решений для простой задачи
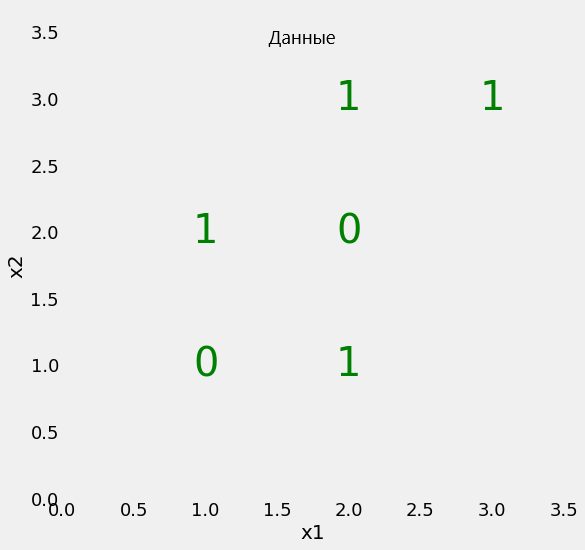
Начнём с проблемы простой бинарной классификации, изображённой на диаграмме.
Наш набор данных имеет всего два параметра (две заданные переменные), x1 и x2, а также 6 образцов, несущих эти параметры. Образцы разделены метками на два класса. Хотя это простая задача, линейно классы разделить невозможно. Это означает, что мы не можем нарисовать на предложенной плоскости прямую линию, которая отделит один класс от другого.
В то же время мы можем разбить плоскость на участки (узлы) несколькими прямыми линиями. Именно это делает дерево решений в процессе тренировки. По сути дерево решений — нелинейная модель, создаваемая с помощью множества линейных ограничителей.
Мы используем Scikit-Learn, чтобы создать дерево решений и обучить ( fit ) его, используя наши данные.
Во время обучения мы используем и параметры, и метки, чтобы модель научилась сортировать данные на основе параметров. Для таких простых задач не используется тестовый набор данных. Но при тестировании модели мы сообщаем только параметры и сравниваем результат сортировки с теми метками, которые ожидали получить.
Можно проверить точность предсказаний нашей модели:
Разумеется, мы получим точность 100 %, так как сообщили модели правильные ответы ( y ) и не ограничивали глубину дерева. Но следует помнить, что подобная подгонка дерева решений под тренировочные данные может спровоцировать переобучение модели.
Визуализация дерева решений
Что же на самом деле происходит при обучении дерева решений? Хороший способ понять это — визуализация модели при помощи соответствующей функции Scikit-Learn (подробнее функция рассматривается в данной статье).
Во всех узлах, кроме листьев (цветные узлы без исходящих связей), содержится 5 частей:
Листья не содержат вопроса, так как являются финальными прогнозируемыми значениями классификации. Чтобы обработать новый элемент набора данных, нужно просто двигаться вниз по дереву, используя параметры элемента для ответов на вопросы. В финале вы доберётесь до одного из листьев, значение Class которого и будет прогнозируемым классом элемента.
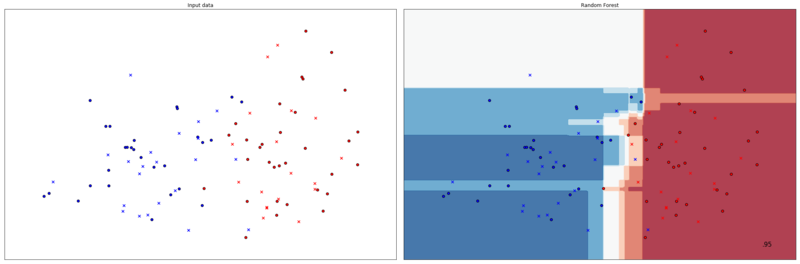
Чтобы взглянуть на дерево решений под другим углом, мы спроецируем разделения модели на исходные данные.
Каждое разделение отображается одной линией, разделяющей образцы данных на узлы в соответствии со значением параметров. Поскольку максимальная глубина дерева не ограничена, разделение размещает каждый элемент в узел, содержащий только элементы того же класса. Позже мы рассмотрим, как идеальное разделение обучающих данных может привести к переобучению.
Загрязнение Джини
Теперь самое время рассмотреть концепцию загрязнения Джини (математика не так уж страшна, как кажется). Загрязнение Джини — вероятность неверной маркировки в узле случайно выбранного образца. К примеру, в верхнем (корневом) узле вероятность неверной классификации образца равна 44.4 %. Это можно вычислить с помощью уравнения:
Загрязнение Джини узла n равно 1 минус сумма отношений класса к общему количеству образцов pi, возведённых в квадрат, для каждого из множества классов J (в нашем случае это всего 2 класса). Звучит сложно, поэтому покажем, как вычисляется загрязнение Джини для корневого узла:
В каждом узле дерево решений ищет такое значение определённого параметра, которое приведёт к максимальному уменьшению загрязнения Джини. В качестве альтернативы для разделения узлов также можно использовать концепцию накопления информации.
Затем процесс разделения повторяется с использованием «жадной», рекурсивной процедуры, пока дерево не достигнет максимальной глубины или в каждом узле не останутся только образцы одного класса. Общевзвешенное загрязнение Джини должно уменьшаться с каждым уровнем. В нашем случае на втором уровне оно составит 0.333:
Удельный вес загрязнения Джини для каждого узла равен отношению количества образцов, обработанных этим узлом, к количеству обработанных родительским узлом. Вы можете самостоятельно рассчитать загрязнение Джини для последующих уровней дерева и отдельных узлов, используя данные визуализации. Таким образом, эффективная модель строится на базовых математических операциях.
В итоге общевзвешенное загрязнение Джини последнего слоя сводится к нулю. Это значит, что каждый конечный узел содержит только образцы одного класса, и случайно выбранный образец не может быть неверно классифицирован. Звучит отлично, но помните, что это может быть сигналом того, что модель переобучена. Это происходит, потому что узлы смоделированы только на обучающих данных.
Переобучение, или почему лес лучше одного дерева
Может создаться впечатление, что для решения задачи хватило бы и одного дерева решений. Ведь эта модель не делает ошибок. Однако важно помнить, что алгоритм безошибочно отсортировал только тренировочные данные. Этого и следовало ожидать, поскольку мы указали верные ответы и не ограничили глубину дерева (количество слоёв). Но цель машинного обучения состоит в том, чтобы научить алгоритм обобщать полученную информацию и верно обрабатывать новые, ранее не встречавшиеся данные.
Переобучение происходит, когда мы используем очень гибкую модель (с высокой вместимостью), которая просто запоминает обучающий набор данных, подгоняя узлы под него. Проблема в том, что такая модель выявляет не только закономерности в данных, но и любой присутствующий в них шум. Такую гибкую модель часто называют высоковариативной, поскольку параметры, формирующиеся в процессе обучения (такие как структура дерева решений) будут значительно варьироваться в зависимости от обучающего набора данных.
С другой стороны, у недостаточно гибкой модели будет высокий уровень погрешности, поскольку она делает предположения относительно тренировочных данных (модель смещается в сторону предвзятых предположений о данных). К примеру, линейный классификатор предполагает, что данные распределены линейно. Из-за этого он не обладает достаточной гибкостью для соответствия нелинейным структурам. Ригидная модель может оказаться недостаточно ёмкой даже для соответствия тренировочным данным.
В обоих случаях — и при высокой вариативности, и при высокой погрешности — модель не сможет эффективно обрабатывать новые данные.
Поиск баланса между излишней и недостаточной гибкостью модели является ключевой концепцией машинного обучения и называется компромиссом между вариативностью и погрешностью (bias-variance tradeoff).
Алгоритм дерева решений переобучается, если не ограничить его максимальную глубину. Он обладает неограниченной гибкостью и может разрастаться, пока не достигнет состояния идеальной классификации, в которой каждому образцу из набора данных будет соответствовать один лист. Если вернуться назад к созданию дерева и ограничить его глубину двумя слоями (сделав только одно разделение), классификация больше не будет на 100 % верной. Мы уменьшаем вариативность за счёт увеличения погрешности.
В качестве альтернативы ограничению глубины, которое ведёт к уменьшению вариативности (хорошо) и увеличению погрешности (плохо), мы можем собрать множество деревьев в единую модель. Это и будет классификатор на основе комитета деревьев принятия решений или просто «случайный лес».
Случайный лес
Случайный лес — модель, состоящая из множества деревьев решений. Вместо того,чтобы просто усреднять прогнозы разных деревьев (такая концепция называется просто «лес»), эта модель использует две ключевые концепции, которые и делают этот лес случайным.
Случайная выборка тренировочных образцов
В процессе тренировки каждое дерево случайного леса учится на случайном образце из набора данных. Выборка образцов происходит с возмещением (в статистике этот метод называется бутстреппинг, bootstrapping). Это даёт возможность повторно использовать образцы одним и тем же деревом. Хотя каждое дерево может быть высоковариативным по отношению к определённому набору тренировочных данных, обучение деревьев на разных наборах образцов позволяет понизить общую вариативность леса, не жертвуя точностью.
При тестировании результат выводится путём усреднения прогнозов, полученных от каждого дерева. Подход, при котором каждый обучающийся элемент получает собственный набор обучающих данных (с помощью бутстреппинга), после чего результат усредняется, называется бэггинг (bagging, от bootstrap aggregating).
Случайные наборы параметров для разделения узлов
Вторая базовая концепция случайного леса заключается в использовании определённой выборки параметров образца для разделения каждого узла в каждом отдельном дереве. Обычно размер выборки равен квадратному корню из общего числа параметров. То есть, если каждый образец набора данных содержит 16 параметров, то в каждом отдельном узле будет использовано 4. Хотя обучение случайного леса можно провести и с полным набором параметров, как это обычно делается при регрессии. Этот параметр можно настроить в реализации случайного леса в Scikit-Learn.
Случайный лес сочетает сотни или тысячи деревьев принятия решений, обучая каждое на отдельной выборке данных, разделяя узлы в каждом дереве с использованием ограниченного набора параметров. Итоговый прогноз делается путём усреднения прогнозов от всех деревьев.
Чтобы лучше понять преимущество случайного леса, представьте следующий сценарий: вам нужно решить, поднимется ли цена акций определённой компании. У вас есть доступ к дюжине аналитиков, изначально не знакомых с делами этой компании. Каждый из аналитиков характеризуется низкой степенью погрешности, так как не делает каких-либо предположений. Кроме того, они могут получать новые данные из новостных источников.
Трудность задачи в том, что новости, помимо реальных сигналов, могут содержать шум. Поскольку предсказания аналитиков базируются исключительно на данных — обладают высокой гибкостью — они могут быть искажены не относящейся к делу информацией. Аналитики могут прийти к разным заключениям, исходя из одних и тех же данных. Кроме того, каждый аналитик старается делать прогнозы, максимально коррелирующие с полученными отчётами (высокая вариативность) и предсказания могут значительно различаться при разных наборах новостных источников.
Поэтому нужно не опираться на решение какого-то одного аналитика, а собрать вместе их прогнозы. Более того, как и при использовании случайного леса, нужно разрешить каждому аналитику доступ только к определённым новостным источникам, в надежде на то, что эффекты шумов будут нейтрализованы выборкой. В реальной жизни мы полагаемся на множество источников (никогда не доверяйте единственному обзору на Amazon). Интуитивно нам близка не только идея дерева решений, но и комбинирование их в случайный лес.
Алгоритм Random Forest на практике
Настало время реализовать алгоритм случайного леса на языке Python с использованием Scikit-Learn. Вместо того чтобы работать над элементарной теоретической задачей, мы используем реальный набор данных, разбив его на обучающий и тестовый сеты. Тестовые данные мы используем для оценки того, насколько хорошо наша модель справляется с новыми данными, что поможет нам выяснить уровень переобучения.
Набор данных
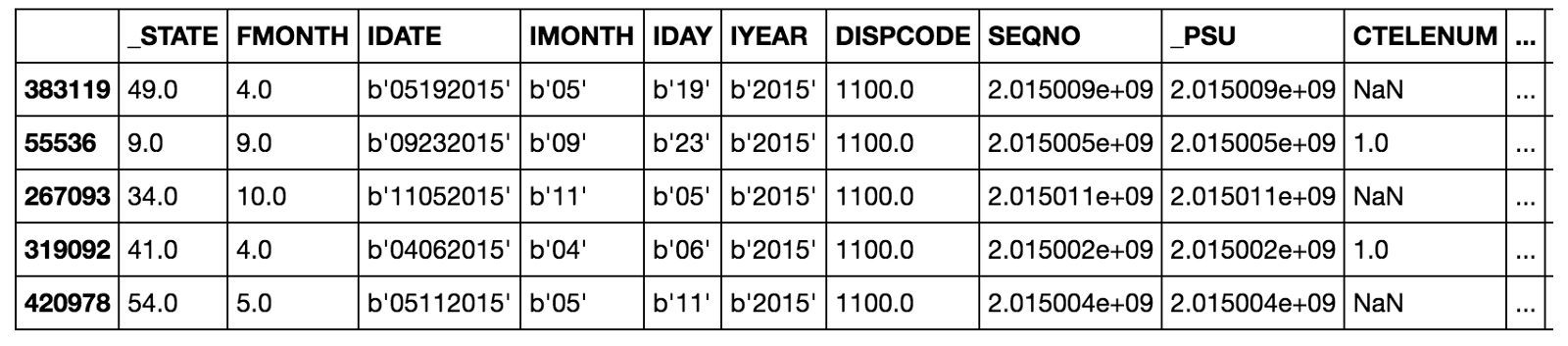
Мы попробуем рассчитать состояние здоровья пациентов в бинарной системе координат. В качестве параметров мы используем социально-экономические и персональные характеристики субъектов. В качестве меток мы используем 0 для плохого здоровья и 1 для хорошего. Этот набор данных был собран Центром по Контролю и Предотвращению Заболеваний и размещён в свободном доступе.
Как правило 80 % работы над научным проектом заключается в изучении, очистке и синтезировании параметров из сырых данных (подробнее узнать можно здесь). Однако в этой статье мы сосредоточимся на построении модели.
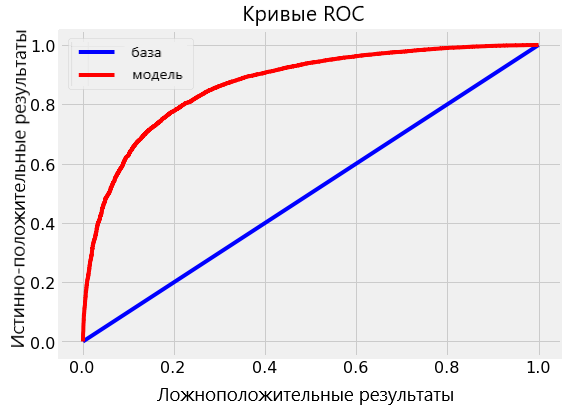
В данном примере мы сталкиваемся с задачей несбалансированной классификации, поэтому простой параметр точности модели не отобразит истинной её производительности. Вместо этого мы используем площадь под кривой операционных характеристик приёмника (ROC AUC), измерив от 0 (в худшем случае) до 1 (в лучшем случае) со случайным прогнозом на уровне 0,5. Мы также можем построить указанную кривую, чтобы проанализировать модель.
В этом Jupyter notebook содержатся реализации и дерева решений, и случайного леса, но здесь мы сфокусируемся на последнем. После получения данных мы можем создать и обучить этот алгоритм следующим образом:
После нескольких минут обучения модель будет готова выдавать прогнозы для тестовых данных:
Мы рассчитаем прогнозы классификации ( predict ) наряду с прогностической вероятностью ( predict_proba ), чтобы вычислить ROC AUC.
Результаты
Итоговое тестирование ROC AUC для случайного леса составило 0.87, в то время как для единичного дерева с неограниченной глубиной — 0.67. Если вернуться к результатам обработки тренировочных данных, обе модели покажут эффективность, равную 1.00 на ROC AUC. Этого и следовало ожидать, ведь мы предоставили готовые ответы и не ограничивали максимальную глубину каждого дерева.
Несмотря на то, что случайный лес переобучен (показывает на тренировочных данных лучшую производительность, чем на тестовых), он всё же гораздо больше способен к обобщениям, чем одиночное дерево. При низкой вариативности (хорошо) случайный лес наследует от одиночного дерева решений низкую склонность к погрешности (что тоже хорошо).
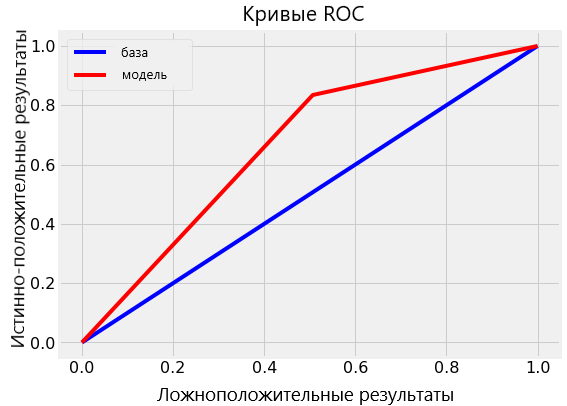
Мы можем визуализовать кривую ROC для одиночного дерева (верхняя диаграмма) и для случайного леса в целом (нижняя диаграмма). Кривая лучшей модели стремится вверх и влево:
Случайный лес значительно превосходит по точности одиночное дерево.
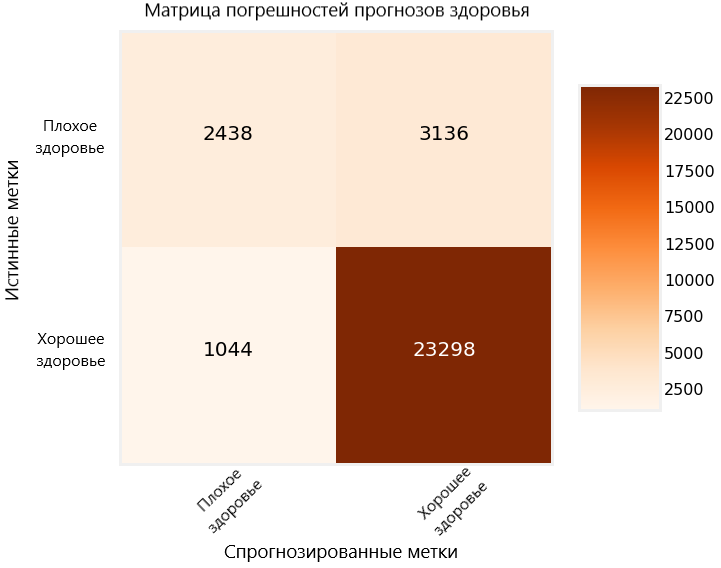
Ещё один способ оценить эффективность построенной модели — матрица погрешностей для тестовых прогнозов.
На диаграмме верные прогнозы, сделанные моделью, отображаются в верхнем левом углу и в нижнем правом, а неверные в нижнем левом и верхнем правом. Подобные диаграммы мы можем использовать, чтобы оценить, достаточно ли проработана наша модель и готова ли она к релизу.
Значимость параметра
Значимость параметра в случайном лесу — это суммарное уменьшение загрязнения Джини во всех узлах, использующих этот параметр для разделения. Мы можем использовать это значение для определения опытным путём, какие переменные более всего принимаются во внимание нашей моделью. Мы можем рассчитать значимость параметров в уже обученной модели и экспортировать результаты этих вычислений в Pandas DataFrame следующим образом:
Рассматриваемая величина может также использоваться для синтезирования дополнительных параметров, объединяющих несколько наиболее важных. При отборе параметров их значимость может указать на те, которые можно удалить из набора данных без ущерба производительности модели.
Визуализация единичного дерева леса
Мы также можем визуализовать единичное дерево случайного леса. В данном случае нам придётся ограничить его глубину, иначе оно может оказаться слишком большим для преобразования в изображение. Для этого изображения глубина была ограничена до 6 уровней. Результат всё равно слишком велик, однако, внимательно его изучив, мы можем понять, как работает наша модель.
Следующие шаги
Следующим шагом будет оптимизация случайного леса, которую можно выполнить через случайный поиск, используя RandomizedSearchCV в Scikit-Learn. Оптимизация подразумевает поиск лучших гиперпараметров для модели на текущем наборе данных. Лучшие гиперпараметры будут зависеть от набора данных, поэтому нам придётся проделывать оптимизацию (настройку модели) отдельно для каждого набора.
Можно рассматривать настройку модели как поиск лучших установок для алгоритма машинного обучения. Примеры параметров, которые можно оптимизировать: количество деревьев, их максимальная глубина, максимальное количество параметров, принимаемых каждым узлом, максимальное количество образцов в листьях.
Реализацию случайного поиска для оптимизации модели можно изучить в Jupyter Notebook.
Полностью рабочий образец кода
Приведённый ниже код создан с помощью repl.it и представляет полностью рабочий пример создания алгоритма случайного леса на Python. Можете самостоятельно его запустить и попробовать поэкспериментировать, изменяя код (загрузка пакетов может занять некоторое время).
Заключение и выводы
Хотя мы действительно можем создавать мощные модели машинного обучения на Python, не понимая принципов их работы, знание основ позволит работать более эффективно. В этой статье мы не только построили и использовали на практике алгоритм случайного леса, но и разобрали, как работает эта модель.
Мы изучили работу дерева принятия решений, элемента, из которого состоит случайный лес, и увидели, как можно преодолеть высокую вариативность единичного дерева, комбинируя сотни таких деревьев в лес. Случайный лес работает на принципах случайной выборки образцов, случайного набора параметров и усреднения прогнозов.
В этой статье мы разобрали следующие ключевые концепции: