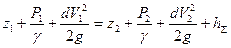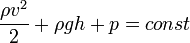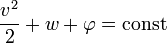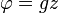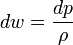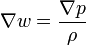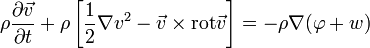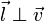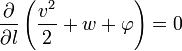Что отражает диаграмма бернулли

Диаграмма уравнения Бернулли

Диаграмма уравнения Бернулли является графическим представлением изменения различных слагаемых уравнения Бернулли по длине трубопровода. Диаграмма характеризует удельную механическую энергию потока и включает в себя три линии: линию полного напора, пьезометрическую линию и линию геометрического напора.

Линия полного напора характеризует полную удельную механическую энергию, то есть сумму кинетической и потенциальной энергий:

,

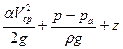
при этом удельная потенциальная энергия давления 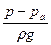при построении диаграммы определяется не абсолютным давлением, а избыточным.

Пьезометрическая линия характеризует удельную потенциальную энергию потока и представляет сумму двух слагаемых

.

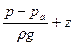
Геометрическая линия, или линия геометрического напора характеризует уклон трубопровода, т. е. изменение координаты z оси трубопровода.

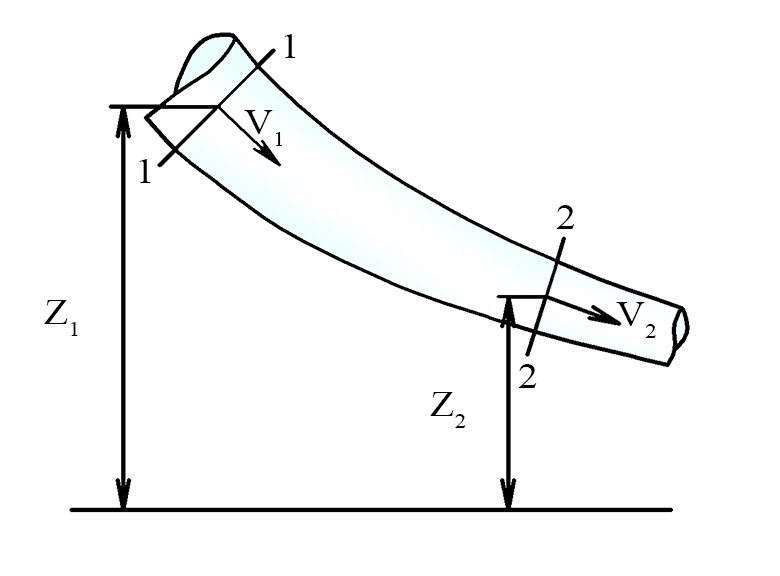
На рис.47 приведена диаграмма Бернулли для трубы переменного сечения. В первом сечении (1-1) полная удельная механическая энергия характеризуется величиной О₁А₁. По мере движения жидкости в трубе ее энергия расходуется, вследствие чего линия полного напора А₁А₂ всегда понижается. Если бы жидкость была невязкой, то полная удельная механическая энергия потока не менялась бы (линия А₁В) из-за отсутствия потерь. Расстояние между линиями полного напора А₁А₂ и пьезометрической С₁С₂ равно 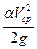и увеличивается по потоку, так как сечение трубы уменьшается, а это приводит к увеличению средней скорости и, следовательно, кинетической энергии. В сечении 2-2 полная удельная механическая энергия потока характеризуется величиной О₂А₂ и она меньше, чем полная энергия в сечении 1-1 на величину потерь h (А₂В).

Показанная на диаграмме Бернулли линия геометрических напоров D₁D₂ характеризует изменение удельной потенциальной энергии положения z, являясь, по существу осью трубопровода.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Диаграмма уравнения Бернулли

Диаграмма уравнения Бернулли представляет собой геометрическую интерпретацию, которая в графическом виде отображает изменения удельной энергии потока, то есть энергии, отнесенной к единице веса жидкости.

Диаграмма уравнения Бернулли состоит из пьезометрической линии P-P, отображающей изменение удельной потенциальной энергии и гидродинамической линии Е-Е, отображающей изменение удельной механической энергии.

Для двух любых контрольных сечений потока уравнение Бернулли записывается

Пьезометрическая линия расположена от плоскости сравнения 0-0 на расстоянии Z +P/γ;

Гидродинамическая линия расположена от плоскости0-0 на расстоянии Z+P/γ + £V 2 /2g

Величина Н= Z+ P/γ+ £V 2 /2g называется гидродинамическим напором.

Гидродинамическая линия имеет уклон вдоль потока, который называется гидродинамическим уклоном. Уклон пьезометрической линии, называется пьезометрическим уклоном.

Пьезометрическая и гидродинамическая линия на участках местных сопротивлений условно изображаются вертикальным уступом.

Высота уступа гидродинамической линии графически изображает местную потерю напора h_m, то есть ту часть энергии, которая вследствие местных сил трения обращается во внутреннюю, тепловую энергию и поэтому считается потерянной.

Источник

Диаграмма уравнения Бернулли

Диаграмма уравнения Бернулли является графическим представлением изменения различных слагаемых уравнения Бернулли по длине трубопровода. Диаграмма характеризует удельную механическую энергию потока и включает в себя три линии: линию полного напора, пьезометрическую линию и линию геометрического напора.

Линия полного напора характеризует полную удельную механическую энергию, то есть сумму кинетической и потенциальной энергий:

,при этом удельная потенциальная энергия давления при построении диаграммы определяется не абсолютным давлением, а избыточным.

Пьезометрическая линия характеризует удельную потенциальную энергию потока и представляет сумму двух слагаемых

.

Геометрическая линия, или линия геометрического напора характеризует уклон трубопровода, т. е. изменение координаты zоси трубопровода.

На рис.47 приведена диаграмма Бернулли для трубы переменного сечения. В первом сечении (1-1) полная удельная механическая энергия характеризуется величиной О₁А₁. По мере движения жидкости в трубе ее энергия расходуется, вследствие чего линия полного напора А₁А₂ всегда понижается. Если бы жидкость была невязкой, то полная удельная механическая энергия потока не менялась бы (линия А₁В) из-за отсутствия потерь. Расстояние между линиями полного напораА₁А₂ и пьезометрической С₁С₂ равно и увеличивается по потоку, так как сечение трубы уменьшается, а это приводит к увеличению средней скорости и, следовательно, кинетической энергии. В сечении 2-2 полная удельная механическая энергия потока характеризуется величиной О₂А₂ и она меньше, чем полная энергия в сечении 1-1 на величину потерь h (А₂В).

Показанная на диаграмме Бернулли линия геометрических напоров D₁D₂ характеризует изменение удельной потенциальной энергии положения z, являясь, по существу осью трубопровода.

Понятие гидравлического и пьезометрического уклона. В гидравлике различают гидравлический I и пьезометрический I_Pуклоны.

(2.22)

где — длина участка, для которого определяем гидравлический уклон;

— потери напора на участке потока длиной .

Если напорная линия криволинейная, гидравлический уклон будет различен в любой точке кривой. Например, гидравлический уклон в точке 1 напорной линии

(2.23)

И если пьезометрическая линия является криволинейной, то пьезометрический уклон в точке 1

При равномерном движении жидкости гидравлический и пьезометрический уклоны равны между собой, так как при равномерном движении живое сечение и средняя скорость потока постоянны и, следовательно, , тогда

Следует отметить, что пьезометрический уклон может быть или положительным, или отрицательным. Гидравлический уклон всегда будет положительным, так как напорная линия всегда понижается по направлению движения потока, поэтому обратного уклона не может быть.

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.008 сек.)

Источник

Уравнение Бернулли

Уравнение Бернулли для потока идеальной жидкости

Запишем для этого случая уравнение, связывающее между собой скорость движения жидкости и ее давление в каждом сечении.

Указанное уравнение называют законом или уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости.

Уравнение Бернулли можно записать и в другом виде, умножим обе части уравнения на g получим:

Физический смысл уравнения Бернулли

Составляющие уравнения Бернулли являются различными формами удельной (отнесенной к единице массы) механической энергии жидкости:

Физический и энергетический смысл уравнения Бернулли заключается в постоянстве полной удельной энергии вдоль элементарной струйки идеальной жидкости.

Уравнение Бернулли отражает закон сохранения механической энергии для идеальной несжимаемой жидкости.

Уравнение Бернулли для потока реальной вязкой жидкости

Если на участке между расчетными сечениями не совершается механическая работа, а движение является установившимся, без притока и отбора жидкости, и сама жидкость является несжимаемой, то для потока будут справедливы зависимости:

Иллюстрация уравнения Бернулли

Для иллюстрации закона Бернулли на координатной плоскости, совмещенной с принципиальной гидравлической схемой системы изображают напорную и пьезометрическую линии.

Уравнение Бернулли для горизонтальной трубы

Для горизонтальных трубопроводов и силовых гидроприоводов, в которых пьезометрический набор существенно превышает геометрический удобна следующая форма записи уравнения Бернулли:

Алгоритм решения задач с помощью уравнения Бернулли

Задачи с помощью уровнения Бернулли удобно решать в следующей последовательности:

Источник

Эффект Бернулли

Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

— плотность жидкости, — скорость потока, — высота, на которой находится рассматриваемый элемент жидкости, — давление, — ускорение силы тяжести.

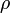
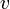
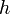
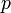
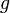
Константа в правой части обычно называется напором, или полным давлением, а также интегралом Бернулли. Размерность всех слагаемых — единица энергии, приходящейся на единицу объёма жидкости.

Это соотношение, выведенное Даниилом Бернулли в 1738 г., было названо в его честь уравнением Бернулли. (Не путать с дифференциальным уравнением Бернулли.)

Для горизонтальной трубы h = 0 и уравнение Бернулли принимает вид: .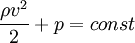

Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности ρ : .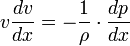

Согласно закону Бернулли полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

Полное давление состоит из весового ( ρgh ), статического (p) и динамического (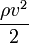) давлений.

Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров (например труба Вентури), водо- и пароструйных насосов.

Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю, то есть таких жидкостей, которые не прилипают к поверхности трубы. На самом деле экспериментально установлено, что скорость жидкости на поверхности твердого тела всегда в точности равна нулю.

Содержание

Одно из применений

Закон Бернулли можно применить к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда.

Согласно закону Бернулли приравняем полные давления на верхней поверхности жидкости и на выходе из отверстия:

,

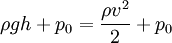
p₀ — атмосферное давление, h — высота столба жидкости в сосуде, v — скорость истечения жидкости.

Для сжимаемого идеального газа

— Адиабатическая постоянная газа p — давление газа в точке ρ — плотность газа в точке v — скорость течения газа g — ускорение свободного падения h — высота относительно начала координат

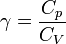
При движении в неоднородном поле gz заменяется на потенциал гравитационного поля.

Термодинамика закона Бернулли

Из статистической физики следует, что на линиях тока при адиабитическом течении остается постоянным следующее соотношение:

где w — энтальпия единицы массы, — потенциал силы.

— потенциал. Для силы тяжести

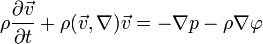
2. Запишем выражение для энтальпии и предположим, что энтропия системы постоянна (или, можно сказать, что течение адиабатично):

3. Воспользуемся следующими соотношениями из векторной алгебры:

— проекция градиента на некоторое направление равно производной по этому направлению.

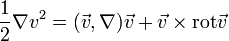
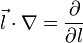
4. Уравнение Эйлера с использованием соотношений выведенных выше:

Спроецируем это уравнение на единичный вектор касательный к линии тока, учитывая следующее:

— условие стационарности — так как

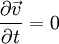
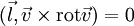
То есть на линиях тока в стационарной адиабатической жидкости выполняется следующее соотношение:

Приложение

См. также

Литература

Примечания

Полезное

Смотреть что такое «Эффект Бернулли» в других словарях:

Эффект Магнуса — при воздействии на вращающийся шар Эффект Магнуса физическое явление, возникающее при обтекании вращающегося тела потоком жидкости или газа. Образуется сила … Википедия

Эффект Вентури — … Википедия

Магнуса эффект — Эффект Магнуса при воздействии на вращающийся шар Эффект Магнуса физическое явление, возникающее при обтекании вращающегося тела потоком жидкости или газа. Образуется сила, воздействующая на тело и направленная перпендикулярно направлению потока … Википедия

Закон Бернулли — является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости: Здесь плотность жидкости, скорость потока, высота, на которой находится рассматриваемый… … Википедия

СТЕНОЗ СУБАОРТАЛЬНЫЙ ГИПЕРТРОФИЧЕСКИЙ — мед. Гипертрофический субаортальный стеноз редкая форма наследственной гипертрофической кардиомиопатии, в основном затрагивающей межжелудочковую перегородку (см. Приложение 2. Наследственные болезни: картированные фенотипы). Последняя вместе с… … Справочник по болезням

СССР. Естественные науки — Математика Научные исследования в области математики начали проводиться в России с 18 в., когда членами Петербургской АН стали Л. Эйлер, Д. Бернулли и другие западноевропейские учёные. По замыслу Петра I академики иностранцы… … Большая советская энциклопедия

Теория гравитации Лесажа — Необходимо проверить качество перевода и привести статью в соответствие со стилистическими правилами Википедии. Вы можете помочь … Википедия

Гравитация Фатио-Леcажа — В Викитеке есть оригинал текста по этой теме. См. The Le Sage Theory of Gravitation В 1690 году швейцарский математик[1] Николас Фатио де Дуилье и в 1756 Жорж Луи Ле Саж в Женеве предложили простую кинетическую теорию гравитации, которая дала… … Википедия

Гравитация Фатио-Лесажа — В Викитеке есть оригинал текста по этой теме. См. The Le Sage Theory of Gravitation В 1690 году швейцарский математик[1] Николас Фатио де Дуилье и в 1756 Жорж Луи Ле Саж в Женеве предложили простую кинетическую теорию гравитации, которая дала… … Википедия

Важнейшие открытия в физике — История технологий По периодам и регионам: Неолитическая революция Древние технологии Египта Наука и технологии древней Индии Наука и технологии древнего Китая Технологии Древней Греции Технологии Древнего Рима Технологии исламского мира… … Википедия

Источник