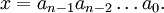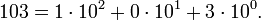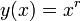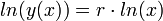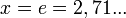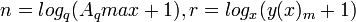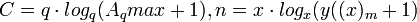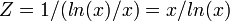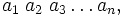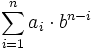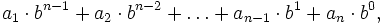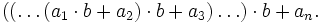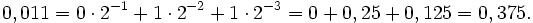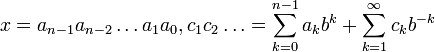Что относится к позиционной системе счисления

Позиционные системы счисления

Позиционной называют систему счисления, в которой положение (позиция) цифры определяет вес числа. Основные виды позиционных систем:

Немного истории

Первыми в истории человечества позиционную систему счисления применяли индейцы майя примерно 500 лет до нашей эры. Она использовалась для составления календарей и имела в основании число 20.

Современная позиционная система счисления уходит корнями в Индию, в V век нашей эры. И несмотря на то, что в ней используются арабские цифры, именно индусы стали ее основоположниками. А за счет удобных форм записи и выполнения арифметических действий, создание позиционной системы дало мощный толчок развитию математики.

Основание и алфавит

Например, с помощью трех цифр 0, 1 и 2 можно составить троичную систему счисления. Все правила построения чисел будут при этом соответствовать другим позиционным системам: двоичной, десятичной и так далее. А ее основание будет равно трем:

Разряд числа

Разряд — это место, позиция цифры в записи числа. Например, в 125: цифра 5 относится к разряду единиц, 2 — к разряду десятков, 5 — к разряду сотен. Данное число можно также представить в виде суммы 100 + 20 + 5 и выделить основание системы в каждом слагаемом в той или иной степени:

125₁₀ = 1 ∙ 100 + 2 ∙ 10 + 5 ∙ 1 = 1 ∙ 10 2 + 2 ∙ 10 1 + 5 ∙ 10 0

Если обратить внимание на показатели степени, то наблюдается закономерность — соответствие порядковому номеру цифры слева направо, начиная с нуля:

Развернутая форма записи числа

Данный способ записи числа действует и для любой другой позиционной системы счисления и называется развернутой формой:

где A — число, q — основание системы счисления, а n — количество разрядов числа. При этом свернутой формой будет запись вида:

Например, развернутая форма числа 753 в восьмеричной системе счисления будет иметь следующий вид:

753₈ = 7 ∙ 8 2 + 5 ∙ 8 1 + 3 ∙ 8 0

Представление дробей

Если же необходимо представить в развернутой форме дробь, то формула будет следующей:

где A — число, q — основание системы счисления, n — количество целых разрядов, а m — количество дробных разрядов числа. Свернутой формой, соответственно, является запись вида:

Например, для 1001,101 в двоичной системе счисления развернутая форма будет выглядеть так:

Плюсы и минусы позиционных систем

Главным удобством позиционной системы счисления является то, что запись больших чисел имеет краткую и удобную форму. Это также стало причиной их использования в программировании: большие числа занимают в данной форме меньшее количество памяти ЭВМ.

Источник

Определение позиционной и непозиционной системы счисления

Системы счисления

Система счисления — метод записи чисел с помощью письменных знаков.

Системы делятся на позиционные, непозиционные и смешанные. Смысл их в том, чтобы дать каждому числу уникальное представление. В разных системах одно и то же число может быть записано по-разному. Символы, используемые для записи чисел, называют цифрами, даже когда система использует в дополнение к арабским цифрам или вместо них буквы латинского алфавита.

Что такое позиционная система

Позиционная система счисления — система счисления, в которой значение каждого числового знака в записи числа зависит от его позиции.

В позиционной системе количественный эквивалент каждой цифры зависит от места ее записи в коде числа. Любое целое число x в d-ичной позиционной системе счисления является конечной линейной комбинацией степеней числа d:

k — показатель разряда.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В общем случае представить произвольное число x в системе счисления с заданным основанием d означает расписать его по формуле:

Таким образом, в любой позиционной системе число может быть представлено в виде многочлена.

Что такое непозиционная система

Непозиционная система — это такая система счисления, в которой положения цифры в записи числа не зависит величина, которую она обозначает.

В непозиционных системах счисления величина, которую обозначает цифра, не зависит от ее места в коде числа.

Еще до нашей эры разные народы независимо друг от друга отказывались от унарной системы счисления, в которой количество предметов обозначали таким же количеством одинаковых значков, и переходили к более удобным системам. Например, у египтян система счисления была десятичной, но запись числа составлялась только из иероглифов 1, 10, 100, 1000. Их нужно было складывать, поэтому не имело значения, в каком порядке они записаны.

Отличие между системами

Чтобы пользоваться позиционной системой счисления, достаточно знать, как в ней изображаются цифры и что они обозначают, а также ее основание — количество уникальных цифр. Порядок записи во всех позиционных системах одинаков.

В непозиционных системах количество цифр-символов может достигать десятков и даже сотен, так как для записи больших чисел постоянно приходится вводить новые символы. Для чтения числа нужно знать правила его записи. Часто приходится выполнять арифметические операции, например, вычитание и сложение.

Достоинства позиционной системы

Простое выполнение подсчета

У всех позиционных систем одни и те же алгоритмы выполнения арифметических действий. Также в позиционных системах удобно работать с дробями и отрицательными числами, которые зачастую просто невозможно представить в непозиционных системах.

Главные свойства позиционных систем:

Малое количество символов в записи

Позиционные системы используют только десять арабских цифр. Системы с основанием больше десяти добавляют к цифрам 26 латинских букв. В некоторых системах используют круглые и квадратные скобки.

Чем больше основание системы счисления, тем меньшее количество цифр понадобится для записи числа. Числа, состоящие из трех разрядов в десятичной системе, могут иметь всего два разряда в шестнадцатеричной.

Основание позиционной системы

Обычно за основание принимают целое натуральное число. Но существуют также системы с дробным или отрицательным основанием. Последние называют нега-позиционными.

Основание позиционной системы счисления — это количество уникальных символов, изображающих ее цифры.

Таким образом, чтобы найти эту главную характеристику любой позиционной системы, достаточно подсчитать количество цифр в ней.

Классификация позиционных систем

Двоичные

Двоичная система — система счисления, в которой в качестве базовых чисел выбираются степени числа два.

Чтобы не путать их с числами, записанными в десятичной системе счисления, справа внизу указывают основание системы счисления. Обычно число при этом заключают в скобки.

Двоичную систему использовали задолго до возникновения информационных технологий. Во втором тысячелетии до нашей эры народы Южной Америки кодировали двоичной системой свои записи, в том числе и не числовые. Узелок и ровный участок нити чередовались друг с другом.

В современной двоичной системе, на основе которой был создан телеграф, а позже — реле и переключатели, единица обозначает наличие сигнала, ноль — его отсутствие. Цифровые электронные схемы работают по тому же принципу. Также на нем основаны сигнальные системы, использующиеся до сих пор, например, азбука Морзе.

Восьмеричные

Когда-то два индейских племени решили, что им удобно при счете смотреть на восемь промежутков между пальцами, а не на сами пальцы. Восьмеричная система счисления отразилась в их языках, в которых только восемь слов, обозначающих цифры.
В двадцатом веке, когда для написания программ требовалось зашифровывать все больше информации в двоичной системе и упростить вычисления для людей, придумали альтернативную систему, которая позволила сократить количество цифр в коде. Число восемь — это два в кубе, поэтому перевести записи из двоичной системы в восьмеричную и обратно проще, чем в десятичную.

Десятичные

Элементы числовой базы, или ключевые числа, в десятичной системе счисления представляют собой степени десяти: 10 = 10^1, 100 = 10^2, 1000 = 10^3.
В системе всего десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число 10 — основание системы счисления. Цифры от 0 до 9 представляют собой коэффициенты разложения числа по степеням десяти.

Родиной десятичной системы счисления считается Индия, хотя еще в вавилонской цивилизации с ее шестидесятеричной системой использовались закодированные десятичные цифры, а инки в своей узелковой письменности кодировали информацию десятью цветами. Но именно в Индии начали строго соблюдать порядок разрядов числа при записи и ставить ноль, чтобы избежать путаницы. Примерно в середине VIII века эту систему стали использовать другие страны. В Европе она распространилась к XVI веку и была названа «арабской».

Шестнадцатеричные

Шестнадцатеричные системы, как и восьмеричные, появились для упрощения взаимодействия с компьютером. Кроме арабских цифр, в них используются еще и латинские буквы от А до F. В разных языках программирования для записи чисел в шестнадцатеричной системе разные правила, называемые синтаксисом.

Пятеричная

Система, связанная с количеством пальцев на одной руке, использовалась в Китае и у некоторых племен Африки. В китайском языке у иероглифов, обозначающих цифры от шести до девяти, был один и тот же знак в начале — сокращенное обозначение цифры пять. Для записи чисел в этой системе используются цифры 0, 1, 2, 3, 4.

Двенадцатеричная

Если большим пальцем руки сосчитать число фаланг на других пальцах этой руки, получится двенадцать. Группы по двенадцать предметов называли во многих европейских языках словами, схожими с русским словом «дюжина»: duodezim на латыни, douzaine на французском, dozzina на итальянском, dozen на английском. Римляне пользовались двенадцатеричными дробями, \frac1 <12>они называли унцией.

В Европе счет дюжинами долгое время, вплоть до XVIII века, сохранялся наравне с десятеричной системой. Дюжина дюжин составляла гросс (от немецкого слова «большой»), дюжина гроссов — массу. Признаки влияния числа 12 заметны в англо-американской системе линейных мер, в которой 1 фут равен 12 дюймам, 1 дюйм — 12 линиям, 1 линия — 6 точкам.

Шестидесятеричная

Первой позиционной системой счисления считается шестидесятеричная система в Древнем Вавилоне. Ее основание до сих пор применяют для измерения времени. Система счисления времени — смешанная, но для перевода минут в секунды или часы потребуется именно шестидесятеричная система.

Для измерения углов и записи координат (широты, долготы) тоже используют эту систему, так как изначально астрономические координаты записывали в шестидесятеричных дробях. По аналогии с часом градус делят на шестьдесят минут, минуту — на шестьдесят секунд.

Двадцатеричная

Двадцатеричную систему называют вигезимальной. Эта система, как и десятеричная, связана с количеством пальцев, поэтому многие народы изобрели ее независимо друг от друга. Основание 20 сохранилось в лингвистической структуре их языков, именно на нем основана система счета в разговорной речи. Например, во французском языке «восемьдесят» состоит из слов «четыре» и «двадцать».

Римская система счисления

Описание

Римская система счисления относится к непозиционным. Она известна всему миру и широко применяется до сих пор. Это связано не с какими-то особыми достоинствами, а скорее с политическим и культурным влиянием Древнего Рима на европейскую цивилизацию.
Сейчас римская система используется в русском языке для обозначения:

В других странах свои особенности употребления римских цифр: в Европе ими часто записывают номер года, в Латвии — день недели.
Считается, что в основу римских цифр легли жесты:

100 и 1000 обозначаются буквами C и М — первыми буквами соответствующих латинских слов.

Основные характеристики

Для записи чисел используют семь букв латинского алфавита:

Сначала записываются тысячи, потом сотни, потом десятки и единицы. Ноль в системе отсутствует, но раньше вместо него использовали букву N. От позиционных систем римская отличается использованием принципов сложения и вычитания. Когда большая цифра стоит перед меньшей, они складываются. Когда меньшая стоит перед большей — вычитаются.

Источник

Позиционная система

Позиционная систе́ма счисле́ния — система счисления, в которой один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у мусульман.

Содержание

Определение

Целое число x в b-ричной системе счисления представляется в виде конечной линейной комбинации степеней числа b:

, где a_k — это целые числа, называемые цифрами, удовлетворяющие неравенству .

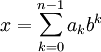
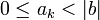
Если не возникает разночтений (например, когда все цифры представляются в виде уникальных письменных знаков), число x записывают в виде последовательности его b-ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо:

Например, число сто три представляется в десятичной системе счисления в виде:

Примеры позиционных систем счисления

Запись чисел

Для записи чисел системы счисления с основанием до 36 включительно в качестве цифр (знаков) используются арабские цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и затем буквы латинского алфавита (a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z). При этом, a = 10, b = 11 и т. д., иногда x = 10.

При одновременной работе с несколькими системами счисления для их различения основание системы обычно указывается в виде нижнего индекса, который записывается в десятичной системе:

123₁₀ — это число 123 в десятичной системе счисления; 1111011₂ — то же число, но в двоичной системе.

В некоторых специальных областях применяются особые правила указания основания. Например, в программировании шестнадцатеричная система обозначается:

В некоторых диалектах языка Си по аналогии с «0x» используется префикс «0b» для обозначения двоичных чисел. (Обозначение «0b» не входит в стандарт ANSI C.)

Плотность записи чисел

1. Описание по С.В.Фомину (подобное же описание приводится в работе А.Кушнерова [1] со ссылкой на малоизвестную теорему Джона фон Неймана 1946 г. «о компактности систем счисления», но в этой работе на рис.1 приводится график для фиксированного числа знаков .)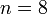

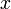
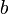
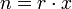
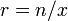
— основание системы счисления (число знаков (цифр) в одном разряде, число устойчивых состояний триггера) ()

— число знаков (число элементов, число инверторов в одном триггере) (в трёхразрядном (трёхпозиционном) десятичном числе 30 знаков) (экономичность системы)

— число разрядов (число позиций, длина разрядной сетки, число разрядов регистра, число триггеров в регистре)

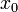
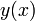
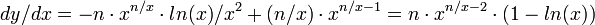
Необходимое условие того, что в данной точке функция достигает максимума, состоит в обращении в нуль её производной в этой точке. В данном случае производная этой функции равна .

Приравняв её нулю, получим, что 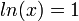, т.е. .

Так как слева от точки производная положительна, а справа отрицательна, то, в силу известных теорем дифференциального исчисления, в этой точке наша функция действительно имеет максимум.

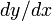
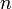
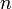
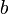
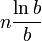
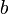
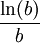
При условии равновероятности появления каждой из цифр в записи числа информационная энтропия записи -значного (в данном случае автор употребил слово -значного в смысле -разрядного, -позиционного) числа в системе счисления с основанием принимает значение (с точностью до постоянного коэффициента). Поэтому плотность записи (то есть количество информации на одну позицию) чисел в системе счисления с основанием равна .

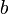
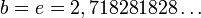
Плотность записи, как функция от , принимает максимальное значение в точке при .

Таким образом, наибольшей плотностью записи чисел (информации) обладает система счисления с нецелочисленным основанием . Из систем счисления с целочисленными основаниями наибольшей плотностью записи чисел (информации) обладает троичная система счисления. Двоичная и четверичная системы счисления делят второе место. Остальные целочисленные системы счисления имеют меньшую плотность записи чисел (информации).

— основание системы счисления (число знаков (цифр) в одном разряде, число устойчивых состояний триггера) ()

— число разрядов (число позиций, длина разрядной сетки, число разрядов регистра, число триггеров в регистре)

— число знаков (число элементов, число инверторов в одном триггере) (в трёхразрядном (трёхпозиционном) десятичном числе 30 знаков) (экономичность системы)

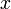
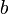
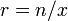
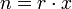
Число записывыемых (представимых, представляемых) чисел (кодов)

Натуральный логарифм числа представимых чисел (кодов)

Удельная натуральнологарифмическая плотность записи чисел 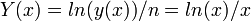[натуральный логарифм числа представимых чисел/число знаков (элементов)] наибольшая в точке экстремума, в которой первая производная равна нулю.

Первая производная от натуральнологарифмической плотности записи чисел 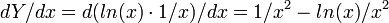равна нулю в точке

Число знаков на запись чисел (аппаратные затраты)

1. По О.А.Акулову и Н.В.Медведеву (приведены обозначения по первоисточнику и общие обозначения):

— основание системы счисления (число знаков (цифр) в одном разряде, число устойчивых состояний триггера)

— число разрядов (число позиций, длина разрядной сетки, число разрядов регистра, число триггеров в регистре)

— число элементов (экономичность системы) (число знаков, число инверторов в одном триггере)

— число представляемых (записываемых, представимых) чисел

— наибольшее представляемое (записываемое, представимое) число

— относительные аппаратные затраты (экономичность системы счисления) по Акулову и Медведеву

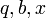
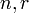
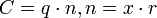
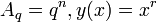
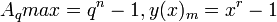
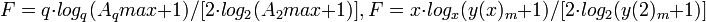
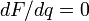
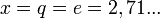
Минимальные относительные аппаратные затраты будут при при . [3]

2. Более простое описание:

Аппаратные затраты являются функцией обратной функции натуральнологарифмической плотности записи чисел, поэтому, поделив 1 на функцию натуральнологарифмической плотности записи чисел получим более простое выражение функции натуральнологарифмических аппаратных затрат:

Свойства

Позиционная система счисления обладает рядом свойств:

Переход к другому основанию

Перевод произвольной позиционной системы счисления в десятичную

Если число в b-ричной системе счисления равно

то для перевода в десятичную систему вычисляем такую сумму:

или, в более наглядном виде:

либо, наконец, в виде схемы Горнера:

101100₂ = = 1 · 2 5 + 0 · 2 4 + 1 · 2³ + 1 · 2² + 0 · 2 1 + 0 · 1 = = 1 · 32 + 0 · 16 + 1 · 8 + 1 · 4 + 0 · 2 + 0 · 1 = = 32 + 8 + 4 + 0 = 44₁₀

Перевод из десятичной в произвольную позиционную систему счисления

Для перевода необходимо делить число с остатком на основание счисления до тех пор, пока частное больше основания счисления.

Перевод из двоичной в восьмеричную и шестнадцатеричную системы

Для этого типа операций существует упрощенный алгоритм.

Для восьмеричной — разбиваем число на триплеты, преобразуем триплеты по таблице

Для шестнадцатеричной — разбиваем на квартеты, преобразуем по таблице

Перевод из восьмеричной и шестнадцатеричной систем в двоичную

Для этого типа операций существует упрощенный алгоритм-перевёртыш.

Для восьмеричной — преобразуем по таблице в триплеты

Для шестнадцатеричной — преобразуем по таблице в квартеты

Перевод из произвольной системы счисления в десятичную

Рассмотрим пример перевода двоичного числа 1100,011₂ в десятичное. Целая часть этого числа равна 12 (см. выше), а вот перевод дробной части рассмотрим подробнее:

Точно также осуществляется перевод из любой системы счисления, только вместо «2» ставится основание системы.

Для удобства перевода, целую и дробную части числа переводят отдельно, а результат потом суммируют.

Перевод из двоичной системы в 8- и 16-ричную

Перевод дробной части из двоичной системы счисления в системы счисления с основаниями 8 и 16 осуществляется точно также, как и для целых частей числа, за тем лишь исключением, что разбивка на октавы и тетрады идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа. Например, рассмотренное выше число 1100,011₂ будет выглядеть как 14,3₈ или C,6₁₆.

Перевод из десятичной системы в произвольную

Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в нуль и начать умножение получившегося числа на основание той системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в нуль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль. Ниже приводится пример перевода числа 103,625₁₀ в двоичную систему счисления.

Точно также осуществляется перевод в системы счисления с любым основанием.

Сразу нужно отметить, что этот пример специально подобран, в общем случае очень редко удаётся завершить перевод дробной части числа из десятичной системы в другие системы счисления, а потому, в подавляющем большинстве случаев, перевод можно осуществить с какой либо долей погрешности. Чем больше знаков после запятой — тем точнее приближение результата перевода к истине. В этих словах легко убедиться, если попытаться, например, перевести в двоичный код число 0,626.

Вариации и обобщения

Запись рациональных чисел

Рациональное число x в b-ричной системе счисления представляется в виде линейной комбинации (вообще говоря, бесконечной) степеней числа b:

где a_k — цифры целой части (до запятой), c_k — цифры дробной части (после запятой), n — число разрядов целой части.

Конечной записью в b-ричной системе счисления обладают только рациональные числа, представимые в виде 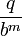, где m и q — целые числа; рациональные числа, не представимые в таком виде, записываются в виде периодических дробей.

Симметричные позиционные системы счисления

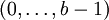
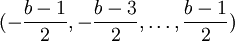
Такие системы счисления отличаются от обычных тем, что используют цифры не из множества , а из множества . Чтобы цифры были целыми, нужно, чтобы b было нечётным. В симметричных системах счисления не требуется дополнительных обозначений для знака числа. Кроме того, вычисления в симметричных системах удобны тем, что не требуется особых правил округления — оно сводится к простому отбрасыванию лишних разрядов, что резко уменьшает систематические ошибки вычислений.

Чаще всего используется симметричная троичная система счисления с цифрами (-1,0,1). Она применяется в троичной логике и была технически реализована в вычислительной машине «Сетунь».

Отрицательные основания

Существуют позиционные системы с отрицательными основаниями, называемые нега-позиционными:

Нецелочисленные основания

Иногда также рассматривают позиционные системы с нецелочисленными основаниями:

Примечания

Ссылки

Полезное

Смотреть что такое «Позиционная система» в других словарях:

ПОЗИЦИОННАЯ СИСТЕМА — система счисления, основана на принципе позиционного, или поместного, значения цифр, т. е. на том, что одна и та же цифра получает различные числовые значения в зависимости от ее места в записи чисел. К позиционным системам принадлежит… … Большой Энциклопедический словарь

позиционная система — система счисления, основанная на принципе позиционного, или поместного, значения цифр, то есть на том, что одна и та же цифра получает различные числовые значения в зависимости от её места в записи чисел. К позиционной системе принадлежит… … Энциклопедический словарь

Позиционная система — система счисления (См. Счисление), основанная на принципе позиционного, или поместного, значения цифр, т. е. на том, что одна и та же цифра получает различные числовые значения, в зависимости от её места в записи чисел. К П. с.… … Большая советская энциклопедия

ПОЗИЦИОННАЯ СИСТЕМА — система счисления, осн. на принципе позиционного, или поместного, значения цифр, т. е. на том, что одна и та же цифра получает разл. числовые значения в зависимости от её места в записи чисел. К П с. принадлежит общепринятая ныне десятичная… … Естествознание. Энциклопедический словарь

Позиционная система счисления — система счисления, использующая для записи чисел ограниченное число знаков, интерпретация которых зависит от места в записи числа. См. также: Позиционные системы счисления Системы счисления Финансовый словарь Финам … Финансовый словарь

позиционная система счисления — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN positional system … Справочник технического переводчика

Позиционная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия

Позиционная система счисления с основанием 64 — Base64 буквально означает позиционная система счисления с основанием 64. Здесь 64 это наибольшая степень двойки (26), которая может быть представлена с использованием печатных символов электронной почте для представления бинарных файлов в… … Википедия

Нега-позиционная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия

Источник