Что относится к основным факторам которые учитываются при оценке устойчивости бортов

10.04.202224.04.2022 admin 0 Comments

Устойчивость бортов карьера. Факторы, влияющие на устойчивость бортов.

С увеличением глубины карьера устойчивость бортов карьера приобретает важное значение. С увеличением глубины карьера увеличивается опасность обрушения бортов карьера при неправильном определении углов погашения. С другой стороны нерациональное уменьшение углов бортов карьера вызывает необходимость в дополнительных горных работах по разносу бортов карьера. Таким образом при определении устойчивости бортов карьера приходится учитывать действие двух ограничивающих противоречивых факторов: 1) создание безопасных условий работы, вызывающих выполаживаение бортов карьера; 2) стремление к уменьшению объёмов работ по дополнительному разносу бортов карьера, вызывающее увеличение угла откоса борта. Основные факторы влияющие на устойчивость бортов карьера:

1. Физико-механические свойства пород слагающие борта карьера;

2. Наличие и характер поверхностей ослабления в пределах борта карьера;

3. Размеры и форма карьера;

4. Обводнённость участков разработки;

5. Время существования карьера;

6. Характер буровзрывных работ в карьере;

7. Наличие нагрузок от сооружений на бортах карьера;

Физико-механические свойства горных пород являются одним из наиболее важных факторов устойчивости бортов, т.к. они определяют напряжённое состояние в бортах карьера под действием внутренних и внешних нагрузок из которых наибольшее значение имеет – главное касательное напряжение.

Наиболее важными свойствами пород влияющих на устойчивость являются плотность, пористость, трещиноватость.

Размеры и форма карьерного поля оказывают влияние на устойчивость бортов. Особенно сильно влияет глубина карьера. С её увеличением резко возрастает усилие сдвигающее породы в сторону выработанного пространства. Форма карьера в плане так же оказывает влияние.

Наличие и характер расположение бортов карьера по отношению к поверхностям ослабления. К поверхностям ослабления относятся: контакты различных слоёв горных пород, тонкие прослойки, особенно отличающиеся от окружающих пород физико-механическими свойствами, сильно обводнённые тонкие слои, трещины в массиве горных пород, слоистость в пределах массива прилегающих к борту, тектонические нарушения и другие нарушения сплошности массива.

47.Виды нарушений устойчивости бортов карьера. Мероприятия по повышению устойчивости бортов карьера.

Выделяют два вида нарушений устойчивости борта карьера: оползни и обвалы. Оползни – это такое нарушение устойчивости откоса борта, которое характеризуется медленным отделением части массива с постепенным перемещением в сторону выработанного пространства по поверхности ослабления без заметной деформации её в первый период оползания. Обвал – это такое нарушение устойчивости борта при котором часть массива внезапно отделяется и быстро перемещается в сторону выработанного пространства, опрокидывается и разрушается на части.

Проводятся следующие мероприятия:

— осушение примыкающих к борту пород;

— не подрабатывать пласты пород падающих в сторону выработанного пространства, а в случае необходимости подработки выполаживать борт до поверхности ослабления;

— строго производить заоткоску уступов до значений предусмотренных проектом;

— не размещать на бортах, склонных к оползанию, отвалов и тяжёлых сооружений;

— избегать массовых взрывов при подходе к проектному контуру карьера;

— строго выдерживать установленные нормами параметры элементов борта карьера и уступа;

— для предотвращения оползания бортов при необходимости оставлять подпорные целики;

— по возможности в местах склонных к оползанию устраивать вогнутые борта карьера;

48.Определение рабочих и нерабочих углов откосов бортов карьера

Углы откоса бортов карьера определяются проведением расчётов по двум направлениям. С одной стороны борт отстраивается по чисто геометрическим правилам с учётом факторов, которые можно учесть;

А с другой стороны после предварительного построения контуров борта карьера производится его расчёт оп условиям устойчивости горных пород в пределах борта карьера. В этом случае расчёты ведутся по методике принятой в механике грунтов.

Если правильно выбрать параметры обеспечивающие устойчивость нерабочих уступов карьера (альфа_н, Н_у). Число и параметры предохранительных и транспортных берм на нерабочих бортах карьера с учётом правил безопасности ведения горных работ и технологии ведения горных работ, то конструкция нерабочего борта карьера не представляет особой сложности.

Исследование по величине устойчивых углов откосов нерабочих бортов карьеров указывает на то, что чаще всего величина углов откосов полученных по условиям принятой схемы вскрытия, системой разработки, величины и количества предохранительных и транспортных берм, оказываются меньше чем получены по расчётам из условия устойчивости бортов.

49.Управление состоянием массива горных пород. Основные методики.

Под управлением состоянием массива горных пород пониматься комплекс научных и технических мероприятий направленных на достижение оптимальных параметров карьерных откосов, при которых, обеспечивается безопасность ведения горных работ и их максимальная экономическая эффективность. Комплекс этих мероприятий определяется природными и горнотехническими условиями при разработке месторождения.

Комплексная методика технологического управления в бортах карьера включает методики:

— выбора оптимального направления развития горных работ с учётом условий устойчивости бортов карьера;

— управление в состоянии бортах путём изменения их конструктивных параметров;

— постановки бортов в предельное положение.

Основой специальной технологии управления состоянием пород в бортах карьера является искусственное укрепление неустойчивых участков и упрочнения горных пород.

Основные понятия о фронте горных работ карьера.

Направление развития горных работ на уступе выбирается непроизвольно. Месторасположение разрезной траншеи должно соответствовать проектному плану горных работ с тем, что бы обеспечивалась необходимое число вскрышных и добычных забоев в эксплутационный период разработки слоя, планомерность вскрышных и добычных работ. Фронт работ уступа различают прежде всего по следующим признакам:

1.Фронт работ расположен вдоль длиной оси карьерного поля

2. Фронт работ расположен вдоль короткой оси карьерного поля

3. Фронт работ расположен концентрически или по эллипсу

1.Однородный фронт работ, если он сложен только вскрышными породами или полезным ископаемы одного сорта. Ведётся валовая выемка горной массы.

2. Разнородный фронт работ: чередуются блоки пустых пород, полезного ископаемого и его различных сортов. Выемка в забоях раздельная, деление на блоки

3. Сложно-разнородный фронт работ, когда в его пределах практически не возможно выделить блоки только с пустыми породами или только с полезным ископаемым одного сорта. Ведут валовую выемку породу.

III)По направлению перемещения горной массы:

1.Фронт работ с поперечным перемещением горной массы, при складировании вскрышных пород в выработанном пространстве.

2. Фронт работ с продольным перемещением горной массы из забоев с применением карьерного транспорта.

IV) По погрузке горной массы:

1. Нижняя погрузка горной массы

2. Верхняя погрузка горной массы

3. Верхняя экскаваторная перевалка горной массы

4. Нижняя экскаваторная перевалка горной массы

V) По числу транспортных грузовых выходов:

1. Одинарный фронт (один грузовой транспортный выход с уступа)

2. Сдвоенный фронт (два грузовых выхода с уступа)

VI) По движению транспорта:

1) Тупиковый фронт: с возвратным движением транспортных средств.

2) Сквозной: с поточным движением транспорта.

VII) По положению транспортного выхода:

2) Центральный фронт.

51.Направления перемещения фронта горных работ в пределах карьерного поля.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник

Что относится к основным факторам которые учитываются при оценке устойчивости бортов

ФЕДЕРАЛЬНАЯ СЛУЖБА ПО ЭКОЛОГИЧЕСКОМУ, ТЕХНОЛОГИЧЕСКОМУ И АТОМНОМУ НАДЗОРУ

от 13 ноября 2020 года N 439

2. Настоящий приказ вступает в силу с 1 января 2021 г. и действует до 1 января 2027 г.

в Министерстве юстиции

18 декабря 2020 года,

регистрационный N 61603

УТВЕРЖДЕН
приказом Федеральной службы
по экологическому, технологическому
и атомному надзору
от 13 ноября 2020 года N 439

Федеральные нормы и правила в области промышленной безопасности «Правила обеспечения устойчивости бортов и уступов карьеров, разрезов и откосов отвалов»

I. Область применения

3. Требования Правил являются обязательными для юридических лиц (индивидуальных предпринимателей), осуществляющих ведение горных работ и (или) разработку месторождений полезных ископаемых открытым способом, а также проектирование, ввод в эксплуатацию, консервацию и ликвидацию карьеров, разрезов и отвалов.

В случае если на предшествующих проектированию новой стадии освоения месторождения был выполнен весь требуемый комплекс исследований (определяется проектной организацией), дополнительных инженерно-геологических исследований не проводится.

5. Организация, эксплуатирующая объект ведения открытых горных работ, должна обеспечить:

контроль за соблюдением проектных параметров бортов и уступов карьера, разреза и откосов отвала;

проведение визуальных и инструментальных наблюдений за состоянием бортов, уступов и откосов;

выявление зон и участков возможного проявления разрушающих деформаций бортов, бортов, уступов и откосов и организацию на этих участках стационарных инструментальных наблюдений и (или) дистанционного мониторинга;

изучение выявленных нарушений устойчивости бортов, уступов, откосов, документирование нарушений, установление характера нарушений, степени опасности и причин возникновения;

изучение геологических, инженерно-геологических, гидрогеологических условий месторождения, структуры и условий залегания породных слоев, массива горных пород и пород основания отвалов;

разработку и выполнение (проведение) противодеформационных мероприятий, в том числе укрепление ослабленных зон и участков, либо изменение профиля уступов на этих участках, либо обеспечение запрета доступа в опасную зону при условии, что в ней не ведутся горные работы;

контроль за состоянием противодеформационных сооружений и выполнением мероприятий, предотвращающих нарушение устойчивости бортов, уступов, откосов;

сохранность объектов, расположенных на земной поверхности в границах горных отводов и на прилегающих к ним территориях;

ликвидацию (рекультивацию) объекта ведения открытых горных работ, после завершения горных работ.

6. В случае выявления в процессе эксплуатации, технического перевооружения, ликвидации (консервации) карьера, разреза, отвала отклонений от значений физико-механических характеристик и (или) структуры массива горных пород, принятых при оценке устойчивости уступов, бортов, откосов при проектировании, эксплуатирующей организацией должен проводиться перерасчёт параметров бортов и уступов или откосов отвала, с учётом вновь полученных исходных данных. Для выполнения работ по перерасчету параметров горнотехнических конструкций на основании решения технического руководителя эксплуатирующей организации могут привлекаться проектные и (или) научные организации.

7. Для обоснования параметров бортов, уступов, откосов при осуществлении технического перевооружения, в процессе эксплуатации, ликвидации (консервации) объекта ведения открытых горных работ должны учитываться результаты инженерно-геологического, гидрогеологического изучения массива и мониторинга устойчивости на предыдущих этапах отработки месторождения и работ по отвалообразованию. В случаях, когда фактические параметры устойчивости бортов, уступов и откосов не соответствуют проектным и превышают допустимые отклонения, а также допустимые значения деформаций бортов, уступов, откосов, горных выработок и объектов в проектную документацию вносятся соответствующие изменения (дополнения).

8. Эксплуатирующей организацией должен выполняться прогноз устойчивости бортов и уступов карьеров, разрезов и откосов отвалов, результаты которого являются основой разработки противодеформационных мероприятий, включаемых в план развития горных работ на предстоящий календарный год.

9. Прогноз устойчивости бортов и уступов карьеров, разрезов и откосов отвалов является обязательным для объектов ведения открытых горных работ II класса опасности и (или) при комбинированной разработке месторождения.

В случаях, когда отклонения от проектных параметров и деформаций бортов и уступов карьеров, разрезов и откосов отвалов не нарушают требований безопасности, прогноз устойчивости допускается не производить.

II. Факторы, влияющие на устойчивость бортов, уступов карьеров, разрезов и откосов отвалов

10. Факторы в зависимости от горно-геологических условий пользования недрами определяются проектной документацией на пользование участком недр и могут уточняться в процессе эксплуатации месторождения (участка недр).

11. При оценке устойчивости бортов и уступов карьеров, разрезов в массивах скальных и полускальных горных пород учитываются результаты исследований, характеризующих данный массив, к которым относятся:

пространственная ориентировка крупных разрывных нарушений между собой и поверхностью карьера, разреза;

густота, протяжённость и состояние основных систем трещин, их ориентировка относительно поверхности уступов и бортов;

физические характеристики горных пород;

прочностные характеристики горных пород;

прочностные характеристики контактов пород и других поверхностей ослаблений;

уровень подземных вод;

деформационные характеристики массива горных пород;

температурный режим, проявляющийся в непрерывном цикле оттаивания-замерзания горных пород;

параметры природного поля напряжений.

12. При оценке устойчивости бортов и уступов карьеров, разрезов в массивах дисперсных горных пород учитываются результаты исследований, характеризующие данный массив, к которым относятся:

набухание, снижение прочности и развитие локальных деформаций уступов и их групп;

развитие процессов суффозии, растворения, выветривания;

водонасыщенность пород, наличие водосборных площадей с затруднённой разгрузкой;

количество атмосферных осадков, характер дождей, мощность снегового покрова и продолжительность его таяния;

температурный режим района, глубина сезонного промерзания и оттаивания пород;

гранулометрический и минеральный состав пород;

число пластичности и показатель текучести (для глинистых пород);

относительная деформация набухания без нагрузки (для глинистых пород);

относительная деформация просадочности (для глинистых пород);

коэффициенты пористости и водонасыщения (для крупнообломочных грунтов и песков);

относительное содержание органического вещества;

компрессионные свойства пород;

температурно-прочностные свойства горных пород и контактов, криогенная структура, льдистость.

13. Расчёт устойчивости бортов, уступов, откосов проводится на стадии проектирования дифференцированно по классам массивов горных пород (коэффициенту крепости горных пород), которыми являются:

скальные породы, обладающие жёсткими структурными связями;

дисперсные породы с физическими, физико-химическими и механическими структурными связями, которые подразделяются на связные и несвязные (сыпучие);

мёрзлые породы, обладающие, наряду со структурными связями талых пород, криогенными связями (за счет льда). По типу структурных связей мерзлые породы подразделяются на следующие подклассы:

скальных мерзлых пород;

дисперсных мерзлых пород;

ледяных пород (породы только с криогенными связями).

III. Требования к инженерно-геологическому изучению и районированию массива горных пород

14. Программа инженерно-геологических работ разрабатывается и выполняется эксплуатирующими организациями на основании анализа факторов, определяющих устойчивость бортов, уступов, откосов на месторождении.

Объем и методика инженерно-геологических работ определяются в зависимости от степени сложности геологического строения месторождения и стадии его освоения на основании требований, установленных в приложении N 1 к Правилам.

15. Состав работ по инженерно-геологическому изучению должен включать:

для скальных и полускальных массивов: оценку ориентировки, густоты, протяжённости, шероховатости поверхностей основных систем трещин и наличия в них заполнителя, определение физических, прочностных и деформационных характеристик горных пород и контактов;

для массивов дисперсных пород: изучение гранулометрического и минерального состава, естественной влажности и пористости, определение сцепления, угла внутреннего трения, числа пластичности и показателей текучести, компрессионных свойств пород;

для мёрзлых дисперсных пород дополнительно проводится оценка температурно-прочностных свойств, криогенной структуры, льдистости, просадочности.

16. Инженерно-геологическое изучение скальных массивов в приконтурной зоне бортов карьеров и разрезов должно включать:

установление местоположения и ориентировки поверхностей ослабления относительно уступов с определением иерархических уровней;

определение параметров поверхностей ослабления каждого уровня иерархии, включая густоту, протяжённость и ширину раскрытия трещин, изменчивость элементов залегания, шероховатость, а также свойства заполнителя трещин;

определение прочностных и деформационных характеристик массива, структурных блоков горных пород и зон, примыкающих к крупным разрывным геологическим нарушениям.

17. Ширина приконтурной зоны, определяющей устойчивость борта карьера, разреза, в пределах которой должно выполняться инженерно-геологическое изучение массива, ограничивается геометрическими размерами призмы возможного обрушения и определяется при разработке программы инженерно-геологического изучения массива для каждого месторождения (участка недр) в зависимости от конструктивных параметров проектируемого карьера, разреза.

В пределах призмы возможного обрушения допускается формировать объекты инфраструктуры, нахождение людей и механизмов.

18. По мере углубки карьера, разреза, с периодичностью, установленной проектной документацией на производство маркшейдерских работ, проводится картирование уступов на каждом вновь вскрытом горизонте с нанесением выявленных структурных элементов на горно-графическую документацию.

Источник

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего

«НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ «ГОРНЫЙ»

На правах рукописи

ПАНЧЕНКО Алексей Викторович

МАРКШЕЙДЕРСКАЯ ОЦЕНКА УСТОЙЧИВОСТИ КРИВОЛИНЕЙНОГО

В ПЛАНЕ БОРТА КАРЬЕРА

Специальность 25.00.16 – Горнопромышленная и нефтегазопромысловая геология, геофизика, маркшейдерское дело и геометрия недр

Научный руководитель:

доктор технических наук

Мустафин Мурат Газизович

ДИССЕРТАЦИЯ

на соискание ученой степени кандидата технических наук Санкт-Петербург –

СОСТОЯНИЯ БОРТОВ КАРЬЕРОВ КРИВОЛИНЕЙНОЙ ФОРМЫ В ПЛАНЕ..

2.1 Особенности деформирования прибортового массива горных пород с разной криволинейностью борта в плане

Моделирование деформаций борта карьера с разными свойствами горных 2. пород и геометрией в плане

Расчет поправочных коэффициентов за величину угла откоса борта 2. карьера

Расчет поправочного коэффициента сцепления

2. Определение добавочного угла в геометрические параметры откоса. Учет криволинейности локальных участков борта

Определение закона распределения деформаций по фронту борта карьера

Выводы по второй главе

ГЛАВА 3 РАЗРАБОТКА МЕТОДИКИ РАСЧЕТА ПАРАМЕТРОВ

УСТОЙЧИВЫХ БОРТОВ С УЧЕТОМ ИХ КРИВОЛИНЕЙНОСТИ

Интерпретация показателей криволинейности карьера на планах горных работ для практического использования

Схема расчета параметров бортов карьера прямоугольной формы в плане

Схема расчета параметров бортов карьера круглой формы в плане. Схема расчета параметров бортов карьера на локальных участках криволинейности

Схема расчета параметров бортов карьера эллипсоидальной формы в плане

Схема расчета параметров бортов карьера, прямолинейные участки которых примыкают к закруглениям

Пример расчета параметров бортов сложнокриволинейного карьера в плане

Сравнение полученных результатов с существующими методиками определения устойчивости криволинейных бортов

Расчет эффекта от оптимизации геометрии карьера

3.10 Выводы по третьей главе

ГЛАВА 4 АПРОБАЦИЯ РАЗРАБОТАННОЙ МЕТОДИКИ НА ПРИМЕРЕ

РУДНЫХ МЕСТОРОЖДЕНИЙ МАГАДАНСКОЙ ОБЛАСТИ

Обоснование расчетных показателей физико-механических свойств пород для оценки устойчивости бортов, уступов открытых горных выработок. Расчет устойчивости бортов карьера Биркачан

Расчет устойчивости бортов карьера Сопка Кварцевая

Расчет устойчивости бортов карьера Цоколь

Анализ мер повышения безопасности и меры контроля устойчивости бортов карьеров

Выводы по четвертой главе

СПИСОК ЛИТЕРАТУРЫ

ВВЕДЕНИЕ

Актуальность темы исследования Многообразие горно-геологических условий разработки месторождений полезных ископаемых открытым способом предполагает различные формы контуров бортов карьеров. Одной из главных задач при этом является обеспечение его устойчивости. Решение этого вопроса, в основном, выполняется для двумерного случая (плоская задача), и в этой связи криволинейность бортов карьеров в плане не учитывается.

В настоящее время благодаря компьютерным технологиям становится возможным развитие исследований по учету кривизны бортов карьера. Получение зависимостей распределения деформаций и напряжений в породах борта карьера от геометрических параметров и физико-механических свойств позволяет получить отличия криволинейного в плане борта от прямолинейного.

Сопоставление эмпирических данных и результатов моделирования на основе метода конечных элементов, реализованного в современных программах, создают хорошие предпосылки к решению вопроса оценки устойчивости криволинейных участков борта.

Большой вклад в развитие методов расчета устойчивости бортов карьеров внесли такие ученые, как: Фисенко Г.Л., Борщ-Компаниец В.И., Попов И.И., Сапожников В.Г., Пушкарев В.И., Галустьян И.Л., Ермаков И.И., Мочалов А.М., Пустовойтова Т.К., Шпаков П.С., Макаров А.Б., Незаметдинов Ф.К., Мустафин М.Г., Туринцев Ю.И., Певзнер М.Е., Куваев Н.Н. и многие другие. Разработанные схемы учета криволинейности бортов карьеров весьма важны при оценке их устойчивости и позволили обеспечить рациональное ведение горных работ, однако они базируются на эмпирических данных 30-40-летней давности и поэтому имеют запас для условий, отличных от тестовых случаев. В работе, опираясь на результаты предыдущих исследователей, фактических данных о деформировании прибортового массива, представлена методика учета криволинейности борта карьера в плане при расчете его устойчивости.

Цель диссертационной работы состоит в повышении эффективности разработки месторождений полезных ископаемых открытым способом за счет создания методики, учитывающей криволинейность борта карьера в плане.

Основные задачи

криволинейности и формы карьера в плане и разработать методику исследований;

2. Провести математическое моделирование деформационного процесса прибортового массива карьера различной формы в плане для выявления коэффициента кривизны;

3. Разработать методику оценки устойчивости борта карьера с учетом криволинейности его границ в плане;

4. Провести экспериментальную проверку разработанной методики.

Идея работы заключается в выявлении, на основе моделирования с использованием объемной упругой задачи, деформационных показателей, характеризующих различия деформационного процесса на участках борта карьера разной кривизны и учете этих изменений в виде коэффициента в известных формулах расчета устойчивости бортов карьера Методы исследований. При выполнении исследований использовался комплекс методов: анализ и обобщение результатов ранее выполненных исследований, в том числе представленных в нормативно-методических документах; инструментальные наблюдения в натурных условиях, математическая обработка результатов экспериментальных данных, компьютерное моделирование напряженно-деформированного состояния прибортового массива на основе метода конечных элементов, сравнение натурных, лабораторных и расчетных данных результатов исследований.

Научная новизна:

1. Зависимости смещений борта карьера от его кривизны в плане и физикомеханических свойств пород;

2. Алгоритм расчета коэффициента кривизны, учитывающего нелинейность процесса деформирования борта карьера и произвольную форму плоскости скольжения призмы обрушения.

Научные положения, выносимые на защиту:

1) При разработке месторождений полезных ископаемых открытым способом значение устойчивого угла откоса карьера зависит от его формы в плане и соотношений геометрических параметров и может отличаться на разных участках весьма существенно до 30% в зависимости от степени условной кривизны, что позволяет уменьшить объемы вскрышных работ на 15-20%.

2) Планирование маркшейдерских наблюдений за устойчивостью борта карьера целесообразно выполнять в зонах с минимальным коэффициентом запаса устойчивости, определенных с учетом кривизны карьера в плане.

Практическая значимость:

1. Разработана методика учета криволинейности борта карьера при оценке его устойчивости для широкого спектра геомеханических параметров.

2. Даны рекомендации по расположению наблюдательных станций на карьерах с выраженной криволинейностью в плане.

Реализация результатов работы. Полученные результаты могут быть использованы на действующих карьерах, в учебных учреждениях, проектных организациях, а также в научно-исследовательских институтах.

Личный вклад автора:

1. Участие в постановке задач и формулировании основных выводов по исследованию.

2. Расчет и анализ деформационного процесса объемных и плоских моделей бортов карьеров разной геометрии с использованием современных программных комплексов.

3. Установление зависимости между устойчивостью откоса уступа и показателем криволинейности борта в плане и глубины разработки.

4. Разработка методики определения устойчивого состояния криволинейных участков бортов в плане.

5. Сбор и анализ данных по изучению деформационного процесса на карьерах ОАО «Полиметалл», ОЗРК.

Публикации. Основное содержание работы

отражено в 4 публикациях, из них 3 в журналах, включенных в перечень ведущих рецензируемых научных журналов и изданий, определяемый ВАК Минобрнауки России.

Структура и объем работы. Диссертация состоит из введения, четырех глав, заключения, библиографического списка (102 литературных источников), изложенных на 119 страницах машинописного текста, содержит 10 таблиц, рисунков.

Автор выражает благодарность за оказанную помощь на разных этапах выполнения работы научному руководителю, д.т.н. Мустафину М.Г., заведующему кафедрой маркшейдерского дела, д.т.н. Гусеву В.Н., главному маркшейдеру ОЗРК Шубину А.Л. Благодарю сотрудников кафедры маркшейдерского дела за полезные советы, критические замечания и содействие в подготовке диссертационной работы.

Основное содержание работы В первой главе показано состояние изученности вопроса, изложены методы расчета устойчивости бортов карьера, приводятся существующие схемы учета криволинейности в плане бортов карьеров, обоснована актуальность темы и сформулированы основные задачи исследований.

Во второй главе описана методика исследований деформирования прибортового массива горных пород с разной криволинейностью в плане при учете физико-механических свойств на основе моделирования, обосновывается расчет добавочного угла и поправочных коэффициентов в геометрические параметры устойчивого борта карьера.

криволинейных участков бортов карьеров, произведено сравнение получаемых результатов с существующими методиками определения устойчивости криволинейных бортов.

В четвертой главе приведена реализация изложенного подхода в натурных условиях, рассмотрены три карьера с разными геометрическими и физикомеханическими параметрами, выполнен расчет устойчивости бортов по разработанной методике, разработаны мероприятия по контролю устойчивости бортов карьеров.

ГЛАВА 1 СОСТОЯНИЕ ИЗУЧЕННОСТИ ВОПРОСА

Одновременное становление горной геомеханики на открытых горных работах как самостоятельного направления науки, работа лабораторий ВНИМИ (Г. Л.

Фисенко), Унипромеди (Ю. И. Туринцев), ИГД МЧМ СССР (В. Г. Зотеев), ВИОГЕМа (А. И. Ильин), ИГД им. Скочинского (А. М. Демин), ГИГХа (М. Е.

Певзнер [62] ), Укрниипроекта (Н. Н. Куваев [40] ), СГИ (В. В. Камшилов, Н. Д.

Ипполитов, А. В. Шабурников, А. П. Бадулин [4] ), КПИ (М. Л. Рудако, И. И.

Попов [64, 65] ), обеспечило полноту исследований.

экономической эффективности отделами горного планирования предприятий рассчитываются модели карьеров с максимально возможными углами погашения.

При этом учет неравномерного действия сил бокового распора (в местах отличных от прямолинейных участков) позволяет варьировать формой выемки в плане и по высоте. Особенности строения месторождений нередко позволяют это сделать, и возникает возможность оставить значительную часть вскрыши в бортах карьера.

АНАЛИЗ ИССЛЕДОВАНИЙ В ОБЛАСТИ УСТОЙЧИВОСТИ

БОРТОВ КАРЬЕРОВ

1.1.1 НОРМАТИВНО-МЕТОДИЧЕСКИЕ ДОКУМЕНТЫ,

РЕГЛАМЕНТИРУЮЩИЕ ОЦЕНКУ УСТОЙЧИВОСТИ БОРТА КАРЬЕРА

«Инструкция по наблюдениям за деформациями бортов, откосов уступов и отвалов на карьерах и разработке мероприятий по обеспечению их устойчивости» [33] является документом, регламентирующим оценку устойчивости бортов карьеров, включает весь комплекс маркшейдерских и инженерно-геологических наблюдений, необходимых для решения вопросов по обеспечению устойчивости откосов, и мероприятий по предотвращению нарушений устойчивости откосов и обеспечению безопасности работ на действующих карьерах.

Разработке общих мер по обеспечению устойчивости предшествуют работы по исследованию оптимальных углов наклона уступов и генеральному углу погашения бортов карьера. При их отсутствии величины принимаются в соответствии с рекомендуемыми значениями, приведенными в нормах технологического проектирования горнорудных предприятий с открытым способом разработки ВНТП 35-86, Едиными правилами безопасности при разработке месторождений полезных ископаемых открытым способом ПБ 03-498и Правилами обеспечения устойчивости на угольных разрезах [66].

Дополнительные данные по оценке устойчивости бортов карьера представлены в многочисленных правилах и методических указаниях [44, 45, 81, 86, 87] Приведены обоснования требований по определению устойчивости, объемы инженерно-геологических работ и пр. Все эти документы представляют собой методическую основу для разработки действующей инструкции.

Методические указания по определению углов наклона бортов, откосов уступов и отвалов строящихся и эксплуатируемых карьеров [44] одна из работ, наиболее полно представляющих процесс расчета параметров устойчивого борта с учетом его криволинейности в плане. В указаниях рассмотрены ряд схем, описывающих методику расчета откосов разной формы в плане, условия применения для слоистого и неслоистого массива.

1.1.2 НАУЧНО-МЕТОДИЧЕСКИЕ ЛИТЕРАТУРНЫЕ ИСТОЧНИКИ

По вопросам устойчивого состояния бортов уступов карьеров представлено большое количество литературы. Среди исследователей можно выделить работы Г.Л. Фисенко [86, 87, 89, 90], Г. В. Верещагин, Г.Н. Кузнецов [45], Куваев Н. Н.

Среди научно-методических литературных источников можно выделить «Устойчивость бортов карьеров и отвалов» под редакцией Г.Л. Фисенко, 1965 г.

[90] и «Геомеханика открытых горных работ» под редакцией А.М Гальперина, 2003 г. [10] В этих трудах приведен анализ процессов нарушения устойчивости бортов карьеров, изложены теоретические основы прогноза геомеханических процессов в бортовых массивах, описаны технологические и специальные мероприятия по направленному изменению состояния массива. Вопросу изогнутости бортов в плане отведено особое место. Г.Л. Фисенко отмечает необходимость применения особых схем по определению углов наклона бортов карьеров, имеющих в плане круглую или овальную форму. В издании [10] вопрос определения устойчивости бортов карьеров криволинейной формы в плане рассмотрен более детально на примере откосов угольных разрезов. Учитывается многообразие форм в плане для расчета геометрических параметров, условия применения и, по сути, содержит в себе основные выдержки из правил ВНИМИ [66].

1.2 ПРЕДПОСЫЛКИ К РАЗРАБОТКЕ МЕТОДИКИ ПО УЧЕТУ

КРИВОЛИНЕЙНОСТИ БОРТОВ В ОПРЕДЕЛЕНИИ УСТОЙЧИВОСТИ

Вопрос о влиянии формы карьера на его устойчивость поднимался в работах ВНИМИ, СГИ и Унипромеди, где на основе графиков зависимости геометрических параметров бортов карьеров и при учете физико-механических свойств пород описываются схемы определения параметров откосов с разной формой карьеров в плане [10,33, 44, 81]. При этом в объемном виде фактор криволинейности борта карьера и его влияние на величину коэффициента запаса устойчивости не рассматривалась. Вместе с тем знание о его влиянии на деформационный процесс весьма важно, так как позволяет более рационально проектировать горные работы, варьируя параметрами карьера. Так, например, для карьеров круглой формы в плане коэффициент запаса устойчивости борта, очевидно, будет выше, чем откос карьера протяженного, прямоугольного в плане, с размерами малой стороны равной диаметру круглого [33, 66, 81, 90].

На производстве, в результате традиционного анализа устойчивости откосов не учитывается или учитывается не полностью ряд параметров. Поиск наиболее слабой поверхности производят с помощью маркшейдерских наблюдений за сдвижением и деформациями бортов и откосов или на основе общих представлений о сдвижении и геомеханике бортов [11, 14, 54, 80]. При этом, как правило, рассматривается плоское решение задачи о деформировании борта. Но при постоянно меняющемся направлении изогнутости борта меняется и величина сопротивления смещению породного массива. В этих условиях использование двумерных задач будет не совсем корректно.

В работе [55] отмечают, что результат инструментального контроля сдвижения пород у карьеров сложной конфигурации в плане свидетельствует о недостаточности контроля напряженно-деформированного состояния пород по профильным линиям, заложенным по главным сечениям месторождения. В условиях действия анизотропного поля напряжений, измеренные таким образом деформации, будут сильно отличаться от фактических в виду таких факторов как направление и месторасположение профильной линии, степень криволинейности борта и, как следствие, несоответствие теоретических представлений о закономерностях деформирования породного массива.

Для более точного прогноза физико-механических явлений необходимо уточнить ряд параметров модели, таких как направления действий и величины главных векторов тектонических напряжений, величин модуля деформации для отдельных участков массива горных пород, произвести оценку стабильности структурных нарушений и их интенсивность на разных участках, уточнить постоянно изменяющиеся геометрические параметры техногенных объектов и проч. Но из-за громоздкости вычислений, до недавнего времени, учетом этих параметров пренебрегали [2]. С развитием компьютерных программных продуктов, стало возможным сделать предрасчет напряженно- деформированного состояния массива в условиях его сложного строения. Более того, многие программы, основанные на наиболее популярном методе конечных элементов, позволяют произвести обоснованный расчет ещё до проведения выработки. Что определяет дополнительные преимущества и подчеркивает необходимость в пересмотре существующих методов расчета.

1.2.1 СУЩЕСТВУЮЩАЯ МЕТОДИКА УЧЕТА КРИВОЛИНЕЙНОСТИ

При открытом способе разработки месторождений полезных ископаемых основным вопросом является обеспечение устойчивости бортов карьеров.

Исследователи влияния криволинейности борта на его устойчивость отмечают, что степень действия сил бокового распора, возникающих за счет дополнительного сопротивления смещения призмы обрушения, зависит от конфигурации борта в плане, горно-геологического фактора и соотношения протяженности откоса и его высоты [10, 81, 86, 87, 90]. Устойчивость угловых участков бортов карьеров вытянутой формы и бортов карьеров круглой или овальной форм в плане существенно возрастает. По сравнению с прямолинейными в плане бортами в перечисленных случаях возникает дополнительное сопротивление смещению призмы обрушения, создаваемое силами бокового распора (гор =Н, где — коэффициент бокового распора; — плотность породы; Н — высота борта).

Задача использования геометрии карьера в оптимизации техникоэкономических показателей неоднократно ставилась исследователями. В методических указаниях 1972 года [44] отмечается важность поставленного вопроса. На основании ряда схем, созданных с учетом геологического строения пород, предлагаются варианты расчета устойчивости откосов с разной криволинейностью в плане, указаны условия их применимости и порядок вычисления поправок. Общая суть выработанных методик сводилась к выявлению на первых этапах по схемам расчета угла наклона прямолинейного в плане борта плоского профиля и последующим определением поправки к этому углу за кривизну борта в плане.

Вопрос учета криволинейности бортов карьеров в плане был детально рассмотрен ВНИМИ, определение параметров устойчивости, в этих случаях, корректируются при помощи графиков, построенных на основе моделирования методом эквивалентных материалов. На рисунке 1.1,а – представлен график зависимости угла наклона ’ борта карьера круглой формы от условного радиуса кривизны нижнего контура R для карьера круглой формы. Величина ’ определяется по значениям R/Н (Н — глубина карьера) и угла наклона прямолинейного в плане борта плоского профиля. Величина находится по графику плоского откоса. Для карьера с квадратной подошвой в случаях, когда линейный размер подошвы меньше двух наклонных высот борта ( ) или имеются зажатые участки бортов, протяженность которых l’=l/H90 также не превышает, используется график на рисунке 1.1, б. После определения поправки угол наклона борта на зажатом участке определяется в виде ’=+.

В случаях, когда в бортах криволинейных в плане карьеров поверхности ослабления большого протяжения отсутствуют, локальны и не падают в сторону выемки, применяют типовые схемы определения углов наклона бортов, вводя поправки к углу наклона прямолинейного борта (таблица 1.1).

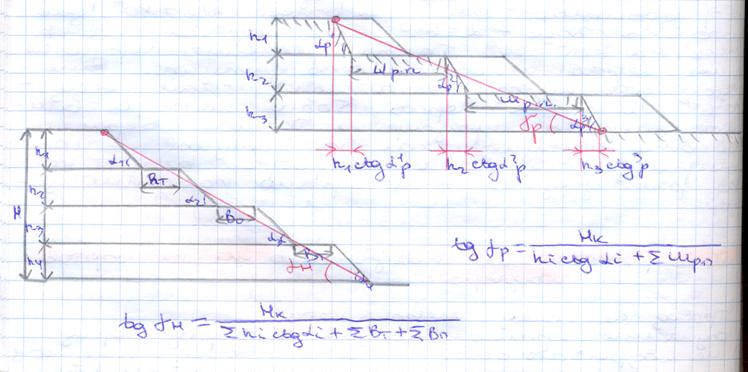
Рисунок 1.1 – Определение углов наклона бортов карьеров с учетом их а — график зависимости угла наклона борта от его кривизны в плане; б— определение поправки с учетом условной длины l’ зажатого участка Схема 1. Применяется для определения углов наклона бортов в условиях карьеров, контуры которых в плане близки к окружности. Порядок расчета следующий. Определяют угол наклона пл, прямолинейного в плане борта плоского профиля с заданным коэффициентом запаса устойчивости откоса и вычисляют поправку к этому углу за счет круглой формы борта в плане 1 с использованием графика поправок (рисунок 1.2). Для этого измеряют средний радиус кривизны нижней бровки карьера Rн, вычисляют условную его величину R’= Rн/Н90 и на оси ординат отыскивают. График поправок 1 действителен при условии где H’ — условная высота, равная H/H90.

Рисунок 1.2 – Зависимость поправки к углу наклона борта, круглого в плане, Если R’ меньше минимально допустимого значения, то для установления профиля борта в разрезе применяют дополнительные графики предельных очертаний откосов вогнутого профиля круглых выемок в соответствии с методическими указаниями ВНИМИ.

Если борт карьера круглой формы прорезает траншея на глубину не менее 2/3 его высоты, то угол наклона борта принимается переменным — от пл:

(определяется по графику плоского откоса на границе прямолинейных контуров траншеи с круглыми контурами карьера) до (определяется с учетом поправки 1 график на рисунке 1.1).

Схема 2. Используется для определения углов наклона прямолинейных в плане участков бортов, «зажатых» на его закруглениях. Общую длину «зажатого»

(в том числе прямолинейного) участка l’ определяют по формуле кривизны нижней бровки борта; l —длина прямолинейного участка.

По графику поправок на рисунке 1.3 находят значение 2 и определяют угол наклона борта пл с заданным коэффициентом запаса устойчивости откоса, используя для этого график плоского откоса. Общий угол наклона борта вычисляют по формуле:

Схема 3. Применяется для определения углов наклона бортов с квадратным дном карьера и на участках, «зажатых» их закруглениями.

Определяют параметры устойчивости бортов в такой последовательности. С помощью графика определения поправок 2 (рисунок 1.3) вычисляют угол наклона борта на прямолинейных участках с учетом степени их «зажатости»:

Затем, используя график поправок на рисунке 1.3, определяют угол наклона борта на закруглениях:

Рисунок 1.3 – Зависимость поправки к углу наклона борта карьера от длины «зажатого» участка борта l при : 1—10°; 2—15°; 3—20°; 4— 25°;

На диагонали квадрата находят центр закругления на расстоянии =R’H от угла квадрата по диагонали (см. таблицу 1.1, схема 3). Верхняя бровка отстраивается радиусом до пересечения с бровкой его прямолинейной части.

Таблица 1.1 – Схема расчета карьерных откосов с учетом криволинейности бортов в плане Круглопрямолинейная с дна карьера l меньше зависимости Если верхняя прямолинейная бровка не пересекается с криволинейной, то производится перерасчет радиуса кривизны по формуле Углы наклона борта карьера в случае, когда линейные размеры его дна более двух наклонных высот, определяют в такой последовательности: на прямолинейных участках устанавливают пл, на закруглениях находят поправку 1 для допустимого радиуса R’ и центр закругления описанным ранее способом, а радиус закругления верхней бровки вычисляют по формуле:

Если дуга радиуса R не пересекает верхний контур прямолинейной части борта, то производят перерасчет радиуса по формуле:

Схема 4. Применяется для определения углов наклона бортов карьеров в плане эллипсоидальной формы и с участками борта вогнутого профиля, дня которых можно подобрать свои радиусы закругления бровок поверху RB и понизу Порядок определения параметров бортов карьеров эллипсоидальной формы следующий. Находят центры и величины радиусов закруглений RB и RH.

Вычисляют значения H90 и условные радиусы закругления бровок по дну карьера R’=R/H90 для каждого его участка. Определяют углы наклонов криволинейных участков бортов карьера. Верхние бровки криволинейных участков бортов отстраивают радиусами Ri=RH+Hctg(пл + 1), затем контур карьера в плане плавно сглаживается.

Если борт рассечен глубокой траншеей, то угол наклона борта принимают переменным — от (на границе прямолинейного участка траншеи с криволинейными бровками карьера) до.

Определение параметров бортов карьера по схеме 5 производится в следующей последовательности (рисунок 1.4):

а) по графику поправок на рисунке 1.2 по относительному радиусу кривизны R’=R/H90 определяют поправку ;

б) при 0 10 угол наклона в среднем сечении закругления ОС определяют по формуле:

где – угол между простиранием сопряженных прямолинейных бортов;

на остальных сечениях закругления угол наклона принимается переменным – от закругления;

в) при 0 10 на средней части закругления на участке от сечения OD до сечения OB, расположенных к крайним сечениям прямолинейных участков OA и OE под углом 45 (рисунок 1.5), угол наклона борта принимается равным ; между сечениями OB и OA, OD и OE – угол наклона плавно уменьшается от Рисунок 1.5 – Карьер круглой формы, борта которого рассечены вертикально Схема 6. Карьер круглой формы, прорезанный глубокой траншеей не менее чем на 2/3 глубины карьера.

Порядок установление параметров бортов карьера по схеме 6 следующий:

а) карьер делят на две половины таким образом, чтобы траншея оказалась посередине одной из частей (рисунок 1.6).

Рисунок 1.6 – Карьер круглой формы, прорезанный глубокой траншеей б) для половины карьера, борт которой не прорезается траншеей, поправку 0 определяют так же, как по схеме 1 (рисунок 1.2) в) на прорезанной половине угол следует принимать переменным – от пл на границе с траншеей до на границе со второй половиной борта.

Для условий схем 2,3,4, если борт рассечен глубокой траншеей, для не рассеченной половины борта поправка 0 определяется по соответствующей схеме; в прорезанной половине угол наклона борта переменный – от пл на границе с траншеей до на границе со второй половиной борта.

Приведенные выше схемы по определению поправок в параметры устойчивости бортов карьеров с разной криволинейностью в плане, как отмечают авторы [66], применимы для неслоистого массива, где нет поверхностей ослабления, а так же при условии, когда имеющиеся поверхности ослабления и зоны анизотропии прочности (зоны разлома, сланцеватости) имеют локальное распространение и не рассекают борт.

В слоистом массиве, где сцепление по контактам слоев, как правило, значительно меньше сцепления в массиве, различают три случая залегания пород:

а) горизонтальное и пологое – угол падения слоев до б) наклонное и крутое – угол падения слоев 20- в) весьма крутое и вертикальное – угол падения слоев 80- При горизонтальном и пологом залегании слоев слоистого массива они не рассекаются бортом карьера круглой формы, а боковой распор в породах, слагающих борт карьера, действует как в неслоистом массиве. Поэтому в горизонтальном и пологом залегании слоев для определения угла наклона криволинейного борта следует применять вышеприведенные расчетные схемы.

При вертикальном залегании слоев при круглой и овальной форме карьера бортом на некоторых участках слои рассекаются, и боковой распор по контактам слоев уменьшается; на этих участках параметры борта принимаются равными прямоугольному в плане борту небольшой протяженности.

Границы участков, на которых угол наклона борта круглой формы равен углу наклона прямолинейного в плане борта, определяются следующим образом:

простиранию борта, граничное сечение ограничивается углом трения по контактам ’ (на рисунке 1.6) граничные сечения для круглого карьера обозначены ОА, OD, OE, OH);

б) со стороны участка, где простирание слоев параллельно простиранию борта, граничные сечения проводят через точки пересечения верхней бровки слоем, пересекающим откос в сечении, нормальном к простиранию слоев, на высоте НН (НН – наклонная высота борта) от нижней бровки борта (на рисунке 1.6 этими сечениями будут ОВ, OC, OF, OQ).

На участках AH, BC, DE, QF угол наклона борта определяют как в схеме для случая сопряжения двух прямолинейных зажатых откосов.

На участках AB, CD, EF, QH угол наклона борта принимается с поправкой за кривизну, равной половине поправки на участках AH, BC, DE, OF.

При наклонном и крутом залегании слоев (20 80) угол наклона борта карьера круглой и овальной формы определяют в следующем порядке:

а) по главным сечениям OA, OB, OC, OD (рисунок 1.7) угол наклона Рисунок 1.7 – Карьер круглой формы, при наклонном и крутом залегании слоев вычисляют, как для прямолинейного в плане борта плоского профиля.

б) по вычисленным углам наклона строят верхний контур борта карьера для главных сечений – пунктирный контур на рисунке 1.7.

в) по графику (рисунок 1.2) определяют поправку к углу наклона за кривизну борта 0 – она одинакова для всех главных сечений OA, OB, OC, OD;

г) по сечению ОВ угол наклона борта ОВ принимают равным д) по сечениям OF и OE угол наклона принимают равным ж) при 0 10 на участке MN, ограниченном центральным углом 2’, угол з) при 0 10 на участке FK и EL угол наклона переменный от В слоистом массиве на участках, где имеется боковой распор, поправку по графику (рисунок 1.2) определяют по условному радиусу, полученному по характеристикам n и kn без учета слоистости:

R’= Rн/Н90, где Rн – радиус выемки по подошве карьера.

При других схемах определения параметров криволинейного в плане борта карьера в слоистом массиве условия рассечения слоев бортом, когда уменьшается боковой распор, возникают также только при наклонном, крутом и вертикальном залегании слоев на отдельных участках определяемых аналогично рассмотренным выше условиям круглого карьера.

Увеличение добавочного угла в зависимости от степени зажатости рекомендуется вычислять по установленной эмпирической зависимости:

где – добавочный угол откоса; H – высота откоса, м; L – длина зажатого откоса, м.

Данная зависимость, представленная на рисунке 1.8, позволила определять величины добавочных углов в широком диапазоне значений угла внутреннего трения с точностью 1 при высокой надежности.

Таким образом, угол откоса на закруглении борта определяется как сумма углов – полученного из решения плоской задачи пл и добавочного угла.

Авторы отмечают, что эффективность зажима ощутимо проявляется при Рисунок 1.8 – Определение показателя зажатости Отметим, что общий угол зажатого откоса не должен превышать углов для смежных участков, выполняющих граничное условие.

Анализ существующей научно-технической и нормативной документации в области исследований криволинейности бортов уступов в плане и использования геометрии карьера для горнотехнических нужд позволяет сделать вывод о важности этого вопроса и его частичном решении для определенных условий.

Вместе с тем надо отметить, что вопрос решался на базе фактического материала, который охватывает лишь небольшую часть возможных условий разработки. При этом в качестве дополнительных доказательств использовались результаты экспериментальных исследований по упрощенным моделям эквивалентных материалов, что говорит о недостаточной изученности данного вопроса.

Требуется углубленное изучение поведения массива в рамках решения объемной устойчивости бортов карьера.

1.2.2 ИСПОЛЬЗОВАНИЕ МЕТОДОВ РАСЧЕТА ДЕФОРМИРОВАННОГО

СОСТОЯНИЯ МАССИВА ГОРНЫХ ПОРОД ДЛЯ ОЦЕНКИ

УСТОЙЧИВОСТИ БОРТА КАРЬЕРА

Методы расчета устойчивости откосов позволяют в количественной форме установить влияние различных процессов на состояние массива горных пород и оценить эффективность мероприятий по снижению их негативной роли.

В настоящее время существует схема классификации методов расчета устойчивости откосов, предложенная М. Е. Певзнером, охватывающая практически все разработки российских и зарубежных авторов. Классификация составлена по схеме: класс методов — группа методов — основной метод (методы) группы — расчетные способы и схемы, использующие основной метод.

Основным классификационным принципом для выделения классов методов принято определение параметров устойчивого откоса. Соответственно выделено пять классов методов.

1. Класс А (основной метод В.В, Соколовского, расчетные способы и схемы И.С. Мухина и А.И. Срагович, А.М, Сенкова, Г.Л. Фисенко, В.Т. Сапожникова, предусматривающие построение контура откоса, являющегося внешней границей зоны, во всех точках которой удовлетворяется условие предельного равновесия.

удовлетворяется равенство угла наклона касательной углу сопротивления сдвигу.

К классу Б отнесены два метода, характеризующиеся разбивкой откоса на горизонтальные слои и определением устойчивого угла наклона каждого слоя с учетом массы вышележащих пород.

массиве откоса поверхности скольжения, вдоль которой удовлетворяется условие предельного равновесия.

В классе В выделено пять групп методов: в первой группе расчет устойчивости откоса производится на основе плоской поверхности скольжения (Л,Н. Бернацкого, П.Н. Цымбаревича), во второй —круглоцилиндрической (В.

Феллениуса, Д. Тейлора, Н. Янбу, М.Н. Гольдштсйна, О. Фрелиха, А. Како, И.В.

Федорова), в третьей — логарифмической спирали (Г. Крея — К. Тервдги, Р.Р.

Чугаева, А. Бишопа, Г.М, Шахунянца, Е. Спенсера, Н. Моргенштерна — В.

Прайса), в четвертой — поверхности скольжения сложной криволинейной формы (Л. Рендулика, Н.П. Пузыревского — П.И. Кожевникова, КХС Козлова — В.П.

Будкова, Г.Л. Фисенко, Л.В, Савкова, А.Г. Дорфмана, конечных элементов), в пятой — поверхности скольжения ломаной формы (А.П. Ясюнас, Н.Н. Маслова, Р.Р, Чугаева). Кроме того, во второй группе методов выделены две подгруппы; в первой учитывается условие равновесия откоса, а во второй — условие равновесия отдельных вертикальных отсеков.

Класс Г (методы ВНИМИ — Г.Л. Фисенко, Н.Н. Куваева, Э.Л.

ВНИИЦветмета, П.Н. Панюкова — МГИ, И.И. Попова и Р.П. Окатова — КарПи) — методы, предусматривающие построение в массиве поверхности скольжения, вдоль которой удовлетворяется условие специального предельного равновесия.

Класс Г включает в себя методы, в которых определение сдвигающих и удерживающих сил производится с учетом прочностных характеристик, действующих по поверхности ослабления откоса. В этот класс входит также группа методов, учитывающих объемный характер процесса разрушения и форму призмы обрушения.

5. Класс Д — методы, предусматривающие вероятностную оценку устойчивости откосов на основе статистических оценок определяющих факторов.

Предложено проводить анализ методов расчета устойчивости откосов на основе двух групп критериев: общих и частных. Общие критерии определяют обоснованность метода в теоретическом отношении, частные — возможность его использования в конкретных условиях.

Для практических расчетов используются инженерные методы, основанные на установлении условий предельного равновесия по поверхностям скольжения, положение которых определяется путем последовательных приближений.

В этом случае должны соблюдаться три условия статики сыпуче-связной среды [20]:

равенство моментов сдвигающих и удерживающих сил относительно дуги скольжения;

равенство проекций вертикальных составляющих удерживающих и сдвигающих сил;

равенство проекций горизонтальных составляющих удерживающих и выполняются.

К числу инженерных относятся методы алгебраического суммирования сил по круглоцилиндрическим и монотонным криволинейным поверхностям и многоугольника сил. Используется также комбинации этих методов и методов предельного напряженного состояния для решения плоской задачи. Практика расчетов показала [81, 98], что данный метод можно использовать при оценке устойчивости откосов, длина L которых в 2-3 раза больше его высоты Н, а потенциальная поверхность скольжения имеет вид плавной кривой. В этом методе предполагается, что призма возможного обрушения деформируется как единое целое и реакции между блоками не учитываются. Это приводит к тому, что рассчитанный коэффициент запаса на 3 – 20% меньше фактического. Однако при небольшой высоте откосов (до 100 метров) в рыхлых породах, при небольших углах внутреннего трения (20) данный метод дает приемлемые результаты.

На предположении круглоцилиндрической поверхности скольжения Круглоцилиндрическая или монотонная криволинейная поверхности скольжения обычно образуются в массивах, сложенных однородными породами, при горизонтальном залегании слоев с близкими по значению прочностными характеристиками, а также при обратном падении слоев в сторону массива.

Принимается, что ограниченный поверхностью скольжения массив представляет собой «жесткий клин», а ожидаемое смещение массива рассматривается как вращение «жесткого клина» вокруг оси, параллельной откосу и служащей осью кругового цилиндра (рисунок 1.9).

Рисунок 1.9 – Вращение «жесткого При этом в плоской задаче круглоцилиндрическая поверхность скольжения превращается в дугу окружности АСВ, а ось цилиндра – в точку О (рисунок 1.10).

Так же при расчетах устойчивости применяют метод алгебраического сложения сил. Сдвигающий момент М определяется алгебраическим сложением моментов от веса отдельных блоков Рi, на которые разделяют призму возможного обрушения:

Из рисунка 1.10 имеем:

плечо силы Pi; i – угол наклона поверхности скольжения в точке, лежащей на одной вертикали с центром тяжести элементарного блока.

Момент сил, удерживающий призму возможного обрушения от вращения сцепления; L – длина дуги АСВ, численно равная площади поверхности скольжения цилиндрического тела длиной 1 м.

Силы трения по поверхности скольжения определяются как произведение коэффициента внутреннего трения (f = tg, где – угол внутреннего трения) пород на сумму нормальных составляющих сил массы отдельных блоков:

Следовательно, алгебраическое сложение сдвигающих и удерживающих сил поверхности скольжения. Из условия равновесия имеем В общем случае коэффициент запаса устойчивости:

Влияние погрешностей определения прочностных характеристик пород, роль динамических нагрузок при массовых взрывах, снижение прочности пород с течением времени в расчетах параметров борта учитывают посредством коэффициента запаса устойчивости:

внутреннего трения пород по поверхности скольжения.

Далее, получив механические характеристики вдоль линии скольжения как средневзвешенные и как расчетные, используют их в расчетах устойчивости уступов, бортов карьеров и отвалов.

При построении потенциальную поверхность скольжения делят на три части (рисунок 1.11):

— вертикальная плоскость отрыва СD, которая определяется глубиной где – угол трения, kм – сцепление в массиве, – удельный вес породы;

Наклонная площадка скольжения ЕD отклоняется от вертикали на угол Рисунок 1.11 – Схема построения потенциальной поверхности скольжения в однородном прибортовом массиве.

Круглоцилиндрическая поверхность скольжения АЕ пересекает основание откоса под углом к его плоскости.

Ширину призмы возможного обрушения вычисляют по формуле:

В формулах определения Н90 и ВС в качестве и k принимают средневзвешенные их значения.

Поиск наиболее слабой поверхности возможно еще и через маркшейдерские наблюдения за сдвижением и деформациями бортов и откосов.

Потенциальную поверхность скольжения получают, используя векторы полных смещений bi и горизонтальные деформации. [20] Недостатки метода круглоцилиндрической поверхности [40, 46, 64, 81, 98]:

Занижение величин нормальных напряжений в области призмы активного давления;

Завышение величин нормальных напряжений в области призмы упора вследствие не учета реакций между смежными блоками. Это приводит к тому, что коэффициент запаса, рассчитанный методом алгебраического сложения сил, заведомо меньше фактического, а степень этого несоответствия зависит от высоты откоса, его угла и углов внутреннего трения пород и может колебаться от 3 до 20 %.

В состоянии предельного равновесия по принятой поверхности скольжения выполняется равенство моментов удерживающих и сдвигающих сил:

. Таким образом, удовлетворяется равенство нулю моментов, условие же равенства нулю проекций сил на координатные оси не удовлетворяется. Если массив находится в допредельном равновесном состоянии, то, очевидно, что удерживающие силы будут превосходить сдвигающие и коэффициент запаса устойчивости 1. В этом случае не выполняются все три уравнения статики.

Фактическая поверхность скольжения имеет более сложное очертание за счет обязательно имеющегося разброса свойств пород в массиве. Обрушение обычно охватывает не всю длину откоса, а только наиболее ослабленную его часть. Поверхность обрушения в общем случае состоит из цилиндрического участка в активной части и криволинейных поверхностей по краям участка.

Невозможность учета криволинейных отрезков бортов карьера. Учет деформаций строго по профильной линии.

Простое алгебраическое сложение сдвигающих и удерживающих сил, возникающих в основании каждого элементарного блока породы.

Если в массиве откоса нет согласно падающих в сторону карьера поверхностей ослабления, получаем достаточную точность расчета.

При высоте откосов до 100 м и небольших значениях углов трения пород ( 20°) метод дает достаточно надежные результаты.

водонасыщенных горных породах глинистого и песчано-глинистого состава, когда в условиях всестороннего сжатия при определенных величинах напряжений прочностные характеристики данных разностей не могут быть представлены постоянными величинами и С, так как у этих пород сопротивление сдвигу перестает возрастать при росте нормальных напряжений [20, 98].

Для решения объемной задачи устойчивости откосов глубоких карьеров при фиксированной поверхности скольжения используют пространственногеометрический метод. Расчет выполняется в такой последовательности:

Составляют план изомощностей пород оползневого участка.

Оползневой участок разбивают на элементарные блоки, вытянутые по нормали к простиранию откоса или параллельно направлению фронта работ.

участка и поверхности скольжения в блоках выделяют элементарные отсеки, для которых вычисляют удерживающие и сдвигающие силы.

Учитываются величина оползневого давления Е (давление со стороны смежных блоков и отсеков), а также силы трения и сцепления между смежными блоками.

Условие равновесия элементарных блоков рассматривается по отсекам сверху вниз, для чего берется сумма проекций сил на направление возможного смещения в пределах каждого откоса.

Этот метод целесообразно использовать при обратных оползневых расчетах для определения реологических характеристик горных пород.

К плюсам пространственно-геометрического метода можно отнести:

учитывается структурная неоднородность массива;

расчет устойчивости производится по поверхностям ослабления или расчленения любой сложности, реализующимся в поверхности скольжения;

учитываются силы взаимодействия по вертикальным граням смежных объемных элементов;

устойчивость откоса оценивается по величине оползневого давления в его нижней части, т. е. в зоне концентрации сдвигающих напряжений;

возможность выявить изменение состояния бортового массива в процессе ведения горных работ.

При исследовании устойчивости откосов задача заключается в том, чтобы, зная пределы применения расчетных схем и их обоснованность, полнее учитывать инженерно-геологические условия месторождения и технологию горных работ.

[20] В работе [81] выделяют наиболее надежный и универсальный метод расчета устойчивости бортов карьеров и отвалов в реальных горно-геологических условиях. Метод векторного сложения сил, и созданные на его основе ВНИМИ графики по определению предельных параметров устойчивых бортов карьеров, определяют зависимости между высотой плоского откоса Н и его углом для различных углов внутреннего трения и сцепления пород С, по которым можно оценивать устойчивость борта с заданными параметрами и определить максимальные параметры при заданном коэффициенте запаса устойчивости.

Отмечают так же необходимость решения объемной задачи при анализе устойчивости борта в условиях современных темпов и объемов горных работ.

РЕШЕНИЕ ПЛОСКОЙ И ОБЪЕМНОЙ ЗАДАЧИ ПРИ РАСЧЕТЕ

УСТОЙЧИВОСТИ БОРТОВ ОТКОСОВ И ИХ АНАЛИЗ

В настоящее время не существует универсальных методов расчета устойчивости бортов карьеров, учитывающих все влияющие факторы. Выбор зависит от конкретных геологических и горнотехнических факторов, влияющих на устойчивость бортов уступов и откосов. Получение более точных данных, а значит, эффективность метода оценивается путем сравнения недостатков и условий применения каждого из них. На практике механизм разрушения откоса должен изучаться в деталях путем сбора достаточного количества информации и достоверных наблюдений для того, чтобы выбрать наиболее подходящий метод [65, 82, 90, 95, 97].

Решение плоской задачи устойчивости борта используется наиболее часто, ввиду своей простоты [3, 4, 20, 29 – 31, 41, 43, 47]. Однако, подобные методы основываются на упрощенных расчетах, сводящих решение трехмерных проблем до двухмерных, что значительно снижает точность [98].

В реальных условиях следует учитывать и такие факторы как: сложная геометрия карьера и весьма неоднородные свойства горного массива, откосы в некоторых местах перегружены горнотехническими сооружениями и пр. Можно сделать вывод, что, в ряде случаев, игнорирование подобных факторов связано с большими рисками [21, 26, 42, 45]. В данных условиях, без использования трехмерных способов расчета невозможно получить реальную картину напряженно-деформационных свойств пород карьера.

В работе [98] рассмотрен анализ двухмерных и трехмерных методов расчета устойчивости бортов откосов на примере программ PLAXIS 2D и PLAXIS 3D.

В 1 и 2 примере были построены модели горного массива, физикомеханические свойства указаны в таблице 1.2. На основе этого в разных представленные в таблице 1.3. В результате, полученные данные позволяют нам сделать вывод о том, что величина коэффициента запаса устойчивости расчетов, произведенных трехмерным способом, всегда будет выше двухмерного.

Таблица 1.2 – Свойства пород Таблица 1.3 – Коэффициент запаса устойчивости, полученный в разных программах.

Рисунок 1.12 – Деформационная сетка для расчета методом конечных Рисунок 1.13 – Деформационная сетка для расчета методом конечных Рисунок 1.14 – Деформационная сетка для расчета методом конечных Рисунок 1.15 – Деформационная сетка для расчета методом конечных Можно сделать вывод о том, что выбор метода расчета (2D или 3D) имеет большое значение. Увеличение максимальных углов погашения борта карьера возможно и позволит сократить объем вскрышных работ и произвести отработку залежей полезного ископаемого в массиве, сохраняя уровень безопасности на горных работах и улучшая технико-экономические показатели.

МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ ДЛЯ ОЦЕНКИ НАПРЯЖЕННОДЕФОРМИРОВАННОГО СОСТОЯНИЯ ОТКОСОВ КАРЬЕРОВ

Для решения поставленной в данной работе задачи был выбран программный комплекс Plaxis 3D, основанный на методе конечных элементов [2, 94, 96, 100, 101] и способный рассчитать напряжения в сложной трехмерной конструкции в массиве горных пород, учитывая физико-механические свойства.

Решение пространственных задач методом конечных элементов (МКЭ) не имеет принципиальных отличий от двумерной задачи. Изначально затруднения вызывались громоздкостью представления исходных данных и в ряде случаев малой мощностью ЭВМ. Сопоставление плоской задачи теории упругости (при треугольных конечных элементах) с пространственной задачей (при конечных элементах в виде тетраэдров) показывает, что если в плоской задаче среднего объема число неизвестных может быть порядка 300, то в пространственной задаче их количество достигает 5000.

Но с развитием технологий и появлением современных программных комплексов эти трудности исчезли. В последние годы все больше растет перспективность использования способа МКЭ для решения пространственных задач.

В настоящее время МКЭ является самым популярным методом решения дифференциальных уравнений, которыми, как известно, описываются практически все физические явления. По своей сути он является развитием известного и популярного в свое время метода конечных разностей (МКР, метод сеток). Существенное наглядное совершенствование состоит в том, что в МКР осуществлялась регулярная дискретизация области (прямоугольники для двумерных и параллелограммы для трехмерных задач) в МКЭ можно использовать элементы практически любых объемов и форм.

МКЭ посвящено большое количество работ. Из зарубежных можно выделить [94]. Почти одновременно с иностранной литературой по МКЭ выходили в свет разработки отечественных ученых, например [2].

Суть МКЭ состоит в следующем. Используются методы вариационного исчисления. Общей характеристикой – функционалом – в вариационных методах является некая скалярная величина, зависящая от функций как от аргументов. В механике твердого деформированного тела под функционалом понимают полную потенциальную энергию деформированного тела и действующие на него нагрузки. Таким образом, при решении задач МКЭ используется фундаментальный принцип сохранения механической энергии [96, 100].

Рассмотрим некоторое сплошное тело, объем которого равен V, расчлененное на элементы. Пусть в теле и на его границе действуют объемные Q и поверхностные P силы. Уравнение потенциальной энергии данной системы (Э) имеет вид:

перемещениями узлом элементов, но во взаимодействии с компонентами жесткости всей системы. Последнюю можно представить как квадратную матрицу [K] размерностью n = Nт * Nс, где Nт – количество узловых точек, Nс – количество степеней свободы. Тогда выражение для потенциальной энергии деформации примет вид:

Из выражения (1.5) с учетом 1.6 и 1.7 можно получить:

которое и есть основное матричное уравнение МКЭ. Компоненты матрицы жесткости определяются координатами узлов элементов и их упругими характеристиками: модулем упругости и коэффициентом Пуассона. Поэтому достаточным условием является определенность вектора нагрузки или вектора перемещений , либо смешанные, взаимно уравновешивающие условия.

Внешняя ясность и простота МКЭ складываются из довольно непростых задач, если иметь в виду решение практических вопросов. При детальном изучении применения МКЭ выясняется, что даже для относительно легких задач требуется применение вычислительной техники (компьютера) и исследователю при этом необходимо решить ряд технических вопросов, которые могут стать проблемными:

об алгоритме дискретизации области на элементы;

об алгоритме составления, хранения в машинной памяти и решения больших систем уравнений;

об алгоритме ввода исходных данных, управления процессом реализации МКЭ; интерпретации результатов и наглядного их представления.

Первый вопрос связан с решением задач моделирования среды и адекватного ее описания дискретной математической (конечно-элементной) моделью. Для объемных моделей может понадобиться сотни тысяч элементов в виде тетраэдров для описания реальных геологических и горнотехнических условий разработки полезного ископаемого. Такой же порядок размерности естественно будет иметь и система уравнений, получающаяся при раскрытии выражения (1.24). Если не использовать специальные способы формирования и хранения матрицы жесткости системы К (см. 1.23), то даже современным мощным компьютерам не в состоянии обрабатывать квадратную матрицу размером 105 или в 100 Гb (при размере числа 10 b). При эффективной упаковке матрицы встает вопрос о выборе и применении метода решения больших систем уравнений. Эти задачи составляют второй вопрос. Третий вопрос связан с первым и заключается в основном в решении задач программирования.

В зависимости от степени решения этих вопросов можно судить об уровне программных модулей по реализации МКЭ и в целом о возможностях рассматриваемых программных комплексов (ПК). Без использования специальных программ (пре- и постпроцессорных модулей) реализация МКЭ представляет собой рутинное дело. Так, в работах приводится случай, когда одному из ведущих самолетостроительных КБ, при внедрении МКЭ в свою расчетную практику, понадобилось полгода для подготовки исходных данных к расчету крыла самолета, и столько же времени было затрачено на интерпретацию полученных результатов. В то время как сам счет по МКЭ составил считанные минуты.

Одним из первых примеров ПК по реализации МКЭ может служить программа «ASKA», разработанная в начале 1960 г. под руководством проф. Дж.

Аргириса [94]. Программа была составлена для определенного типа ЭВМ.

Большой вклад в развитие МКЭ внесли работы Б.З. Амусина и А.Б. Фадеева [2].

В настоящее время разработано достаточно много программных комплексов (ПК) по реализации МКЭ. В диссертационной работе использовались несколько ПК: Plaxis 3D [100], Phasa [99] и «НЕДРА». Их возможности будут раскрыты по мере использования ниже.

ПРЕИМУЩЕСТВА ИЗУЧЕНИЯ ВЛИЯНИЯ КРИВОЛИНЕЙНОСТИ

НА УСТОЙЧИВОСТЬ БОРТОВ КАРЬЕРОВ

криволинейности позволит значительно облегчить процесс контроля за сдвижением породного массива. Полученная информация не только сократит время и трудозатраты, определив наиболее подходящие места для закладки наблюдательных станций и их ориентацию, но позволит определить периодичность съемки для дальнейшего контроля и даст общее представление о напряженно-деформируемом состоянии уступов карьеров. Понимание процесса деформирования горных пород, его направления является ключевым фактором в обеспечении безопасности на горном предприятии [5, 22, 47, 62, 78, 79, 91].

Одним из явных преимуществ данного исследования является повышение точности определения коэффициента запаса устойчивости откоса. Учет этого параметра традиционным способом не способен обеспечить необходимой точности результатов из-за отсутствия надежных расчетов. С появлением компьютерных программ, способных обрабатывать большой объем информации, включающий геомеханические особенности породного массива, не затрачивая много времени, стало возможным приблизить теоретические и аналитические данные к реальным условиям. Зарекомендовавший себя метод конечных элементов, исполненный в представленных программах, позволит математически обоснованно подойти к решению поставленной задачи.

В процессе отработки при анализе процесса сдвижения часто не учитывают ряд горно-геологических и горнотехнических факторов, влияющих на устойчивость, сводя расчеты к обобщенным параметрам для простоты вычислений. При использовании новой методики ведение горных работ и проектирование выработок станет более обоснованным. Составление общих схем зависимости криволинейности борта от физико-механических свойств пород позволит обеспечить повышение уровня безопасности, определяя геометрические параметры уступа для того или иного случая.

На конечных этапах разработки горизонтов значительная часть рудных запасов остается в бортах и дне карьера, ввиду сложного строения меднорудных месторождений, выражающихся в наличии рудных тел неправильной формы и мелких сопровождающих залежей [81]. Разрабатываемая методика определит участки возможной доработки и поможет обосновать безопасность их выемки.

Все вышесказанное дает основания сделать вывод о том, что решение поставленной задачи в данном исследовании будет реальным вспомогательным рычагом при разработке горных пород открытым способом.

ВЫВОД ПО ПЕРВОЙ ГЛАВЕ

Вопрос определения напряженно-деформированного состояния откоса у карьеров с криволинейными бортами в плане уже поднимался исследователями и был рассмотрен на основе фактических данных и использования метода эквивалентных материалов. В настоящее время разработанная методика оценки устойчивости криволинейных участков бортов широко применяется при проектировании карьеров и оптимизации их форм. Вместе с тем, такой подход не позволяет учесть целый ряд параметров (механических свойств породы, силы бокового распора, геометрию карьера) в широком спектре их значений.

Актуальность данного исследования обоснована существованием реальной производственной проблемы оценки влияния на устойчивость борта его кривизны. Решение ее в определенной степени возможно на основе изучения напряженно-деформированного состояния массива, вмещающего открытую горную выработку. Развитие современных компьютерных программ, способных обрабатывать большие объемы информации, дает возможность приблизить теоретические и аналитические расчеты к реальным условиям благодаря учету геомеханических особенностей исследуемого участка в объемном решении задачи, сократив тем самым время и трудозатраты анализа устойчивости и обеспечив повышение точности контроля устойчивости бортов и безопасности ведения горных работ. Многовариантное моделирование и реализация нелинейной задачи напряженно-деформированного состояния приконтурного породного массива у карьеров с криволинейными бортами в плане, позволит определить поправку в расчетные схемы и, тем самым, обеспечить уточнение геометрических параметров устойчивости бортов карьера.

Таким образом, для решения актуальной задачи оценки устойчивости криволинейного в плане карьера необходимо решить следующие задачи:

провести математическое моделирование деформационного процесса прибортового массива карьера различной формы в плане разработать методику оценки устойчивости борта карьера с учетом его криволинейности провести экспериментальную проверку созданной методики.

СОСТОЯНИЯ БОРТОВ КАРЬЕРОВ КРИВОЛИНЕЙНОЙ ФОРМЫ В

2.1 ОСОБЕННОСТИ ДЕФОРМИРОВАНИЯ ПРИБОРТОВОГО

МАССИВА ГОРНЫХ ПОРОД С РАЗНОЙ КРИВОЛИНЕЙНОСТЬЮ БОРТА

В ПЛАНЕ

Обеспечение безопасности на участке горных работ напрямую зависит от горно-геологических и горнотехнических факторов, влияющих, в свою очередь, на выбор параметров устойчивости борта карьера [13, 24, 72, 83]. В этой связи, знание о влиянии конфигурации борта карьера на деформационный процесс весьма важно, так как позволяет более рационально проектировать горные работы, варьируя параметрами карьера [58, 59, 61]. В частности для карьеров круглой формы в плане (рисунок 2.1) коэффициент запаса устойчивости борта, очевидно, будет выше, чем борт карьера протяженного, прямоугольного в плане, с размерами малой стороны равной диаметру круглого. При этом, безусловно, рассматриваются равные величины углов откоса карьеров и его высота.

К геометрическим составляющим относятся: форма карьера в плане, глубина, длина, ширина, радиус (и их соотношения), а также угол борта карьера.

К физико-механическим параметрам при решении объемной упругой задачи основным параметром будет модуль упругости пород, а при использовании плоской нелинейной задачи – входные параметры для модели Кулона-Мора (объемный вес пород, сцепление и угол внутреннего трения) [100].

Для оценки напряженно-деформированного состояния прибортового массива в объемном виде принят программный комплекс Plaxis 3D. Данная программа позволяет математически обоснованно подойти к решению поставленной объемной задачи, учесть свойства слагающих пород и представить смещения массива.

Использовались упрощенные модели карьеров, сформированные в однородном массиве горных пород (в данном случае сложенными из аргиллитов и алевролитов). Значения механических характеристик приняты усредненными в следующих пределах: модуль упругости 1 – 10 ГПа, коэффициент Пуассона 0,25Формы карьеров в плане показаны на рис. 15. Высота результирующего уступа принята, равной 300 метрам. [61] Рисунок 2.1 – Рассматриваемые формы карьеров в плане По результатам моделирования (рисунок 2.2) наблюдаем весьма существенную разницу в общих смещениях пород в приконтурном массиве. Так, при рассмотрении вытянутого (прямоугольного карьера) – зона наиболее интенсивных смещений (красный и желтый цвет) располагается в срединной части и распространяется существенно дальше от борта карьера, чем это наблюдается в приконтурных частях круглого и квадратного в плане карьеров в условиях однородного массива. По внутренним углам бортов карьера, напротив, наблюдаем существенное уменьшение общих смещений.

Рисунок 2.2 – Модели карьеров разной криволинейности в плане Не рассматривая эффекты, связанные с разнообразием геологического геометрическими параметрами карьеров. Например, при изучении протяженного карьера с неровной границей в плане, места, где наблюдается вогнутость линии борта (фокус нормалей к борту карьера ориентированы в сторону выработанного пространства) будут испытывать меньшие горизонтальные смещения и соответственно будут более устойчивы. В этих зонах реализуется так называемый «арочный эффект», при котором происходит зажим пород, что препятствует их деформированию в выработанное пространство.

ориентированы в сторону прибортового массива) будут обладать наименьшей устойчивостью.

Вместе с тем, следует отметить, что при выборе схемы вскрытия месторождения, способа разработки и, как следствие, его окончательной формы в плане необходимо учитывать горно-технические и горно-геологические особенности месторождения с обеспечением устойчивости рабочих и нерабочих бортов [41, 46, 47, 51, 67, 90, 97], предусматривая в проектах соответствующие мероприятия по предотвращению деформаций откосов [33, 66].

Для решения поставленной задачи необходимо определить «поведение»

массива при разной геометрии выработанного пространства. Анализировались модели карьеров, сформированные в однородном массиве аргиллитов. Формы карьеров варьировались при различных углах результирующего откоса и глубине разработки [60].

Анализ горизонтальный смещений прибортового массива производился по схеме, представленной на рисунке 2.3, где L1 – длина стороны, по которой определяются горизонтальные смещения, L2 – длина стороны, перпендикулярная данной, глубина Н соответствовала рабочему спектру глубин существующих карьеров и принималась равной 100, 300 и 500 метрам. Показатели смещений породного массива определялись по подошве откоса, где величины напряжений достигают наибольших значений. Полученные значения сравнивались с аналогичными для карьера круглой формы в плане с диаметром D равным L1 и глубинами H.

Рисунок 2.3 – Схема для определения горизонтальных смещений у карьеров с разной конфигурацией в плане (а – обозначение сторон прямоугольного в плане карьера, где L1 –определяемая сторона, L2 – сторона перпендикулярная L1; б – сечение по линии определяемых горизонтальных смещений) Образование выемки (рисунок 2.3, а) в результате отработки эквивалентно снятию нагрузки по контуру «чаши карьера», в результате чего перемещения, в рассматриваемой нами области получили направление вверх и к центру за счет упругого восстановления массива [2].

На основе результатов моделирования были найдены зависимости, характеризующие величину смещений у карьеров с разными геометрическими параметрами, представленные на рисунках 2.4, 2.5, 2.6. Ось абсцисса характеризуется отношением L1 к L2, ординат – величина горизонтальных деформаций в метрах. Кривые графиков, на каждой из рассмотренных глубин разработки, отражают смещения массива при разном значении L2.

смещения Рисунок 2.4 – График смещений для глубины разработки 100 метров смещения Рисунок 2.5 – График смещений для глубины разработки 300 метров смещения Рисунок 2.6 – График смещений для глубины разработки 500 метров Полученные зависимости отражают весьма существенную разницу в сопротивления смещению в потенциальной призме обрушения, создаваемого силами бокового распора в зонах с разной кривизной. Так, при анализе вытянутого (прямоугольного) карьера с увеличением рассматриваемой стороны заметно увеличиваются и смещения. По выявленным данным видно, что при L1/H3 не зависимо от величины L2 эффект «зажима» горного массива перестает действовать и показатели смещений перестают расти. Существование этой условной границы подтверждается и в ряде работ ВНИМИ, Унипромеди и СГИ [33, 66, 81]. Действующие методики оценки устойчивости бортов устанавливают это значение равным 2 [44], однако, в более поздних работах оно увеличивается до 3 [81]. Эта особенность объясняется тем, что более ранние методики исследования, значительно уступали по возможностям современным. Имеется много прямых и косвенных математических расчетов показывающих, что на удалении порядка 3 размеров от условного двумерного в сторону третьего измерения, например, торцевая часть выработки, ее влияние становится не существенным.

Зависимости, представленные на графиках, могут быть описаны следующим образом [60]:

Определяем горизонтальные смещения по подошве откоса (рисунок 2.3) в плоскости перпендикулярной L1H по формуле:

где L1 – длина стороны, по которой определяются горизонтальные смещения, L2 – длина стороны, перпендикулярная данной, Н – глубина Учтем эффект зажима, определяемого величиной стороны L2 в плоскости L2H, введем поправку в рассчитанные зависимости:

При сравнении величин смещений для карьеров круглой формы в плане с диаметром равным большей стороне прямоугольного карьера, получаем меньшие значения за счет бокового зажима. Но при D/H3 значения горизонтальных смещений круглого карьера становиться аналогичным вытянутому, показатель устойчивости в таком случае может быть рассчитан способом, применимым для прямолинейного борта (рисунок 2.7).

Рисунок 2.7 – График смещений для круглого карьера диаметра D при деформационный процесс в массиве горных пород, является форма карьера в плане и глубина разработки. На основе этого факта установлена зависимость влияния показателя криволинейности борта карьера на возникающие смещения.

Однако, для получения обобщенной картины напряженно-деформируемого состояния борта следует учесть влияние физико-механических свойств пород, которые для общего случая можно моделировать вариацией упругих параметров.

МОДЕЛИРОВАНИЕ ДЕФОРМАЦИЙ БОРТА КАРЬЕРА С РАЗНЫМИ

СВОЙСТВАМИ ГОРНЫХ ПОРОД И ГЕОМЕТРИЕЙ В ПЛАНЕ

Как отмечалось ранее степень действия сил бокового распора, возникающих за счет дополнительного сопротивления смещения призмы обрушения, зависит помимо особенностей инженерно-геологических факторов прибортового массива также от конфигурации борта в плане, и соотношения протяженности откоса и его высоты [10, 33, 66, 81, 100].

Выявление зависимостей геометрических параметров при учете свойств пород позволят определить геомеханическую составляющую деформационного процесса и оценивать разные участки борта карьера (вогнутые, а также находящиеся у мест с резким изменением конфигурации карьера в плане) по степени устойчивости, что представляется важным при проектировании и планировании горных работ [58].

Анализ горизонтальных смещений прибортового массива производился по схеме (рисунок 2.3), глубина Н принималась равная 100, 300 и 500 метрам.

Величина модуля деформации Е для разных групп моделей определялась величинами 30Мпа, 1Гпа и 30 Гпа. Оценивались горизонтальные смещения пород у нижней бровки карьера, где величины напряжений достигают наибольших значений.

На основе результатов моделирования были найдены зависимости, характеризующие величину смещений у карьеров с разными геометрическими и прочностными характеристиками, представленные на рисунках 2.8, 2.9, 2.10.

Рисунок 2.8 – График смещений для глубины разработки 100 метров Рисунок 2.9 – График смещений для глубины разработки 300 метров Рисунок 2.10 – График смещений для глубины разработки 500 метров По представленным графикам явно прослеживается тенденция увеличения смещения при возрастающем отношении L1/L2, что подтверждает ранее полученные результаты. Кроме того, при разных показателях модуля деформации E получаем естественное изменение в показателях величин смещений по подошве откоса, но конфигурация кривых графика как бы повторяется. Это значит, что распределение смещений при изменении геометрии карьера будет схожим при разной механике горных пород и может быть описано общим законом.

Подтверждается и тот факт, что при L1/H3 не зависимо от величины L2 и значений прочностных показателей эффект «зажима» перестает действовать и показатели смещений перестают расти. Обратим внимание, что данное граничное условие действия сил бокового распора, при котором решение объемной задачи сводится к плоской, характерно для всех форм карьеров в плане. Это, несомненно, важное условие позволяет определить «точку отсчета» для дальнейших исследований. Значение коэффициента запаса устойчивости борта в условиях изотропного массива, в случае L1/H=3, следует условно принять равным 1. При этом, последующее возрастание или убывание величины коэффициента устойчивости (в следствии, например, разбортовки карьера или увеличения глубины разработки) будет наглядно отображаться в изменении принятого условного значения.

рассматриваемого борта, геометрические параметры которого отвечают условию L1/H3, целесообразно определять по отношению горизонтальных смещений плоского борта (L1/H=3) к смещениям определяемого. Найденный коэффициент запаса устойчивости с учетом объемного фактора характеризует повышение устойчивости «зажатого» участка откоса. Этот факт закладывает определенный запас в обеспечении устойчивости борта карьера и позволяет оптимизировать геометрические параметры.

Для выражения деформационного процесса в виде коэффициента в известных формулах расчета устойчивости бортов карьера определим зависимость величин прочностных характеристик массива горных пород от геометрических показателей карьера.

Исследования изменчивости показателя сцепления производились в плоскости борта карьера перпендикулярно фронту работ, при которых соблюдается устойчивость выработок с разными углами и высотой откоса. В дальнейшем эти данные послужат разработке методики, определяющей отличие условий устойчивости борта карьера в зонах с разной кривизной [59].

Для определения поправки использовано нелинейное моделирование для плоской задачи в программе Phase (рисунок 2.11, 2.12). При построении так же пользовались схемой упрощенной модели бортов карьера из однородного массива пород.

Величина модуля деформации Е определялась величинами 30Мпа, 1Гпа и 30 Гпа.

Показатель сцепления пород подбирался так, чтобы во всех случаях коэффициент запаса устойчивости был одинаков (n= 1.2).

Рисунок 2.11 – Дискретизация модели уступа с углом откоса = Рисунок 2.12 – Интерпретация расчета уступа при фиксированном коэффициенте На основе результатов моделирования были найдены зависимости, характеризующие изменчивость показателя сцепления горных пород при разных углах отработки, представленные на рисунках 2.13, 2.14, 2.15.

Полученные результаты позволяют определить поправочные величины в расчетное значение коэффициента запаса устойчивости для прямолинейного борта. Зоны борта карьера, находящиеся в условиях так называемого зажима пород (например, в местах вогнутости или углах карьера) будут иметь повышенный коэффициент устойчивости, однако, зависимость показателя сцепления от меняющейся геометрии уступа будет аналогичной [52, 64, 65, 82, 95].

РАСЧЕТ ПОПРАВОЧНЫХ КОЭФФИЦИЕНТОВ ЗА ВЕЛИЧИНУ

УГЛА ОТКОСА БОРТА КАРЬЕРА

Для удобства и с целью определения коэффициента, описывающего изменчивость показателя сцепления, по имеющимся данным был построен график зависимости показателя сцепления от величины результирующего откоса уступа (отношения высоты уступа на синус его угла H/sin). Результаты представлены на рисунке 2.16.

Рисунок 2.16 – График изменчивости сцепления при E=1 ГПа Полученный масштабный коэффициент при разном значении Н (100, 300, 500) равен 1. Таким образом, изменчивость сцепления можно описать формулой [60]:

Данный показатель является поправочным коэффициентом в прочностные характеристики расчетной схемы устойчивости уступа для решения в плоской постановке задачи.

РАСЧЕТ ПОПРАВОЧНОГО КОЭФФИЦИЕНТА СЦЕПЛЕНИЯ

Анализ геометрии карьера позволил определить коэффициент зажима 2, характеризующий величину смещений у карьеров с разной формой в плане и глубиной разработки. Результаты расчетов устойчивости дадут возможность определить поправку в расчетную схему коэффициента запаса устойчивости [58 По выводам, сделанным ранее, определим показатель устойчивого состояния откоса равным 1 при соотношении L1/H=3. Проведя анализ смещений при разном соотношении L1/L2,получим наглядное изменение устойчивости.

характеристики коэффициента запаса устойчивости были проанализированы ряд моделей, разработанных в программе Phase. Глубина разработки H принималась 100, 300 и 500 метров. Угол откоса принимался постоянным. Модуль деформации Е=1 ГПа, удельный вес =2т/м3, угол внутреннего трения =30. Показатель сцепления в массиве откоса увеличивался до значения, перерасчет в коэффициент запаса устойчивости которого удовлетворял соответствующему значению показателя устойчивости для разных соотношений L1/L2 для прямоугольного карьера (рисунок 2.4, 2.5, 2.6) и диаметра D – для круглого (рисунок 2.7). Все это позволило определить изменение прочностной характеристики породного массива от геометрии карьера в плане при постоянном значении физикомеханических свойств и угла откоса.

Данные, полученные описанным образом, представлены на графике зависимости поправки в величину сцепления пород от горизонтальных смещений 2 (рисунок 2.17).

Рисунок 2.17 – График зависимости поправки в величину сцепления пород Поправка в расчетную схему коэффициента запаса устойчивости откоса может быть описана формулой:

где 2 – горизонтальные смещения по подошве откоса, Н – глубина карьера.

Анализ полученных моделей позволяет получить график зависимости объемного коэффициента устойчивости от поправки в величину сцепления (рисунок 2.18).

Рисунок 2.18 – График зависимости объемного коэффициента устойчивости Расчет поправочного коэффициента в показатель сцепления в данном случае будет представлен формулой:

где n – объемный коэффициент устойчивости, Н – глубина карьера.

либо в общем случае:

породы С, L – длина дуги численно равная площади поверхности скольжения цилиндрического тела.

Отметим, что объемный коэффициент запаса устойчивости, полученный применением поправки y легко проверить сравнением полученного результата со значением показателя устойчивости, найденного отношением горизонтальных смещений плоского борта (L1/H=3) к смещениям определяемого при L1/H3.

ОПРЕДЕЛЕНИЕ ДОБАВОЧНОГО УГЛА В ГЕОМЕТРИЧЕСКИЕ

ПАРАМЕТРЫ ОТКОСА

В разработанных методиках результирующий угол откоса рассчитывается как сумма угла наклона прямолинейного в плане борта плоского профиля и поправки к этому углу за кривизну борта в плане [33, 66, 81, 86, 87].

Для определения поправки в угол откоса использовано нелинейное моделирование в программе Phase, рассмотрены модели борта карьера высотой откоса от 100 до 500 метров с углом откоса, обеспечивающим получение значения коэффициента запаса устойчивости равным 1 (рисунок 2.19). Затем, вводя поправку в прочностные характеристики, повышали коэффициент до значения с учетом действия сил бокового распора 2 для прямоугольного (рисунок 2.4, 2.5, 2.6) и для круглого карьера (рисунок 2.7). Увеличивая угол наклона борта, добивались получения первоначальной величины коэффициента запаса устойчивости равным 1. Подобные действия были проведены для всех соотношений бортов карьеров, отвечающим условию L/H3.

На рисунке 2.19 приведен пример построения результирующего борта карьера с глубиной разработки Н=300 метров, модулем деформации Е=1 ГПа, плотностью пород =2 кН/м3, углом внутреннего трения = 30, показателем сцепления С=22 т/м2 и углом откоса =50. Эффект от соотношения приведенных показателей борта выражается в получении коэффициента запаса устойчивости, равного 1. Изменив величину значения сцепления пород до 37 т/м 2 добиваемся увеличения показателя устойчивости до значения 1.25, что соответствует значению, для L1 и L2 равным 500 метрам. Увеличив значение угла откоса, приводим показатель коэффициента запаса устойчивости к первоначальному значению равному 1. На рисунке 2.20 показано напряженно-деформируемое состояние уступа с учетом объемного коэффициента запаса устойчивости.

Рисунок 2.19 – Изменение угла откоса уступа с учетом объемного Рисунок 2.20 – Построение модели уступа с заданным коэффициентом устойчивости равным 1 (а – дискретизация рабочей области с заданными геометрическими параметрами, б – интерпретация результатов расчета).

Таким образом, использовано плоское решение задачи об устойчивости борта, в котором были введены поправки, полученные на основе объемной задачи для учета криволинейности борта карьера в плане. Проведя анализ по предложенной схеме, получаем добавочные величины углов с учетом степени влияния удерживающих сил (рисунок 2.21).

Рисунок 2.21 – График определения поправки к углу откоса при разной Поправочный коэффициент к углу откоса борта описывается формулой:

где n – величина объемного коэффициента запаса устойчивости.

Общий угол откоса, в этом случае, рассчитывается как сумма угла наклона прямолинейного в плане борта плоского профиля, вычисленного по графикам ВНИМИ [33, 66], и поправки к этому углу:

Пунктирная линия на рисунке 2.21 отражает максимальные величины, которые определяются по действующим нормативным методикам. Как уже упоминалось эти методики эмпирические и не рассматривают всего спектра возможных условий. Понятно, что и приведенные величины, превышающие также пока не обоснованы надежно. В этой связи, применение добавочных углов более 25 в реальных условиях требует более глубоких исследований.

УЧЕТ КРИВОЛИНЕЙНОСТИ ЛОКАЛЬНЫХ УЧАСТКОВ

В практике ведения горных работ при открытом способе разработке месторождений полезных ископаемых зачастую борт карьера имеет вогнутые и выпуклые участки. Эти участки обладают отличными геомеханическими условиями, относительно прямолинейных.

В программе Plaxis 3D производилась оценка горизонтальных смещений по нижней бровке откоса у бортов карьеров с разным углом поворота в плане (рисунок 2.22). Поворот выработки моделировался от 45 до 180.Оценивались внутренние и внешние углы. В первом случае показатель деформации будет значительно ниже из-за возникающих сил бокового распора, соответственно устойчивость будет выше.

Рисунок 2.23 – График зависимости поправки к коэффициенту устойчивости от Поправочный коэффициент криволинейности локальных участков борта выражается формулой:

, где n – объемный коэффициент устойчивости уступа, t – изменение горизонтальных смещений при разном.

Источник

Устойчивость бортов карьера. Факторы, влияющие на устойчивость бортов.

Что относится к основным факторам которые учитываются при оценке устойчивости бортов

УТВЕРЖДЕНприказом Федеральной службыпо экологическому, технологическомуи атомному надзоруот 13 ноября 2020 года N 439

I. Область применения

II. Факторы, влияющие на устойчивость бортов, уступов карьеров, разрезов и откосов отвалов

III. Требования к инженерно-геологическому изучению и районированию массива горных пород

«НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ «ГОРНЫЙ»

МАРКШЕЙДЕРСКАЯ ОЦЕНКА УСТОЙЧИВОСТИ КРИВОЛИНЕЙНОГО

В ПЛАНЕ БОРТА КАРЬЕРА

ДИССЕРТАЦИЯ

ОГЛАВЛЕНИЕ

СОСТОЯНИЯ БОРТОВ КАРЬЕРОВ КРИВОЛИНЕЙНОЙ ФОРМЫ В ПЛАНЕ..

ГЛАВА 3 РАЗРАБОТКА МЕТОДИКИ РАСЧЕТА ПАРАМЕТРОВ

ГЛАВА 4 АПРОБАЦИЯ РАЗРАБОТАННОЙ МЕТОДИКИ НА ПРИМЕРЕ

ВВЕДЕНИЕ

ГЛАВА 1 СОСТОЯНИЕ ИЗУЧЕННОСТИ ВОПРОСА

АНАЛИЗ ИССЛЕДОВАНИЙ В ОБЛАСТИ УСТОЙЧИВОСТИ

БОРТОВ КАРЬЕРОВ

РЕГЛАМЕНТИРУЮЩИЕ ОЦЕНКУ УСТОЙЧИВОСТИ БОРТА КАРЬЕРА

1.1.2 НАУЧНО-МЕТОДИЧЕСКИЕ ЛИТЕРАТУРНЫЕ ИСТОЧНИКИ

1.2 ПРЕДПОСЫЛКИ К РАЗРАБОТКЕ МЕТОДИКИ ПО УЧЕТУ

КРИВОЛИНЕЙНОСТИ БОРТОВ В ОПРЕДЕЛЕНИИ УСТОЙЧИВОСТИ

1.2.1 СУЩЕСТВУЮЩАЯ МЕТОДИКА УЧЕТА КРИВОЛИНЕЙНОСТИ

1.2.2 ИСПОЛЬЗОВАНИЕ МЕТОДОВ РАСЧЕТА ДЕФОРМИРОВАННОГО

СОСТОЯНИЯ МАССИВА ГОРНЫХ ПОРОД ДЛЯ ОЦЕНКИ

УСТОЙЧИВОСТИ БОРТА КАРЬЕРА

РЕШЕНИЕ ПЛОСКОЙ И ОБЪЕМНОЙ ЗАДАЧИ ПРИ РАСЧЕТЕ

УСТОЙЧИВОСТИ БОРТОВ ОТКОСОВ И ИХ АНАЛИЗ

МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ ДЛЯ ОЦЕНКИ НАПРЯЖЕННОДЕФОРМИРОВАННОГО СОСТОЯНИЯ ОТКОСОВ КАРЬЕРОВ

ПРЕИМУЩЕСТВА ИЗУЧЕНИЯ ВЛИЯНИЯ КРИВОЛИНЕЙНОСТИ

НА УСТОЙЧИВОСТЬ БОРТОВ КАРЬЕРОВ

ВЫВОД ПО ПЕРВОЙ ГЛАВЕ

СОСТОЯНИЯ БОРТОВ КАРЬЕРОВ КРИВОЛИНЕЙНОЙ ФОРМЫ В

2.1 ОСОБЕННОСТИ ДЕФОРМИРОВАНИЯ ПРИБОРТОВОГО

МАССИВА ГОРНЫХ ПОРОД С РАЗНОЙ КРИВОЛИНЕЙНОСТЬЮ БОРТА

В ПЛАНЕ

МОДЕЛИРОВАНИЕ ДЕФОРМАЦИЙ БОРТА КАРЬЕРА С РАЗНЫМИ

СВОЙСТВАМИ ГОРНЫХ ПОРОД И ГЕОМЕТРИЕЙ В ПЛАНЕ

РАСЧЕТ ПОПРАВОЧНЫХ КОЭФФИЦИЕНТОВ ЗА ВЕЛИЧИНУ

УГЛА ОТКОСА БОРТА КАРЬЕРА

РАСЧЕТ ПОПРАВОЧНОГО КОЭФФИЦИЕНТА СЦЕПЛЕНИЯ

ОПРЕДЕЛЕНИЕ ДОБАВОЧНОГО УГЛА В ГЕОМЕТРИЧЕСКИЕ

ПАРАМЕТРЫ ОТКОСА

УЧЕТ КРИВОЛИНЕЙНОСТИ ЛОКАЛЬНЫХ УЧАСТКОВ

Вам также понравится

Как вернуться в свой сон

Что можно сделать с пюпитром

Что значит начислить ндс

Добавить комментарий Отменить ответ

УТВЕРЖДЕН
приказом Федеральной службы
по экологическому, технологическому
и атомному надзору
от 13 ноября 2020 года N 439