Что относится к моделям временных рядов
Основные виды эконометрических моделей



Выделяют три основных класса эконометрических моделей. 1. Модель временных рядов.
Модель представляет собой зависимость результативного признака от переменной времени или переменных, относящихся к другим моментам времени.
К моделям временных рядов, в которых результативный призn нак зависит от времени, относятся:
1) модель тренда (модель зависимости результативного признаn ка от трендовой компоненты);
2) модель сезонности (модель зависимости результативного признака от сезонной компоненты);
3) модель тренда и сезонности.
К моделям временных рядов, в которых результативный призn нак зависит от переменных, датированных другими моментами времени, относятся:
1) модели с распределенным лагом, которые объясняют ваn риацию результативного признака в зависимости от предыдуn щих значений факторных переменных;
2) модели авторегрессии, которые объясняют вариацию реn зультативного признака в зависимости от предыдущих значеn ний результативных переменных;
3) модели ожидания, объясняющие вариацию результативноn го признака в зависимости от будущих значений факторных или результативных переменных.
Модели временных рядов делятся на модели, построенные по стационарным и нестационарным временным рядам.
Стационарные временные ряды характеризуются постоянныn ми во времени средней, дисперсией и автокорреляцией, т. е. данn ный временной ряд не содержит трендового и сезонного компоn нента.
Если временной ряд не отвечает перечисленным условиям, то он является нестационарным (т. е. содержит трендовую и сезонn ную компоненты).
2. Регрессионные модели с одним уравнением.
| ( |
| b |
| b |
| ) |
| k |
| 1 k |
y= f (x, )= f x1, ј, xn, 1, ј, b, где b, ј, b — параметры регрессионного уравнения.
Регрессионные модели делятся на парные (с одним факторn
ным признаком) и множественные регрессии.
В зависимости от вида функции f(x, b) модели делятся на лиn нейные и нелинейные регрессии.
3. Системы одновременных уравнений.
Данные модели описываются системами взаимозависимых регрессионных уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых может включать в себя не только факторные переменные, но и результативные перn еменные из других уравнений системы.
Для тождеств характерно то, что их вид и значения параметров известны.
Регрессионные уравнения, из которых состоит система, назыn ваются поведенческими уравнениями. В поведенческих уравнеn ниях значения параметров являются неизвестными и подлежат оцениванию.
Примером системы одновременных уравнений может служить модель спроса и предложения, включающая три уравнения:
| 1 t t |
QSt=a0+a ´P +a2´P−1 —уравнениепредложения;
| 0 1 t 2 |
Qdt=b +b ´P +b ´It —уравнение спроса;
QSt=Qdt —тождество равновесия,
где QSt— предложение товара в момент времени t; Qdt— спрос на товар в момент времени t;
Модели временных рядов. Аддитивная и мультипликативная модель
Модели, которые построенны по данным, характеризующим один объект за ряд определенных последовательных периодов, называется моделями временных рядов.
Временной ряд – это совокупность значений определенного показателя за несколько последовательных периодов времени.
Каждый уровень временного ряда может формироваться из трендовой (Т), циклической или сезонной компоненты (S), а также случайной (E) компоненты.
Модели, где временной ряд представлен в виде суммы перечисленных компонентов называются аддитивными, если в виде произведения – мультипликативными моделями.
Аддитивная модель имеет вид: Y = T + S + E
Мультипликативная модель имеет вид: Y = T * S * E
Построение модели временного ряда
Аналитическое выравнивание временного ряда
Построение аналитической функции при моделировании тренда, в любой задаче по эконометрике на временные ряды, называют аналитическим выравниванием временного ряда и в основном применяются функции: линейную, степенную, гиперболичческую, параболическую и т.д.
Параметры тренда определяются как и в случае линейной регрессии методом МНК, где в качестве независимой переменной выступает время, а в качестве зависимой переменной – уровни временного ряда. Критерием отбора наилучшей формы тренда служит наибольшее значение коэффициента детерминации, критерии фишера и Стьюдента.
Автокорреляция в остатках – корреляционная зависимость между значениями остатков за текущий и предыдущие моменты времени. Для определения автокорреляции остатков используется критерий Дарбина – Уотсона:
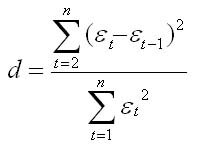
Виды эконометрических моделей
Главным инструментом эконометрического исследования является модель. Выделяют три основных класса эконометрических моделей:
Моделью временных рядов называется зависимость результативной переменной от переменной времени или переменных, относящихся к другим моментам времени.
К моделям временных рядов, характеризующих зависимость результативной переменной от времени, относятся:
а) модель зависимости результативной переменной от трендовой компоненты или модель тренда;
б) модель зависимости результативной переменной от сезонной компоненты или модель сезонности;
в) модель зависимости результативной переменной от трендовой и сезонной компонент или модель тренда и сезонности.
К моделям временных рядов, характеризующих зависимость результативной переменной от переменных, датированных другими моментами времени, относятся:
а) модели с распределённым лагом, объясняющие вариацию результативной переменной в зависимости от предыдущих значений факторных переменных;
б) модели авторегрессии, объясняющие вариацию результативной переменной в зависимости от предыдущих значений результативных переменных;
в) модели ожидания, объясняющие вариацию результативной переменной в зависимости от будущих значений факторных или результативных переменных.
Кроме рассмотренной классификации, модели временных рядов делятся на модели, построенные по стационарным и нестационарным временным рядам.
Стационарным временным рядом называется временной ряд, который характеризуется постоянными во времени средней, дисперсией и автокорреляцией, т. е. данный временной ряд не содержит трендовой и сезонной компонент.
Нестационарным временным рядом называется временной ряд, который содержит трендовую и сезонную компоненты.
Определение. Моделью регрессии с одним уравнением называется зависимость результативной переменной, обозначаемой как у, от факторных (независимых) переменных, обозначаемых как х1,х2,…,хn. Данную зависимость можно представить в виде функции регрессии или модели регрессии:
где β1…βk – параметры модели регрессии.
Можно выделить две основных классификации моделей регрессии::
а) классификация моделей регрессии на парные и множественные регрессии в зависимости от числа факторных переменных;
б) классификация моделей регрессии на линейные и нелинейные регрессии в зависимости от вида функции f(x,β).
В качестве примеров моделей регрессии с одним уравнением можно привести следующие модели:
а) производственная функция вида Q=f(L,K), выражающая зависимость объёма производства определённого товара (Q) от производственных факторов – от затрат капитала (К) и затрат труда (L);
б) функция цены Р=f(Q,Pk), характеризующая зависимость цены определённого товара (Р) от объема поставки (Q) и от цен конкурирующих товаров (Pk);
в) функция спроса Qd=f(P,Pk,I), характеризующая зависимость величины спроса на определённый товар (Р) от цены данного товара (Р), от цен товаров-конкурентов (Pk) и от реальных доходов потребителей (I).
Системой одновременных уравнений называется модель, которая описывается системами взаимозависимых регрессионных уравнений.
Системы одновременных уравнений могут включать в себя тождества и регрессионные уравнения, в каждое из которых могут входить не только факторные переменные, но и результативные переменные из других уравнений системы.
Регрессионные уравнения, входящие в систему одновременных уравнений, называются поведенческими уравнениями. В поведенческих уравнениях значения параметров являются неизвестными и подлежат оцениванию.
Основное отличие тождеств от регрессионных уравнений заключается в том, что их вид и значения параметров известны заранее.
Примером системы одновременных уравнений является модель спроса и предложения, в которую входит три уравнения:
а) уравнение предложения: =а0+а1*Рt+a2*Pt-1;
б) уравнение спроса: =b0+b1* Рt+b2*It;
в) тождество равновесия: QSt = Qdt,
где QSt – предложение товара в момент времени t;
Qdt – спрос на товар в момент времени t;
Рt – цена товара в момент времени t;
Pt-1 – цена товара в предшествующий момент времени (t-1);
It– доход потребителей в момент времени.
В модели спроса и предложения выражаются две результативные переменные:
а) Qt– объём спроса, равный объёму предложения в момент времени t;
б) Pt– цена товара в момент времени t.
Модели временных рядов
Понятие и сущность временных рядов. Нестационарные временные ряды: модели тренда, сезонности, аддитивная, мультипликативная. Методы анализа временных рядов, анализ автокорреляционной функции и коррелограммы. Адаптивные методы прогнозирования показателей.
| Рубрика | Экономико-математическое моделирование |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 31.07.2012 |
| Размер файла | 350,4 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Размещено на http://www.allbest.ru/
по дисциплине: Эконометрика
на тему: Модели временных рядов
1. Понятие и сущность временных рядов
2. Модели нестационарных временных рядов
3. Анализ временных рядов
4. Модели стационарных временных рядов
В настоящее время статистические методы прогнозирования заняли видное место в экономической практике. Широкому внедрению методов анализа и прогнозирования данных способствовало появление персональных компьютеров. Распространение статистических программных пакетов позволило сделать доступными и наглядными многие методы обработки данных.
Все шире используются статистические методы прогнозирования в деятельности плановых, аналитических, маркетинговых отделов производственных предприятий и объединений, торговых, страховых компаний, банков, правительственных учреждений.
Наука, которая на базе статистических данных дает количественную характеристику взаимосвязанным экономическим явлениям и процессам, называется Эконометрикой [7, с 3].
Основная задача эконометрики состоит в построении моделей специфического типа (эконометрических моделей), описывающих взаимообусловленное развитие социально-экономических процессов, на основе информации, отражающей распределение их уровней во времени или (и) в пространстве однородных объектов.
Эти модели используются в анализе и прогнозировании общих закономерностей и конкретных количественных характеристик рассматриваемых процессов, определении управляющих воздействий.
Выделяют три основных класса экономических моделей: модель временных рядов, регрессивные модели с одним уравнением, системы одновременных уравнений.
При построении эконометрической модели используются два типа данных:
1) данные, характеризующие совокупность различных объектов в определенный момент времени;
2) данные, характеризующие один объект за ряд последовательных моментов времени.
Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные на основе второго типа данных, называются моделями временных рядов.
К моделям временных рядов, в которых результативный признак зависит от времени, относятся:
· Модель тренда (модель зависимости результативного признака от трендовой компоненты);
· Модель сезонности (модель зависимости результативного признака от сезонной компоненты);
· Модель тренда и сезонности.
К моделям временных рядов, в которых результативный признак зависит от переменных, датированных другими моментами времени, относятся:
· Модели с распределенным лагом, которые объясняют вариацию результативного признака в зависимости от предыдущих значений факторных переменных;
· Модели авторегрессии, которые объясняют вариацию результативного признака в зависимости от предыдущих значений результативных переменных;
· Модели ожидания, объясняющие вариацию результативного признака в зависимости от будущих значений факторных и результативных переменных.
Модели временных рядов делятся на модели, построенные по стационарным и нестационарным временным рядам.
Стационарные временные ряды характеризуются постоянными во времени средней, дисперсией и автокорреляцией, т.е данный временный ряд не содержит трендового и сезонного компонента.
Если временный ряд не отвечает перечисленным условиям, то он является нестационарным (т.е. содержит трендовую и сезонную компоненты) [7, с 3].
Сезонная компонента отражает повторяемость экономических процессов в течение не очень длительного периода (года, иногда месяца, недели и т.д., например, объем продаж товаров или перевозок пассажиров в различные времена года) [1, с 134] (рис.2)
Очевидно, что реальные данные не следуют целиком и полностью из каких-либо описанных выше моделей. Чаще всего они содержат еще и циклическую и случайную компоненту.
Циклическая компонента отражает повторяемость экономических процессов в течении длительных периодов (например, влияние волн экономической активности Кондратьева, демографических «ям» и т.п.)
Случайная компонента отражает влияние не поддающихся учету и регистрации случайных факторов, делится на 2 вида: факторы резкого, внезапного действия (например, стихийные бедствия, эпидемии и т.п.) и текущие факторы (рис.3).
в табл.1 приведены данные, отражающие спрос на некоторый товар за восьмилетний период (усл.ед.), т.е. временный ряд спроса yt (уровень ряда).
В общем виде при исследовании экономического временного ряда yt выделяется несколько составляющих:
Построим график (рис. 4). Из графика видно, что данная модель имеет тренд, сезонную, циклическую и случайную компоненту.
Аддитивная модель временного ряда это модель, в которой временный ряд представлен как сумма перечисленных компонент.
Мультипликативная модель временного ряда это модель, в которой временный ряд представлен как произведение перечисленных компонент.
Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний.
Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов.
Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
Построение аддитивной и мультипликативной моделей сводится к расчету значений ut vt ?t для каждого уровня временного ряда.
Процесс построения модели временного ряда включает в себя следующие шаги.
1. Выравнивание исходного ряда методом скользящей средней.
2. Расчет значений сезонной компоненты vt.
3. Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных (ut + ?t) в аддитивной или (ut · ?t) мультипликативной модели.
6. Расчет абсолютных и относительных ошибок.
3. Анализ временных рядов
Важнейшей задачей при исследовании временных рядов является выявление и статистическая оценка основной тенденции развития изучаемого процесса и отклонений от нее.
Отметим основные этапы анализа временных рядов:
· графическое представление и описание временного ряда;
· выделение и удаление закономерных (неслучайных) составляющих временного ряда (тренда, сезонных и циклических составляющих);
· сглаживание и фильтрация (удаление низко- и высокочастотных составляющих временного ряда);
· исследование случайной составляющей временного ряда, построение и проверка адекватности математической модели для ее описания;
· прогнозирование развития изучаемого процесса на основе имеющегося временного ряда;
· исследование взаимосвязи между различными временными рядами [1, с 135].
Среди наиболее распространенных методов анализа временных рядов выделим корреляционный и спектральный анализ, модели авторегрессии, скользящей средней и авторегрессионная модель скользящей средней.
Распространенным способом моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называется аналитическим выравниванием временного ряда.
Поскольку зависимость от времени может принимать различные формы, для ее формализации можно использовать различные виды функции. Для построения трендов чаще всего применяются следующие функции:
тренд в форме степенной функции:
парабола второго и более порядков:
Аналитическое выравнивание есть не что иное, как удобный способ описания эмпирических данных. Общие соображения при выборе типа линии, по которой производится аналитическое выравнивание, могут быть сведены к следующим:
1) Если абсолютные приросты уровней ряда по своей величине колеблются около постоянной величины, то математической функцией, уравнение которой можно принять за основу аналитического выравнивания, следует считать прямую линию:
где yt считается как у, выровненный по t.
2) Если приросты приростов уровней, то есть ускорения, колеблются около постоянной величины, то за основу аналитического выравнивания, следует принять параболу второго порядка:
Показатели а0, а1 и а2 представляют собой в каждом отдельном случае выравнивания постоянные величины, называемые параметрами:
3) Если уровни изменяются с приблизительно постоянным относительным приростом, то выравнивание производится по показательной (экспонентной функции):
В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путём сравнения коэффициентов автокорреляции первого порядка, рассчитанным по исходным и преобразованным уровням ряда.
Если временной ряд имеет линейную тенденцию, то его соседние уровни yt и y t -1 тесно коррелируют.
В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким.
Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда.
Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.
Одна из рабочих формул для расчёта коэффициента автокорреляции имеет вид:
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости её значений от величины лага (порядка коэффициента корреляции) называется коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а, следовательно, и лаг, при котором связь между текущим и предыдущими уровнями ряда наиболее тесная, то есть при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию.
Если наиболее высоким оказался коэффициент автокорреляции порядка k, ряд содержит циклические колебания с периодичностью в k моментов времени.
Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.
Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты и циклической, сезонной компоненты [5, с 110].
Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок для анализа взаимосвязи исходного ряда и других временных рядов.
временной ряд коррелограмма адаптивный
Изменения значений уt во времени в реальной жизни обычно происходят под воздействием каких-либо причин, факторов.
Однако в силу их многочисленности, сложности измерения, не разработанности теоретических предположений относительно взаимосвязей с переменной у и т. п. обосновать и построить “подходящую” для описания процесса уt, t=1,2. многофакторную эконометрическую модель классического типа не всегда представляется возможным.
В результате в отношении ряда уt часто выдвигается предположение, что совокупное влияние этих факторов формирует как бы внутренние закономерности в развитии процесса уt, что дает возможность применить для его описания эконометрическую модель из специфического класса моделей временных рядов [4, с 253].
Общим для всех моделей временных рядов является предположение о том, что текущее значение процесса yt в значительной степени предопределено его предысторией, т. е. величина показателя yt генерируется значениями yt-1, yt-2. согласно характерным для этого временного ряда закономерностям. Математически это допущение может быть выражено следующим общим уравнением:
где, как и ранее, t представляет собой ошибку модели в момент t.
Для широкого круга процессов функция f имеет линейный вид.
Линейные модели временных рядов применяются, как правило, для описания стационарных процессов. При этом обычно имеются в виду стационарные процессы второго порядка.
Напомним, что стационарный процесс п-го порядка характеризуется постоянными значениями всех своих моментов порядка п и ниже на всех временных отрезках, входящих в интервал t=1,2. Т. У строго стационарных процессов постоянными являются моменты всех порядков.
Таким образом, для любых двух интервалов времени (Т1, Т2) и (Т3, Т4) для стационарного процесса второго порядка уt должны выполняться условия, характеризующие равенство на рассматриваемых интервалах математических ожиданий, дисперсий и однопорядковых коэффициентов автокорреляций исследуемого процесса [4, с 255].
Стационарные временные ряды применяются, в частности, при описании случайных составляющих анализируемых рядов. При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня зависят от предыдущих.
Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровня ряда.
Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.
Формула для расчета коэффициента автокорреляции имеет вид:
Эту величину называют коэффициентом автокорреляции уровней первого порядка, так как он измеряет зависимость между соседними уровнями ряда yt и yt-1.
Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков.
Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом.
Максимальный лаг должен быть не более n/4. Коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия и отсутствия трендовой компоненты и циклической компоненты.
Рассмотрим модель, в которых регрессорами выступают лаговые переменные, т.е. переменные, влияние которых в эконометрической модели характеризуется некоторым запаздыванием. Переменные в данной модели являются величины случайные.
Все множество стационарных процессов второго порядка в общем случае в зависимости от особенностей их автокорреляционных функций разбивается на несколько однородных групп, для каждой из которых можно подобрать и построить адекватную модель.
Эта модель описывает изучаемый процесс в момент t в зависимости от его значений в предыдущие моменты t-1, t-2, …, t-р.
Модель скользящей средней в ней моделируемая величина задается линейной функцией от возмущений (ошибок) в предыдущие моменты времени.
Модель скользящей средней q-го порядка (или модель? МА (q)), имеет вид:
yt =?+ y1?(t-1) + y2?(t-2) +…+ yq?(t-q) (2.4)
В эконометрике используются также комбинированные модели временных рядов AR и МА.
Использование авторегрессионных моделей, на базе рассмотренных моделей, для прогнозирования экономических показателей может оказаться весьма эффективным только в краткосрочной перспективе.
Статистические методы все шире проникают в экономическую практику. С развитием компьютеров, распространением пакетов прикладных программ эти методы вышли за стены учебных и научно-исследовательских институтов. Они стали важным инструментом в деятельности аналитических, плановых, маркетинговых отделов различных фирм и предприятий.
При прогнозировании часто исходят из того, что уровни временных рядов экономических показателей, состоят из четырех компонент: тренда, сезонной, циклической и случайной составляющих. В зависимости от способа сочетания этих компонент модели временных рядов делятся на аддитивные, мультипликативные модели.
Обобщенными показателями динамики развития экономических процессов являются средний прирост, средний темп роста и прироста. При выполнении ряда предпосылок эти показатели могут быть использованы в приближенных, простейших способах прогнозирования, предшествующих более глубокому количественному и качественному анализу.
Распространенным приемом при выявлении тенденции развития является выравнивание временных рядов, в частности, с помощью скользящих средних. Скользящие средние позволяют сгладить как случайные, так и периодические колебания, выявить имеющуюся тенденцию в развитии процесса.
Для того, чтобы обоснованно судить о качестве полученной модели необходимо проверить адекватность этой модели реальному процессу и проанализировать характеристики ее точности.
Проверка адекватности строится на анализе случайной компоненты и базируется на использовании ряда статистических критериев. Показатели точности описывают величины случайных ошибок, полученных при использовании модели.
Все характеристики точности могут быть вычислены после того, как период упреждения уже окончился, или при рассмотрении показателя на ретроспективном участке.
Одно из перспективных направлений развития краткосрочного прогнозирования связано с адаптивными методами.
Эти методы позволяют строить самокорректирующиеся модели, способные оперативно реагировать на изменение условий.
Адаптивные методы учитывают различную информационную ценность уровней ряда, «старение» информации. Все это делает эффективным их применение для прогнозирования неустойчивых рядов с изменяющейся тенденцией.
В заключение отметим, что не может быть чисто формальных подходов к выбору методов и моделей прогнозирования. Успешное применение статистических методов прогнозирования на практике возможно лишь при сочетании знаний в области самих методов с глубоким знанием объекта исследования, с содержательным экономическим анализом.
1. Эконометрика. Кремер Н.Ш., Путко Б.А., М.:ЮНИТИ-ДАНА, 2002, с.311
2. Эконометрика. Учебник под ред. Елисеевой И.И., М.:Финансы и статистика, 2003, с. 344
3. Эконометрика. Орлов А.И., М.:Экзамен, 2002, с. 576
4. Эконометрика. Тихомиров Н.П., Дорохина Е.Ю., М.:Издательство Российская экономическая академия, 2002, с. 640
5. Эконометрика. Учебно-методическое пособие, Шалобанов А.К., Роганов Д.А., Казань:КазГУ, 2008, с. 198
6. Эконометрика в схемах и таблицах. Под ред. Орехова С.А., М.:Эксмо, 2008, с. 224
7. Эконометрика. Конспект лекций, Яковлева А.В., М.:Эксмо, 2008, с. 224
8. Эконометрика. Начальный курс. Магнус Я.Р., Катышев П.К., Пересецкий А.А., 6-е изд., перераб. и доп., М.:Дело, 2004, с. 576
Размещено на Allbest.ru
Подобные документы
Основные элементы эконометрического анализа временных рядов. Задачи анализа и их первоначальная обработка. Решение задач кратко- и среднесрочного прогноза значений временного ряда. Методы нахождения параметров уравнения тренда. Метод наименьших квадратов.
контрольная работа [37,6 K], добавлен 03.06.2009
Временные ряды и их характеристики. Факторы, влияющие на значения временного ряда. Тренд и сезонные составляющие. Декомпозиция временных рядов. Метод экспоненциального сглаживания. Построение регрессионной модели. Числовые характеристики переменных.
контрольная работа [1,6 M], добавлен 18.06.2012
Классические подходы к анализу финансовых рынков, алгоритмы машинного обучения. Модель ансамблей классификационных деревьев для прогнозирования динамики финансовых временных рядов. Выбор алгоритма для анализа данных. Практическая реализация модели.
дипломная работа [1,5 M], добавлен 21.09.2016
Статистические методы анализа одномерных временных рядов, решение задач по анализу и прогнозированию, построение графика исследуемого показателя. Критерии выявления компонент рядов, проверка гипотезы о случайности ряда и значения стандартных ошибок.
контрольная работа [325,2 K], добавлен 13.08.2010
Теоретические выкладки в области теории хаоса. Методы, которые используются в математике, для прогнозирования стохастических рядов. Анализ финансовых рядов и рядов Twitter, связь между сентиметными графиками и поведением временного финансового ряда.
курсовая работа [388,9 K], добавлен 01.07.2017
Структурные компоненты детерминированной составляющей. Основная цель статистического анализа временных рядов. Экстраполяционное прогнозирование экономических процессов. Выявление аномальных наблюдений, а также построение моделей временных рядов.
курсовая работа [126,0 K], добавлен 11.03.2014
Анализ временных рядов с помощью статистического пакета «Minitab». Механизм изменения уровней ряда. Trend Analysis – анализ линии тренда с аппроксимирующими кривыми (линейная, квадратическая, экспоненциальная, логистическая). Декомпозиция временного ряда.
методичка [1,2 M], добавлен 21.01.2011



