Что относится к логическим операциям
Логические операции и выражения
Логика
Логические операции и выражения
Таблица истинности
Логический элемент
Логика это не просто древнегреческое слово, а целая наука, изучение которой позволяет нам правильно и здраво рассуждать, и, соответственно, делать правильные выводы из наших рассуждений, чего, однако, очень не хватает в нашем современном мире (поэтому и говорят «нелогичный человек», «нелогичный поступок»).
Рассуждая о чем-либо, мы, на основе логических заключений, делаем соответствующие выводы. К примеру, думая о своем товарище, на основе каких-то фактах, характеризующих его, мы можем сделать вывод – друг он нам, или нет (или: «и не друг, и не враг, – а так»).
Основные логические операции
Существует три основных логических операции при помощи которых можно записать любое логическое выражение (не пугайтесь):
1. Инверсия
2. Конъюнкция
3. Дизъюнкция
Таблица истинности
Все логические выражения, получающиеся из логических операций, можно свести в таблицы, которые называются таблицы истинности
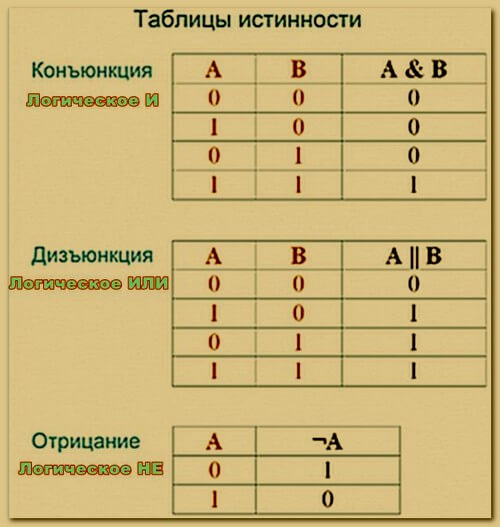
Таблицы истинности
Логические элементы
Логический элемент выполняющий операцию «Логическое И»
Логический элемент выполняющий операцию «Логическое ИЛИ»
Логический элемент выполняющий операцию «Логическое НЕ»
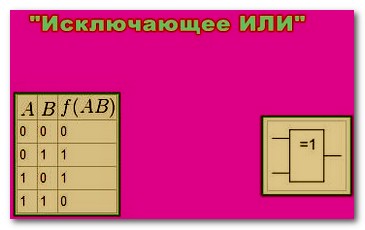
Логический элемент выполняющий операцию «Исключающее ИЛИ»
Логический элемент выполняющий операцию «Логическое ИЛИ-НЕ»
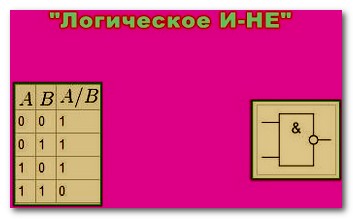
Логический элемент выполняющий операцию «Логическое И-НЕ»
Кроме таких комбинаций логических операций существует еще ряд других.
Кстати, есть еще одна разновидность логики – женская логика. Весьма интересная штука. Но так как она к сегодняшней теме не относится, то придется, к сожалению, этот вопрос опустить.


Логические операции. ➞ Что такое конъюнкция, дизъюнкция, импликация
Тот, кто хочет подробно разбираться в цифровых технологиях должен понимать основы такой темы, как алгебра логики. В этой статье будут разобраны основные определения, а также показаны самые важные логические операции, такие как конъюнкция, дизъюнкция, импликация и т.д.
Основные положения
Для начала следует разобраться, для чего нужна алгебра логики – главным образом, этот раздел математики и информатики, нужен для работы с логическими выражениями и высказываниями.
Логическим высказыванием называется утверждение (или запись), которое мы можем однозначно классифицировать, как истинное или ложное (1 или 0 в информатике).
Примером таким высказываний будут являться:
Логические высказывания делятся на два типа — простые и сложные.
В алгебре логики, как простые, так и сложные высказываниями описываются булевыми выражениями.
Булево выражение – это символическое (знаковое) описание высказывания.
Операции
Ниже рассмотрим основные операции, которые применяются в булевой алгебре. Их хватит, чтобы упростить львиную долю всех выражений, которые Вам встретятся.
Конъюнкция
Конъюнкция (булево умножение) — функция, по своему смыслу приближенная к союзу «И». При выполнении конъюнкции результат истинен (равен 1) тогда и только тогда, когда истинны ВСЕ переменные. Если хотя бы одно из высказываний ложно, то ложно и всё выражение (равно 0).
Функция может работать как с двумя операндами (высказываниями), так и с тремя, четырьмя и т.д. В математике обозначается с помощью знаков \( \wedge \) и &. Обозначение в языках программирования AND, &&. Таблица истинности для двух операндов:
Дизъюнкция
Дизъюнкцией называется функция булева сложения. По смыслу дизъюнкция приближена к союзу «ИЛИ». В результате выполнения данной функции результирующие выражение является истинным, когда хотя бы одно из высказываний в этом выражении тоже истинно.
Булево сложение, также как и умножение, может работать с произвольным количеством операндов. В математике обозначается как V, а в программировании с помощью OR или I.
Инверсия
Логическое отрицание – функция, работающая с одним высказыванием, и заменяющая истину на ложь, а ложь на истину. В математике обозначается с помощью черты над значением, а в программирование и информатике с помощью слова NOT.
Импликация
Также называется булевым следованием. В русском языке данной функции соответствует оборот «Если …, то …». Например, если на улице гремит гром, то стоит пасмурная погода.
Эквивалентность
Булева тождественность или равенство. На простом языке будет обозначено как «… эквивалентно (равно) …». Результат будет истинным тогда, когда все значения в выражении будут иметь одинаковую истинность.
Обозначается с помощью трех черточек или ⟺.
Порядок выполнения операций
Логические операции выполняются в следующем порядке:
Если в формуле указаны скобки, то порядок выполнения действий в скобках точно такой же, как написано выше.
Пример
Дано два отрезка B = [2,10], C = [6,14]. Из предложенных вариантов ответа выберите такой отрезок A, что формула \( ((z \in A) \Longrightarrow (z \in B)) \vee (z \in C) \) истинна при любом значении z. Варианты ответа:
Решение: Подставим в уравнение \( ((z \in A) \Longrightarrow (z \in B)) \vee (z \in C) \) =1 значения B и C и составим таблицу истинности:
Получившаяся формула \( ((z \in A) \Longrightarrow (z \in [2,10])) \vee (z \in [6,14])=1 \). По условию \( z \in A \)=1.
Таблица истинности для всех отрезков:
Ответ: A = [3,11].
Видео
Заключение
Вот Вы и познакомились с основными логическими операциями и понятиями и знаете, что такое булево сложение и умножение. Если вас заинтересовала данная тема, то можете изучить булевы законы. Эти законы не проходятся в рамках школьной программы и служат для упрощения сложных выражений.
Что относится к логическим операциям

2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.
Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.
Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.
С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.
Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.
Существуют разные варианты обозначения истинности и ложности логических переменных:
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.
Введем перечисленные логические операции.
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Что относится к логическим операциям
Наука, изучающая формы, методы и законы правильного мышления, называется логикой. Она интересуется не содержанием мышления, а его формой, поэтому ее часто называют еще формальной логикой.
Форма мышления — это способ выражения мыслей или форма, по которой они строятся.
Форма, обозначающая какой–либо объект или отличающий его признак, называется понятием. Примеры понятий: «компьютер», «планета», «длина», «профессия».
Форма, утверждающая или отрицающая что–либо о свойствах понятий и отношений между ними, называется утверждением (высказыванием, суждением). Примеры логических утверждений: «Декодирование — процесс восстановления информации из закодированного представления»; «В двоичной системе используются две цифры: 0 и 1»; «Париж — столица Франции». Утверждения могут быть истинными или ложными. Так, высказывание «Шанхай — столица Франции» является ложным утверждением.
Форма, в которой из двух или нескольких высказываний получают новое утверждение, называется умозаключением. Пример умозаключения: «Периферийные устройства компьютера — это устройства для ввода или вывода информации. Сканер — устройство для переноса текста и изображений с бумаги в компьютер. Следовательно, сканер — периферийное устройство».
Правила, которые должны соблюдаться, чтобы на основании истинных суждений получить истинные выводы, — это законы мышления. Логика изучает эти законы и способы получения новых утверждений на основании уже имеющихся.
Математическая логика использует для установления истинности или ложности высказываний математические методы. Она пользуется специальным символьным языком, подобным языку математики, поэтому ее часто называют символьной логикой.
Алгебра логики — раздел математической логики, в котором методы алгебры используются в логических преобразованиях. Она изучает логические высказывания и методы установления их истинности или ложности с помощью алгебраических методов.
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно. Вопросительные и повелительные предложения не являются логическими высказываниями. Но и не каждое повествовательное предложение является логическим высказыванием. Например, суждение «Лето было очень дождливым» не является однозначным, для утверждения «Существует несколько Вселенных» нельзя однозначно определить истинность; поэтому такие предложения не являются логическими высказываниями (утверждениями).
Таким образом, отличительной особенностью логических высказываний является возможность принимать одно из двух значений — истина и ложь. Истинность или ложность высказывания определяется вне алгебры логики — с помощью наблюдений, научных исследований, практических опытов и т. п.
В алгебре логики различают простые высказывания и сложные (составные), составленные из нескольких простых. Если в высказывании нельзя выделить некую часть, которая не совпадает по смыслу с исходным высказыванием и сама является высказыванием, то оно называется простым высказыванием. Простые высказывания обычно обозначаются латинскими буквами A, B, C и т. д.
Сложные высказывания представляют собой объединение простых высказываний с помощью логических связок. В качестве логических связок используются слова «не», «и», «или», «тогда и только тогда», «если … то». Истинность или ложность получаемых таким образом сложных высказываний определяется значением простых высказываний. Например, из простых высказываний «Офис фирмы находится в Мадриде» и «Офис фирмы находится в Берлине» можно составить сложные: «Офис фирмы находится в Мадриде или Берлине», «Офис фирмы находится в Мадриде и Берлине», «Если офис фирмы находится в Мадриде, то он находится в Берлине». Истинность первого из них означает, что офис фирмы находится в одном из названных городов или же имеются офисы в обоих городах. Ложность его означает, что ни в одном из этих городов офиса нет. Второе составное утверждение истинно тогда, когда в обоих городах имеется офис фирмы. Если же офис существует только в Берлине или только в Мадриде, — второе составное высказывание ложно.
В классической, двузначной алгебре логики логических значений всего два: истина (True) и ложь (False). Им соответствует цифровое представление — 1 и 0. Иногда эти значения записывают как «да» и «нет». Факт истинности или ложности некоторого высказывания А записывают соответственно как А = 1 или А = 0.
Логические операции
В алгебре логики логические связки рассматриваются как логические операции. Они имеют свои названия и обозначения. Результаты применения каждой операции к логическим высказываниям (истинным или ложным) можно представить в виде таблицы. В ней указывают все возможные сочетания значений исходных логических высказываний и истинность или ложность результата. Такие таблицы называют таблицами истинности операции. Обычно в них используют обозначения логических значений 0 и 1 или ложь и истина.
Основные логические операции — отрицание, конъюнкция, дизъюнкция, исключающая дизъюнкция, следование, эквивалентность.
Логическое отрицание (инверсия) — логическая операция, в результате которой из данного высказывания получается новое высказывание — отрицание исходного. Обозначается символически чертой сверху (Ā) или условными обозначениями ¬А, not А, не А (читается «отрицание А», «не А», «А ложно», «неверно, что А»).
Высказывание ¬А ложно, когда А истинно, и истинно, когда А ложно.
Таблица истинности операции отрицания
Если обозначить через А высказывание «Арбуз является ягодой», то ¬А соответствует высказыванию «Арбуз не является ягодой» («Неверно, что арбуз — ягода»).
Отрицание является унарной операцией. Унарная (одноместная) операция — это операция, которая применяется к одному операнду.
Остальные логические операции являются двуместными (бинарными). Бинарная (двуместная) операция — это операция, которая выполняется над двумя операндами.
Логическое умножение (конъюнкция) — операция, соединяющая два или более высказываний при помощи связки «и». Эта связка символически обозначается с помощью знака ∧ и читается «А и В». Для обозначения конъюнкции также применяются знаки: А • В, А & В, А и В, А and В, а иногда между высказываниями не ставится никакого знака: АВ.
Высказывание А ∧ В истинно только тогда, когда оба высказывания А и В истинны. Высказывание А ∧ В ложно только тогда, когда ложно хотя бы одно из высказываний А или В.
Таблица истинности операции конъюнкции
Например, высказывания «Лондон расположен севернее Лиссабона» и «Лондон расположен восточнее Лиссабона» истинны. Тогда истинным будет и составное логическое высказывание «Лондон расположен севернее и восточнее Лиссабона». Высказывания «Лондон расположен не севернее и восточнее Лиссабона», «Лондон расположен севернее и не восточнее Лиссабона», «Лондон расположен не севернее и не восточнее Лиссабона» — ложны.
Логическое сложение (дизъюнкция) — операция, соединяющая два или более высказываний при помощи связки « или». Эта связка символически обозначается с помощью знака v и читается «А или В». Для обозначения дизъюнкции также применяются знаки: А + В, А или В, А or В, А | B.
Высказывание А v В истинно только тогда, когда хотя бы одно из высказываний А или В истинно. Высказывание А v В ложно только тогда, когда оба высказывания А и В ложны.
Таблица истинности операции дизъюнкции
Например, высказывания «Виктор старше Ольги» и «Виктор — однофамилец Ольги» истинны. Тогда истинными будут и составные логические высказывания «Виктор старше Ольги или Виктор — однофамилец Ольги», «Виктор младше Ольги или Виктор — однофамилец Ольги», «Виктор старше Ольги или Виктор — не однофамилец Ольги». Высказывание «Виктор младше Ольги или Виктор — не однофамилец Ольги» — ложно, поскольку ложны оба составляющие его простые высказывания.
Исключающее сложение (исключающая дизъюнкция, строгая дизъюнкция, сложение по модулю два, дизъюнкция строго–разделительная) — логическая операция, соединяющая два высказывания при помощи связки «или», употребленной в исключающем смысле (называется также исключающее «или»). Операция символически обозначается с помощью знака ⊕ и читается «либо А, либо В».
Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.
Таблица истинности операции строгой дизъюнкции
Например, результат исключающей дизъюнкции двух высказываний «Виктор не старше Ольги» и «Виктор младше Ольги» всегда будет истиной, кто бы из них не был старше.
Логическое следование (импликация) — логическая операция, соединяющая два высказывания при помощи связки «если… то» в сложное высказывание. Операция символически обозначается с помощью знака → и читается «Если А, то В», «А влечет В», «из А следует В», «А имплицирует В». Для обозначения импликации применяются также знаки ⊃ или ⇒. Первое логическое высказывание является условием (посылкой), а второе — следствием (заключением).
Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина. Таким образом, импликация А → В ложна только тогда, когда А истинно, а В ложно (из истинного высказывания следует ложное). Во всех остальных случаях импликация истинна.
Таблица истинности операции импликации
Для высказываний «Луна — спутник Земли» и «Сумма углов треугольника не равна 180°» (первое истинно, второе ложно) составное высказывание «Если Луна — спутник Земли, то сумма углов треугольника не равна 180°» будет ложным. Однако истинными будут высказывания «Если Луна — спутник Земли, то сумма углов треугольника равна 180°», «Если Луна — не спутник Земли, то сумма углов треугольника не равна 180°» и «Если Луна — не спутник Земли, то сумма углов треугольника равна 180°». Этот пример наглядно демонстрирует, что в алгебре логики смысл высказываний не учитывается, а рассматриваются только их истинность или ложность.
Логическое равенство (эквивалентность, следование, двойная импликация, равнозначность) — логическая операция, позволяющая из двух высказываний А и В получить новое высказывание А ≡ В (читается «А эквивалентно B»). Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Для обозначения эквивалентности применяются знаки
Если оба высказывания имеют различные логические значения, результатом операции эквивалентности всегда будет ложь. Если же оба простые высказывания ложны или оба истинны, то составное логическое высказывание всегда будет истинно.
Таблица истинности операции эквивалентности
Для высказываний «Линейное уравнение всегда имеет решение» и «Кит — млекопитающее» их эквивалентность всегда будет истиной, так как оба простые утверждения истинны.
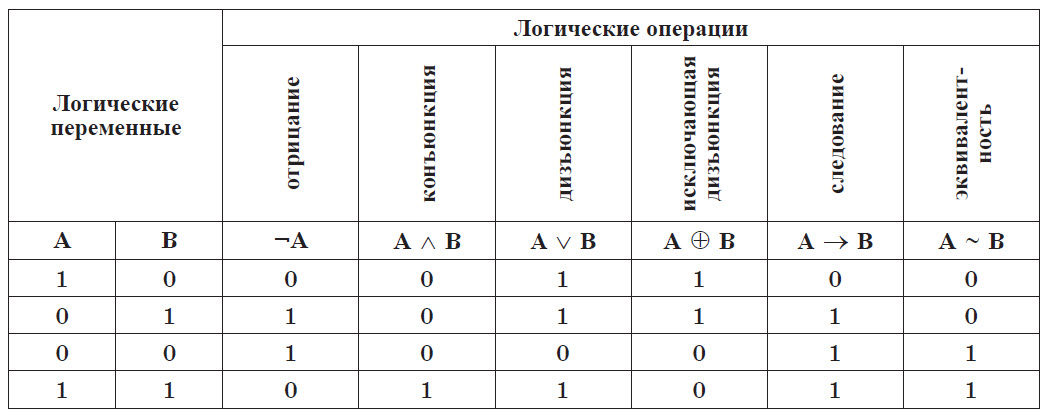
Таким образом, сводная таблица истинности для всех основных логических операций имеет вид:
Логические выражения
Логические высказывания могут быть записаны в виде формул (логических выражений). Логические выражения включают логические переменные, знаки логических операций, логические константы (истина и ложь) и скобки. Логические выражения принимают значения истина или ложь.
Правила построения логических выражений:
В — тоже логические выражения.
Например, A ⊕ истина v В v ложь — логическое выражение; А v ⊕ В v ложь не является логическим выражением.
Логическое выражение, принимающее значение истина при любых значениях входящих в него переменных, называется тождественно–истинным выражением (тавтологией). Например, А v В v ¬А; (А ∧ ¬А) → В.
Логическое выражение, принимающее значение ложь при любых значениях входящих в него переменных, называется тождественно–ложным выражением (противоречием). Например, А ∧ ¬А; В
Логическое выражение, принимающее как значение ложь, так и значение истина при разных значениях входящих в него переменных, называется выполнимым выражением.
ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ
Для сложных логических выражений, содержащих несколько логических операций, определен порядок выполнения действий (приоритет): сначала операции отрицания, затем операции логического умножения, потом операции логического сложения и исключающего сложения, последними выполняются операции импликации и эквивалентности. Операции выполняются слева направо. Порядок выполнения может быть изменен с помощью скобок.
Приоритет выполнения логических операций в логических выражениях
Пример 1
Определить порядок выполнения логических операций в выражении.
Вычислить его значение, если А = 1, В = 0, С = 1.
¬А ∧ С v (A ⊕ В) ∧ В
Решение. Первыми вычисляются значения в скобках. Затем выполняются операции по приоритетам: самый высокий приоритет имеет операция отрицания, после нее, как в математике, следуют операции умножения, а затем сложения. Таким образом, порядок будет следующий:
Тогда значение выражения ¬1 ∧ 1 v (1 ⊕ 0) ∧ 0 после вычисления отрицания и выражения в скобках: 0 ∧ 1 v 1 ∧ 0, после операций умножения: 0 v 0. Итог: 0.
Ответ: логическое выражение ложно.
Пример 2
Для каких из приведенных слов истинно следующее высказывание?
(Вторая буква гласная) ИЛИ (Первая буква гласная) И НЕ (Длина имени не больше 5 букв)
1) Олег 2) Марианна 3) Светлана 4) Ольга.
СВЯЗЬ МЕЖДУ ЛОГИЧЕСКИМИ ОПЕРАЦИЯМИ
Между логическими операциями существует взаимосвязь. Операции исключающего «или», следования и эквивалентности можно выразить через операции отрицания, логического сложения и умножения, что отражено в следующей таблице.
Связь между логическими операциями
Поэтому операции отрицания, логического сложения и логического умножения называют основными логическими операциями: их достаточно, чтобы построить любое логическое выражение.
Если логическое выражение содержит только операции отрицания, логического сложения и логического умножения, говорят, что выражение находится в нормальной форме.
РАВНОСИЛЬНЫЕ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ
Логические выражения, значения которых совпадают для всех наборов входящих в них переменных, называются равносильными, или эквивалентными.
Чтобы убедиться, что два выражения равносильны, можно построить для них таблицы истинности. Если в таблицах совпадут все значения, значит, выражения равносильны.
Пример 3
Проверить равносильность выражений А
Решение. Для проверки следует создать таблицу истинности, содержащую столько строк, сколько возможно наборов значений переменных, входящих в выражение. Для двух переменных (А и E) количество наборов равно четырем. К двум столбцам для значений переменных (А и E) нужно присовокупить количество столбцов, равное количеству операций в выражении. Таким образом, необходимо создать таблицу, содержащую 4 строки и 7 столбцов.
Заполним первые 2 столбца (А и E) всеми сочетаниями значений переменных. Запишем в качестве заголовков столбцов все операции выражения в порядке их выполнения (в соответствии с приоритетами и скобками). Рассчитаем значения этих операций: сначала выражения в скобках, затем результат их сложения.
Последний столбец содержит результирующее значение выражения. Он совпадает с таблицей истинности для операции эквивалентности. Следовательно, выражения равносильны.
Основные законы алгебры логики
Для сложных логических выражений с большим числом переменных определение их истинности путем построения таблиц истинности становится громоздким. В таких случаях применяют способы упрощения выражений. Под упрощением понимают равносильное преобразование выражения к его нормальной форме.
Нормальная форма выражения содержит только операции отрицания, конъюнкции и дизъюнкции и не содержит отрицания выражений и двойных отрицаний.
Для упрощения используют равносильные преобразования, которые иначе называют основными законами алгебры логики.
Тождественные преобразования логических выражений
Для всех тождественных преобразований выполняется закон двойственности: если в формуле преобразования заменить конъюнкцию на дизъюнкцию, дизъюнкцию — на конъюнкцию, значения 1 — на 0, 0 — на 1, то закон, сформулированный для конъюнкции, примет форму аналогичного закона для дизъюнкции, и наоборот.
Прежде всего при равносильных преобразованиях избавляются от отрицания выражений, потом — от логических операций исключающей дизъюнкции, следования и эквивалентности. Затем используют законы алгебры логики для уменьшения количества переменных в выражении.
Пример 4
Выбрать выражение, которое равносильно выражению (A ∧ B) v (Ā ∧ B).
1) A 2) A ∧ B 3) Ā ∧ B 4) B
Решение. В соответствии с законом склеивания (A ∧ B) v (Ā ∧ B) = B, следовательно, исходное выражение равносильно выражению В.
Ответ: 4) В.
ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ
Выражения, которые принимают логические значения (истина или ложь) в результате выполнения операций сравнения (больше >, меньше 3
Решение. В соответствии с приоритетами операций сначала следует выполнить операции сравнения, затем отрицания, а потом — конъюнкцию. Отрицанием высказывания М ≥ 10 является высказывание М 3. Для того чтобы это выражение (конъюнкция) было истинным, должны выполняться (т. е. быть истинными) оба неравенства. Следовательно, значение М должно быть больше 3, но меньше 10. Среди предложенных значений этому условию удовлетворяет только одно — число 4.
Ответ: 4) 4.
Задачи, подобные предыдущему примеру, можно решать и с помощью таблиц истинности.
Пример 6.
Для какого из приведенных ниже значений числа М истинно следующее выражение?
¬М ≥ 10 ∧ M > 3
Решение. Составим таблицу истинности: все операции выражения укажем в столбцах таблицы, все предложенные значения М укажем в ее строках. Рассчитаем значения таблицы:
Последний столбец содержит результат всего выражения. Истинным оно будет только для значения числа М, равного 4.
Ответ: 4) 4.
Пример 7.
В табличной форме представлены ежемесячные данные о продаже групп товаров за полгода. Сколько групп товаров демонстрировали рост продаж в весенние месяцы или вышли на уровень свыше 80 % в июне?
Решение. Переформулируем условие задачи: необходимо найти группы товаров, для которых (Март 80).
Введем обозначения:
А = (Март 80)
Тогда выражение можно записать как А ∧ В v С.
Логическое выражение состоит из одной конъюнкции и одной дизъюнкции. Значение выражения конъюнкции истинно только тогда, когда истинны оба составляющие его простых выражения ((Март
Конспект урока по информатике «Логические значения, операции, выражения».