Что открыл гаусс в математике
Гаусс, Карл Фридрих
Содержание
Биография
1777—1798 годы
Дед Гаусса был бедным крестьянином, отец — садовником, каменщиком, смотрителем каналов в герцогстве Брауншвейг. Уже в двухлетнем возрасте мальчик показал себя вундеркиндом. В три года он умел читать и писать, даже исправлял счётные ошибки отца. Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 
До самой старости он привык большую часть вычислений производить в уме.
С учителем ему повезло: М. Бартельс (впоследствии учитель Лобачевского) оценил исключительный талант юного Гаусса и сумел выхлопотать ему стипендию от герцога Брауншвейгского. Это помогло Гауссу закончить колледж Collegium Carolinum в Брауншвейге (1792—1795).
Свободно владея множеством языков, Гаусс некоторое время колебался в выборе между филологией и математикой, но предпочёл последнюю. Он очень любил латинский язык и значительную часть своих трудов написал на латыни; любил английскую, французскую и русскую литературу. В возрасте 62 лет Гаусс начал изучать русский язык, чтобы ознакомиться с трудами Лобачевского, и вполне преуспел в этом деле.
В колледже Гаусс изучил труды Ньютона, Эйлера, Лагранжа. Уже там он сделал несколько открытий в теории чисел, в том числе доказал закон взаимности квадратичных вычетов. Лежандр, правда, открыл этот важнейший закон раньше, но строго доказать не сумел; Эйлеру это также не удалось. Кроме этого, Гаусс создал «метод наименьших квадратов» (тоже независимо открытый Лежандром) и начал исследования в области «нормального распределения ошибок».
С 1795 по 1798 год Гаусс учился в Гёттингенском университете. Это наиболее плодотворный период в жизни Гаусса.
1796 год: Гаусс доказал возможность построения с помощью циркуля и линейки правильного семнадцатиугольника. Более того, он разрешил проблему построения правильных многоугольников до конца и нашёл критерий возможности построения правильного n-угольника с помощью циркуля и линейки: если n — простое число, то оно должно быть вида 
С 1796 года Гаусс ведёт краткий дневник своих открытий. Многое он, подобно Ньютону, не публиковал, хотя это были результаты исключительной важности (эллиптические функции, неевклидова геометрия и др.). Своим друзьям он пояснял, что публикует только те результаты, которыми доволен и считает завершёнными. Многие отложенные или заброшенные им идеи позже воскресли в трудах Абеля, Якоби, Коши, Лобачевского и др. Кватернионы он тоже открыл за 30 лет до Гамильтона (назвав их «мутациями»).
Все многочисленные опубликованные труды Гаусса содержат значительные результаты, сырых и проходных работ не было ни одной.
1798 год: закончен шедевр «Арифметические исследования» (лат. Disquisitiones Arithmeticae ), напечатан только в 1801 году.
В этом труде подробно излагается теория сравнений в современных (введенных им) обозначениях, решаются сравнения произвольного порядка, глубоко исследуются квадратичные формы, комплексные корни из единицы используются для построения правильных n-угольников, изложены свойства квадратичных вычетов, приведено доказательство квадратичного закона взаимности и т. д. Гаусс любил говорить, что математика — царица наук, а теория чисел — царица математики.
1798—1816 годы
В 1798 году Гаусс вернулся в Брауншвейг и жил там до 1807 года.
Герцог продолжал опекать молодого гения. Он оплатил печать его докторской диссертации (1799) и пожаловал неплохую стипендию. В своей докторской Гаусс впервые доказал основную теорему алгебры. До Гаусса было много попыток это сделать, наиболее близко к цели подошёл Д’Аламбер. Гаусс неоднократно возвращался к этой теореме и дал 4 различных её доказательства.
С 1799 года Гаусс — приват-доцент Брауншвейгского университета.
После 1801 года Гаусс, не порывая с теорией чисел, расширил круг своих интересов, включив в него и естественные науки. Катализатором послужило открытие малой планеты Церера (1801), вскоре после наблюдений потерянной. 24-летний Гаусс проделал (за несколько часов) сложнейшие вычисления по новому, открытому им же методу, и указал место, где искать беглянку; там она, к общему восторгу, и была вскоре обнаружена.
Слава Гаусса становится общеевропейской. Многие научные общества Европы избирают Гаусса своим членом, герцог увеличивает пособие, а интерес Гаусса к астрономии ещё более возрастает.
1805 год: Гаусс женился на Иоганне Остгоф. У них было трое детей.
1806 год: от раны, полученной на войне с Наполеоном, умирает его великодушный покровитель-герцог. Несколько стран наперебой приглашают Гаусса на службу (в том числе в Петербург). По рекомендации Александра фон Гумбольдта Гаусса назначают профессором в Гёттингене и директором Гёттингенской обсерватории. Эту должность он занимал до самой смерти.
1807 год: наполеоновские войска занимают Гёттинген. Все граждане облагаются контрибуцией, в том числе огромную сумму — 2000 франков — требуется заплатить Гауссу. Ольберс и Лаплас тут же приходят ему на помощь, но Гаусс отклоняет их деньги; тогда неизвестный из Франкфурта присылает ему 1000 гульденов, и этот дар приходится принять. Только много позднее узнали, что неизвестным был курфюрст Майнцский, друг Гёте.
1809 год: новый шедевр, «Теория движения небесных тел». Изложена каноническая теория учёта возмущений орбит.
Как раз в четвёртую годовщину свадьбы умирает Иоганна, вскоре после рождения третьего ребёнка. В Германии разруха и анархия. Это самые тяжёлые годы для Гаусса.
1810 год: новая женитьба, на Минне Вальдек, подруге Иоганны. Число детей Гаусса вскоре увеличивается до шести.
1811 год: появляется новая комета. Гаусс быстро и очень точно рассчитывает её орбиту. Начинает работу над комплексным анализом, открывает (но не публикует) теорему, позже переоткрытую Коши и Вейерштрассом: интеграл от аналитической функции по замкнутому контуру равен нулю.
1812 год: исследование гипергеометрического ряда, обобщающего разложение практически всех известных тогда функций.
Знаменитую комету «пожара Москвы» (1812) всюду наблюдают, пользуясь вычислениями Гаусса.
1815 год: публикует первое строгое доказательство основной теоремы алгебры.
1816—1855 годы
1821 год: в связи с работами по геодезии Гаусс начинает исторический цикл работ по теории поверхностей. В науку входит «гауссова кривизна». Положено начало дифференциальной геометрии. Именно результаты Гаусса вдохновили Римана на написание его классической диссертации о «римановой геометрии».
Итогом изысканий Гаусса была работа «Исследования относительно кривых поверхностей» (1822). В ней свободно использовались общие криволинейные координаты на поверхности. Гаусс далеко развил метод конформного отображения, которое в картографии сохраняет углы (но искажает расстояния); оно применяется также в аэро/гидродинамике и электростатике.
1824 год: избирается иностранным почётным членом Петербургской Академии наук.
1825 год: открывает гауссовы комплексные целые числа, строит для них теорию делимости и сравнений. Успешно применяет их для решения сравнений высоких степеней.
1831 год: умирает вторая жена, у Гаусса начинается тяжелейшая бессонница. В Гёттинген приезжает приглашённый по инициативе Гаусса 27-летний талантливый физик Вильгельм Вебер, с которым Гаусс познакомился в 1828 году, в гостях у Гумбольдта. Оба энтузиаста науки сдружились, несмотря на разницу в возрасте, и начинают цикл исследований электромагнетизма.
1832 год: «Теория биквадратичных вычетов». С помощью тех же целых комплексных гауссовых чисел доказываются важные арифметические теоремы не только для комплексных, но и для вещественных чисел. Здесь же Гаусс приводит геометрическую интерпретацию комплексных чисел, которая с этого момента становится общепринятой.
1833 год: Гаусс изобретает электрический телеграф и (вместе с Вебером) строит его действующую модель.
1837 год: Вебера увольняют за отказ принести присягу новому королю Ганновера. Гаусс вновь остаётся в одиночестве.
1839 год: 62-летний Гаусс овладевает русским языком и в письмах в Петербургскую Академию просил прислать ему русские журналы и книги, в частности «Капитанскую дочку» Пушкина. Предполагают, что это связано с работами Лобачевского. В 1842 году по рекомендации Гаусса Лобачевский избирается иностранным членом-корреспондентом Гёттингенского королевского общества.
Умер Гаусс 23 февраля 1855 года в Гёттингене.
Современники вспоминают Гаусса как жизнерадостного, дружелюбного человека, с отличным чувством юмора.
Увековечение памяти
В честь Гаусса названы:
С именем Гаусса связано множество теорем и научных терминов в математике, астрономии и физике.
Научная деятельность
С именем Гаусса связаны фундаментальные исследования почти во всех основных областях математики: алгебре, дифференциальной и неевклидовой геометрии, в математическом анализе, теории функций комплексного переменного, теории вероятностей, а также в астрономии, геодезии и механике. «В каждой области глубина проникновения в материал, смелость мысли и значительность результата были поражающими. Гаусса называли „королем математиков“» [2] (лат. Princeps mathematicorum ).
Несколько студентов, учеников Гаусса, стали выдающимися математиками, например: Риман, Дедекинд, Бессель, Мёбиус.
Алгебра
Гаусс дал первые строгие, даже по современным критериям, доказательства основной теоремы алгебры.
Он открыл кольцо целых комплексных гауссовых чисел, создал для них теорию делимости и с их помощью решил немало алгебраических проблем. Указал знакомую теперь всем геометрическую модель комплексных чисел и действий с ними.
Гаусс дал классическую теорию сравнений, открыл конечное поле вычетов по простому модулю, глубоко проник в свойства вычетов.
Геометрия
Гаусс впервые начал изучать внутреннюю геометрию поверхностей. Он открыл характеристику поверхности (гауссову кривизну), которая не изменяется при изгибаниях, тем самым заложив основы римановой геометрии. В 1827 году опубликовал полную теорию поверхностей. Доказал Theorema Egregium, основную теорему теории поверхностей. Труды Гаусса по дифференциальной геометрии дали мощный толчок развитию этой науки на весь XIX век. Попутно он создал новую науку — высшую геодезию.
Я прихожу всё более к убеждению, что необходимость нашей геометрии не может быть доказана, по крайней мере человеческим рассудком и для человеческого рассудка. Может быть, в другой жизни мы придем к взглядам на природу пространства, которые нам теперь недоступны. До сих пор геометрию приходится ставить не в один ранг с арифметикой, существующей чисто a priori, а скорее с механикой.
В его бумагах обнаружены содержательные заметки по тому предмету, что позже назвали топологией. Причём он предсказал фундаментальное значение этого предмета.
Древняя проблема построения правильных многоугольников с помощью циркуля и линейки была Гауссом окончательно решена (см. теорему Гаусса — Ванцеля).
Математический анализ
Гаусс продвинул теорию специальных функций, рядов, численные методы, решение задач математической физики. Создал математическую теорию потенциала.
Много и успешно занимался эллиптическими функциями, хотя почему-то ничего не публиковал на эту тему.
Астрономия
В астрономии Гаусс, в первую очередь, интересовался небесной механикой, изучал орбиты малых планет и их возмущения. Он предложил теорию учёта возмущений и неоднократно доказывал на практике её эффективность.
Другие достижения
Для минимизации влияния ошибок измерения Гаусс использовал свой метод наименьших квадратов, который сейчас повсеместно применяется в статистике. Хотя Гаусс не первый открыл распространённый в природе нормальный закон распределения, но он настолько тщательно его исследовал, что график распределения с тех пор часто называют гауссианой.
В физике Гаусс развил теорию капиллярности, теорию системы линз. Гаусс заложил основы математической теории электромагнетизма: первым ввёл понятие потенциала электрического поля, разработал систему электромагнитных единиц измерения СГС. Совместно с Вебером Гаусс сконструировал первый примитивный электрический телеграф.
Труды на русском языке
Примечания
Литература
Ссылки
Пиацци (1803) • Матьё (1807) • Гаусс (1810) • Бессель (1810) • Понд (1817) • Понс (1818) • Гершель (1825) • Эйри (1834) • Фай (1844) • Темпель (1861) • де ла Ру (1866) • Скиапарелли (1868) • Хаггинс (1870) • Свифт (1882) • Бигурдан (1883) • Баклунд (1886) • Бигурдан (1891) • Барнард (1892) • Бёрнхем (1904) • Блондло (1904) • Пикеринг (1906) • Босс (1911) • Белопольский (1918) • Рассел (1922) • Стойко (1930)
Полезное
Смотреть что такое «Гаусс, Карл Фридрих» в других словарях:
Гаусс Карл Фридрих — (Gauß) (1777 1855), немецкий математик, иностранный член корреспондент (1802) и иностранный почетный член (1824) Петербургской АН. Для творчества Гаусса характерна органическая связь между теоретической и прикладной математикой, широта… … Энциклопедический словарь
Гаусс Карл Фридрих — Гаусс (Gauss) Карл Фридрих (30.4.1777, Брауншвейг, 23.2.1855, Гёттинген), немецкий математик, внёсший фундаментальный вклад также в астрономию и геодезию. Родился в семье водопроводчика. С 1795 по 1798 учился в Гёттингенском университете. В 1799… … Большая советская энциклопедия
ГАУСС Карл Фридрих — (Gauss, Carl Friedrich) (1777 1855), немецкий математик, астроном и физик. Родился 30 апреля 1777 в Брауншвейге. Необыкновенные способности к математике и иностранным языкам проявились у Карла еще в детстве. Восьмилетний мальчик поразил учителя,… … Энциклопедия Кольера
Гаусс Карл Фридрих — … Википедия
Карл Фридрих Гаусс — Carl Friedrich Gauß Дата рождения: 30 апреля 1777 Место рождения: Брауншвейг Дата смерти: 23 февраля 1855 Место смерти … Википедия
ГАУСС (Gau?) Карл Фридрих — (1777 1855) немецкий математик, иностранный член корреспондент (1802) и иностранный почетный член (1824) Петербургской АН. Для творчества Гаусса характерна органическая связь между теоретической и прикладной математикой, широта проблематики.… … Большой Энциклопедический словарь
Карл Фридрих Гаусс — (1777 1855 гг.) математик …Мы должны признаться честно и откровенно, что в существенном мы нисколько не ушли в две тысячи лет дальше Эвклида. Такое откровенное и лишенное всяких обиняков признание кажется нам более соответствующим достоинству… … Сводная энциклопедия афоризмов
Карл Гаусс — Карл Фридрих Гаусс Carl Friedrich Gauß Дата рождения: 30 апреля 1777 Место рождения: Брауншвейг Дата смерти: 23 февраля 1855 Место смерти … Википедия
Фридрих-Вильгельм Бессель — Friedrich Wilhelm Bessel Дата рождения: 22 июля 1784 Место рождения: Минден, Вестфалия сейчас Германия Дата смерти: 17 марта 1 … Википедия
Фридрих Бессель — Фридрих Вильгельм Бессель Friedrich Wilhelm Bessel Дата рождения: 22 июля 1784 Место рождения: Минден, Вестфалия сейчас Германия Дата смерти: 17 марта 1 … Википедия
К. Гаусс
К. Гаусс
| Карл Фридрих Гаусс | |
| Carl Friedrich Gauß | |
 | |
| Дата рождения: | |
|---|---|
| Выдающиеся люди эпохи по странам | |
| Австрия | Иосиф II | Леопольд II | Мария Терезия |
| Франция | Пьер Бейль | Фонтенель | Шарль Луи Монтескьё | Франсуа Кёне | Вольтер | Жорж Луи Леклерк де Бюффон | Жан Жак Руссо | Дени Дидро | Гельвеций | Жан Д’Аламбер | Гольбах | Маркиз де Сад | Кондорсе | Лавуазье | Олимпия де Гугес | см. также: Французские энциклопедисты |
| Германия | Эрхард Вейгель | Готфрид Лейбниц | Фридрих II | Иммануил Кант | Готхольд Эфраим Лессинг | Томас Аббт | Иоганн Готфрид Гердер | Адам Вейсгаупт | Иоганн Вольфганг Гёте | Фридрих Шиллер | Карл Фридрих Гаусс | Мозес Мендельсон |
| Великобритания | Томас Гоббс | Джон Локк | Исаак Ньютон | Джозеф Аддисон | Ричард Стил | Сэмюэл Джонсон | Давид Юм | Адам Смит | Джон Уилкс | Эдмунд Бёрк | Эдуард Гиббон | Джеймс Босуэлл | Джереми Бентам | Мэри Уолстонкрафт | см. также: Шотландское Просвещение |
| Италия | Джамбаттиста Вико | Чезаре Беккариа |
| Нидерланды | Гуго Гроций | Бенедикт Спиноза |
| Польша | Станислав Конарский | Станислав Август Понятовский | Игнацы Красицкий | Гуго Коллонтай | Игнацы Потоцкий | Станислав Сташиц | Ян Снядецкий | Юлиан Урсын Немцевич | Анджей Снядецкий |
| Россия | Пётр I | Екатерина II | Екатерина Дашкова | Антиох Кантемир | Михаил Ломоносов | Николай Новиков | Александр Радищев | Иван Бецкой | Иван Шувалов | Михаил Щербатов |
| Испания | Гаспар Мельчор де Ховельянос | Николас Фернандес Моратин |
| США | Бенджамин Франклин | Дэвид Риттенхаус | Джон Адамс | Томас Пейн | Томас Джефферсон |
| Капитализм | Гражданские права | Критическое мышление | Деизм | Демократия | Эмпиризм | Просвещённый абсолютизм Свободные рынки | Гуманизм | Натурфилософия | Рациональность | Разум | Sapere aude | Наука | Секуляризация | Физиократия | Хаскала | |










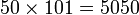 .
.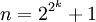 (числом Ферма). Этим открытием Гаусс очень дорожил и завещал изобразить на его могиле правильный 17-угольник, вписанный в круг.
(числом Ферма). Этим открытием Гаусс очень дорожил и завещал изобразить на его могиле правильный 17-угольник, вписанный в круг.

