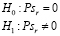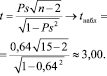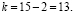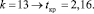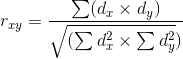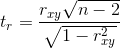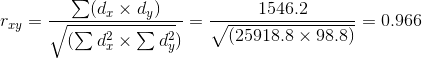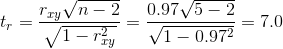Что определяют методом корреляции тест
Что определяют методом корреляции тест
Индивидуальные онлайн уроки: Отправьте запрос сейчас: irina@bodrenko.org
Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL)
Решение задач: по математике, IT, экономике, психологии
к лекции № 4 « Методы и модели корреляционно-регрессионного анализа »
« Математическое моделирование экономических систем »
1. Относительно типа соединения явлений различают следующие виды корреляции:
А) непосредственную корреляцию, косвенную корреляцию, ложную корреляцию;
Б) простую корреляцию, множественную корреляцию, частную корреляцию;
В) линейную корреляцию, нелинейную корреляцию.
2. Относительно формы связи явлений различают следующие виды корреляции:
А) непосредственную корреляцию, косвенную корреляцию, ложную корреляцию;
Б) простую корреляцию, множественную корреляцию, частную корреляцию;
В) линейную корреляцию, нелинейную корреляцию.
3. Относительно числа переменных различают следующие виды корреляции:
А) непосредственную корреляцию, косвенную корреляцию, ложную корреляцию;
Б) простую корреляцию, множественную корреляцию, частную корреляцию;
В) линейную корреляцию, нелинейную корреляцию.
4. В зависимости от характера корреляции различают следующие виды корреляции:
А) непосредственную корреляцию, косвенную корреляцию, ложную корреляцию;
Б) положительную корреляцию, отрицательную корреляцию, нулевую корреляцию;
В) линейную корреляцию, нелинейную корреляцию.
5. Для нахождения уравнения прямой регрессии применяется:
В) метод наименьших квадратов.
6. Проверка коэффициентов регрессии на статистическую значимость проводится:
А) по критерию Стьюдента;
Б) по критерию Фишера;
7. Мультиколлинеарность факторов модели – это:
А) попарная корреляционная зависимость между факторами ;
8. Для устранения мультиколлинеарности факторов в корреляционно-регрессионном анализе используется:
А) метод наименьших квадратов;
Б) метод исключения переменных;
9. Целесообразность исключения факторов из модели исследуется с помощью коэффициента:
Б) парной корреляции;
10. Анализ факторов на мультиколлинеарностъ проводится с помощью коэффициентов:
Что определяют методом корреляции тест
Как неоднократно отмечалось, для статистического вывода о наличии или отсутствии корреляционной связи между исследуемыми переменными необходимо произвести проверку значимости выборочного коэффициента корреляции. В связи с тем что надежность статистических характеристик, в том числе и коэффициента корреляции, зависит от объема выборки, может сложиться такая ситуация, когда величина коэффициента корреляции будет целиком обусловлена случайными колебаниями в выборке, на основании которой он вычислен. При существенной связи между переменными коэффициент корреляции должен значимо отличаться от нуля. Если корреляционная связь между исследуемыми переменными отсутствует, то коэффициент корреляции генеральной совокупности ρ равен нулю [9].
Как всякая статистическая характеристика, выборочный коэффициент корреляции является случайной величиной, т.е. его значения случайно рассеиваются вокруг одноименного параметра генеральной совокупности (истинного значения коэффициента корреляции) [1].
При отсутствии корреляционной связи между переменными у и х коэффициент корре ляции в генеральной совокупности равен нулю. Но из-за случайного характера рассеяния принципиально возможны ситуации, когда некоторые коэффициенты корреляции, вычисленные по выборкам из этой совокупности, будут отличны от нуля [5].
Процедура проверки значимости начинается с формулировки нулевой гипотезы H0. В общем виде она заключается в том, что между параметром выборки и параметром гене ральной совокупности нет каких-либо существенных различий. Альтернативная гипотеза H1 состоит в том, что между этими параметрами имеются существенные различия. Например, при проверке наличия корреляции в генеральной совокупности нулевая гипотеза заключается в том, что истинный коэффициент корреляции равен нулю 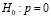
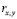
При проверке значимости исследователь устанавливает уровень значимости α, который дает определенную практическую уверенность в том, что ошибочные заключения будут сделаны только в очень редких случаях. Уровень значимости выражает вероятность того, что нулевая гипотеза Н0 отвергается в то время, когда она в действительности верна. Ясно, что имеет смысл выбирать эту вероятность как можно меньшей [2].
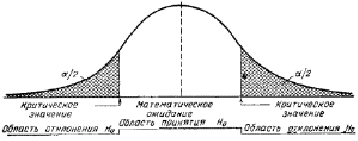
Пусть известно распределение выборочной характеристики, являющейся несмещенной оценкой параметра генеральной совокупности. Выбранному уровню значимости α соответствуют под кривой этого распределения заштрихованные площади (см. рис. 1). Незаштрихованная площадь под кривой распределения определяет вероятность
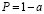
Границы отрезков на оси абсцисс под заштрихованными площадями называют критическими значениями, а сами отрезки образуют критическую область, или область отклонения гипотезы [3].
Когда же надо убедиться в том, что одна величина в среднем строго больше или мень ше другой, используется односторонняя критическая область. Если распределение выборочной характеристики симметрично, то уровень значимости двусторонней критической области равен α, а односторонней 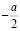
Рис. 1 Проверка нулевой гипотезы H0
Проверяя значимость коэффициента парной корреляции, устанавливают наличие или отсутствие корреляционной связи между исследуемыми явлениями. При отсутствии связи коэффициент корреляции генеральной совокупности равен нулю (p=0). Процедура проверки начинается с формулировки нулевой и альтернативной гипотез [8]:
Н0: различие между выборочным коэффициентом корреляции r и ρ = 0 незначимо,
Н1: различие между r и p=0 значимо, и следовательно, между переменными у и х имеется существенная связь. Из альтернативной гипотезы следует, что нужно воспользоваться двусторонней критической областью.
Выборочный коэффициент корреляции при определенных предпосылках связан со случайной величиной t, подчиняющейся распределению Стьюдента с 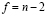
Вычисленная по результатам выборки статистика
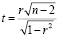
сравнивается с критическим значением, определяемым по таблице распределения Стьюдента при заданном уровне значимости α и 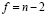
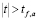
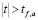
то нулевая гипотеза на уровне значимости α принимается. Отклонение значения r от 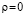
Рассмотрим на конкретном примере проверку гипотезы о значимости выборочного коэффициента корреляции.
Для 15 пар порядковых переменных (x, y) был вычислен коэффициент корреляции Спирмена, который оказался равным 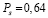
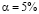
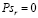
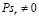
Найдем наблюдаемое значение критерия:
Найдем значения границ двусторонней критической области из условия, что при малых объемах выборок критерий t распределен (при справедливости нулевой гипотезы) по закону распределения Стьюдента с числом степеней свободы
На основе таблицы «Критические точки распределения Стьюдента» найдем границы двусторонней критической области на основе
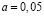
Полученные результаты покажем графически (рис. 2).
Поскольку наблюдаемое значение критерия попало в критическую область, то следует отклонить нулевую гипотезу в пользу альтернативной гипотезы. Это означает, что коэффициент ранговой корреляции значим: между двумя порядковыми случайными величинами X и Y в генеральной совокупности имеется значимая связь, которая говорит о наличии связи этих двух случайных величин.
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
КРИТЕРИЙ КОРРЕЛЯЦИИ ПИРСОНА
– это метод параметрической статистики, позволяющий определить наличие или отсутствие линейной связи между двумя количественными показателями, а также оценить ее тесноту и статистическую значимость. Другими словами, критерий корреляции Пирсона позволяет определить, изменяется ли (возрастает или уменьшается) один показатель в ответ на изменения другого? В статистических расчетах и выводах коэффициент корреляции обычно обозначается как rxy или Rxy.
1. История разработки критерия корреляции
Критерий корреляции Пирсона был разработан командой британских ученых во главе с Карлом Пирсоном (1857-1936) в 90-х годах 19-го века, для упрощения анализа ковариации двух случайных величин. Помимо Карла Пирсона над критерием корреляции Пирсона работали также Фрэнсис Эджуорт и Рафаэль Уэлдон.
2. Для чего используется критерий корреляции Пирсона?
Критерий корреляции Пирсона позволяет определить, какова теснота (или сила) корреляционной связи между двумя показателями, измеренными в количественной шкале. При помощи дополнительных расчетов можно также определить, насколько статистически значима выявленная связь.
Например, при помощи критерия корреляции Пирсона можно ответить на вопрос о наличии связи между температурой тела и содержанием лейкоцитов в крови при острых респираторных инфекциях, между ростом и весом пациента, между содержанием в питьевой воде фтора и заболеваемостью населения кариесом.
3. Условия и ограничения применения критерия хи-квадрат Пирсона
Например, рост ребенка зависит от его возраста, то есть чем старше ребенок, тем он выше. Если мы возьмем двух детей разного возраста, то с высокой долей вероятности рост старшего ребенка будет больше, чем у младшего. Данное явление и называется зависимостью, подразумевающей причинно-следственную связь между показателями. Разумеется, между ними имеется и корреляционная связь, означающая, что изменения одного показателя сопровождаются изменениями другого показателя.
В другой ситуации рассмотрим связь роста ребенка и частоты сердечных сокращений (ЧСС). Как известно, обе эти величины напрямую зависят от возраста, поэтому в большинстве случаев дети большего роста (а значит и более старшего возраста) будут иметь меньшие значения ЧСС. То есть, корреляционная связь будет наблюдаться и может иметь достаточно высокую тесноту. Однако, если мы возьмем детей одного возраста, но разного роста, то, скорее всего, ЧСС у них будет различаться несущественно, в связи с чем можно сделать вывод о независимости ЧСС от роста.
Приведенный пример показывает, как важно различать фундаментальные в статистике понятия связи и зависимости показателей для построения верных выводов.
4. Как рассчитать коэффициента корреляции Пирсона?
Расчет коэффициента корреляции Пирсона производится по следующей формуле:
5. Как интерпретировать значение коэффициента корреляции Пирсона?
Более точную оценку силы корреляционной связи можно получить, если воспользоваться таблицей Чеддока:
| Абсолютное значение rxy | Теснота (сила) корреляционной связи |
| менее 0.3 | слабая |
| от 0.3 до 0.5 | умеренная |
| от 0.5 до 0.7 | заметная |
| от 0.7 до 0.9 | высокая |
| более 0.9 | весьма высокая |
Оценка статистической значимости коэффициента корреляции rxy осуществляется при помощи t-критерия, рассчитываемого по следующей формуле:
Полученное значение tr сравнивается с критическим значением при определенном уровне значимости и числе степеней свободы n-2. Если tr превышает tкрит, то делается вывод о статистической значимости выявленной корреляционной связи.
6. Пример расчета коэффициента корреляции Пирсона
Целью исследования явилось выявление, определение тесноты и статистической значимости корреляционной связи между двумя количественными показателями: уровнем тестостерона в крови (X) и процентом мышечной массы в теле (Y). Исходные данные для выборки, состоящей из 5 исследуемых (n = 5), сведены в таблице:
Σ(X) = 951 + 874 + 957 + 1084 + 903 = 4769
Σ(Y) = 83 + 76 + 84 + 89 + 79 = 441
Mx = Σ(X) / n = 4769 / 5 = 953.8
My = Σ(Y) / n = 441 / 5 = 82.2
Корреляции в дипломных работах по психологии
Термин «корреляция» активно используется в гуманитарных науках, медицине; часто мелькает в СМИ. Ключевую роль корреляции играют в психологии. В частности, расчет корреляций выступает важным этапом реализации эмпирического исследования при написании ВКР по психологии.
В этой статье мы простым языком объясним суть корреляционной связи, виды корреляций, способы расчета, особенности использования корреляции в психологических исследованиях, а также при написании дипломных работ по психологии.
Что такое корреляция
Корреляция – это связь. Но не любая. В чем же ее особенность? Рассмотрим на примере.
Представьте, что вы едете на автомобиле. Вы нажимаете педаль газа – машина едет быстрее. Вы сбавляете газ – авто замедляет ход. Даже не знакомый с устройством автомобиля человек скажет: «Между педалью газа и скоростью машины есть прямая связь: чем сильнее нажата педаль, тем скорость выше».
Это зависимость функциональная – скорость выступает прямой функцией педали газа. Специалист объяснит, что педаль управляет подачей топлива в цилиндры, где происходит сжигание смеси, что ведет к повышению мощности на вал и т.д. Это связь жесткая, детерминированная, не допускающая исключений (при условии, что машина исправна).
Теперь представьте, что вы директор фирмы, сотрудники которой продают товары. Вы решаете повысить продажи за счет повышения окладов работников. Вы повышаете зарплату на 10%, и продажи в среднем по фирме растут. Через время повышаете еще на 10%, и опять рост. Затем еще на 5%, и опять есть эффект. Напрашивается вывод – между продажами фирмы и окладом сотрудников есть прямая зависимость – чем выше оклады, тем выше продажи организации. Такая же это связь, как между педалью газа и скоростью авто? В чем ключевое отличие?
Правильно, между окладом и продажами заисимость не жесткая. Это значит, что у кого-то из сотрудников продажи могли даже снизиться, невзирая на рост оклада. У кого-то остаться неизменными. Но в среднем по фирме продажи выросли, и мы говорим – связь продаж и оклада сотрудников есть, и она корреляционная.
В основе функциональной связи (педаль газа – скорость) лежит физический закон. В основе корреляционной связи (продажи – оклад) находится простая согласованность изменения двух показателей. Никакого закона (в физическом понимании этого слова) за корреляцией нет. Есть лишь вероятностная (стохастическая) закономерность.
Численное выражение корреляционной зависимости
Итак, корреляционная связь отражает зависимость между явлениями. Если эти явления можно измерить, то она получает численное выражение.
Полученное число называется коэффициентом корреляции. Для его правильной интерпретации важно учитывать следующее:
Прямая и обратная
Сильная и слабая
Чем ниже численное значение коэффициента, тем взаимосвязь между явлениями и показателями меньше.
Рассмотрим пример. Взяли 10 студентов и измерили у них уровень интеллекта (IQ) и успеваемость за семестр. Расположили эти данные в виде двух столбцов.
Испытуемый
Успеваемость (баллы)
Посмотрите внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. Но также растет и уровень успеваемости. Из любых двух студентов успеваемость будет выше у того, у кого выше IQ. И никаких исключений из этого правила не будет.
Перед нами пример полного, 100%-но согласованного изменения двух показателей в группе. И это пример максимально возможной положительной взаимосвязи. То есть, корреляционная зависимость между интеллектом и успеваемостью равна 1.
Рассмотрим другой пример. У этих же 10-ти студентов с помощью опроса оценили, в какой мере они ощущают себя успешными в общении с противоположным полом (по шкале от 1 до 10).
Испытуемый
Успех в общении с противоположным полом (баллы)
Смотрим внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. При этом в последнем столбце последовательно снижается уровень успешности общения с противоположным полом. Из любых двух студентов успех общения с противоположным полом будет выше у того, у кого IQ ниже. И никаких исключений из этого правила не будет.
А как понять смысл корреляции равной нулю (0)? Это значит, связи между показателями нет. Еще раз вернемся к нашим студентам и рассмотрим еще один измеренный у них показатель – длину прыжка с места.
Испытуемый
Длина прыжка с места (м)
Не наблюдается никакой согласованности между изменением IQ от человека к человеку и длинной прыжка. Это и свидетельствует об отсутствии корреляции. Коэффициент корреляции IQ и длины прыжка с места у студентов равен 0.
Мы рассмотрели крайние случаи. В реальных измерениях коэффициенты редко бывают равны точно 1 или 0. При этом принята следующая шкала:
Приведенная градация дает очень приблизительные оценки и в таком виде редко используются в исследованиях.
Чаще используются градации коэффициентов по уровням значимости. В этом случае реально полученный коэффициент может быть значимым или не значимым. Определить это можно, сравнив его значение с критическим значением коэффициента корреляции, взятым из специальной таблицы. Причем эти критические значения зависят от численности выборки (чем больше объем, тем ниже критическое значение).
Корреляционный анализ в психологии
Корреляционный метод выступает одним из основных в психологических исследованиях. И это не случайно, ведь психология стремится быть точной наукой. Получается ли?
В чем особенность законов в точных науках. Например, закон тяготения в физике действует без исключений: чем больше масса тела, тем сильнее оно притягивает другие тела. Этот физический закон отражает связь массы тела и силы притяжения.
Пример исследования на студентах из предыдущего раздела хорошо иллюстрирует использование корреляций в психологии:
Вот как могли выглядеть краткие выводы по результатам придуманного исследования на студентах:
Таким образом, уровень интеллекта студентов выступает позитивным фактором их академической успеваемости, в то же время негативно сказываясь на отношениях с противоположным полом и не оказывая значимого влияния на спортивные успехи, в частности, способность к прыгать с места.
Как видим, интеллект помогает студентам учиться, но мешает строить отношения с противоположным полом. При этом не влияет на их спортивные успехи.
Неоднозначное влияние интеллекта на личность и деятельность студентов отражает сложность этого феномена в структуре личностных особенностей и важность продолжения исследований в этом направлении. В частности, представляется важным провести анализ взаимосвязей интеллекта с психологическими особенностями и деятельностью студентов с учетом их пола.
Коэффициенты Пирсона и Спирмена
Рассмотрим два метода расчета.
Коэффициент Пирсона – это особый метод расчета взаимосвязи показателей между выраженностью численных значений в одной группе. Очень упрощенно он сводится к следующему:
Коэффициент ранговой корреляции Спирмена рассчитывается похожим образом:
В случае Пирсона расчет шел с использованием среднего значения. Следовательно, случайные выбросы данных (существенное отличие от среднего), например, из-за ошибки обработки или недостоверных ответов могут существенно исказить результат.
В случае Спирмена абсолютные значения данных не играют роли, так как учитывается только их взаимное расположение по отношению друг к другу (ранги). То есть, выбросы данных или другие неточности не окажут серьезного влияния на конечный результат.
Если результаты тестирования корректны, то различия коэффициентов Пирсона и Спирмена незначительны, при этом коэффициент Пирсона показывает более точное значение взаимосвязи данных.
Как рассчитать коэффициент корреляции
Коэффициенты Пирсона и Спирмена можно рассчитать вручную. Это может понадобиться при углубленном изучении статистических методов.
Однако в большинстве случаев при решении прикладных задач, в том числе и в психологии, можно проводить расчеты с помощью специальных программ.
Расчет с помощью электронных таблиц Microsoft Excel
Вернемся опять к примеру со студентами и рассмотрим данные об уровне их интеллекта и длине прыжка с места. Занесем эти данные (два столбца) в таблицу Excel.
Переместив курсор в пустую ячейку, нажмем опцию «Вставить функцию» и выберем «КОРРЕЛ» из раздела «Статистические».
Формат этой функции предполагает выделение двух массивов данных: КОРРЕЛ (массив 1; массив»). Выделяем соответственно столбик с IQ и длиной прыжков.
В таблицах Excel реализована формула расчета только коэффициента Пирсона.
Расчет с помощью программы STATISTICA
Заносим данные по интеллекту и длине прыжка в поле исходных данных. Далее выбираем опцию «Непараметрические критерии», «Спирмена». Выделяем параметры для расчета и получаем следующий результат.
Как видно, расчет дал результат 0,024, что отличается от результата по Пирсону – 0,038, полученной выше с помощью Excel. Однако различия незначительны.
Использование корреляционного анализа в дипломных работах по психологии (пример)
Большинство тем выпускных квалификационных работ по психологии (дипломов, курсовых, магистерских) предполагают проведение корреляционного исследования (остальные связаны с выявлением различий психологических показателей в разных группах).
Сам термин «корреляция» в названиях тем звучит редко – он скрывается за следующими формулировками:
Рассмотрим кратко этапы его проведения при написании дипломной работы по психологии на тему: «Взаимосвязь личностной тревожности и агрессивности у подростков».
1. Для расчета необходимы сырые данные, в качестве которых обычно выступают результаты тестирования испытуемых. Они заносятся в сводную таблицу и помещаются в приложение. Эта таблица устроена следующим образом: