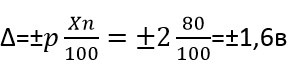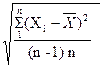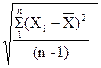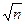Что определяет точность измерения
ТОЧНОСТЬ ИЗМЕРЕНИЙ
Смотреть что такое «ТОЧНОСТЬ ИЗМЕРЕНИЙ» в других словарях:
Точность измерений — Качество измерений, отражающее близость их результатов к истинному значению измеряемой величины Источник: ГОСТ 24846 81: Грунты. Методы измерения деформаций оснований зданий и сооружений … Словарь-справочник терминов нормативно-технической документации
точность измерений — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN accuracy of measurements … Справочник технического переводчика
Точность измерений — помощью так называемых измерительных приборов постоянно возрастает с ростом науки (Измерения; Единицы мер абсолютные системы). Она зависит теперь не только от тщательного приготовления приборов, но еще от нахождения новых принципов измерений. Так … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
точность измерений — поверка. поверять. прибор врет. см. показывать время … Идеографический словарь русского языка
ГОСТ Р ЕН 306-2011: Теплообменники. Измерения и точность измерений при определении мощности — Терминология ГОСТ Р ЕН 306 2011: Теплообменники. Измерения и точность измерений при определении мощности: 3.31 величина воздействия: Величина, не являющаяся предметом измерения, но способная влиять на получаемый результат. Определения термина из… … Словарь-справочник терминов нормативно-технической документации
точность результата измерений — точность измерений Одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения. Примечание. Считают, что чем меньше погрешность измерения, тем больше его точность. [РМГ 29 99] Тематики метрология,… … Справочник технического переводчика
точность — 3.1.1 точность (accuracy): Степень близости результата измерений к принятому опорному значению. Примечание Термин «точность», когда он относится к серии результатов измерений, включает сочетание случайных составляющих и общей систематической… … Словарь-справочник терминов нормативно-технической документации
Точность — средства измерений степень совпадения показаний измерительного прибора с истинным значением измеряемой величины. Чем меньше разница, тем больше точность прибора. Точность эталона или меры характеризуется погрешностью или степенью… … Википедия
точность — Степень близости результата измерений к принятому опорному значению. Примечание. Термин «точность», когда он относится к серии результатов измерений (испытаний), включает сочетание случайных составляющих и общей систематической… … Справочник технического переводчика
точность средства измерений — точность Характеристика качества средства измерений, отражающая близость его погрешности к нулю. Примечание. Считается, что чем меньше погрешность, тем точнее средство измерений. [РМГ 29 99] Тематики метрология, основные понятия Синонимы точность … Справочник технического переводчика
Содержание:
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Пример:
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.
Абсолютная погрешность измерения ∆ (ДЕЛЬТА)
Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать
Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.
Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: 

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
На точность измерения влияет много факторов, в частности:
Все это необходимо учитывать при проведении измерений.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.
Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.
Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.
Как определяют единицы длины и времени
В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.
Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).
Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.
Можно ли расстояние измерять годами
Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!
Что надо знать об измерительных приборах
Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?
На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.
Цена деления — это значение наименьшего деления шкалы прибора.
Как определить цену деления шкалы? Для этого необходимо:
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:
Цена деления шкалы мензурки 2:
А какими линейкой и мензуркой можно измерить точнее?
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.
Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.
Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.
Главные выводы:
Для любознательных:
В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.
Пример решения задачи
Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.
Решение:
1) Цена деления нижней шкалы:
Цена деления средней шкалы:
Цена деления верхней шкалы:
2) Определенный но нижней шкале с точностью до 10° 

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Что нужно знать о классе точности измерительного прибора?
Измерительные приборы: вольтметры, амперметры, токовые клещи, осциллографы и другие — это устройства, предназначенные для определения искомых величин в заданном диапазоне, каждый из них имеет свою точность, причем устройства, измеряющие одну и ту же величину, в зависимости от модели, могут отличаться по точности и классу.
В каких-то ситуациях достаточно просто определить значение, например, вольтаж батарейки, а в других необходимо выполнить многократное повторение измерений высокоточными приборами для получения максимально достоверного результата, так в чем отличие таких измерительных устройств, что означает класс точности, сколько их бывает, как его определить и многое другое читайте далее в нашей статье.
Что такое класс точности
Определение: «Класс точности измерения — это общая характеристика точности средства измерения, определяемая пределами допустимых основных и дополнительных погрешностей, а также другими факторами, влияющими на нее».
Сам по себе класс не является постоянной величиной измерения, потому что само измерение зачастую зависит от множества переменных: места измерения, температуры, влажности и других факторов, класс позволяет определить лишь только в каком диапазоне относительных погрешностей работает данный прибор.
Чтобы заранее оценить погрешность, которую измерит устройство, также могут использоваться нормативные справочные значения.
Относительная погрешность — это отношение абсолютной погрешности к модулю действительного приближенного показателя полученного значения, измеряется в %.
Абсолютная погрешность рассчитывается следующим образом:
∆=±a или ∆=(a+bx)
x – число делений, нормирующее значение величины
a, b – положительные числа, не зависящие от х
Абсолютная и приведенная погрешность рассчитывается по следующим формулам, см. таблицу ниже
Какие классы точности бывают, как обозначаются
Как мы уже успели выяснить, интервал погрешности определяется классом точности. Данная величина рассчитывается, устанавливается ГОСТом и техническими условиями. В зависимости от заданной погрешность, бывает: абсолютная, приведенная, относительная, см. таблицу ниже
Согласно ГОСТ 8.401-80 в системе СИ классы точности обычно помечается латинской буквой, часто с добавлением индекса, отмеченного цифрой. Чем меньше погрешность, соответственно, меньше цифра и буквенное значение выше по алфавиту, тем более высокая точность.
Класс точности обозначается на корпусе устройства в виде числа обведенного в кружок, обозначает диапазон погрешностей измерений в процентах. Например, цифра ② означает относительную погрешность ±2%. Если рядом со знаком присутствует значок в виде галочки, это значит, что длина шкалы используется в качестве вспомогательного определения погрешности.
Каким ГОСТом регламентируется точность приборов?
ГОСТ 8.401-80 «Классы точности средств измерений» общие требования. Нормативным документом устанавливаются общие положения классификации точностей измерительных приборов.
Как определить класс точности электроизмерительного прибора, формулы расчета
Чтобы определить класс точности, необходимо взглянуть на его корпус или инструкцию пользователя, в ней вы можете увидеть цифру, обведенную в круг, например, ① это означает, что ваш прибор измеряет величину с относительной погрешностью ±1%.
Но что делать если известна относительная погрешность и необходимо рассчитать класс точности, например, амперметра, вольтметра и т.д. Рассмотрим на примере амперметра: известна ∆x=базовая (абсолютная) погрешность 0,025 (см. в инструкции), количество делений х=12
Находим относительную погрешность:
Y= 100×0,025/12=0,208 или 2,08%
(вывод: класс точности – 2,5).
Следует отметить, что погрешность неравномерна на всем диапазоне шкалы, измеряя малую величину вы можете получить наибольшую неточность и с увеличением искомой величины она уменьшается, для примера рассмотрим следующий вариант:
Вольтметр с классом p=±2, верхний предел показаний прибора Xn=80В, число делений x=12
Предел абсолютной допустимой погрешности:
Относительная погрешность одного деления:
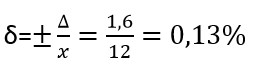
Если вам необходимо выполнить более подробный расчет, смотрите ГОСТ 8.401-80 п.3.2.6.
Поверка приборов, для чего она нужна
Все измерительные приборы измеряют с некой погрешностью, класс точности говорит лишь о том, в каком диапазоне она находится. Бывают случаи, когда диапазон погрешности незаметно увеличивается, и мы начинаем замечать, что измеритель «по-простому» начинает врать. В таких случаях помогает поверка.
Это процесс измерения эталонной величины в идеальных условиях прибором, обычно проводится метрологической службой или в метрологическом отделе предприятия производителя.
Существует первичная и периодическая, первичную проверку проводят после выпуска изделия и выдают сертификат, периодическую проводят не реже чем раз в год, для ответственных приборов чаще.
Поэтому если вы сомневаетесь в правильности работы устройства, вам следует провести его поверку в ближайшей метрологической службе, потому что измеритель может врать как в меньшую, так и в большую сторону.
Как легко проверить потребление электроэнергии в квартире, можете узнать в нашей статье.
Видео на тему относительная погрешность прибора
Заключение
Класс точности является важным показателем для каждого прибора, при выборе всегда обращайте внимание на него. Если вам нужен, например, электрический счетчик, важно чтобы он измерял потребление энергии с максимальной точностью, благодаря этому за весь период эксплуатации, вы сможете сэкономить приличную сумму средств.
Но, а если вам необходимо просто периодически проверять напряжение в розетке, для этого не стоит переплачивать за дорогостоящую покупку.
Определение точности измерений
3.4.1 Понятие погрешности измерения
При практическом использовании тех или иных результатов измерений важно оценить их точность. Термин «точность измерений», т. е. степень приближения результатов измерения к некоторому истинному значению, не имеет строгого определения и используется для качественного сравнения измерительных операций. Для количественной оценки применяется понятие «погрешность измерений» (чем меньше погрешность, тем выше точность).
Погрешность измерений зависит в первую очередь от погрешностей СИ, а также от условий, в которых проводится измерение, от экспериментальной ошибки методики и субъективных особенностей человека в случаях, где он непосредственно участвует в измерениях. Поэтому можно говорить о нескольких составляющих погрешности измерений или о ее суммарной погрешности.
Количество факторов, влияющих на точность измерения, достаточно велико, и любая классификация погрешностей измерения (рисунок.15) в известной мере условна, так как различные погрешности в зависимости от условий измерительного процесса проявляются в разных группах.
Рисунок 15 – Классификация погрешностей измерения
3.4.2 Виды погрешностей
Как указывалось выше, погрешность измерения – это отклонение результата измерения Х от истинного Хи значения измеряемой величины. При этом вместо истинного значения физической величины Хи используют ее действительное значение Хд.
В зависимости от формы выражения различают абсолютную, относительную и приведенную погрешности измерения.
Относительная погрешность – это погрешность средства измерений, выраженная отношением абсолютной погрешности средства измерений к результату измерений или действительному значению измеряемой физической величины. Она определяется как отношение δ = ±(Δ/Хд)·100%.
Приведенная погрешность – выраженное в % отношении измеряемой величины к значению абсолютной погрешности прибора, которое соответствует конечной отметке шкалы этого прибора, называют относительной приведенной погрешностью прибора.
В качестве нормирующего значения (ΧN) используют диапазон измерений прибора. Главная предельно допустимая приведенная погрешность прибора обуславливает класс точности этого прибора. Классы точности: 0,05; 0,1; 0,2;1,0; 1,5; 2,5; 4,0.Так, приборы класса точности 2,5 имеют допустимую приведенную погрешность 2,5%. Сведения о погрешности прибора, как правило, указывают на его шкале, а также в паспорте прибора. Они позволяют осуществить подходящий правильный подбор в зависимости от условий эксплуатации и определённо помогают правильно использовать прибор при выполнении измерений.
Методами теории вероятностей установлено, что в качестве действительного значения результата при многократных измерениях параметра, изменяющегося случайным образом, выступает среднее арифметическое значение X:
Величина `X, полученная в одной серии измерений, является случайным приближением к Хи. Для оценки ее возможных отклонений от Хи определяют оценку среднего квадратического отклонения от среднего арифметического:
S(`X)=
Для оценки рассеяния отдельных результатов измерения Xi относительно среднего арифметического `X определяют выборочное среднее квадратическое отклонение:
σ =
Эти формулы соответствуют центральной предельной теореме теории вероятностей, согласно которой среднее арифметическое из ряда измерений всегда имеет меньшую погрешность, чем погрешность каждого определенного измерения:
S(`X)= σ /
Эта формула отражает фундаментальный закон теории погрешностей. Из него следует, что если необходимо повысить точность результата (при исключенной систематической погрешности) в 2 раза, то число измерений нужно увеличить в 4 раза; если точность требуется увеличить в 3 раза, то число измерений увеличивают в 9 раз и т.д.
Нужно четко разграничивать применение величин S и σ: первая используется при оценке погрешностей окончательного результата, а вторая – при оценке погрешности метода измерения.
В зависимости от характера проявления, причин возникновения и возможностей устранения различают систематическую и случайную погрешности измерений, а также грубые погрешности (промахи).
Систематическая погрешность – это составляющая погрешности, принимаемая за постоянную или закономерно изменяющуюся при повторных измерениях одного и того же параметра. Как правило, считают, что систематические погрешности могут быть обнаружены и исключены. Однако в реальных условиях полностью исключить эти погрешности невозможно. Всегда остаются какие-то неисключенные остатки, которые нужно учитывать, чтобы оценить их границы. Это и будет систематическая погрешность измерения.
Случайная погрешность – это составляющая погрешности, изменяющаяся в тех же условиях измерения случайным образом. Значение случайной погрешности заранее неизвестно, она возникает из-за множества не уточненных факторов. Исключить из результатов случайные погрешности нельзя, но их влияние может быть уменьшено путем статистической обработки результатов измерений.
Случайная и систематическая составляющие погрешности измерения проявляются одновременно, так что при их независимости их общая погрешность равна сумме погрешностей. В принципе систематическая погрешность тоже случайна и указанное деление обусловлено лишь установившимися традициями обработки и представления результатов измерения.
В отличие от случайной погрешности, выявляемой в целом, вне зависимости от ее источников, систематическая погрешность рассматривается по составляющим в зависимости от источников ее возникновения. Различают субъективную, методическую и инструментальную составляющие систематической погрешности.
Субъективная составляющая погрешности связана с индивидуальными особенностями оператора. Как правило, эта погрешность возникает из-за ошибок в отсчете показаний и неверных навыков оператора. В основном же систематическая погрешность возникает из-за методической и инструментальной составляющих.
Методическая составляющая погрешности обусловлена несовершенством метода измерения, приемами использования средств измерения, некорректностью расчетных формул и округления результатов.
Инструментальная составляющая возникает из-за собственно погрешности средств измерения, определяемой классом его точности, влиянием средств измерения на объект измерения и ограниченной разрешающей способности средств измерения.
Целесообразность разделения систематической погрешности на методическую и инструментальную составляющие объясняется следующим:
для повышения точности измерений можно выделить лимитирующие факторы и, следовательно, принять решение либо об усовершенствовании методики, либо о выборе более точных средств измерения;
появляется возможность определить составляющую общей погрешности, увеличивающейся либо со временем, либо под влиянием внешних факторов, и, следовательно, целенаправленно осуществлять периодические поверки и аттестации;
инструментальная составляющая может быть оценена доразработки методики, а потенциальные точностные возможности выбранного метода определит только методическая составляющая.
Грубые погрешности (промахи) возникают из-за ошибочных действий оператора, неисправности средств измерения или резких изменений условий измерений. Как правило, грубые погрешности выявляются в результате статистической обработки результатов измерений при помощи специальных критериев.
3.4.3 Показатели качества измерений и испытаний
Единство измерений, однако, не может быть обеспечено только знанием погрешностей. При проведении измерений также важно знать показатели качества измерений. Под качеством измерений понимают совокупность свойств, обусловливающих получение результатов с требуемыми точностными характеристиками в необходимом виде и в установленные сроки.
Качество измерений характеризуется такими показателями, как точность, правильность и достоверность. Эти показатели должны определяться по оценкам, к которым предъявляются требования состоятельности, несмещенности и эффективности. Причем, в отличие от числовых характеристик, оценки являются случайными величинами, значение которых зависит от числа наблюдений n.
Состоятельной называют оценку, которая при n→ ∞ сводится по вероятности к оцениваемой величине.
Несмещенной называется оценка, математическое ожидание которой равно оцениваемой величине.
Эффективной называют такую оценку, которая имеет наименьшую дисперсию σ 2 = min.
Точность измерений определяется близостью к нулю погрешности результата измерения. Количественно точность может быть выражена обратной величиной модуля относительной погрешности, определенной в долях.
Правильность измерений определяется близостью к нулю систематической погрешности, т.е. результат «исправлен» на величину систематической погрешности.
Достоверность измерений определяется степенью доверия к результату и характеризуется вероятностью того, что истинное значение измеряемой величины лежит в указанных окрестностях действительного. Эти вероятности называют доверительными, а окрестности – доверительным интервалом с доверительными границами.
Доверительным интервалом от – Δд до + Δд называют интервал значений случайной погрешности, который с заданной доверительной вероятностью Рд накрывает истинное значение измеряемой величины:
При малом числе измерений (n 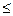
Поэтому при малом числе измерений используют распределение Стьюдента (предложенное английским статистиком Госсетом, публиковавшимся под псевдонимом «студент»), которое обеспечивает возможность определения доверительных интервалов при ограниченном числе измерений.
Границы доверительного интервала при этом определяются по формуле
Δд = t·S( 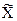
где t – коэффициент распределения Стьюдента, зависящий от задаваемой доверительной вероятности Рд и числа измерений n.
При увеличении числа наблюдений n распределение Стьюдента быстро приближается к нормальному распределению и совпадает с ним уже при n ≥30.
Следует отметить, что результаты измерений, не обладающие достоверностью, т. е. степенью уверенности в их правильности, не представляют ценности. К примеру, датчик измерительной схемы может иметь весьма высокие метрологические характеристики, но влияние погрешностей от его установки, внешних условий, методов регистрации и обработки сигналов приведет к большой конечной погрешности измерений.
При проведении испытаний их качество, наряду с такими показателями, как точность, правильность и достоверность, характеризуется также сходимостью и воспроизводимостью результатов.
Очевидно, что два испытания одного и того же объекта одинаковым методом не дают идентичных результатов. Объективной мерой их могут служить статистически обоснованные оценки ожидаемой близости результатов двух или более испытаний, полученных при строгом соблюдении их методики. В качестве таких статистических оценок согласованности результатов испытаний и принимаются сходимость и воспроизводимость.
Сходимость – это близость результатов двух испытаний, полученных одним методом, на идентичных установках, в одной лаборатории. Воспроизводимость отличается от сходимости тем, что оба результата должны быть получены в разных лабораториях.
Дата добавления: 2019-02-07 ; просмотров: 5106 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ