Что определяет среднюю скорость дрейфа свободных электронов
Микроскопический вид: скорость дрейфа
Физика > Микроскопический вид: скорость дрейфа
Рассмотрите скорость дрейфа электронов: роль проводников и электрического поля в движении зарядов, формула тока и дрейфа, скорость электрических сигналов.
Скорость дрейфа – средняя скорость, достигаемая частичкой из-за электрического поля.
Задача обучения
Основные пункты
Термин
Скорость дрейфа
Электрические сигналы перемещаются на больших скоростях. Достаточно хотя бы взглянуть на телефонные разговоры, транспортируемые токами в проводах и покрывающие огромные дистанции. Свет срабатывает, как только активируется переключатель.
Откуда такая высокая скорость у электрических сигналов? Дело в том, что сила между ними действует быстро на дистанции. Поэтому, когда свободный заряд вставляется в провод, входящий подталкивает к нему другие, которые и дальше нажимают на линии. В итоге, формируется электрическая ударная волна, проходящая сквозь систему практически со световой скоростью.
Когда заряженные частички вставляются в объем проводника, то равное число должно быстро удалиться. Отталкивание между подобными зарядами препятствует увеличению количества зарядов в объеме. Так что, по мере поступления одного заряда, второй убегает практически сразу, транспортируя сигнал вперед
Скорость дрейфа
Хорошие проводники обладает большим запасом свободных зарядов. В металлах – свободные электроны. Отдельный электрон между столкновением с атомами и прочими электронами перемещается на крошечную дистанцию, поэтому их пути оказываются практически случайными. Но проводники наделены электрическим полем, заставляющим электроны дрейфовать в конкретном направлении.
Скорость дрейфа электронов (vd) – средняя скорость свободных зарядов после воздействия поля. Она довольно небольшая, потому что присутствует много свободных зарядов. Если располагать плотностью свободных электронов в проводнике, то можно высчитать скорость дрейфа. Чем выше плотность, тем ниже скорость.
Свободные электроны часто сталкиваются. Здесь вы видите путь конкретной частички. Скорость дрейфа расположена в противоположном направлении электрическому полю для электронов. Коллизии обычно транспортируют энергию на проводник, нуждаясь в стабильном поступлении энергии для поддержания постоянного тока
Интересно, что x/Δt – величина скорости дрейфа vd, потому что заряды проходят среднюю дистанцию x за время t. Остальные показатели дают I = qnAvd.
Плотность тока – электрический ток на единицу площади поперечного сечения.
Что определяет среднюю скорость дрейфа свободных электронов
Подвижность. Дрейф носителей заряда
где qE = F – сила, действующая на электрон со стороны поля.
Подставив это выражение в формулу для скорости дрейфа, получаем
В формуле (3.1) величина 
называется подвижностью носителей заряда. Таким образом, подвижность носителей заряда обратно пропорциональна эффективной массе носителей m и прямо пропорциональна времени свободного пробега t п.
Иначе говоря, подвижность носителей заряда – это скорость дрейфа, приобретаемая свободными носителями в электрическом поле напряженности Е=1 В /м.
Оценка величины подвижности электрона μ в кристаллической решетке по формуле (3.1) дает следующее значение:
м 2 /В ·с.
Температурная зависимость величины подвижности носителей заряда в полупроводниках определяется механизмами рассеяния носителей заряда.
График зависимости m = f ( T) в сильно легированом полупроводнике представлен на рис. 3.1, б. Видно, что температурная зависимость подвижности носителей заряда в примесном полупроводнике состоит из двух участков. Участок 1 характерен для низких температур, когда преобладает рассеяние на ионизированных примесях; на участке 2 подвижность носителей уменьшается вследствие рассеяния на тепловых колебаниях атомов и ионов.
Результирующая подвижность m определяется с помощью соотношения
Подвижность и дрейфовая скорость носителей заряда зависят не только от температуры, но и от напряженности электрического поля в полупроводнике.
Величина подвижности носителей заряда, в свою очередь, зависит от напряженности электрического поля. При E >> vфон / m 0 подвижность уменьшается с ростом напряженности поля Е по закону m
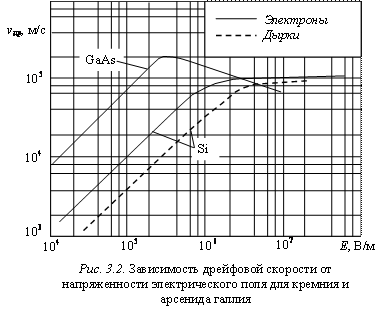
Для кремния и германия зависимость дрейфовой скорости от напряженности электрического поля может быть аппроксимирована формулой
Таким образом, дрейфовая скорость в полупроводниках возрастает с ростом напряженности электрического поля, достигая своего максимального значения – скорости насыщения, близкого к тепловой скорости.
Зависимость подвижности носителей заряда (электронов или дырок) от напряженности электрического поля в кремнии аппроксимируется выражением
Подвижность носителей заряда в средних и сильных электрических полях уменьшается с ростом напряженности электрического поля.
Создание в однородном полупроводнике электрического поля с напряженностью E, в результате подключения внешнего источника ЭДС или тока, приводит к появлению дрейфа носителей тока (электронов и дырок).
Поскольку знаки зарядов электронов и дырок противоположны, то носители дрейфуют со скоростью v др в противоположных направлениях в соответствии с силами, действующими со стороны электрического поля. Поэтому соответствующие дрейфовые токи складываются, как показано на рис. 3.3.
Плотность дрейфового тока jдр в собственном полупроводнике складывается из плотностей токов электронов j n др и дырок j p др и определяется из выражения
В примесных полупроводниках общая плотность дрейфового тока электронов и дырок
Что определяет среднюю скорость дрейфа свободных электронов
Подвижность. Дрейф носителей заряда
где qE = F – сила, действующая на электрон со стороны поля.
Подставив это выражение в формулу для скорости дрейфа, получаем
В формуле (3.1) величина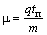 
называется подвижностью носителей заряда. Таким образом, подвижность носителей заряда обратно пропорциональна эффективной массе носителей m и прямо пропорциональна времени свободного пробега t п.
Иначе говоря, подвижность носителей заряда – это скорость дрейфа, приобретаемая свободными носителями в электрическом поле напряженности Е=1 В /м.
Оценка величины подвижности электрона μ в кристаллической решетке по формуле (3.1) дает следующее значение:
м 2 /В ·с.
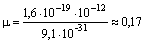
Температурная зависимость величины подвижности носителей заряда в полупроводниках определяется механизмами рассеяния носителей заряда.
График зависимости m = f ( T) в сильно легированом полупроводнике представлен на рис. 3.1, б. Видно, что температурная зависимость подвижности носителей заряда в примесном полупроводнике состоит из двух участков. Участок 1 характерен для низких температур, когда преобладает рассеяние на ионизированных примесях; на участке 2 подвижность носителей уменьшается вследствие рассеяния на тепловых колебаниях атомов и ионов.
Результирующая подвижность m определяется с помощью соотношения
Подвижность и дрейфовая скорость носителей заряда зависят не только от температуры, но и от напряженности электрического поля в полупроводнике.
Величина подвижности носителей заряда, в свою очередь, зависит от напряженности электрического поля. При E >> vфон / m 0 подвижность уменьшается с ростом напряженности поля Е по закону m
Для кремния и германия зависимость дрейфовой скорости от напряженности электрического поля может быть аппроксимирована формулой
Таким образом, дрейфовая скорость в полупроводниках возрастает с ростом напряженности электрического поля, достигая своего максимального значения – скорости насыщения, близкого к тепловой скорости.
Зависимость подвижности носителей заряда (электронов или дырок) от напряженности электрического поля в кремнии аппроксимируется выражением
Подвижность носителей заряда в средних и сильных электрических полях уменьшается с ростом напряженности электрического поля.
Создание в однородном полупроводнике электрического поля с напряженностью E, в результате подключения внешнего источника ЭДС или тока, приводит к появлению дрейфа носителей тока (электронов и дырок).
Поскольку знаки зарядов электронов и дырок противоположны, то носители дрейфуют со скоростью v др в противоположных направлениях в соответствии с силами, действующими со стороны электрического поля. Поэтому соответствующие дрейфовые токи складываются, как показано на рис. 3.3.
Плотность дрейфового тока jдр в собственном полупроводнике складывается из плотностей токов электронов j n др и дырок j p др и определяется из выражения
В примесных полупроводниках общая плотность дрейфового тока электронов и дырок
Когда к проводнику приложена разность потенциалов, свободные электроны между последовательными столкновениями приобретают скорость в направлении, противоположном электрическому полю (и теряют скорость при движении в направлении поля), таким образом приобретая компонент скорости в этом направлении в дополнение к его случайная тепловая скорость. В результате возникает определенная малая дрейфовая скорость электронов, которая накладывается на беспорядочное движение свободных электронов. Из-за этой скорости дрейфа возникает чистый поток электронов, противоположный направлению поля.
СОДЕРЖАНИЕ
Экспериментальная мера
Формула для оценки скорости дрейфа носителей заряда в материале постоянной площади поперечного сечения имеет вид:
Это также можно записать как:
Но плотность тока и скорость дрейфа j и u на самом деле являются векторами, поэтому это соотношение часто записывается как:
Числовой пример
ты знак равно А электрон м 3 ⋅ м 2 ⋅ C электрон знак равно C s 1 м ⋅ C знак равно м s <\ displaystyle u = <\ dfrac <\ text > <<\ dfrac <\ text >> < <\ dfrac <1><\ text >>> 
§ 100. Электрический ток. Сила тока (окончание)
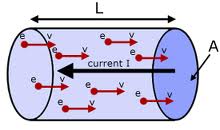
Связь силы тока со скоростью направленного движения частиц. Пусть цилиндрический проводник (рис. 15.2) имеет поперечное сечение площадью S. За положительное направление тока в проводнике примем направление слева направо. Заряд каждой частицы будем считать равным q0. В объёме проводника, ограниченном поперечными сечениями 1 и 2 с расстоянием Δl между ними, содержится nSΔl частиц, где n — концентрация частиц (носителей тока). Их общий заряд в выбранном объёме q = q0nSΔl. Если частицы движутся слева направо со средней скоростью υ, то за время 
все частицы, заключенные в рассматриваемом объёме, пройдут через поперечное сечение 2. Поэтому сила тока равна:
Важно
В СИ единицей силы тока является ампер (А).
Эта единица установлена на основе магнитного взаимодействия токов.
Измеряют силу тока амперметрами. Принцип устройства этих приборов основан на магнитном действии тока.
Определите среднюю квадратичную скорость теплового движения свободных электронов, рассматривая электронный газ как идеальный.
Скорость упорядоченного движения электронов в проводнике. Найдём скорость упорядоченного перемещения электронов в металлическом проводнике. Согласно формуле (15.2) 
где е — модуль заряда электрона.
Как видите, скорость упорядоченного перемещения электронов очень мала. Она во много раз меньше скорости теплового движения электронов в металле.
Условия, необходимые для существования электрического тока.
Важно
Для возникновения и существования постоянного электрического тока в веществе необходимо наличие свободных заряженных частиц.
Однако этого ещё недостаточно для возникновения тока.
Важно
Для создания и поддержания упорядоченного движения заряженных частиц необходима сила, действующая на них в определённом направлении.
Если эта сила перестанет действовать, то упорядоченное движение заряженных частиц прекратится из-за столкновений с ионами кристаллической решётки металлов или нейтральными молекулами электролитов и электроны будут двигаться беспорядочно.
На заряженные частицы, как мы знаем, действует электрическое поле с силой
= q
.
Важно
Обычно именно электрическое поле внутри проводника служит причиной, вызывающей и поддерживающей упорядоченное движение заряженных частиц. Только в статическом случае, когда заряды покоятся, электрическое поле внутри проводника равно нулю.
Если внутри проводника имеется электрическое поле, то между концами проводника в соответствии с формулой (14.21) существует разность потенциалов. Как показал эксперимент, когда разность потенциалов не меняется во времени, в проводнике устанавливается постоянный электрический ток. Вдоль проводника потенциал уменьшается от максимального значения на одном конце проводника до минимального на другом, так как положительный заряд под действием сил поля перемещается в сторону убывания потенциала.
Ключевые слова для поиска информации по теме параграфа.
Сила тока. Электронная теория проводимости
Вопросы к параграфу
1. Что определяет среднюю скорость дрейфа свободных электронов?
2. Почему единицу тока определяют по магнитному взаимодействию?
Образцы заданий ЕГЭ
1) 4 • 10 16 2) 8 • 10 17 3) 10 17 4) 2 • 10 17
А2. На электроды вакуумного диода подаётся переменное напряжение, в результате чего сила тока, проходящего через этот диод, равномерно увеличивается за 2 мкс от 0 до 12 А. Определите заряд, который прошёл через диод за это время.
А3. По проводнику идёт постоянный электрический ток. Значение заряда, прошедшего через проводник, возрастает с течением времени согласно графику, представленному на рисунке. Сила тока в проводнике равна