Что определяет спиновое квантовое число
СПИНОВОЕ КВАНТОВОЕ ЧИСЛО
Смотреть что такое «СПИНОВОЕ КВАНТОВОЕ ЧИСЛО» в других словарях:
спиновое квантовое число — sukinys statusas T sritis chemija apibrėžtis Mikrodalelės savasis judesio kiekio momentas, nesusijęs su jos judėjimu erdvėje. atitikmenys: angl. spin; spin quantum number rus. спин; спиновое квантовое число ryšiai: sinonimas – sukininis judesio… … Chemijos terminų aiškinamasis žodynas
спиновое квантовое число — sukinio kvantinis skaičius statusas T sritis chemija apibrėžtis Skaičius, apibūdinantis elementariųjų dalelių sukinį. atitikmenys: angl. spin quantum number rus. спиновое квантовое число … Chemijos terminų aiškinamasis žodynas
спиновое квантовое число — kvantinis sukinio skaičius statusas T sritis fizika atitikmenys: angl. spin quantum number vok. Spinquantenzahl, f rus. спиновое квантовое число, n pranc. nombre quantique de spin, m … Fizikos terminų žodynas
магнитное спиновое квантовое число — magnetinis kvantinis sukinio skaičius statusas T sritis fizika atitikmenys: angl. magnetic spin quantum number vok. magnetische Spinquantenzahl, f rus. магнитное спиновое квантовое число, n pranc. nombre quantique de spin magnétique, m … Fizikos terminų žodynas
МАГНЕТИЗМ МИКРОЧАСТИЦ — магн. свойства молекул, атомов, атомных ядер и субъядерных частиц (т. н. элементарных частиц). Магн. свойства элементарных частиц обусловлены наличием у них спина, а более сложных систем (ядер, атомов, молекул) особенностями их строения и вкладом … Физическая энциклопедия
СПЕКТРОСКОПИЯ — раздел физики, посвященный изучению спектров электромагнитного излучения. Здесь мы рассмотрим оптическую спектроскопию часто называют просто спектроскопией. Свет это электромагнитное излучение с длиной волны l от 10 3 до 10 8 м. Этот диапазон… … Энциклопедия Кольера
Список обозначений в физике — Необходимо проверить качество перевода и привести статью в соответствие со стилистическими правилами Википедии. Вы можете помочь … Википедия
Квантовая механика — волновая механика, теория устанавливающая способ описания и законы движения микрочастиц (элементарных частиц, атомов, молекул, атомных ядер) и их систем (например, кристаллов) а также связь величин, характеризующих частицы и системы, с… … Большая советская энциклопедия
МАГНИТНЫЙ МОМЕНТ — векторная величина, характеризующая магн. св ва в ва. М. м. обладают все элементарные частицы и образованные из них системы (атомные ядра, атомы, молекулы). М. м. атомов, молекул и др. многоэлектронных систем складывается из орбитальных М. м.… … Химическая энциклопедия
КВАНТОВАЯ МЕХАНИКА — изучает состояния микрочастиц и их систем (элементарных частиц, атомных ядер, атомов, молекул, кристаллов), изменение этих состояний во времени, а также связь величин, характеризующих состояния микрочастиц, с эксперим. макроскопич. величинами. К … Химическая энциклопедия
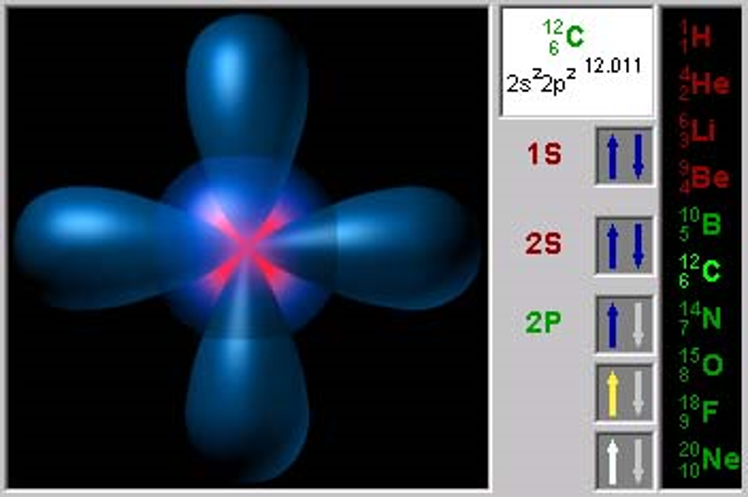
Квантовые числа электронов.
Квантовые числа – энергетические параметры, определяющие состояние электрона и тип атомной орбитали, на которой он находится.
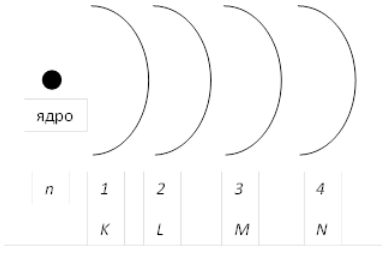
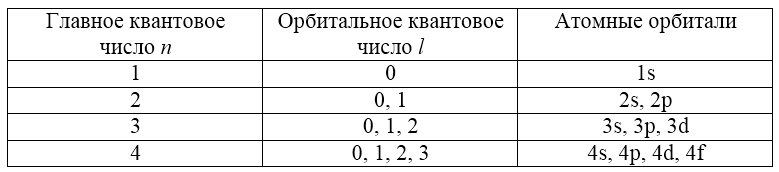
1. Главное квантовое число n характеризует общую энергию электрона и размер орбитали. Оно принимает целочисленные значения от 1: n = 1, 2, 3, 4, 5, 6, 7.
2. Орбитальное (побочное) квантовое число l характеризует форму атомной орбитали и принимает значения от 0 до n-1: 0, 1, 2, 3, …, n-1.
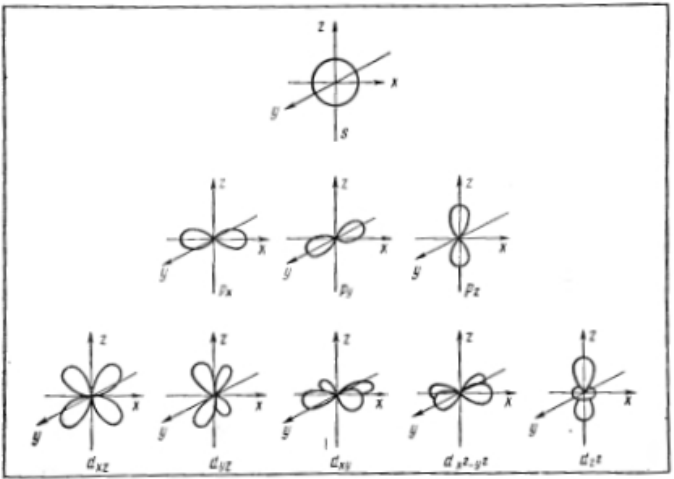
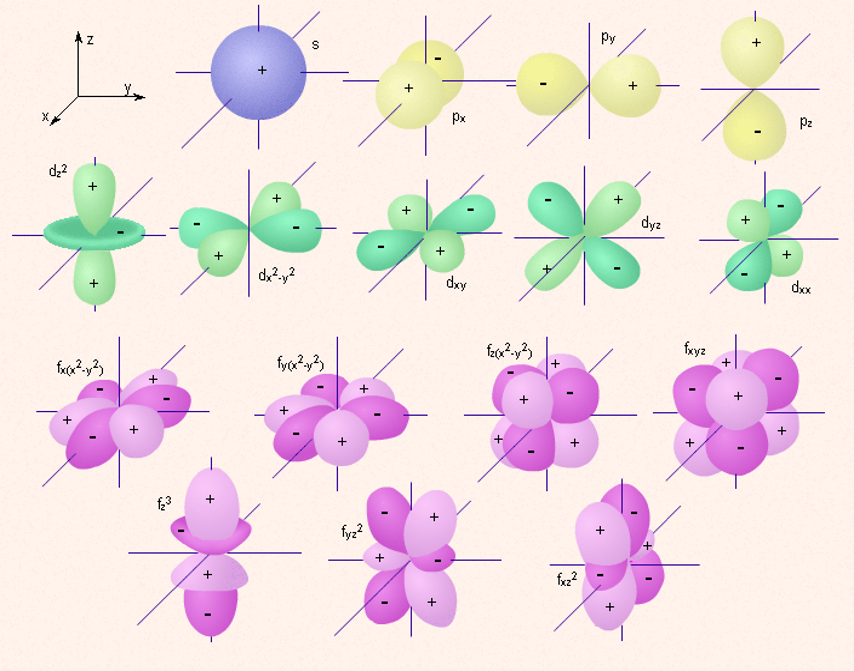
Электрон, обладая свойствами частицы и волны, движется вокруг ядра, образуя электронное облако, форма которого в s-, р-, d-, f-, g-состояниях различна.
Если l=0 (s-орбиталь), то электронное облако имеет сферическую форму и не обладает направленностью в пространстве.
Если l=1 (p-орбиталь) то электронное облако имеет форму гантели.
d- и f-орбитали имеют более сложную форму.
3. Магнитное квантовое число m характеризует количество орбиталей одинаковой формы и их ориентацию относительно внешнего электрического или магнитного поля. Квантовое число m принимает целочисленные значения в интервале –l, … –1, 0, +1, … +l. Для каждого значения разрешено 2l+1 значений числа m. Например, если l=1, то m имеет 2×1+1, т.е. 3 значения: –1, 0, +1.
4. Спиновое квантовое число s характеризует вращение электрона вокруг своей оси и принимает только 2 значения: +1/2 (↑) и –1/2 (↓).
Квантование
Вы будете перенаправлены на Автор24
Введение
Состояние каждого электрона в атоме описывается волновой функцией, которая называется атомной орбиталью (или уровнем) и характеризуется тремя квантовыми числами. Соответствующие волновые функции выводятся из уравнения Шредингера и должны удовлетворять следующим требованиям: непрерывность, однозначность и конечность каждой волновой функции. При нарушении хотя бы одного из этих требований волновая функция оказывается непригодной для описания состояния электронов в атоме. Следовательно, дискретность энергетических состояний, в которых могут находиться электроны в атоме, является прямым следствием уравнения Шредингера. То же касается и трех квантовых чисел.
Главное квантовое число
Главное квантовое число может принимать любое целочисленное значение:
Рисунок 1. Схема раположений орбиталей атома
Орбитальное квантовое число
Готовые работы на аналогичную тему
Магнитное квантовое число
Спиновое квантовое число
Примеры решения типовых задач
Записать электронную конфигурацию атома гелия в основном состоянии.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 16 03 2021
Строение атома, главное квантовое число. Побочное (орбитальное) квантовое число. Магнитное квантовое число. Спиновое квантовое число
Страницы работы
Фрагмент текста работы
определяет пространственное расположение атомной орбитали и принимает целые значения от –l до + l через нуль, то есть 2l + 1 значений.
Изображение с помощью граничных поверхностей s-, p-, d- и f-орбиталей.
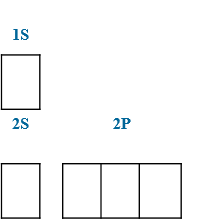
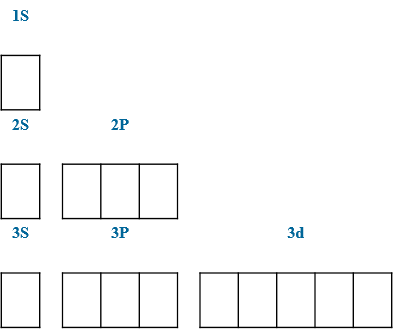
Заполнение атомных орбиталей
Принцип наименьшей энергии
Последовательность застройки электронной оболочки многоэлектронного атома подчиняется следующим эмпирическим правилам:
Электронные формулы 8О 1s22s22p4 16S 1s22s22p63s23p4
В=4 *S 1s22s22p63s23p33d1
В=6 *S 1s22s22p63s13p33d2
Спин электрона. Спиновое квантовое число
О. Штерн и В. Герлах, проводя прямые измерения магнитных моментов (см. § 131), обнаружили в 1922 г., что узкий пучок атомов водорода, заведомо находящихся в ^-состоянии, в неоднородном магнитном поле расщепляется на два пучка. В этом состоянии момент импульса электрона равен нулю (см. (223.4)). Магнитный момент атома, связанный с орбитальным движением электрона, пропорционален механическому моменту (см. (131.3)), поэтому он равен нулю и магнитное поле не должно оказывать влияния на движение атомов водорода в основном состоянии, т. е. расщепления быть не должно. Однако в дальнейшем при применении спектральных приборов с большой разрешающей способностью было доказано, что спектральные линии атома водорода обнаруживают тонкую структуру (являются дублетами) даже в отсутствие магнитного поля.
Для объяснения тонкой структуры спектральных линий, а также ряда других трудностей в атомной физике американские физики Д. Уленбек (1900—1974) и С. Гаудсмит (1902—1979) предположили, что электрон обладает собственным неуничтожимым механизмом моментом импульса, не связанным с движением электрона в пространстве, — спином (см. § 131).
Спин электрона (и всех других микрочастиц) — квантовая величина, у нее нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.
Если электрону приписывается собственный механический момент импульса (спин) Ls, то ему соответствует собственный магнитный момент pms. Согласно общим выводам квантовой механики, спин квантуется по закону
где s — спиновое квантовое число.
По аналогии с орбитальным моментом импульса, проекция Laспина квантуется так, что вектор L, может принимать 2s + 1ориентации. Так как в опытах Штерна и Герлаха наблюдались только две ориентации, то 2s+1=2,откуда s = ½. Проекция спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется выражением, аналогичным (223.6):
где ms— магнитное спиновое квантовое число; оно может иметь только два значения:
Таким образом, опытные данные привели к необходимости характеризовать электроны (и микрочастицы вообще) добавочной внутренней степенью свободы. Поэтому для полного описания состояния электрона в атоме необходимо наряду с главным, орбитальным и магнитным квантовыми числами задавать еще магнитное спиновое квантовое число.
Принцип неразличимости тождественных
Частиц. Фермионы и бозоны
Если перейти от рассмотрения движения одной микрочастицы (одного электрона) к многоэлектронным системам, то проявляются особые свойства, не имеющие аналога в классической физике. Пусть квантово-механическая система состоит из одинаковых частиц, например электронов. Все электроны имеют одинаковые физические свойства — массу, электрический заряд, спин и другие внутренние характеристики (например, квантовые числа). Такие частицы называют тождественными.
Необычные свойства системы одинаковых тождественных частиц проявляются в фундаментальном принципе квантовой механики — принципе неразличимости тождественных частиц, согласно которому невозможно экспериментально различить тождественные частицы.
В классической механике даже одинаковые частицы можно различить по положению в пространстве и импульсам. Если частицы в какой-то момент времени пронумеровать, то в следующие моменты времени можно проследить за траекторией любой из них. Классические частицы, таким образом, обладают индивидуальностью, поэтому классическая механика систем из одинаковых частиц принципиально не отличается от классической механики систем из различных частиц.
В квантовой механике положение иное. Из соотношения неопределенностей вытекает, что для микрочастиц вообще неприменимо понятие траектории; состояние микрочастицы описывается волновой функцией, позволяющей вычислять лишь вероятность (|Y| 2 ) нахождения микрочастицы в окрестностях той или иной точки пространства. Если же волновые функции двух тождественных частиц в пространстве перекрываются, то разговор о том, какая частица находится в данной области, вообще лишен смысла: можно лишь говорить о вероятности нахождения в данной области одной из тождественных частиц. Таким образом, в квантовой механике тождественные частицы полностью теряют свою индивидуальность и становятся неразличимыми. Следует подчеркнуть, что принцип неразличимости тождественных частиц не является просто следствием вероятностной интерпретации волновой функции, а вводится в квантовую механику как новый принцип, который, как уже указывалось, является фундаментальным.
Принимая во внимание физический смысл величины | Y | 2 , принцип неразличимости тождественных частиц можно записать в виде

где х1 и х2— соответственно совокупность пространственных и спиновых координат первой и второй частиц. Из выражения (226.1) вытекает, что возможны два случая:
т. е. принцип неразличимости тождественных частиц ведет к определенному свойству симметрии волновой функции. Если при перемене частиц местами волновая функция не меняет знака, то она называется симметричной, если меняет — антисимметричной. Изменение знака волновой функции не означает изменения состояния, так как физический смысл имеет лишь квадрат модуля волновой функции. В квантовой механике доказывается, что характер симметрии волновой функции не меняется со временем. Это же является доказательством того, что свойство симметрии или антисимметрии — признак данного типа микрочастиц.
Установлено, что симметрия или антисимметрия волновых функций определяется спином частиц. В зависимости от характера симметрии все элементарные частицы и построенные из них системы (атомы, молекулы) делятся на два класса. Частицы с полуцелым спином (например, электроны, протоны, нейтроны) описываются антисимметричными волновыми функциями и подчиняются статистике Ферми — Дирака; эти частицы называются фермионамн. Частицы с нулевым или целочисленным спином (например, p-мезоны, фотоны) описываются симметричными волновыми функциями и подчиняются статистике Бозе — Эйнштейна; эти частицы называются бозонами. Сложные частицы (например, атомные ядра), составленные из нечетного числа фермионов, являются фермионами (суммарный спин — полуцелый), а из четного — бозонами (суммарный спин целый).
Зависимость характера симметрии волновых функций системы тождественных частиц от спина частиц теоретически обоснована швейцарским физиком В. Паули (1900—1958), что явилось еще одним доказательством того, что спин является фундаментальной характеристикой микрочастиц.