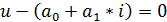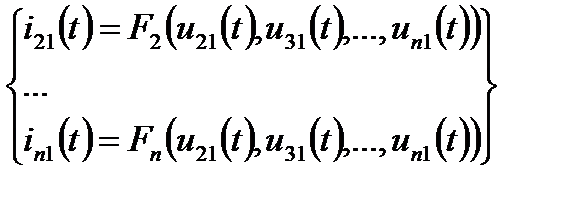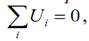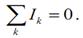Что описывают компонентные уравнения

Компонентные и системные уравнения, описывающие цепь

Закономерности, описывающие поведение элементов цепи (элементные или компонентные законы)

Это математические выражения, связывающие между собой переменные, описывающие состояние элемента – токи через выводы элемента и напряжения между выводами этого элемента. Такие математические уравнения называют элементными или компонентными законами. Такие законы могут иметь вид алгебраических или дифференциальных уравнений. Количество таких уравнений для элемента с n выводами равно (n‑1).

Простейший вид элемента – с двумя выводами (двухполюсник). Его поведение описывается зависимостью между двумя величинами: iиu. Ее называют вольт-амперной характеристикой ВАХ.

Какая из переменных является независимой (аргументом) – любая.
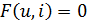
С математической точки зрения – любая.

Как можно определить ВАХ экспериментально? Изменяя одну из величин и измеряя обе.

Элемент называют линейным, если ВАХ – полином первого порядка

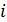
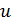
Может ли быть так, что при заданном значении аргумента функция не определяется однозначно?
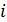
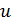
Может ли быть так, что при постоянном значении аргумента функция не сохраняет постоянства?

Пример с конденсатором.
Пример с термозависимым резистором (саморазогрев).
Пример с диодом – нелинейный элемент

Эксперимент по снятию ВАХ резистора и полупроводникового диода а) вручную, б) с помощью характериографа

Простой вариант формирования системы компонентных уравнений для n-полюсника:

· Выбрать один из выводов в качестве базового.

· Задать величины напряжений между каждым из оставшихся и базовым выводом (возможность этого является следствием второго закона Кирхгофа).

· Измерять токи через каждый из выводов за исключением базового.

Система из (n-1) уравнений, описывающая поведение n-полюсника будет иметь вид

здесь F символизирует зависимость, которая может быть алгебраической, либо содержать производные и (или) интегралы переменных u(t) и i(t).

Энергетические свойства элементов электрических цепей.

Диссипативность: (необратимое) превращение электрической энергии в тепло

Переход части электрической энергии в тепло при протекании тока по диссипативным элементам. Компонентное уравнение диссипативного элемента цепи. Потери энергии в электронных информационных устройствах. Почему энергия не может быть сколь-угодно малой.

Большая группа элементов цепей обладает свойством, состоящим в том, что вся энергия, доставляемая токами, протекающими через выводы, превращается внутри таких элементов в тепло. Такие элементы называют диссипативными[2]. Примером такого элемента является резистор, используемый в электронных цепях для …. () Компонентное уравнение диссипативного двухполюсника имеет вид

(2.4)

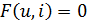
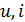
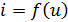
Запись уравнения в таком виде подчёркивает тот факт, что ни одна из двух переменных не является причиной изменения другой величины, т.е. аргументом, независимой переменной, может быть любая из них. Во многих книгах утверждается (считается), что независимой переменной, причиной является изменение напряжения, в то время как изменение тока это следствие, и компонентное уравнение переписывают в виде

(2.5)

Однако утверждение о «первичности» напряжения ошибочно.

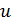
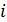
Характеристики диссипативных элементов часто называют «вольт-амперными», поскольку в выражении присутствуют две переменные: напряжение и ток . И вновь отметим, что в приведённом уравнении обе переменные могут изменяться во времени.

Вольт-амперная характеристика 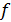может быть функцией любого вида. Так, например, у полупроводниковых диодов характеристики существенно нелинейны и весьма различны для разных типов диодов.

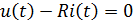
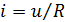
Для металлических проводников компонентная зависимость весьма близка к прямой пропорциональной ‑ это всем известный «закон Ома» , записываемый обычно в виде . Однако при значительной величине тока вследствие саморазогрева зависимость может оказаться весьма «причудливой» (например, для нити лампы накаливания).

В электротехнических устройствах используются многочисленные элементы с числом выводов, превышающим два. Прежде всего, это транзисторы, у которых три вывода (у некоторых полевых транзисторов может быть четыре вывода). Вольт-амперные характеристики многополюсных диссипативных элементов представляют собой семейство функций нескольких аргументов. Количество функций, а также количество аргументов в каждой функции на единицу меньше количества выводов многополюсника.

Емкость: (обратимое) накопление энергии в электрическом поле (заряженного конденсатора).

Запасание части электрической энергии в реактивных элементах цепи ‑ в виде энергии электрического поля в конденсаторе или в виде энергии магнитного поля в индукторе. Компонентные уравнения реактивных элементов (накопителей энергии).

Некоторые виды элементов цепей способны обратимо накапливать электрическую энергию в электрическом или в магнитном поле.

Компонентное уравнение элемента цепи, способного накапливать энергию в электрическом поле (электростатического накопителя), в общем случае имеет вид

(2.6)

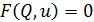
Это соотношение иногда называют «вольт-кулонной» характеристикой. Однако при описании электрической цепи, содержащей электростатический накопитель, состояние цепи описывают, используя только напряжения и токи (и, может быть, их производные и интегралы). Этого можно достигнуть, использовав соотношение между зарядом и током (используемого в определении единицы заряда ):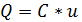

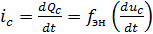
(2.7)

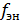
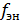
Любой фрагмент электрической цепи, в котором имеются две точки, между которыми существует ненулевое напряжение, обладает свойствами электростатического накопителя. Вид функции зависит от свойств среды, окружающей фрагмент цепи. (Правильные, но непонятные слова). Известно более 300 веществ (сегнетоэлектрики), для которых функция существенно нелинейна.

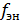
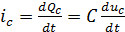
Для большинства веществ функция имеет вид прямой пропорциональной зависимости:

(2.8)

В последней формуле 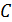– электрическая ёмкость электростатического накопителя, постоянный параметр, измеряемый в фарадах.

Изготавливаются и используются в электрических цепях конденсаторы – двухполюсники, обладающие свойством электростатического накопителя. При проектировании и изготовлении конденсаторов принимают специальные меры для обеспечения постоянства величины их емкости.

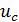
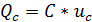
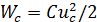
Конденсатор, заряженный до напряжения (и хранящий заряд ) в своём электрическом поле, в соответствии с (2.1) содержит энергию . Из формулы вольт-кулонной характеристики (2.6) и (2.7) могут быть сделаны весьма важные для дальнейшего выводы:
а) скорость изменения напряжения на электростатическом накопителе тем больше, чем больше величина перезаряжающего тока,
б) напряжение на электростатическом накопителе не может измениться скачком, поскольку для этого необходим ток бесконечно большой величины, что физически не реализуемо.

Индуктивность: (обратимое) накопление энергии в магнитном поле тока.

Компонентное уравнение элемента цепи, способного накапливать энергию в магнитном поле (электромагнитного накопителя), имеет вид:

(2.9)

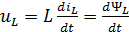
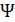
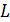
Соотношение (2.9) иногда называют «вебер-амперной характеристикой», поскольку оно устанавливает связь между величиной суммарного магнитного потока (потокосцепления) и величиной тока, создающего этот поток. Величина потокосцепления измеряется в веберах, (как и магнитный поток). Коэффициент пропорциональности называется индуктивностью и измеряется в единицах генри.

Любой фрагмент реальной электрической цепи в некоторой степени обладает свойствами магнитного накопителя, поскольку вокруг проводника с током всегда возникает магнитное поле.

Из формулы вебер-амперной характеристики (2.9) следуют важные для дальнейшего изложения выводы
а) скорость изменения тока в электромагнитном накопителе тем больше, чем больше величина напряжения между его выводами,
б) ток в магнитном накопителе не может измениться скачком, поскольку для этого напряжение между выводами магнитного накопителя должно стать бесконечно большим, что физически не реализуемо.

Для линейных двухполюсников математическое выражение этих свойств:

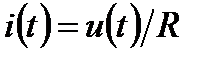
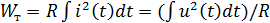
Резистивность (диссипативность): и
это соотношение известно как Закон Ома – ВАХ идеального резистора

Емкость электрическая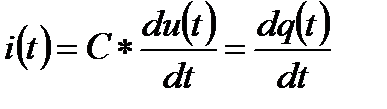
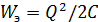
вольт-кулонная характеристика электростатического накопителя энергии

Индуктивность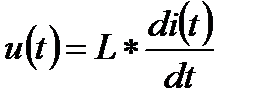
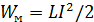
вебер-амперная характеристика электромагнитного накопителя энергии

Два последних соотношения никак не называются, хотя все три формулы представляют собой простейшие математические модели для трех видов двухполюсников: резистора, конденсатора и катушки индуктивности (индуктора).

Любой реальный двухполюсник обладает всеми тремя свойствами, только в разной степени.

В каких случаях можно пренебречь отдельными свойствами. На этот вопрос можно ответить, проведя анализ энергетического баланса.

Источник

Компонентные и топологические уравнения электрической цепи

Математическое описание процессов в сложных цепях, состоящих из большого числа элементов, основывается на компонентных и топологических уравнениях.

Компонентныминазываются уравнения, которые устанавливают зависимость между разнотипными переменными, относящиеся к одному из элементов цепи, например, уравнения (2.1), (2.5) и (2.10), связывающие ток и напряжение в пассивных элементах цепи , , .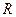

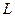
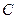
Используя компонентные уравнения, можно составить уравнение, связывающие напряжение и ток любой ветви электрической цепи. Например, для ветви, показанной на рис. 3.5, такое уравнение будет иметь вид

.

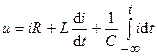
Топологическиминазываются уравнения, которые устанавливают зависимость между однотипными переменными цепи, обусловленную структурой цепи, например, уравнения, которые устанавливают зависимость между токами либо между напряжениями ветвей цепи. Примером таких уравнений являются уравнения, которые составляются на основании законов Кирхгофа, сформулированные Густавом Кирхгофом в 1845 году.

Согласно первому закону Кирхгофаалгебраическая сумма токов ветвей, подключенных к одному и тому же узлу цепи, равна нулю

, (3.1)

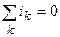
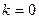
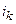
где — номер ветви, подключенной к рассматриваемому узлу; — ток k-ой ветви.

При составлении уравнения (3.1) токи, направленные к узлу, записываются в уравнение со знаком «плюс», а токи, направленные от узла, — со знаком «минус». С физической точки зрения первый закон Кирхгофа выражает тот факт, что в узле электрической цепи невозможно ни накопления, ни исчезновение электрического заряда, то есть сколько электрических зарядов подходит к узлу, столько же и уходит от него за один и тот же промежуток времени.

Число независимых уравнений, которые можно составить по первому закону Кирхгофа, определяется числом независимых узлов цепи

,

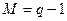
где 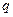— общее число узлов цепи.

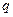
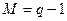
Последний -й узел является зависимым, поскольку уравнение, составленное для него по первому закону Кирхгофа, может быть получено путём линейного преобразования уравнений, составленных для остальных узлов цепи.

Например, для узла цепи, показанной на рис. 3.6, уравнение, составленное по первому закону Кирхгофа, будет иметь вид

.

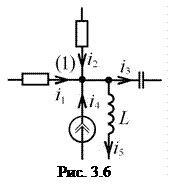
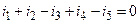
Если в последнем уравнении токи, втекающие в узел, оставить в левой части уравнения, а токи, вытекающие из узла, перенести в правую части уравнения, то получим уравнение

,

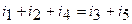
в соответствии с которым первый закон Кирхгофа можно сформулировать следующим образом: в любой момент времени сумма токов, втекающих в узел, равна сумме токов, вытекающих из этого узел.

Второй закон Кирхгофагласит, что алгебраическая сумма напряжений на пассивных элементах и источниках тока, входящих в состав замкнутого контура электрической цепи, равна алгебраической сумме э.д.с. идеальных источников напряжения, действующих в этом контуре,

, (3.2)

где — номер ветви; — алгебраическая сумма напряжений на пассивных элементах и источнике тока, водящего в состав -ой ветви; — э.д.с. -го идеального источника напряжения, действующего в контуре.

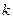
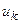
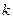
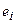
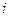
Если направление напряжения на элементе ветви контура совпадает с направлением обхода контура, то оно записываются в левую часть уравнения (3.2) со знаком «плюс», в противном случае оно записывается со знаком «минус». Аналогичным образом записываются в правую часть уравнения (3.2) э.д.с. идеальных источников напряжения, действующих в контуре.

С физической точки зрения второй закон Кирхгофа выражает тот факт, что работа по перемещению единичного электрического заряда по замкнутому контуру цепи равна нулю.

Число независимых уравнений, которые можно составить по второму закону Кирхгофа равно число независимых контуров цепи, которое, в свою очередь, определяется числом главных ветвей графа цепи,

,

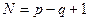
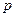
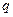
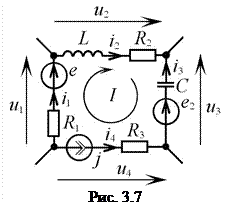
где и — общее число ветвей и узлов электрической цепи соответственно.

Например, для контура электрической цепи (рис. 3.7) уравнение, составленное по второму закону Кирхгофа, будет иметь вид

,

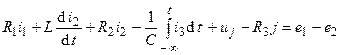
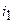
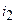
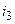
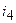
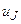
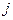
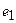
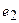
где , , , — токи ветвей; — напряжение на источнике тока , действующем в 4-ой ветви; и — э.д.с. источников напряжения, действующих в контуре.

Перегруппировав слагаемые в (3.2), можно записать второй закон Кирхгофа в виде

, (3.3)

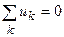
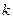
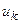
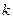
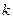
где — номер ветви контура; — напряжение -ой ветви, которое. определяется как алгебраическая сумма напряжений на пассивных элементах, а также на источниках тока и э.д.с., входящих в состав -ой ветви

В соответствии с уравнением (3.3) второй закон Кирхгофа можно сформулировать следующим образом. Алгебраическая сумма напряжений ветвей, образующих замкнутый контур электрической цепи, равна нулю.

Напряжения ветвей, направления которых совпадают с направлением обхода контура, подставляют в уравнение (3.3) со знаком «плюс», а не совпадающие — со знаком «минус». Уравнения (3.2) и (3.3) идентичны. Для расчётов уравнение (3.2) является более удобным, поскольку в нём неизвестные напряжения на пассивных элементах и источниках тока записаны в левой части уравнения, а известные э.д.с. источников напряжения — в правой части уравнения, что уменьшает вероятность ошибок при составлении уравнений.

Дата добавления: 2017-09-01 ; просмотров: 5324 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

44. Поэлементное описание: способы получения компонентных и топологических уравнений.

Основные физические свойства технических объектов любой физической природы – инерционные, упругие и диссипативные. Они отображаются в динамических моделях соответственно инерционными, упругими и диссипативными элементами.

При моделировании методом функционально законченных элементов элементы обычно обладают несколькими физическими свойствами и являются сложными. При имитационном моделировании все элементы простые, так как каждый из них наделён только одним физическим свойством. Мы в данном описании рассматриваем только простые элементы. Состояние простого элемента характеризуется одной потоковой переменной и одной потенциальной переменной. Зависимость между этими переменными называют компонентным уравнением.

Компонентные уравнения элементов могут быть получены путем непосредственного использования физических законов и имеют следующий вид:

1) для инерционного элемента

(5.1)

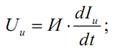
2) для диссипативного элемента

(5.2)

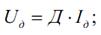
3) для упругого элемента

(5.3)

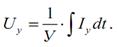
В уравнениях (5.1)-(5.3) приняты следующие обозначения: И, Д, У – параметры инерционного, диссипативного и упругого элементов соответственно; I – потоковая переменная; U – потенциальная переменная. Индексы при переменных I и U указывают на принадлежность их соответствующим элементам.

Для получения полной математической модели технической системы необходимо объединить все компонентные уравнения элементов в общую систему уравнений. Объединение осуществляется на основе физических законов, выражающих условия равновесия и непрерывности физических переменных. Уравнения этих законов называют топологическими уравнениями. Они описывают характер взаимодействия между простыми элементами, устанавливая соотношения между однотипными переменными. Условия равновесия записываются для потенциальных переменных:

а условия непрерывности – для потоковых переменных:

Форма компонентных и топологических уравнений одинакова для систем различной физической природы. Топологическое уравнение для векторных переменных формулируется как равенство нулю геометрической суммы

соответствующих координат, а для скалярных – равенство нулю алгебраической суммы этих координат.

Полная математическая модель технического объекта, составленная на основе компонентных уравнений, представляет собой систему обыкновенных дифференциальных уравнений.

Искомыми функциями в этих уравнениях являются базисные переменные (координаты) I и U, а независимой переменной – время t. Размерность математической модели определяется общим порядком системы дифференциальных уравнений (или числом базисных переменных). Эту модель обычно представляют в нормальной форме Коши, в которой все уравнения разрешены относительно первых производных координат dI/dt и dU/dt. Координатный базис в этом случае составляют потоковые переменные I и потенциальные переменные U.

Поведения большинства физических систем можно охарактеризовать с помощью фазовых переменных. Фазовая переменная (ФП) – это величина, характеризующая физическое или информационное состояние моделируемого объекта. Так, в электрической системе ФП это токи и напряжения, в механической системе – силы и скорости.

Законы функционирования элементов системы задаются компонентными уравнениями. Они описывают связь ФП разного типа для каждого элемента технической системы. Компонентные уравнения – это уравнения математических моделей элементов системы. Они могут быть линейными, нелинейными, алгебраическими, дифференциальными или интегральными. Каждый элемент моделируемого объекта должен иметь компонентное уравнение. Для большинства элементов такие уравнения уже получены, их используют при моделировании. Например, в гидравлике для дросселя есть аналитическое выражение, которое связывает расход и давления. Связь между однородными ФП, которые относятся к разным элементам в подсистемах, устанавливается топологическими уравнениями. Они отображают топологию взаимосвязей элементов. Их получают на основе данных о структуре системы. Примеры топологических уравнений: в электрических системах – уравнения на основе законов Кирхгофа; в механических системах – уравнения, отражающие принципы Д’Аламбер и добавление скоростей и т.д. Очевидно, что процедура разработки топологических уравнений выполняется для каждого моделирующего объекта, поскольку структуры объектов различны.

Математическую модель системы получают объединением компонентных и топологических уравнений этой системы.

Источник