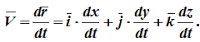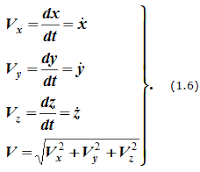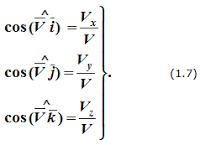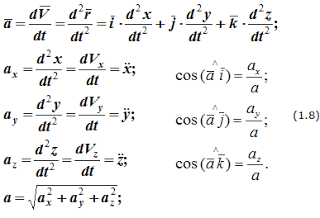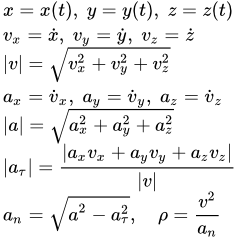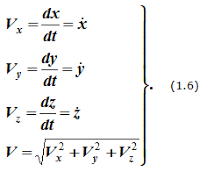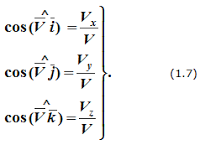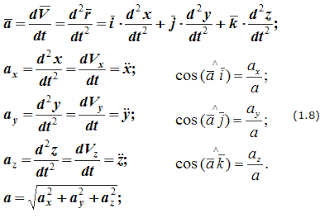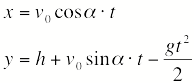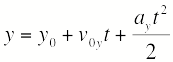Что необходимо знать при координатном способе задания движения точки
iSopromat.ru
При координатном способе задания движения точки в выбранной системе координат задаются координаты движущейся точки как функции от времени.
В прямоугольной декартовой системе координат это будут уравнения:
Эти уравнения являются и уравнениями траектории в параметрической форме. Исключая из этих уравнений параметр t, можно получить три пары систем двух уравнений, каждая из которых представляет траекторию точки, как пересечение поверхностей.
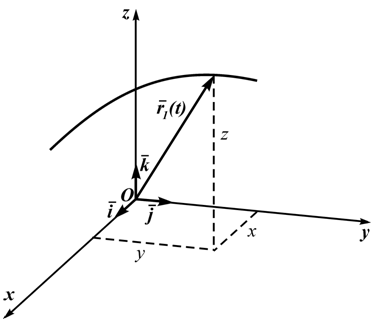
Кроме декартовых могут быть использованы другие системы координат (сферическая, цилиндрическая). Всегда можно перейти от координатного способа задания движения к векторному (рисунок 1.3):
Поэтому, используя формулы для определения скорости и ускорения точки при векторном способе задания движения, можно получить аналогичные формулы для координатного способа:
Направление вектора скорости определяется с помощью направляющих косинусов:
Формулы (1.6) и (1.7) полностью определяют вектор скорости при координатном способе задания движения точки, т.е. по величине и направлению.
Аналогичны формулы для определения ускорения точки:
Формулы (1.8) определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных учебниках обозначения проекций скоростей и ускорений точек на оси декартовой системы координат.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
iSopromat.ru
Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.
Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.
В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.
Векторный
При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.
Координатный
При координатном способе задания движения задаются координаты точки как функции времени:
Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.
Естественный
При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Координатный способ задания движения точки
Введение
Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы применим основные результаты этой теории к координатному способу задания движения материальной точки.
Далее мы приводим формулы вычисления кинематических величин и пример решения задачи для координатного способа задания движения.
Определение кинематических величин
Радиус кривизны траектории:
.
Центр кривизны траектории:
.
Единичный вектор в направлении бинормали:
.
Пример решения задачи
Определение скорости и ускорения точки по заданным уравнениям ее движения
По заданным уравнениям движения точки установить вид ее траектории и для момента времени найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Уравнения движения точки:
, см;
, см.
Решение
Определение вида траектории
Поскольку
, то
; или
.
Аналогичным образом получаем ограничение для координаты :
;
;
Строим параболу по точкам.
| 0 | 6 |
| ± 3 | 5,625 |
| ± 6 | 4,5 |
| ± 9 | 2,625 |
| ± 12 | 0 |
Определение скорости точки
Вычисляем значения компонент скорости в момент времени :
;
.
Модуль скорости:
.
Определение ускорения точки
Вычисляем значения компонент ускорения в момент времени :
;
.
Модуль ускорения:
.
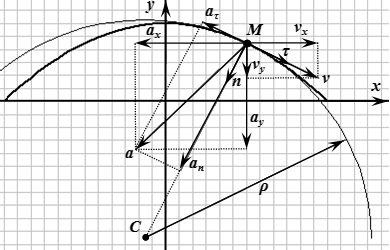
Нормальное ускорение:
.
Вектор и направлен в сторону центра кривизны траектории.
Радиус кривизны траектории:
.
Определение остальных величин
Определим остальные величины.
Единичный вектор в направлении касательной к траектории:
.
Вектор тангенциального ускорения:
.
Вектор нормального ускорения:
.
Единичный вектор в направлении главной нормали:
.
Координаты центра кривизны траектории:
.
Теоретическая механика
16. Кинематика точки. Способы задания движения точки (векторный и координатный)
Кинематика изучает простейшую форму движения – механическое движение. Кинематически определить движение тела – это значит указать его положение относительно выбранной системы отсчета в каждый момент времени.
Движение материальной точки (в дальнейшем будем говорить просто точки) задано, если известен закон движения.
Закон движения. Закон движения – это уравнение, позволяющее определить положение точки относительно выбранной системы отсчета в любой момент времени.
Основная задача кинематики точки. По известному закону движения определить траекторию движения точки, ее положение на траектории, скорость и ускорение точки в ее положении на траектории.
Способы задания движения точки
В зависимости от выбора системы отсчета существуют три способа задания движения точки – векторный, координатный и естественный. Рассмотрим эти способы задания движения в отдельности.
Векторный способ задания движения точки
Таким образом, вектор 
определяет положение движущейся точки в любой момент времени. Следовательно, уравнение является законом движения при векторном способе задания движения.
Величина 
называется вектором скорости точки. Вектор скорости точки всегда направлен по касательной к годографу (траектории движения точки) в сторону перемещения точки.
Величина 
называется вектором ускорения точки.
Как показано на рис.К.10, вектор 
направлен в сторону вогнутости траектории движения точки, следовательно и вектор ускорения 
всегда направлен в ту же сторону, то есть в сторону вогнутости траектории движения точки.
Координатный способ задания движения точки
Компоненты скорости и ускорения движущейся точки в любой момент времени определяются по формулам
Модули скорости и ускорения 
Координатный способ задания движения точки
В выбранной системе координат задаются координаты движущейся точки как функции от времени. В прямоугольной декартовой системе координат это будут уравнения:
x=x(t)
y=y(t)
Эти уравнения являются и уравнениями траектории в параметрической форме. Исключая из этих уравнений параметр t, можно получить три пары систем двух уравнений, каждая из которых представляет траекторию точки, как пересечение поверхностей.
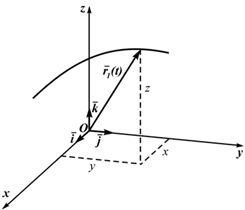
Кроме декартовых могут быть использованы другие системы координат (сферическая, цилиндрическая). Всегда можно перейти от координатного способа задания движения к векторному (рисунок 1.3):
r(t)=i⋅x(t) ⊕ j⋅y(t) ⊕ k⋅z(t) (1.5)
Поэтому, используя формулы для определения скорости и ускорения точки при векторном способе задания движения, можно получить аналогичные формулы для координатного способа:
Направление вектора скорости определяется с помощью направляющих косинусов:
Формулы (1.6) и (1.7) полностью определяют вектор скорости при координатном способе задания движения точки, т.е. по величине и направлению.
Аналогичны формулы для определения ускорения точки:
Формулы (1.8) определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных учебниках обозначения проекций скоростей и ускорений точек на оси декартовой системы координат.
3 Баллистическое движение.Криволинейное баллистическое движение тела можно рассматривать как результат сложения двух прямолинейных движений: равномерного движения по оси х и равнопеременного движения по оси у.
| Закон баллистического движения в координатной форме |
На рисунках показаны траектории движения, векторы начальной и мгновенной скоростей тела, брошенного под углом к горизонту, и тела, начальная скорость которого направлена горизонтально.