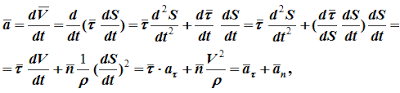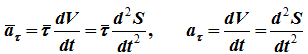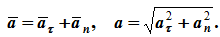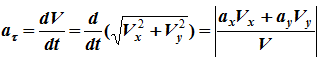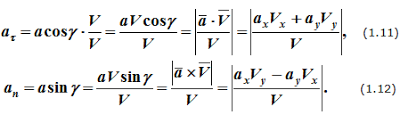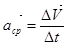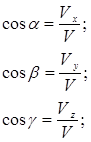Что необходимо знать при естественном способе задания движения точки

iSopromat.ru

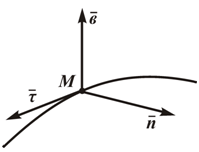
При естественном способе задания движения точки предполагается определение параметров движения точки в подвижной системе отсчета, начало которой совпадает с движущейся точкой, а осями служат касательная, нормаль и бинормаль к траектории движения точки в каждом ее положении.

Единичные орты τ, n, b определяют направление соответствующих осей в каждой точке кривой.

Чтобы задать закон движения точки естественным способом необходимо:

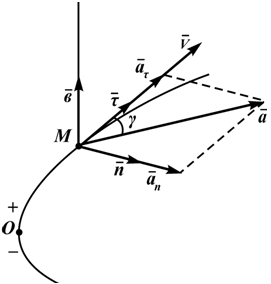
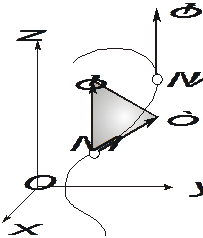
Зная эти параметры можно найти все кинематические характеристики точки в любой момент времени (рисунок 1.5).

Скорость и ускорение точки

Скорость точки при естественном способе задания её движения определяется по формулам

Первая формула определяет величину и направление вектора скорости, вторая формула только величину.

Ускорение определяется как производная от вектора скорости:

оно характеризует быстроту изменения величины скорости точки;

Нормальное ускорение точки

характеризует быстроту изменения направления вектора скорости;

ρ — радиус кривизны траектории в данной точке (например, для окружности: ρ = R, для прямой линии ρ = ∞).

Полное ускорение точки при естественном способе задания движения определяется следующим образом (рисунок 1.5):

Ранее отмечалось, что всегда можно перейти от одного способа задания закона движения точки к другому, например, от координатного к векторному. Поэтому, преобразовывая одни и те же формулы, можно получить другое их написание.

Далее, для естественнго способа задания движения точки, получаем

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.

Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.

В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.

Векторный

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

Координатный

При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.

Естественный

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Естественный способ задания движения точки

Естественным способом задания движения пользуются в тех случаях, когда траектория движущейся точки известна заранее. Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. Если траектория является прямой линией, то движение точки называется прямолинейным, а если кривой линией – то криволинейным.

Координатный способ задания движения точки

В этом случае положение движущейся точки в пространстве определяют тремя ее декартовыми координатами относительно выбранной неподвижной прямоугольной системы (рис. 41). При движении точки эти координаты являются однозначными и непрерывными функциями времени, т.е. уравнения движения получают в виде

, , .

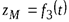
При координатном способе задания движения точки траектория в непосредственном виде не дается, но может быть получена из уравнений движения. Исключая из уравнений движения время, получаем два соотношения между координатами , которые определяют линию, описываемую в пространстве движущейся точкой, т.е. ее траекторию.

При движении точки в плоскости можно пользоваться не только декартовыми координатами. В этом случае можно ввести в рассмотрение полярные координаты (рис. 42).

Положение точки в этом случае будут определять полярными координатами и , т.е. уравнения движения точки вполярных координатах имеют вид .

Векторный способ задания движения точки

В этом случае положение точки в пространстве определяется только радиусом – вектором, проведенным из начала декартовой системы координат (рис. 43). Уравнение движения в этом случае имеет вид

.

25 Как определяется скорость точки при векторном, координатном и естественном

Определение скорости и ускорение точки при векторном задании движения

откуда (1.6)

Направлен вектор скорости по касательной к траектории.

Ускорение в данный момент

откуда (1.7)

Лежит вектор ускорения в плоскости, проведенных через касательной к траектории в двух бесконечно близких точках. Эта плоскость называется соприкасающейся или плоскостью главной кривизны.

Определение скорости и ускорения точки при координатном способе задания движения

при координатном способе задания движения:

Сравнивая (а) и (б) находим:

; ; (1.8)

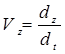
т.е. проекция вектора скорости на оси координат равны первым производным по времени от соответствующих координат.

(1.9)

направление вектора скорости определяется с помощью направляющих косинусов, т.е. косинусов углов между вектором скорости и осями координат (рис. 1.6).

Аналогично ищем ускорения:

Сравнивая (в), (г), (д) находим:

(1.11)

Проекция ускорения равны первым производным по времени от соответствующих проекций скорости или вторым производным по времени от соответствующих координат.

(1.12)

(1.13)

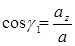
Определение скорости и ускорения точки при естественном задании движения

Пусть за время точка переместилась из положения М в положение М₁, совершив перемещение (рис. 1.17).

величина скорости точки:

(1.14)

Направлена скорость по касательной к траектории:

Найдем ускорение точки.

Пусть в положении М точка имеет скорость (рис. 1.8).

Полное ускорение точки будет:

Обозначим угол между касательными через (угол смежности). Спроецируем вектор ускорения на касательную и нормам п.

Подставив эти значения в а_п получим:

Т.о. величины касательного, нормального и полного ускорений определяется формулами:

Нормальное ускорение направлено по нормам к траектории к центру кривизны и характеризует изменение направления скорости.

a) Определение ускорения при векторном способе задания движения.

Пусть точка М в момент времени t находится в положении М(t) и имеет скорость V(t), а в момент времени t + Dt находится в положении М(t + Dt) и имеет скорость V(t + Dt) (см. рис. 2.9).

Рис. 2.9. Ускорения точки при векторном способе задания движения

.

Предел 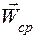при Dt ® 0 называется мгновенным (или просто ускорением) точки М в момент времени t

. (2.11)

Согласно (2.11), ускорение при векторном способе задания движения равно векторной производной от скорости по времени.

б). Ускорения при координатном способе задания движения.

Подставляя (2.6) в (2.11) и дифференцируя произведения в скобках, находим:

.

Учитывая, что производные от единичных векторов равны нулю, получаем:

. (2.12)

Вектор может быть выражен через свои проекции:

. (2.13)

Сравнение (2.12) и (2.13) показывает, что вторые производные от координат по времени имеют вполне определенный геометрический смысл: они равны проекциям полного ускорения на координатные оси, т.e.

, , .

Зная проекции, легко вычислить модуль полного ускорения и направляющие косинусы, определяющие его направление:

, , , . (2.14)

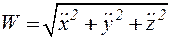
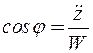
в). Ускорение точки при естественном способе задания движения

Приведем некоторые сведения из дифференциальной геометрии, необходимые для определения ускорения при естественном способе задания движения.

Пусть точка М движется по некоторой пространственной кривой. С каждой точкой этой кривой связаны три взаимно ортогональные направления (касательная, нормаль и бинормаль), однозначно характеризующие пространственную ориентацию бесконечно малого элемента кривой вблизи данной точки. Ниже приводится описание процесса определения указанных направлений.

Рис. 2.10. Определение касательной к траектории движения точки

Касательная к кривой в точке М определяется как предельное положение секущей ММ₁ при стремлении точки М₁ к точке М (рис. 2.10). Единичный вектор касательной принято обозначать греческой буквой .

Проведем единичные векторы касательных к траектории в точках М и М₁. Перенесем вектор в точку М (рис. 2.11) и образуем плоскость, проходящую через эту точку и векторы и . Повторяя процесс образования аналогичных плоскостей при стремлении точки М₁ к точке М, мы получаем в пределе плоскость, называемую соприкасающейся плоскостью.

Рис. 2.11. Определение соприкасающейся плоскости

Очевидно, что для плоской кривой соприкасающаяся плоскость совпадает с плоскостью, в которой лежит сама эта кривая. Плоскость, проходящая через точку М и перпендикулярная касательной в этой точке, называется нормальной плоскостью. Пересечение соприкасающейся и нормальной плоскостей образует прямую, называемую главной нормалью(рис. 2.12).

Дата добавления: 2019-02-22 ; просмотров: 902 ; Мы поможем в написании вашей работы!

Источник

Естественный способ задания движения точки

Содержание:

Естественный способ задания движения точки состоит в том, что в нём задаются: – траектория движения; – начало и положительное направление отсчета; – закон движения точки по траектории.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Естественный способ задания движения точки

Определим сначала кинематическое уравнение движения при натуральном способе задания движения материальной точки.

Натуральный способ задания (описания) движения материальной точки применяется тогда, когда траектория точки заранее известна. Движение изучается относительно фиксированного начала отсчета. Задается и закон движения материальной точки вдоль траектории.

Таким образом, для задания движения натуральным способом необходимо знать:

1. Траекторию АВ (рис. 2.3), которая может быть задана уравнением, графически или указанием, например точка движется вдоль окружности радиусом R.

2. Начало отсчета О криволинейной координаты S на траектории движения с указанием положительных «+» и отрицательных «–» значений. Кроме того, задается начало отсчета времени t. Обычно принимают, что t = 0 в момент, когда точка M проходит через точку O на траектории движения.

3. Закон движения материальной точки вдоль траектории. если, например, в момент времени t точка занимает положение M, криволинейная координата которого равна S, то это записывается следующим образом:

Эта функция должна быть непрерывной и по крайней мере дважды дифференцированной.

Соотношение называется кинематическим уравнением движения материальной точки в натуральной форме (или законом изменения криволинейной координаты). Это фактически расстояние подвижной точки M от начала отсчета вдоль траектории движения.

Криволинейную координату не следует путать с длиной пути, который проходит точка за определенный промежуток времени как в положительном, так и в отрицательном направлениях.

Определим кинематические характеристики движения материальной точки при
натуральном способе задания ее движения.

Скорость движения точки

Рассмотрим схему движения материальной точки M (рис. 2.3). Положение точки М соответствует моменту времени t, а положение М₁ — t₁. Тогда промежутку времени t₁ – t = ∆t соответствует изменение криволинейной координаты S₁ – S = ∆S. Отсюда можно определить среднюю скорость точки за промежуток времени ∆t:

А скорость точки в любой момент времени t можно определить, если взять предел отношения , когда ∆t стремится к нулю:

Модуль скорости материальной точки при натуральном способе задания ее движения равен первой производной по времени от закона движения точки.

Направление вектора скорости — по касательной к траектории движения материальной точки.

Производная по времени определяет численную алгебраическую величину скорости,
то есть, если > 0, то вектор скорости направлен в положительном направлении
отсчета, а если 2 + t м. Определить пройденный путь и скорость движения точки в момент времени t₁ = 1 c.

Решение.

Определим сначала положение точки на траектории движения при t₁ = 1 c. Поскольку отсчет времени начался с началом момента движения, то S(0) = 0. Подставим в уравнение движения значение этого момента времени:

Для определения скорости движения точки продифференцируем по времени уравнения движения:

Из полученной функции скорости движения материальной точки можем определить (подстановкой t), что в начале движения (при t = 0): (0) = 1 м/c, а при t₁ = 1 c; (1) = 9 м/c.

Переход от координатного способа задания движения материальной точки к натуральному

Для перехода от одного способа задания движения материальной точки к другому необходимо найти зависимости между основными параметрами этих движений. Сделаем это, рассматривая координатный и натуральный способы задания движения материальной точки. Так, на основании уравнения, что определяет скорость материальной точки при натуральном способе задания ее движения, можно записать

dS = · dt,

Поскольку при координатном способе задания движения материальной точки ее скорость определяется согласно выражению:

то, подставляя его в предыдущее выражение, окончательно найдем зависимость между двумя указанными способами задания движения материальной точки:

Натуральный трехгранник

Приведем некоторые сведения из дифференциальной геометрии, которые понадобятся для определения кинематических характеристик движения материальной точки.

Предположим, что кривая АВ является траекторией точки М (рис. 2.4). В произвольной точке М и в бесконечно приближенной к ней точке М₁ проведем касательные этой кривой (орты, подходящие этим касательным, обозначим через и ₁). Затем перенесем вектор ₁ параллельно самому себе в точку М и проведем через векторы и ₁ плоскость Q.

Плоскость, которая является предельным положением плоскости Q, когда точка M,
направляется к точке M, называется соприкасающихся плоскостью.

Через точку М проведем плоскость, перпендикулярную к касательной , которая называется нормальной. Очевидно, что любая прямая в этой плоскости, проходящей через точку M, будет перпендикулярна к , то есть будет нормалью к кривой.

Линия пересечения нормали и стычной плоскостей определяет главную нормаль к кривой. Итак, главная нормаль — это единственная из бесконечного множества нормалей к кривой в точке M, которая расположена в соприкасающейся плоскости. Плоскость, проходящая через точку M перпендикулярна главной нормали, называется спрямляющей.

Линия пересечения спрямляющей и нормальной плоскостей определяет бинормаль
кривой. Очевидно, что бинормаль перпендикулярна к главной нормали.

Таким образом, в каждой точке кривой можно указать три взаимно перпендикулярные направления, по которым можно провести касательную в сторону роста дуговой координаты (соответствующий орт ), главную нормаль — в сторону вогнутости кривой (соответствующий орт ), бинормаль с соответствующим ортом , направленную так, что орты , , образуют правую ортогональную тройку векторов.

Прямоугольная подвижная система координатных осей с ортами , и , с началом в подвижной точке M называется системой натуральных осей, или натуральным подвижным трехгранником M .

Заметим, что плоская кривая полностью расположена в соприкасающейся плоскости, а главная нормаль является нормалью к кривой в этой плоскости. В отличии от других систем отсчета, натуральный трехгранник движется вместе с точкой и меняет свою ориентацию в пространстве в соответствии с характером траектории.

Кривизна кривой

Как видно дальше, ускорение точки в криволинейном движении зависит от кривизны траектории, поэтому рассмотрим эту характеристику. На рис. 2.5 изображена траектория AB движения точки и два близких положения M и M₁. Проведем через точки M и M₁ касающиеся и ₁. Элементарное расстояние между точками M и M₁ вдоль траектории равно ∆S.

Угол ∆φ между касательными в двух близких точках является углом смежности.

Кривизной кривой К в данной точке М называется предел отношения угла смежности к дуге ∆S, его взимает, когда эта дуга стремится к нулю.

Если, отношение ∆φ к ∆S является средней кривизной:

то, возведение K_c до границы дает истинное значение кривизны кривой:

Рассмотрим круг радиусом R (рис. 2.6). сделаем аналогичное геометрическое построение. Выразим ∆S по известной формуле:

и подставим в предыдущую формулу. Будем иметь:

K = .

Таким образом, круг радиусом R является кривой постоянной кривизны, значение которой равно обратной величине радиуса.

Для определения кривизны произвольной кривой достаточно подобрать такой круг, элемент дуги которого лучше всего аппроксимирует участок кривой в данной точке.

Тогда радиус круга будет радиусом кривизны кривой, а центр круга — центром кривизны.

Это показано на рис. 2.5:

K₂ = — кривизна кривой в точке M₂.

Касательное и нормальное ускорения точки в натуральных осях координат

В декартовых осях координат мы определяли ускорение точки в проекциях на оси x, y, z. В натуральных осях координат определим проекции вектора ускорения на касательную и главную нормаль n. Но сначала докажем, что проекция вектора ускорения на бинормаль b
равна нулю. Обратимся к рис. 2.7. Скорости близких точек M и M₁ — векторы и , которые направлены по касательным и ₁ в этих точках.

Перенесем параллельно вектор в точку M и соединим концы векторов и . Построив параллелограмм, можно увидеть, что вектор ∆, как разница скоростей, формирует вектор ускорения и расположен в соприкасающейся плоскости.

Параллельно ∆ направлен и вектор среднего ускорения , а вектор ускорения в данный момент времени равен:

и также будет расположен в соприкасающейся плоскости. А это значит, что проекция
вектора ускорения на бинормаль равна нулю.

Теперь, зная, что вектор ускорения имеет только касательную и нормальную составляющие, определим остальные.

Для этого нам понадобится схема, представленная рис. 2.8, где:

M — касательная к траектории,

M n — главная нормаль,

C — центр кривизны траектории,

ρ — радиус кривизны траектории.

Предположим, что в момент времени t точка M имеет скорость , а в момент t₁ = t + ∆t — скорость . Тогда ускорение будет равно:

Переходим к проекциям ускорения материальной точки на натуральные оси координат и n:

Учитывая, что проекции векторов на параллельные оси одинаковы, проведем через точку М₁ оси М₁´ и М₁ n´, которые параллельные соответствующим осям M и M n, и обозначим угол смежности ∆φ.

Найдем проекции векторов и на оси M и M n:

Подставим значения проекций в выражения. Будем иметь:

Когда промежуток времени Δt стремится к нулю, то

Тогда уравнение может быть записано, как показано ниже, и касательное ускорение равно:

Таким образом, касательное ускорение материальной точки характеризует изменение скорости по величине в единицу времени и равна первой производной от функции скорости по времени или второй производной от закона движения.

Определим нормальное ускорение a_n. Преобразуем выражение для нормального ускорения, умножив числитель и знаменатель на произведение ∆φ · ∆S:

Перепишем выражение следующим образом:

Подставим значение этих границ в выражение для нормального ускорения:

Нормальное ускорение материальной точки характеризует изменение скорости по направлению в единицу времени и равна квадрату скорости, разделенном на радиус кривизны траектории в данной точке.

Вектор нормального ускорения всегда направлен вдоль нормали к центру кривизны в данной точке.

Вектор полного ускорения может быть определен геометрическим сложением векторов и и является диагональю прямоугольника построенного на указанных векторах, как на сторонах (рис. 2.9). Модуль полного ускорения a равен:

Угол φ между вектором и нормалью n определяется тригонометрически:

Вектор ускорения через его проекции a и a_n может быть записан следующим образом:

= a · + a_n · ,

где , — соответствующие орты касательной и нормали натуральных осей координат.

Следует отметить, что составляющие вектора вдоль натуральных осей координат равны:

Некоторые случаи движения материальной точки

1. Прямолинейное движение.

Радиус кривизны траектории, которой является прямая линия, равна = ∞, поэтому:

Таким образом, скорость движения материальной точки изменяется только численно, по модулю. Это означает, что имеет отношение ускорения a характеризует изменение вектора скорости по модулю.

А если это движение еще и равномерно, то есть, когда = const, то ускорение материальной точки будут равно:

2. Равномерное криволинейное движение.

В данном случае модуль скорости = const, а радиус кривизны траектории ≠ ∞. Определим ускорение a движения материальной точки:

Таким образом, как видно из приведенных выражений, полное ускорение a материальной точки в этом случае равно нормальному ускорению a_n.

Вектор нормального (в данном случае полного) ускорения направленный по нормали к траектории движения частицы. Поскольку ускорение a появляется только за счет изменения направления вектора скорости , то нормальное ускорение a_n характеризует изменение вектора скорости по направлению.

3. Равнопеременное криволинейное движение.

В этом случае движение точки является криволинейным, но ускорение a есть
величиной постоянной. Этот случай носит название равнопеременного движения (то есть, когда за равные промежутки времени скорость движения материальной точки изменяется на одну и ту же величину, увеличивается или уменьшается).

Определим кинематические характеристики равнопеременного движения материальной точки. Поскольку a = const, а a = , то отсюда есть возможность определить скорость движения точки:

dv = a · dt.

Скорость находится под знаком дифференциала, поэтому для ее определения необходимо взять интегралы от левой и правой частей последнего выражения. Используем для этого определенные интегралы, для которых задаем верхнюю и нижнюю границы переменных величин. Скорость точки меняется от начального значения _o к конечному , а время от начала отсчета t = 0 до конечного t:

– _o = at,

= _o + at,

где _o — начальная скорость движения материальной точки.

Используем далее выражение с которого есть возможность определить dS. Перемещение будет равно:

Вместо подставим в последнее выражение полученное его значение:

dS = _odt + atdt.

Как и в предыдущем случае найдем перемещения S, взяв определенные интегралы от левой и правой частей последнего выражения. Также задаем верхние и нижние границы переменных величин, причем перемещение точки изменяется от начального значения S_o до конечного S:

Окончательно последнее выражение можно переписать так

где S_o — начальное перемещение точки.

Таким образом, при равнопеременном движении материальной точки ее скорость и перемещения определяются с помощью найденных выражений. Следует заметить, что знаки в правых частях этих формул (перед a) определяют характер равнопеременного движения. Так, если они положительные, то движение точки является равноускоренным, а если отрицательные, то — равнозамедленным.

Пример:

Палец кривошипа дизеля движется в соответствии заданных параметрически уравнений

Определить траекторию движения, скорость и ускорение пальца.

Решение.

Для определения уравнения траектории движения пальца кривошипа надо исключить из заданных уравнений движения параметр времени t. Сначала определим с заданных уравнений тригонометрические функции

Поскольку тригонометрические функции являются функциями одного аргумента, то
поднимем к квадрату левые и правые части этих выражений и добавим их почленно:

Левая часть последнего выражения равна единице, поскольку sin cos 1 2 февраля t  t , тогда sin 2 ω t + cos 2 ω t = 1, тогда

Таким образом, с последнего выражения видно, что траекторией движения пальца кривошипа является окружность радиуса b с центром в начале координат.

Для определения скорости движения найдем сначала проекции скорости движения пальца на координатные оси:

Модуль скорости движения будет равняться

Таким образом, с последнего выражения видно, что палец движется с постоянной скоростью, равной bω.

Найдем ускорение пальца кривошипа. Также определим его через проекции на оси координат. Для этого возьмем другие производные от заданных координат движения:

Полное ускорение будет равно:

Поскольку палец кривошипа движется по кругу, то есть по криволинейной траектории движения устойчивого радиуса b, то его ускорение можно было бы определить, если использовать выражения, описывающие натуральный способ задания движения материальной точки. Касательное ускорение пальца кривошипа будет равняться нулю, поскольку скорость bω = const. А именно:

Нормальное ускорение определим так:

Поскольку касательного ускорения нет, то полное ускорение равно нормальному:

Таким образом, как видим, ускорение пальца кривошипа, которое определено различными способами, совпадают.

Пример:

Точка на ободе барабана зерноуборочного комбайна в период разгона движется согласно уравнению S = 0,1 · t 3  (S — в метрах, t — в секундах). Радиус барабана равен R = 0,5 м. Определить касательное и нормальное ускорение точки в момент, когда его скорость равна = 30 м/с.

Решение.

Уравнения движения точки задано натуральным способом, а потому скорость можно определить так:

По заданному значению скорости под углом = 30 м/с найдем время. Подставим значение этой скорости в полученное выражение и найдем t:

Касательное ускорение точки будет равно:

Нормальное ускорение определим так:

Знак «+» перед касательным ускорением a означает, что барабан зерноуборочного комбайна находится в состоянии разгона, что соответствует условию задачи.

Услуги по теоретической механике:

Учебные лекции:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник