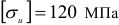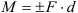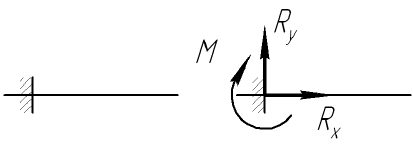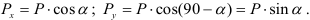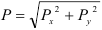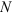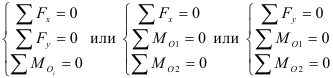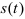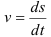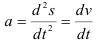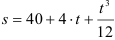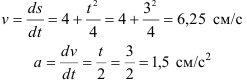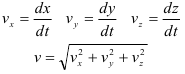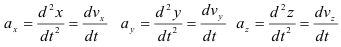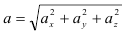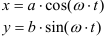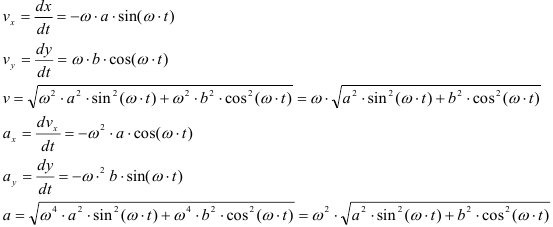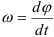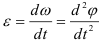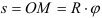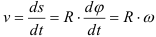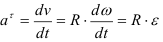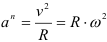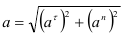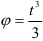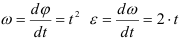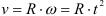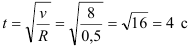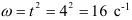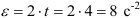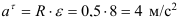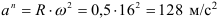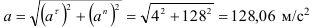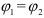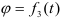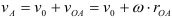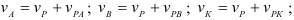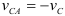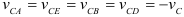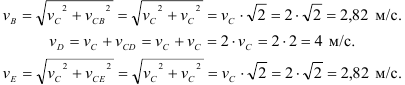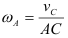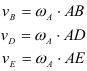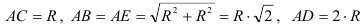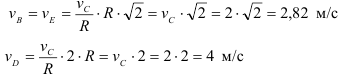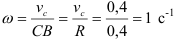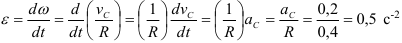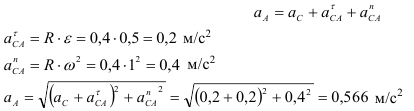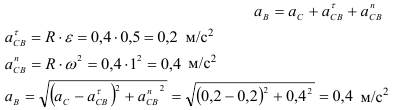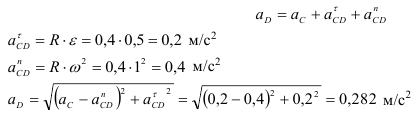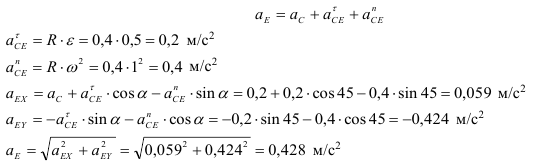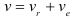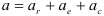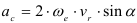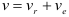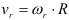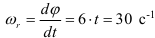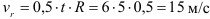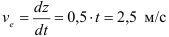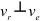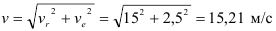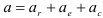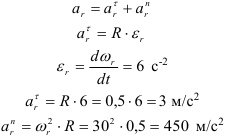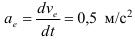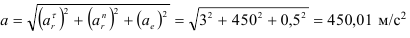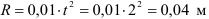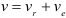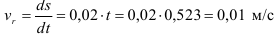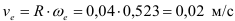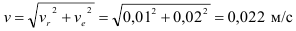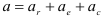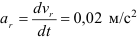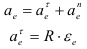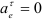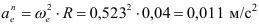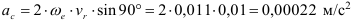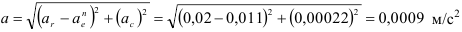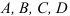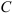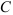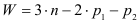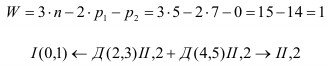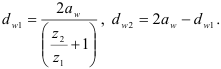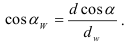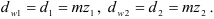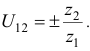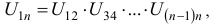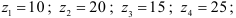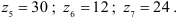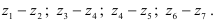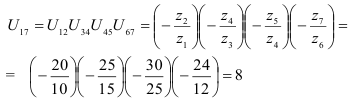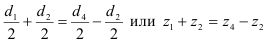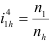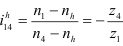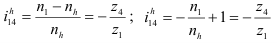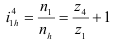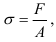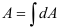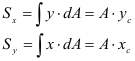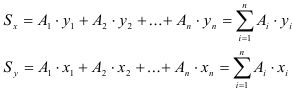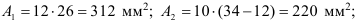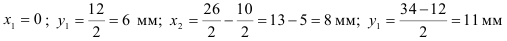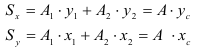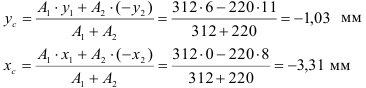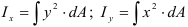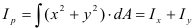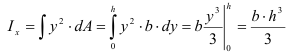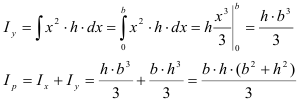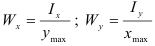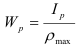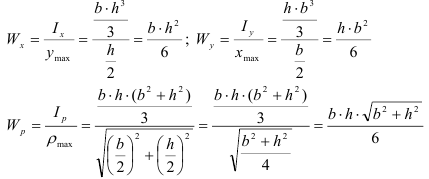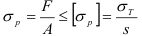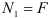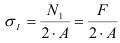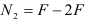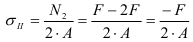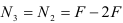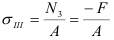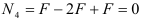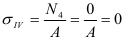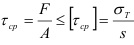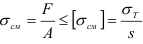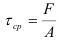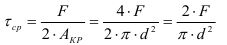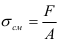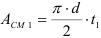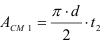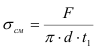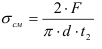Что не является разделом технической механики
iSopromat.ru
Техническая механика (сокр. — техмех) — часть общей механики, изучающая механическое движение и различные виды взаимодействия материальных тел.
Курс технической механики состоит из разделов:
Для изучения данного курса и успешной сдачи экзаменов на нашем сайте Вы можете:
Содержание разделов технической механики
Лекции по технической механике не вошедшие в данный список можно найти, пройдя по ссылке на соответствующий раздел или воспользовавшись поиском по сайту.
Теоретическая механика
Кинематика
Статика
Динамика
Сопротивление материалов
Теория механизмов и машин
Детали машин
Цели освоения предмета «Техническая механика»
Целью освоения дисциплины «Техническая механика» является обобщение знаний механических дисциплин, необходимых для расчета и конструирования простейших деталей механизмов, приборов, и формирование фундамента для изучения дисциплин профессионального цикла, а также последующего обучения в магистратуре, аспирантуре.
Задания, выдаваемые для самостоятельной работы, способствуют развитию умения пользоваться типовыми методами расчета и проектирования машин.
В сумме со всеми предшествующими дисциплинами «Техническая механика» является завершающим курсом в подготовке бакалавров технологических специальностей.
В результате освоения дисциплины «Техническая механика» студент должен:
Место техмеха в структуре ООП ВПО
Дисциплины, предшествующие изучению данной дисциплины: «Высшая математика», «Физика», «Инженерная графика», «Информатика».
Предметы, для которых освоение данной дисциплины необходимо как предшествующее: «Надежность технических систем и техногенный риск» и другие специальные дисциплины.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Основные определения и понятия технической механики
Основные определения и понятия технической механики.
1. Теоретическая механика – это наука о равновесии тел в пространстве, о системах сил, и о переходе одной системы в другую.
2. Сопротивление материалов – наука о расчетах конструкций на прочность, жесткость и устойчивость.
3. Детали машин – это курс, изучающий назначение, классификацию и основы расчета деталей общего типа.
Механические движения – это изменение положения тела в пространстве и во времени.
Материальная точка – это тело, формами и размерами которого можно пренебречь, но которое обладает массой.
Абсолютно твердое тело – это тело, у которого расстояние между любыми двумя точками остается неизменным при любых условиях.
Сила – мера взаимодействия тел.
Сила – векторная величина, которая характеризуется:
1. точкой приложения;
2. величиной (модулем);
1. Изолированная точка – это материальная точка, которая под действием сил движется равномерно прямолинейно, либо находится в состоянии относительного покоя.
2. две силы равны, если они приложены к одному телу, действуют вдоль одной прямой и направлены в противоположные стороны, такие силы называются уравновешивающими.
3. Не нарушая состояния тела к нему можно приложить или от него отбросить уравновешивающую систему сил.
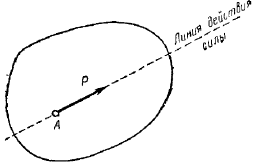
Следствие: всякую силу можно переносить вдоль линии её действия, не изменяя действия силы на данное тело.
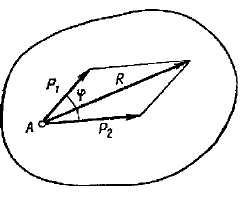
4. Равнодействующая двух сил приложенных в одной точке, приложена в той же точке и является по величине и направлению диагональю параллелограмма, построенных на данных силах.
5. Всякому действию есть равное по величине и направлению противодействие.
Связи и их реакции.
Свободное тело – это такое тело, перемещение которого в пространстве ничего не меняет.
Те тела, которые ограничивают перемещение выбранного тела называются связями.
Силы, с которыми связь удерживают тело называются реакциями связей.
При решении задач мысленно связи отбрасываются и заменяются реакциями связей.
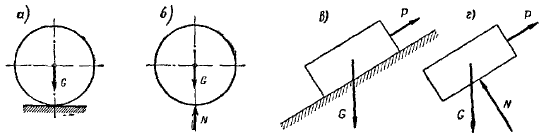
1. Связь в виде гладкой поверхности
3. Связь в виде жесткого стержня.
4. Опора в точке или опора углу.
5. Шарнирно подвижная опора.
6. Шарнирно неподвижная опора.
Система сил – это совокупность.
Сходящиеся Параллельные Сходящиеся Параллельные
Плоская система сходящихся сил.
Плоская система сходящихся сил – это система сил линии действия, которых сходятся в одной точке называются сходящимися.
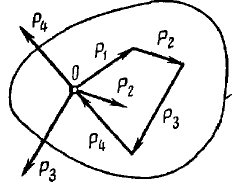
Пусть дана система сходящихся сил F1, F2, F3, линии, действия которых сходятся в точке О. для того, чтобы заменить эту систему сил равнодействующей силой необходимо:
1. Перенести силы в точку О (на основании следствия из аксиом).
2. Почленно сложить вектора сил (на основании аксиомы 4). Равнодействующая всегда направлена из начала первого вектора в конец последней. В результате векторного сложения образуется силовой многоугольник.
Плоская система сходящихся сил имеет два условия равновесия:
1. Геометрическое условие: плоская система сходящихся сил находится в равновесии, если силовой многоугольник замкнут, т. е. равнодействующая равна нулю.
2. Аналитическое условие: плоская система сходящихся сил находится в равновесии если алгебраические суммы проекций всех сил системы на оси х и у равны нулю.
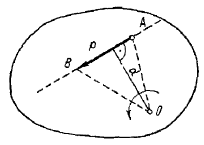
Пара сил – это система двух равных сил, лежащих на параллельных прямых и направленных в противоположные стороны.
Действие пары на тело определяется моментом на пару.
Момент – это произведение модуля силы на плечо.
Плечо – кратчайшее расстояние между линиями действия силы.
Если пара поворачивает плечо по ходу часовой стрелки, то момент считается положительным, а если против хода, то отрицательным.
Пара сил обладает свойствами:
1. не нарушая действия пары на тело можно её переносить в любую точку плоскости.
2. Две пары сил являются эквивалентными, если их моменты равны.
Система пар сил находится в равновесии, если сумма моментов всех пар системы равно нулю.
Произвольная плоская система сил.
Момент силы относительно точки.
Плечо – это кратчайшее расстояние от выбранной точки до линии действия силы.
Момент силы относительно точки может быть равен нулю, если сила проходит через выбранную точку.
Между моментом пары и моментом силы есть разница: момент пары есть величина постоянная, а момент силы относительно точки по знаку зависит от выбора точки.
Три формы равновесия произвольной плоской системы сил.
1. Произвольная плоская система сил находится в равновесии, если алгебраические суммы проекций всех сил на оси х и у равны нулю, а также равна нулю сумма моментов всех сил относительно любой точки.
2. Произвольная плоская система сил находится в равновесии, если алгебраические суммы проекций всех сил на одну из осей х или у равна нулю, а также, если равны нулю алгебраические суммы моментов всех сил относительно любых двух точек.
3. Произвольная плоская система сил находится в равновесии, если алгебраические суммы моментов всех сил относительно любых трех точек, не лежащих на одной прямой.
Пространственная система сил.
Пространственная система сил – это система сил, как угодно расположенных в пространстве.
Суммой трех сил, сходящихся в одной точке является сила по величине и направлению, совпадающая с диагональю параллелепипеда, построенного на заданных силах.
Момент силы относительно оси равен произведению модуля силы на кратчайшее расстояние от выбранной оси до линии действия силы.
Момент может равняться нулю, если:
1. Сила лежит на выбранной оси.
2. Сила пересекает выбранную ось.
3. Сила параллельна оси.
При приведении пространственной системы сил к точке, её можно заменять на эквивалентную систему с главным вектором и главным моментом.
Главный вектор – это геометрическая сумма всех сил системы.
Главный момент – это сумма моментов, компенсирующих пар.
Пространственная система сил находится в равновесии, если алгебраические суммы проекций всех сил на оси x, y, z равны нулю, а также равны нулю моменты всех сил относительно этих же осей.
Кинематика изучает виды движения.
Плоско – параллельное движение.
Плоско – параллельное движение – это такое движение, при котором фигура полученная пересечением данного тела с выбранной плоскостью остается параллельной самой себе за все время движения.
При плоско – параллельном движении всегда существует точка, абсолютная скорость которой в данный момент времени равна нулю. Каждый последующий момент – это будет другая точка.
Динамика изучает виды движения тела в зависимости от приложенных сил.
1. всякая изолированная точка находится в состоянии относительного покоя, или равномерного прямолинейного движения до тех пор, пока приложенные силы не выведут её из этого состояния.
2. Ускорение тела прямопропорциональных действующей на тело силе.
3. Если на тело действует система сил, то его ускорение будет складываться из тех ускорений, которые бы тело получало от каждой силы в отдельности.
4. Всякому действию есть есть равное по величине и противоположно направлению противодействие.
Центр тяжести – это точка приложения силы тяжести, при повороте тела центр тяжести не меняет своего положения.
Сила инерции – всегда направлена в противоположную сторону ускорению и приложена к связи.
При равномерном движении, т. е. когда а=0 сила инерции равна нулю.
При криволинейном движении раскладывается на две составляющие: на нормальную силу и на касательную.
Метод кинематики: условно прикладывают к телу силу инерции можно считать, что внешние силы реакции связей и сила инерции образуют уравновешенную систему сил. F+R+Pu=0
Трение делится на два вида: трение скольжения и трение качения.
Законы трения скольжения:
1. Сила трения прямопропорциональной нормальной реакции опоры и направлена вдоль соприкасающихся поверхностей в противоположную сторону движению.
2. Коэффициент трения покоя всегда больше коэффициента трения движения.
3. Коэффициент трения скольжения зависит от материала и физически – механических свойств трущихся поверхностей.
Трение приводит к снижению срока службы деталей к их износу и нагреву. Для того, чтобы этого избежать необходимо вести смазку. Повысить качество обработки поверхности деталей. В трущихся местах применять другие материалы.
4. По возможности заменить трение скольжения трением качения.
Сопротивление материалов – это наука, изучающая методы расчета конструкций на прочность, жесткость и устойчивость.
Прочность – это способность конструкции выдерживать заданную нагрузку в течение срока службы без разрушения и появления остаточных деформаций.
Жесткость – это способность конструкции сохранять первоначальную форму упругого равновесия.
Устойчивость – это способность конструкции сохранять первоначальную форму упругого равновесия.
Все тела разделены на 3 группы:
1. Брус – это тело, один из размеров которого (длина) во много раз больше двух других.
2. Оболочка – это тело, один из размеров которого (толщина) во много раз больше двух других.
3. Массив – это тела, все размеры которого равны.
1. По характеру действия:
2. По способу приложения:
Мысленно разрезаем нагруженный силами груз, для того, чтобы определить внутренние силовые факторы, для этого отбрасываем одну часть груза. Заменяем межмолекулярную систему сил эквивалентной системой с главным вектором и главным моментом. При разложении главного вектора и главного момента по осям x, y, z. устанавливаем вид деформации.
Внутри сечения бруса может возникать внутри силовых факторов, если возникает сила N (продольная сила), то брус растянут или сжат.
Если возникает Мк (крутящий момент) то деформация кручения, сила Q (поперечная сила) то деформация сдвига среза или изгиба. Если возникает Мих и Миz (изгибающий момент) то деформация изгиба.
Метод сечения позволяет определить напряжение в сечении груза.
Напряжение – это величина, показывающая, сколько нагрузки приходится на единицу площади сечения.
Эпюра – это график изменения продольных сил, напряжений, удлинений, крутящих моментов и т. д.
Растяжение (сжатие) – это такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила.
Правила знаков для нагрузки.
Если нагрузка направлена от сечения бруса, то продольная сила будет равна ей со знаком «плюс», если нагрузка направлена к сечению, то продольная сила будет со знаком «минус».
В пределах упругих деформаций нормальное напряжение прямо – пропорционально продольным деформациям.
Е – модуль Юнка, коэффициент, который характеризует жесткость материала при напряжениях, зависит от материала, образца из справочных таблиц.
Нормальное напряжение измеряется в Паскалях.
Расчет на прочность.
np – расчетный коэффициент запаса прочности.
[n] – допустимый коэффициент запаса прочности.
бmax – расчет максимального напряжения.
Кручение – такой вид деформации, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор – крутящий момент. Кручению повергаются валы, оси. И пружины. При решении задач строятся эпюры крутящих моментов.
Механика
Механика является одним из разделов физики. Под механикой обычно понимают классическую механику. Механика – наука, изучающая движение тел и происходящие при этом взаимодействия между ними.
В частности, каждое тело в любой момент времени занимает определенное положение в пространстве относительно других тел. Если со временем тело меняет положение в пространстве, то говорят, что тело движется, совершает механическое движение.
Механическим движением называется изменение взаимного положения тел в пространстве с течением времени.
Основная задача механики – определение положения тела в любой момент времени. Для этого нужно уметь кратко и точно указать, как движется тело, как при том или ином движении изменяется его положение с течением времени. Другими словами – найти математическое описание движения, т. е. установить сязи между величинами, характеризующими механическое движение.
При изучении движения материальных тел используют такие понятия, как:
Классическая механика основана на принципе относительности Галилея и законах Ньютона. Поэтому, ее еще называют – механикой Ньютона.
Механика изучает движение материальных тел, взаимодействия между материальными телами, общие законы изменения положений тел со временем, а также причины вызывающие эти изменения.
Общие законы механики подразумевают, что они справедливы при изучении движения и взаимодействия любых материальных тел (кроме элементарных частиц) от микроскопических размеров до объектов астрономических.
Механика включает в себя следующие разделы:
Следует отметить, что это не все разделы, которые входят в механику, но это основные разделы, которые изучает школьная программа. Кроме разделов указанных выше существует еще ряд разделов как имеющих самостоятельное значение, так и тесно связанных между собой и с указанными разделами.
Появление дополнительных разделов связано как с выходом за границы применимости классической механики (квантовая механика), так и с детальным изучением явлений происходящих при взаимодействии тел (например, теория упругости, теория удара).
Но, несмотря на это, классическая механика не теряет своего значения. Она является достаточной для описания в широком диапазоне наблюдаемых явлений без необходимости обращаться к специальным теориям. С другой стороны она проста для понимания и создает базу для других теорий.
Механика имеет большое значение для многих разделов астрономии, особенно для небесной механики (где изучаются движения планет, звезд и т. д.).
Особое значение механика имеет для техники. В гидродинамике, аэродинамике, динамике машин и механизмов, теории движения наземных, воздушных и транспортных средст используют уравнения и методы теоретической механики.
iSopromat.ru
Теоретическая механика
Теоретическая механика (сокр. — теормех, термех) — наука, изучающая законы движения, равновесия и механических взаимодействий материальных тел.
Курс теоретической механики состоит из трёх разделов: кинематики, статики и динамики.
О предмете
Теормех — первый раздел технической механики, в котором рассматриваются общие законы механических взаимодействий между материальными телами, а также общие законы движения тел по отношению друг к другу.
Механическое взаимодействие между материальными телами является простейшим и одновременно самым распространенным видом взаимодействия между физическими объектами. Механическое движение, будучи самым простым видом движения, является фундаментальным свойством материи.
Основные разделы теоретической механики
Теоретическая механика, преподаваемая в техническом вузе, содержит три раздела: кинематику, статику и динамику.
Объекты и цель изучения
Целью изучения дисциплины «Теоретическая механика» является формирование необходимой базы знаний для изучения других технических дисциплин по профилю будущей профессиональной деятельности, таких как сопротивление материалов и теория механизмов и машин.
В разделах теоретической механики изучаются общие законы движения и равновесия материальных систем; исследуются простейшие логические модели, на которые могут быть разложены объекты техники и природы, дается научный метод познания законов механического движения систем.
Задачи курса теоретической механики
Задачами курса теоретической механики являются:
Учебные материалы по теормеху
На нашем сайте Вы можете просмотреть и использовать для изучения курса теоретической механики следующие учебные материалы:
Другие разделы механики:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Техническая механика
Здравствуйте, на этой странице я собрала краткий курс лекций по предмету «Техническая механика».
Лекции подготовлены для студентов любых специальностей и охватывают полностью предмет «техническая механика».
В лекциях вы найдёте основные законы, теоремы, правила и примеры.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Введение в техническую механику
Техническая механика — это наука, в которой изучаются общие законы механического движения и механического взаимодействия материальных тел.
Механическим движением — называется перемещение тела но отношению к другому телу, происходящее в пространстве и во времени.
Курс технической механики делится на три раздела: статику, кинематику и динамику.
Статика
Статикой называется раздел механики, в котором изучаются методы преобразования систем сил в эквивалентные системы и устанавливаются условия равновесия сил, приложенных к твердому гелу.
Классификации нагрузок
Важнейшим понятием технической механики является понятие нагрузки.
Взаимодействие двух тел, способное изменить их кинематическое состояние, назы вается меха ни ческим взаимодействием.
Нагрузка — это мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия.
В механике встречается два вида нагрузки
Сила определяется тремя элементами: числовым значением (модулем), направлением и точкой приложения.
Сила изображается вектором. Прямая, по которой направлена данная сила, называется линией действия силы. За единицу силы в Международной системе единиц измерения СИ (в механике система МКС) принимается ньютон 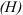
Моментом силы относительно некоторой точки на плоскости называется произведение модуля силы на ее плечо относительно этой точки, взятое со знаком плюс или минус:
Плечом силы 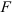
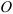
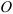
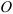
Момент силы относительно точки считается положительным, если сила 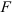
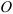
Система двух равных по модулю, параллельных и противоположно направленных сил 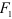
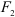
Расстояние 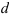
По характеру погружения
По характеру воздействия на тело
По характеру изменения нагрузки во времени
По форме возникновения
Классификации опор (реакции связей)
Твердое тело называется свободным, если оно может перемещаться в пространстве в любом направлении.
Тело, ограничивающее свободу движения данного твердого тела, является по отношению к нему связью.
Твердое тело, свобода движения которого ограничена связями, называется несвободным.
Реакцией связи называется сила или система сил, выражающая механическое действие связи на тело
Одним из основных положений механики является принцип освобождаем ост и твердых тел от связей, согласно которому несвободное твердое тело можно рассматривать как свободное, па которое, кроме задаваемых сил, действуют реакции связей.
Классификация реакций связей (реакций опор)
Реакция гладкой плоскости 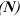
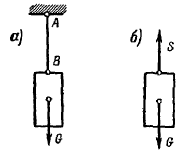
Реакция гибкой связи 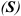
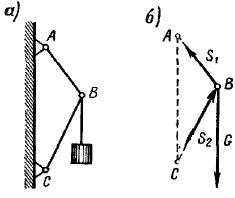
Реакция жесткой связи 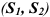
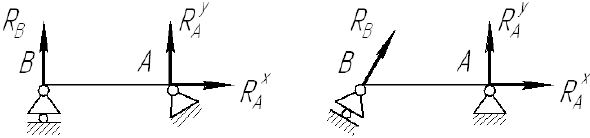
Реакция шарнирно-подвижной опоры 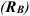
Направление реакции шарнирно-неподвижной опоры зависит от внешних сил, приложенных к системе. Данную реакцию задают двумя составляющими 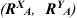
Данную реакцию задают двумя составляющими, направленными перпендикулярно друг к другу и парой сил.
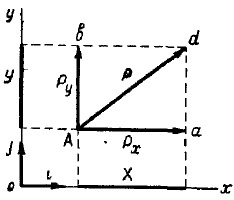
Проекции сил на оси
Взяв две взаимно перпендикулярные оси 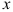
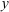
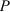
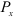
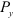
Силы 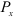
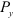
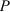
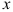
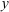
Проекция силы на ось определяется произведением модуля силы на косинус угла между направлениями оси и силы.
Если известны проекции силы на две взаимно перпендикулярные оси 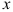
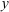
Сходящиеся силы. Условие равновесии системы сходящихся сил
Если к телу приложены несколько сил, линии действия которых пересекаются в одной точке то такие силы называются сходящимися.
Если к телу приложено несколько сил, то данные силы можно заменить одной силой, называемой равнодействующей, под действием которой тело будет находится в нагруженном состоянии эквивалентном заданной системе.
Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.
Сходящиеся силы уравновешиваются в том случае, если их равнодействующая равна нулю, т. е. многоугольник сил замкнут.
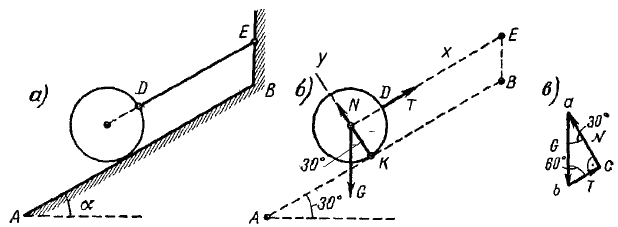
Пример:
Известно 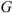
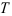
Спроектируем на ось 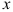
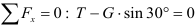
Спроектируем на ось 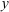
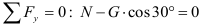
Условии равновесии статически определимых систем (уравнение проекций сил на оси и уравнение моментов)
Тело находится в равновесии, если сумма проекций, действующих на него сил на координатную ось равны 0.
Тело находится в равновесии, если сумма моментов сил относительно какой либо точки этого тела равны 0.
Для любого тела можно составить три уравнения равновесия
Статически определимой системой называется система, в которой число неизвестных не превышает числа уравнений равновесия.
Пример:
Пример:
Кинематика
Кинематикой называется раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение.
Определение скорости и ускорении точки
Скорость — это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.
Ускорение точки — векторная величина, характеризующая быстроту изменения модуля и направления скорости точки.
Задание скорости и ускорения точки естественным способом
При задании точки естественным способом известен закон движения, выраженный зависимостью перемещения точки от времени
В этом случае скорость точки будет определяться как первая производная от данной зависимости
Ускорение точки будет определяться как вторая производная от зависимости перемещения или как первая производная от зависимости скорости
Пример:
Точка движется по окружности радиусом 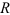
Определить скорость и ускорение точки в конце 3 секунды
Задание скорости точки координатным способом
При задании точки координатным способом известны законы изменения координат данной точки в зависимости от времени 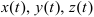
В этом случае скорость точки будет определяться как геометрическая сумма первых производных от данных зависимостей
Ускорение точки будет определяться как геометрическая сумма первых производных от зависимостей скорости или вторых производных от зависимости изменения координат
Пример:
Уравнения движения точки имеют вид
Определить уравнения скорости и ускорения данной точки
Если направление ускорения совпадает с направлением скорости (имеет одинаковый знак) то тело движется с положительным ускорением (ускоряется), если направление ускорения не совпадает с направлением скорости (имеет разные знаки) то тело движется с отрицательным ускорением (замедляется)
Поступательное движение
Поступательным движением твердого тела называется такое движение, при котором любая прямая, соединяющая две точки тела, движется параллельно самой себе.
Все точки твердого тела, движущегося поступательно, описывают тождественные и параллельные между собой траектории и в каждый момент времени имеют геометрически равные скорости и ускорения.
Уравнениями поступательного движения твердого тела являются уравнения движения любой точки этого тела — обычно уравнения движения его центра тяжести 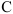
Для описания скорости и ускорения точки используются зависимости рассмотренные в предыдущем вопросе.
Вращательное движение
Вращательным называется такое движение твердого тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения.
При этом движении все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на этой
Аналогом перемещения во вращательном движении является угол поворота 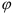
Величина, характеризующая быстроту изменения угла поворота с течением времени, называется угловой скоростью тела.
Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением тела.
Вращение тела, при котором угловое ускорение постоянно, называют равнопеременным вращением. При этом, если абсолютная величина угловой скорости увеличивается, вращение называют равноускоренным, а если уменьшается равнозамедленным.
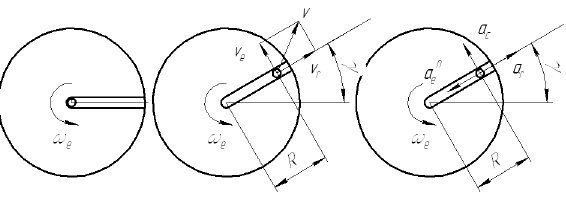
Рассмотрим движение точки 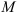
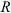
Обозначим точку отсчета 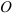
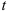
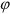
За время 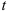
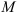
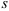
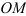
Скорость точки 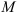
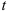
Величина окружной скорости определяется из выражения.
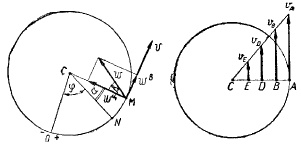
Из предыдущей формулы следует, что модули окружных скоростей различных точек вращающегося тела пропорциональны расстояниям от этих точек до оси вращения.
Ускорение точки 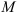
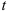
Тангенциальное ускорение направлено по касательной к окружности в точке 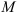
Нормальное ускорение направлено по радиусу окружности к её центру. Величина нормального ускорения определяется по зависимости
Полное ускорение точки определится из выражения
Пример:
Вращение маховика в период пуска машины определяется уравнением
где 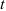
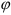
По уравнению вращения маховика находим его угловые скорость и ускорение
Определяем уравнение окружной скорости точки
Выражаем отсюда время
Угловая скорость
Угловое ускорение
Тангенциальное ускорение
Нормальное ускорение
Полное ускорение
Возможно эта страница вам будет полезна:
Плоскопараллельное движение
Плоскопараллельным движением твердого тела называется такое движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости.
Так как положение плоской фигуры на плоскости вполне определяется положением двух ее точек или положением отрезка, соединяющего две точки этой фигуры, то движение плоской фигуры в ее плоскости можно изучать как движение прямолинейного отрезка в этой плоскости.
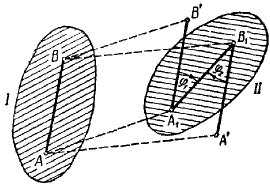
Предположим, что плоская фигура переместилась на плоскости из положения I в положение II. Отметим два положения отрезка 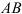
Первый вариант. Переместим фигуру поступательно, из положения 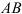
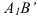
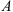
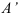
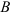
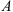
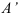
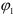
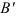
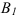
Второй вариант. Переместим фигуру поступательно из положения 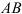
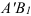
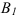
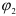
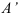
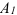
Как видно, поступательное перемещение плоской фигуры различно в различных вариантах, а величина угла поворота и направление поворота одинаковы, т. е.
Из этого следует, что
Плоскопараллельное движение можно рассматривать как совокупность двух движении: поступательного движения плоской фигуры вместе с произвольной точкой, называемой полюсом, и поворота вокруг полюса.
При этом поступательное перемещение зависит от выбора полюса, а величина угла поворота и направление поворота от выбора полюса не зависят.
Приняв за полюс некоторую точку 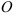
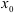
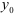
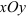
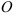
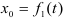
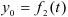
Вращательное движение фигуры относительно полюса можно описать уравнением
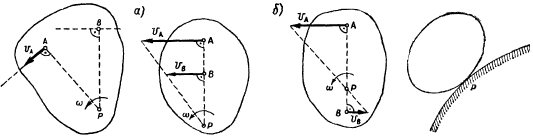
Определение скоростей точек плоском плоскопараллельное движение
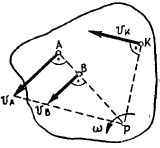
Скорость любой точки плоской фигуры равна геометрической сумме скорости полюса и вращательной скорости этой точки вокруг полюса.
Для плоской фигуры совершающей плоскопараллельное движение в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю. Эту точку называют мгновенным центром скоростей.
Способы определения мгновенного центра скоростей
Определение скоростей точек плоской фигуры при помощи мгновенного центра скоростей
Определим скорости точек 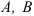
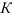
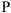
Если точка 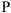
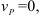
т. е. скорость любой точки плоской фигуры в данный момент времени представляет собой вращательную скорость этой точки вокруг мгновенного центра скоростей; поэтому
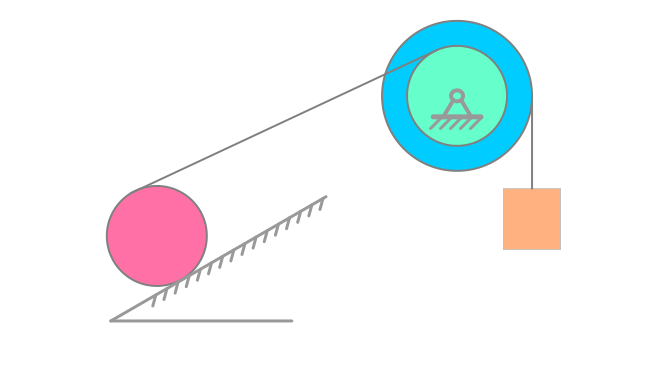
Пример:
Колесо радиусом 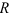
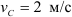
Определить скорости точек 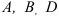
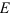
1-й вариант.
Примем за полюс центр колеса 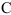
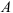
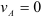
Точка 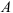
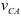
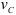
Расстояния от точек 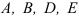
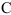
Откладывая в каждой точке скорость полюса 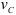
2-й вариант
Примем мгновенный центр скоростей колеса за полюс. Тогда скорости всех точек колеса определятся как вращательные скорости вокруг мгновенного центра скоростей.
Модули скоростей всех точек найдутся но пропорциональности скоростей их расстояниям от мгновенного центра скоростей: Найдем 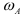
Обозначим радиус колеса через 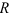
Возможно эта страница вам будет полезна:
Определение ускорений точек плоской фигуры совершающей плоскопараллельное движение
Ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении вокруг полюса.
Пример:
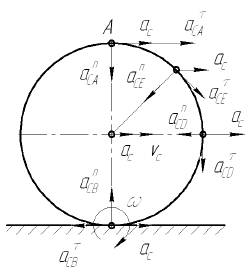
Колесо радиусом 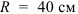
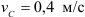
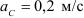
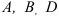
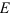
Определяем 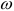
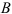
Определяем угловое ускорение.
Для точки 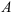
Для точки 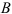
Для точки 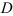
Для точки 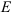
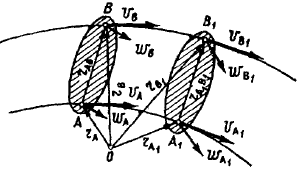
Разложение составного движении точки на относительное и переносное
Составное движение тонки (тела) — это такое движение, при котором точка (тело) одновременно участвует в двух или нескольких движениях.
Например, составное движение совершает лодка, переплывающая реку, пассажир, перемещающийся в вагоне движущегося поезда или по палубе плывущего парохода, а также человек, перемещающийся по лестнице движущегося эскалатора.
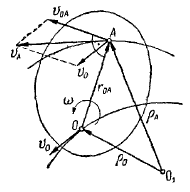
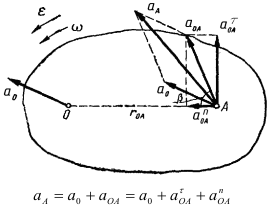
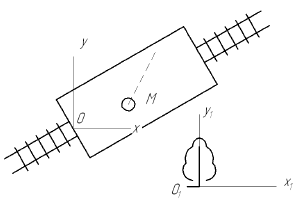
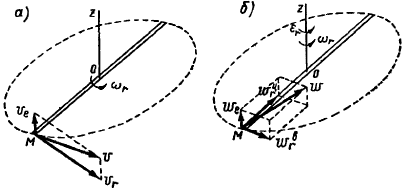
Через произвольную точку 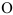
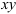
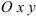
Неподвижной системой отсчета называют систему осей 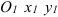
Движение точки 
Скорость и ускорение точки в абсолютном движении называют абсолютной скоростью и абсолютным ускорением точки и обозначают 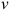
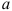
Движение точки 
Скорость и ускорение точки в относительном движении называют относительной скоростью и относительным ускорением точки и обозначают 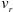
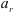
Движете подвижной системы отсчета 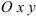
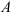
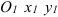

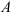
Скорость и ускорение точки тела 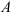

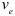
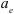
Движение точки 
Основная задача изучения составного движения состоит в установлении зависимостей между скоростями и ускорениями относительного, переносного и абсолютного движений точки.
Возможно эта страница вам будет полезна:
Определение скоростей и ускорений точки при составном движении
Теорема сложения скоростей
Абсолютная скорость точки равна геометрической сумме ее переносной и относительной скоростей.
Для нахождения абсолютной скорости необходимо:
Теорема сложения ускорении
В случае непоступательного переносного движения абсолютное ускорение точки равно геометрической сумме переносного, относительного и ускорения Кориолиса.
Поворотным ускорением (ускорением Кориолиса) называется составляющая абсолютного ускорения точки в составном движении, равная удвоенному векторному произведению угловой скорости переносного вращения на относительную скорость точки:
где 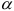
Направление ускорения Кориолиса находится но правилу: Относительную скорость точки следует спроектировать на плоскость, перпендикулярную оси переносного вращения, и повернуть эту проекцию в той же плоскости на 90°, в сторону переносного вращения.
Ускорение Кориолиса равно нулю в трех случаях:
Пример:
Вертикальный подъем вертолета происходит согласно уравнению 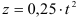
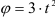
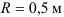
Свяжем подвижную систему отсчета с корпусом вертолета, неподвижную — с Землей. Относительное движение — вращение винта вокруг его оси является (это движение наблюдает пассажир вертолета, связанный с подвижной системой отсчета).
Переносное движение — является поступательное движение вертолета вертикально вверх.
Применяем теорему о сложении скоростей
Относительная скорость точки 
Если известен закон вращения винта 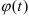
Вертолёт совершает поступательное движение. Переносная скорость точки 
Применяем теорему о сложении ускорений
Винт совершает вращательное движение. Следовательно относительное ускорение точки 
Переносная скорость точки 
Ускорение Кориолиса равно нулю так как Вертолёт совершает поступательное движение 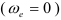
Так как 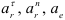
Пример:
Диск равномерно вращается с угловой скоростью 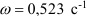
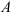
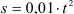
Определение положения точки
Определим, на какое расстояние переместится точка за время 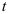
Определим, на какой угол повернется желоб за время
Если тело вращается равномерно, то за 1 сек тело повернется на 1 радиан (57,32°), тогда за 0,523 с тело повернется на 0,523 рад или 57,32 0,523 = 30°
Покажем на рисунке положение точки в момент времени t = 0,523 с.
Применяем теорему о сложении скоростей
Относительную скорость точки 
Переносная скорость точки 
Так как 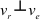
Применяем теорему о сложении ускорений
Относительное ускорение точки 
Переносное ускорение точки 
Так как тело движется с постоянной угловой скоростью 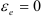
Возможно эта страница вам будет полезна:
Основы теории механизмов и машин (понятии и определении)
Классификации кинематических пар
Теория механизмов и машин — научная дисциплина (или раздел науки), которая изучает строение (структуру), кинематику и динамику механизмов.
Механизмом называется система твердых тел, предназначенная для передачи и преобразования заданного движения одного или нескольких тел в требуемые движения других твердых тел
Типовыми механизмами будем называть простые механизмы, имеющие при различном функциональном назначении широкое применение в машинах/
Звено — твердое тело или система жестко связанных гел. входящих в состав механизма.
Стойка — звено, которое при исследовании механизма принимается за неподвижное.
Входное звено — звено, которому сообщается заданное движение и соответствующие силовые факторы (силы или моменты);
Выходное звено — то, на котором получают требуемое движение и силы.
Кинематическая цепь — система звеньев, образующих между собой кинематические пары.
Кинематическая пара — подвижное соединение двух звеньев, допускающее их определенное относительное движение.
Элементами кинематической пары называют совокупность поверхностей, линий или точек, по которым происходит подвижное соединение двух звеньев и которые образуют кинематическую пару.
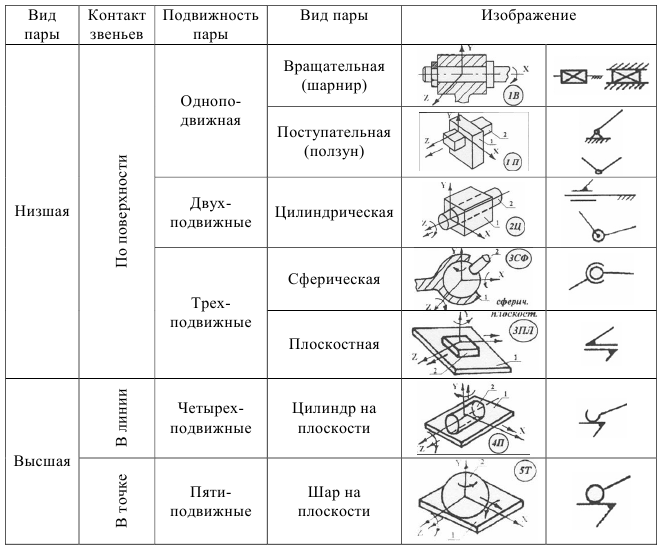
В зависимости от вида контакта элементов кинематических пар они делятся на высшие и низшие.
Кинематические пары, образованные элементами в виде линии или точки называются высшими.
Кинематические пары, образованные элементами в виде поверхностей, называются низшими.
В зависимости от степени подвижности они делятся на
Рычажные механизмы. Основные виды рычажных механизмов
Рычажным называется механизм, звенья которого образуют только вращательные и поступательные пары.
Составляющие рычажных механизмов.
Основные виды механизмов
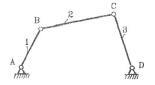
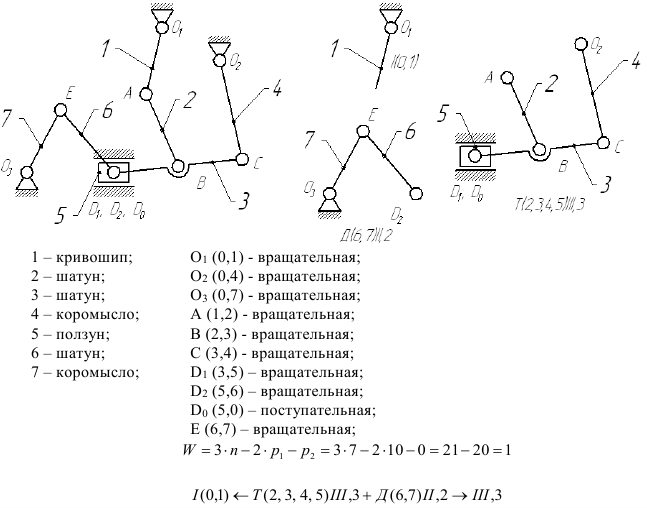
Кривошинно-шатунный механизм (Шарнирный чет ырехзвенник)
Состоит из кривошипа 1, шатуна 2, коромысла 3 и стойки, связанных между собой вращательными кинематическими парами
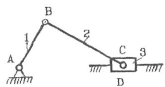
Состоит из кривошипа 1, шатуна 2, ползуна 3 и стойки, связанных между собой вращательными кинематическими парами 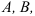
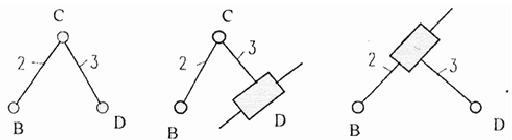
Состоит из кривошипа 1, кулисного камня 2, кулисы 3 и стойки, связанных между собой вращательными кинематическими парами 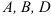
Структурный анализ механизмов
Структурный анализ механизма — это расчленение его на структурные группы. Структурные группы (группы Ассура) — это кинематические цепи, которые после присоединения к стойке имеют степень подвижности 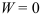
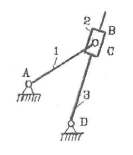
Степень подвижности механизма определяется по формуле Чебышева для рычажных механизмов.
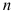
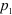
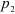
Структурную формулу любого простого или сложного механизма, образованного с помощью структурных групп, можно представить следующим образом:
За начальный механизм принимается ведущее звено со стойкой.
Все механизмы и структурные группы, в них входящие, делятся на классы, а класс-механизма в целом определяется высшим классом структурной группы, которая в него входит.
Элементарные механизмы условно отнесены к механизмам 1 класса.
Класс структурной группы определяется числом максимальным числом кинематических пар, на одном звене.
Порядок группы определяется числом внешних кинематических нар.
Виды структурных групп
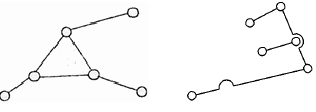
Диада — структурная группа II класса, 2 порядка (И, 2) Состоит из двух звеньев и трех кинематических пар.
Трехповодок (Триада) — структурная группа III класса, 3 порядка (III, 3) Состоит из четырех звеньев и шести кинематических пар.
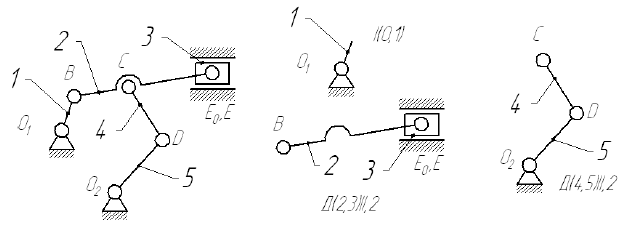
Порядок выполнения структурного анализа:
Пример:
Пример:
Возможно эта страница вам будет полезна:
Кулачковые механизмы
Кулачковые механизмы, подобно другим механизмам, служат для преобразования одного вида движения (на входе), в другой вид движения (на выходе) с одновременным преобразованием передаваемых силовых параметров (сил, моментов).
Основным преимуществом является возможность получения любого закона движения ведомого звена.
Кинематическая цепь простейшего кулачкового механизма состоит из двух подвижных звеньев (кулачка и толкателя), образующих высшую кинематическую пару, и стойки, с которой каждое из этих звеньев входит в низшую кинематическую пару.
Ведущим звеном механизма обычно является кулачок, который в большинстве случаев совершает непрерывное вращательное движение.
Ведомое звено, называемое толкателем, совершает возвратно-прямолинейное и возвратно-вращательное движение относительно стойки.
Классификация кулачковых механизмов
По виду выходного звена
По виду толкателя
По расположению толкателя
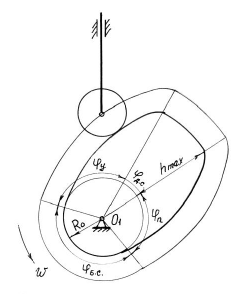
Основные параметры кулачка
Профиль кулачка — это профиль, образованный центром ролика обеспечивающий заданный закон движения ведомого звена.
Минимальный радиус кулачка 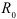
Максимальный радиус кулачка 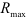
Максимальный подъем толкателя — расстояние между минимальным и максимальным радиусами кулачка 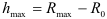
За один оборот кулачка происходит последовательное удаление толкателя от центра вращения кулачка, затем остановка и приближение к центру кулачка, вновь остановка и повторение всего цикла движения. Эти четыре этапа в движении кулачкового механизма называются фазами движения, которые ограничены соответствующими углами, называемыми фазовыми углами.
Фаза удаления 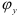
Фаза дальнего стояния 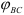
Фаза возврата 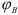
Фаза ближнего стояния 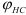
В некоторых кулачковых механизмах фазы ближнего и дальнего стояния могут отсутствовать, сразу обе или одна.
Рабочий угол кулачка — угол кулачка равный сумме углов удаления, дальнего стояния и возврата.
Угол давления — угол 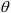
Зубчатые механизмы
Принцип действия и классификации. Основные параметры, геометрии и кинематика прямозубых колёс.
Принцип действия зубчатой передачи основан на зацеплении пары зубчатых колес.
Классификация:
По расположению осей валов:
По форме профиля зуба:
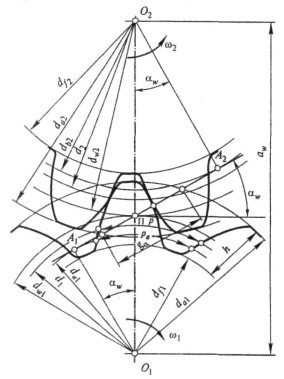
Основные параметры:
Ведущее зубчатое колесо называют шестерней, а ведомое — колесом. Параметрам шестерни приписывают индекс 1, а параметрам колеса — 2.
Геометрические параметры: 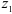
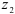
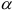
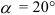
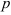
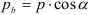
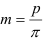
Модули стандартизованы (ГОСТ 9563-80) в диапазоне 0,05… 100 мм
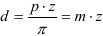
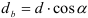
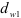
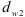
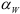
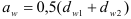
При нарезании колес со смещением делительная плоскость рейки смещается к центру или от центра заготовки на 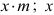
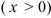
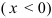
У передач без смещения и при суммарном смещении 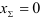
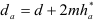
где 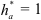
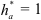
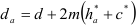
где 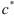
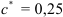
Передаточное отношение 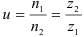
Виды зубчатых механизмов
Зубчатый механизм, составленный из зубчатых колес с неподвижными осями, называется зубчатым рядом.
Зубчатый ряд, состоящий из двух колес стойки, есть рядовая передача.
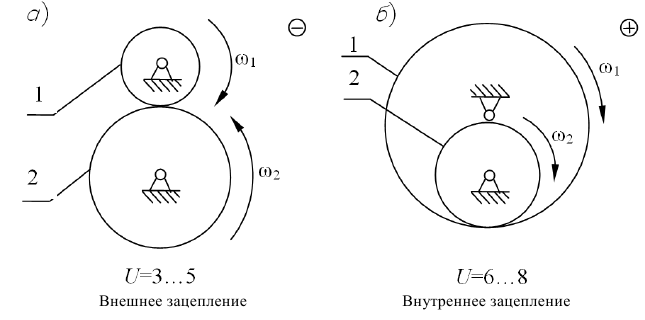
Значение передаточного отношения рядовой передачи обратно пропорционально числу зубьев колес:
Знак перед дробью позволяет учесть направление вращения колес. Для внешнего зацепления принят знак (-), учитывающий противоположность вращения колес. Для внутреннего зацепления принят знак (+).
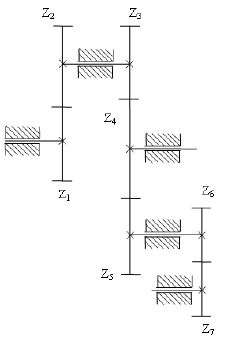
Передаточное отношение любого зубчатого ряда равно произведению передаточных отношений всех передач, входящих в него:
где 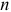
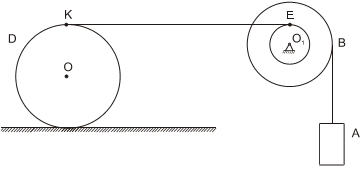
Определить передаточное отношение 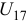
Общее передаточное отношение механизма равно:
Колесо 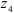
Зубчатый механизм, в состав которого входят зубчатые колеса с геометрически подвижной осью называются планетарным механизмом. В состав планетарного механизма входят звенья: Сателлиты — зубчатые колеса с геометрически подвижной осью;
Водило — подвижное звено, в котором помещена ось сателлита;
Солнечное колесо — подвижное центральное зубчатое колесо; Опорное колесо (эпицикл) — неподвижное центральное зубчатое колесо;
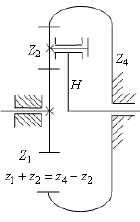
Геометрическая ось центральных колес и водила общая. Для обеспечения этого используют условие соосности
Определение передаточного отношении планетарной передачи
При исследовании кинематики планетарных передач широко используют метод остановки водила — метод Виллиса.
Всей планетарной передаче мысленно сообщается вращение с частотой вращения водила, но в обратном направлении. При этом водило, как бы затормаживается, а все другие звенья освобождаются. Получаем так называемый обращенный механизм, представляющий собой простую передачу, в которой движение передается от 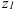
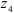
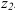
Для исследуемого механизма:
Для обращенного механизма:
В нашем случае 4 заторможено, 1 — ведущее и 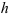
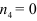
Основы материаловедения
Материалы, применяемые дли изготовления механизмов и машин.
Основным машиностроительным материалом является сплав железа и углерода, называемый чугуном или сталью в зависимости от процентного содержания углерода в сплаве.
Чугун содержит углерода свыше 2%. Различают:
Серый чугун (основной материал для литых деталей)
Маркировка: СЧ и цифры, соответствующие пределу прочности при растяжении (СЧ15- 150 МПа, СЧ20 — 200 МПа)
Свойства: жесткость, сравнительно малая прочность, хрупкость, хорошие литейные свойства,относительная дешевизна.
Высокопрочный чугун (чугун с повышенной прочностью).
Маркировка: ВЧ и цифры, соответствующие пределу прочности при растяжении (ВЧ40, ВЧ35)
Ковкий чугун (чугун с повышенным коэффициентом относительного удлинения)
Маркировка: КЧ 30-6, где 30 — предел прочности, 300 МПА; 6 — относительное удлинение, %.
Белый и отбеленный чугуны (не применяется).
Сталь — сплав железа с углеродом с содержанием углерода менее 1,6 %.
Сталь общего назначения (применяется для сварных соединений и в неответственных деталях)
Маркировка: ст 3, ст 5 (цифра обозначает условный номер марки в зависимости от химического состава)
Сталь качественная конструкционная (применяется для изготовления валов, стаканов, и.т.д.)
Маркировка: сталь 25, сталь 45 и т.п. Здесь цифры указывают содержание углерода в сотых долях процента.
Легированные стали (применяется для изготовления ответственных деталей зубчатых колес, червяков, цепей и.т.д) — это качественная конструкционная сталь с легирующими добавками, которые существенно улучшают свойства стали. В качестве легирующих добавок-чаще всего используют никель, хром, марганец и другие металлы.
Маркировка: сталь 40Х, сталь 40ХН, сталь 40 Х2Н. (здесь буквами X и Н обозначены хром и никель в количестве до 1%).
Сплавы на основе цветных металлов (применяются для изготовления венцов червячных колес, вкладышей подшипников скольжения и.т.д):
Сплав на основе меди:
Алюминиевые сплавы (используются для изготовления неответственных литых штампованных деталей ):
Маркировка: АЛ2, АЛ4 и т.п;
Основные механические характеристики материалов
Основные механические характеристики материала определяются при испытании образцов материала.
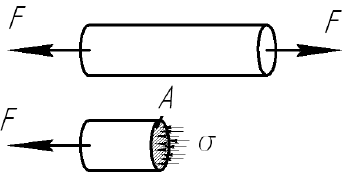
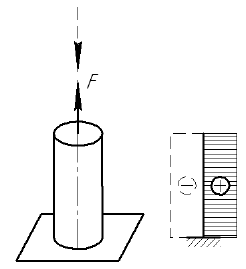
Рассмотрим цилиндр, находящийся под действием растягивающей силы 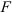
Под действием силы 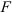
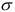
где 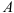
Постепенно будем увеличивать нагрузку 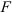
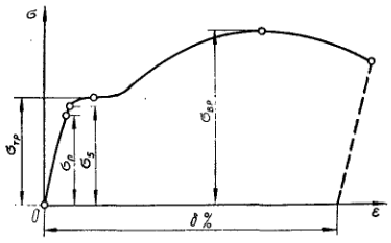
Для большинства материалов зависимость между напряжениями и деформациями выглядит следующим образом
Данная зависимость имеет следующие характерные точки:
Предел пропорциональности 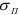
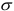
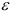
Предел упругости 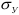
Предел текучести 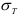
Предел прочности 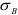
К основным характеристикам материалов также относятся:
Основы сопротивлении материалов
Геометрические характеристики сечений
Детали механизмов и машин отличаются друг от друга по форме и размерам. При расчета на прочность деталей механизмов и машин используются поперечные сечения деталей, имеющие свои геометричекие характеристики.
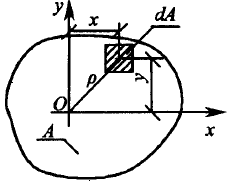
Рассмотрим геометричекие характеристики плоских сечений.
Площадь —
Статический момент относительно оси 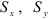
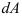
где 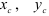
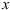
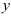
Статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси:
где 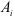
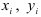
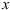
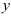
Последнее выражение позволяет определить положение центра тяжести для любого составного сечения
Пример:
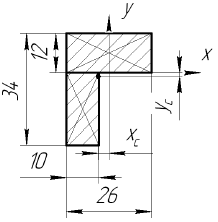
Определить положение центра тяжести сечения показанного на рисунке.
Проводим оси 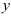
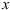
Находим расстояние от центров тяжестей фигур до осей
Записываем выражение для статических моментов инерции
Осевой момент инерции относительно оси сумма произведений площадей элементарных площадок 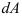
Полярный момент инерции плоского сечения относительно некоторой точки (полюса) 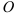
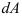
Пример:
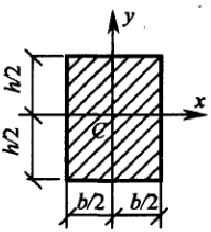
Определить осевые и полярный моменты инерции прямоугольника высотой 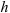
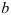
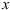
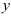
Представим 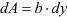
Представим 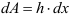
Осевой момент сопротивления относительно оси — отношение осевого момента инерции к расстоянию от наиболее удаленной точки сечения по этой оси
Полярный момент сопротивления относительно точки (полюса) — отношение полярного момента инерции к расстоянию от наиболее удаленной точки сечения до полюса
Пример:
Для предыдущего примера определить осевые и полярные моменты сопротивления
Для основных сечений формулы для расчета геометрических характеристик приводятся в технических справочниках.
Виды нагружения
Растяжение-сжатие
При воздействии на тело силы, линия действия которой проходит по оси данного тела, в поперечном сечении (перпендикулярном линии действия силы) возникают напряжения, называемые напряжениями растяжения или сжатия, в зависимости от направления действия силы.
В случае растяжения-сжатия прочность тела оценивается но формуле
где 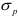
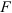
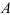
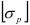
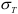
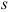
Для удобства представления информации на расчетной схеме напряжения представляются в виде эпюр.
Эпюра — группа условных линий, показывающих величину и направление напряжений, возникающих в рассматриваемом теле.
Если по длине тела изменяются размеры поперечного сечения или приложенная нагрузка, то изменятся и величина напряжений
Пример:
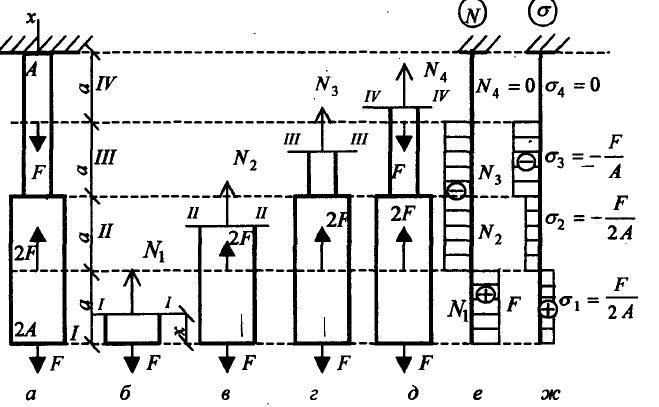
Построить эпюры напряжений для бруса, изображенного на рисунке.
Решение. Для определения внутренних усилий разбиваем прямолинейный брус на участки. Границами участков являются точки продольной оси, соответствующие изменению площади поперечного сечения и точкам приложения сосредоточенных сил.
Проводим сечение I-I. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой 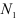
Определим напряжения на участке I:
Проводим сечение II—II. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой 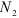
Определим напряжения на участке II:
Проводим сечение III—III. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой 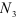
Определим напряжения на участке III:
Проводим сечение IV-IV. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой 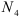
Определим напряжения на участке IV:
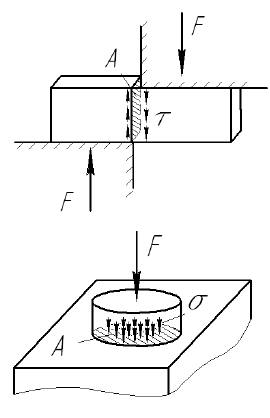
Срез (сдвиг) и смятие
Срезом называют деформацию, представляющую собой смещение поперечных плоскостей тела под действием силы параллельной этой плоскости.
Касательные напряжения при срезе (напряжения среза) определяются по формуле
где 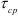
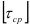
Смятием называют деформацию, представляющую собой нарушение первоначальной формы поверхности под действием силы перпендикулярной к этой поверхности.
Нормальные напряжения при смятии (напряжения смятия) определяются по формуле
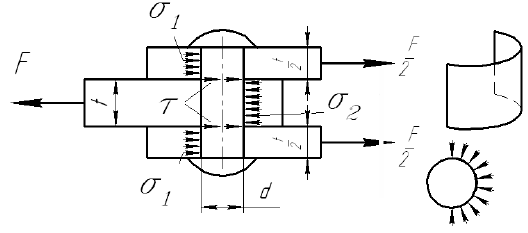
Определить напряжения среза и смятия для заклепки соединяющей три детали. Известны диаметр заклепки 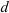
Запишем условие прочности на срез для заклепки
В соединении 3-х деталей напряжения среза возникают в двух сечениях круглой формы.
Площадь круга 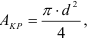
Запишем условие прочности на смятие для заклепки
В соединении 3-х деталей напряжения смятия возникают на боковых поверхностях заклепки площадь которых будет определяться:
Для верхней и нижней поверхностей:
Для средней поверхности:
Тогда напряжения смятия
Для верхней и нижней поверхностей:
Для средней поверхности:
Возможно эта страница вам будет полезна:
Изгиб
Изгиб представляет собой такую деформацию, при которой происходит искривление оси прямого бруса или изменение кривизны кривого бруса.
Изгиб называют чистым если изгибающий момент является единственным внутренним усилием, возникающим в поперечном сечении бруса (балки).
Изгиб называют поперечным, если в поперечных сечениях бруса наряду с изгибающими моментами возникают также и поперечные силы.
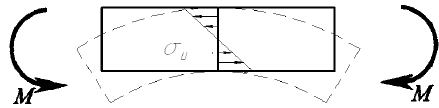
При изгибе в сечении деталей возникают нормальные напряжения 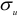
Напряжения изгиба определяются по формуле
На практике изгиб тела вызывает не только внешние изгибающие моменты, но и поперечные силы, действующие на тело. Для нахождения наиболее нагруженного поперечного сечения строят эпюры изгибающих моментов.
При построении эпюр изгибающих моментов используются следующие правила:
Построение эпюр изгибающих моментов рассмотрим на примере.
Пример:
Проверить на прочность балку постоянного сечения, показанную на рисунке, если известно, что осевой момент сопротивления ее сечения