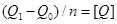Что не относится к свойствам величины
Физические свойства, величины и шкалы
ВАЖНО!
В связи с происходящим в настоящее время пересмотром Правительством и Государственной думой РФ законодательства о техническом регулировании, введением новых видов нормативных документов и изменением уже существующих некоторые положения данного учебного пособия могут устареть за время подготовки издания к выходу в свет.
Глава 1. МЕТРОЛОГИЯ
Метрология – это наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
В зависимости от цели различают три раздела метрологии: теоретический, законодательный и прикладной.
В теоретической (фундаментальной) метрологии разрабатываются фундаментальные основы этой науки.
Предметом законодательной метрологии является установление обязательных технических и юридических требований по применению единиц физических величин, эталонов, методов и средств измерений, направленных на обеспечение единства и необходимой точности измерений.
Практическая (прикладная) метрология освещает вопросы практического применения разработок теоретической и положений законодательной метрологии.
Все объекты окружающего мира характеризуются своими свойствами. Свойство – философская категория, выражающая такую сторону объекта (явления процесса), которая обусловливает его различие или общность с другими объектами (явлениями, процессами) и обнаруживается в его отношениях к ним. Свойство – категория качественная. Для количественного описания различных свойств процессов и физических тел вводится понятие величины. Величина – это свойство чего-либо, что может быть выделено среди других свойств и оценено тем или иным способом, в том числе и количественно. Величина не существует сама по себе, она имеет место лишь постольку, поскольку существует объект со свойствами, выраженными данной величиной.
Величины можно разделить на два вида: реальные и идеальные (рис. 1.1).
Рис. 1.1. Классификация величин
Идеальные величины главным образом относятся к математике и являются обобщением (моделью) конкретных реальных понятий.
Реальные величины делятся, в свою очередь, на физическиеи нефизические. Физическая величина (ФВ) в общем случае может быть определена как величина, свойственная материальным объектам (процессам, явлениям), изучаемым в естественных (физика, химия) и технических науках. К нефизическим следует отнести величины, присущие общественным (нефизическим) наукам, – философии, социологии, экономике и т.д.
Рекомендации РМГ 29-99 трактуют физическую величину как одно из свойств физического объекта, в качественном отношении общее для многих физических объектов,
а в количественном – индивидуальное для каждого из них. Индивидуальность в количественном отношении понимают в том смысле, что свойство может быть для одного объекта в определенное число раз больше или меньше, чем для другого. Таким образом, физические величины – это измеренные свойства физических объектов и процессов, с помощью которых они могут быть изучены.
Физические величины целесообразно разделить на измеряемые и оцениваемые. Измеряемые ФВ могут быть выражены количественно в виде определенного числа установленных единиц измерения.
Возможность введения и использования последних является важным отличительным признаком измеряемых ФВ. Физические величины, для которых по тем или иным причинам не может быть введена единица измерения, могут быть только оценены. Величины оценивают при помощи шкал. Шкала величины – упорядоченная последовательность ее значений, принятая по соглашению на основании результатов точных измерений.
Нефизические величины, для которых единица измерения в принципе не может быть введена, могут быть только оценены. Стоит отметить, что оценивание нефизических величин не входит в задачи теоретической метрологии.
Для более детального изучения ФВ необходимо классифицировать (рис. 1.2) и выявить общие метрологические особенности их отдельных групп.
По видам явлений ФВ делятся на следующие группы:
¨ вещественные, т.е. описывающие физические и физико-химические свойства веществ, материалов и изделий из них. К этой группе относятся масса, плотность, электрическое сопротивление, емкость, индуктивность и др. Иногда указанные ФВ называют пассивными. Для их измерения
необходимо использовать вспомогательный источник энергии, с помощью которого формируется сигнал измерительной информации. При этом пассивные ФВ преобразуются в активные, которые и измеряются;
¨ энергетические, т.е. величины, описывающие энергетические характеристики процессов преобразования, передачи и использования энергии. К ним относятся ток, напряжение, мощность, энергия. Эти величины называют активными. Они могут быть преобразованы в сигналы измерительной информации без использования вспомогательных источников энергии;
¨ характеризующие протекание процессов во времени. К этой группе относятся различного рода спектральные характеристики, корреляционные функции и другие.
По принадлежности к различным группам физических процессов ФВ делятся на пространственно-временные, механические, тепловые, электрические и магнитные, акустические, световые, физико-химические, ионизирующих излучений, атомной и ядерной физики.
По степени условной независимости от других величин данной группы ФВ делятся на основные (условно независимые), производные (условно зависимые) и дополнительные. В настоящее время в международной системе единиц (СИ) используются семь физических величин, выбранных в качестве основных: длина, время, масса, температура, сила электрического тока, сила света и количество вещества. К дополнительным физическим величинам относятся плоский и телесный углы.
По наличию размерности ФВ делятся на размерные, т.е. имеющие размерность, и безразмерные.
Совокупность чисел Q, отображающая различные по размеру однородные величины, должна быть совокупностью одинаково именованных чисел. Это именование является единицей ФВ или ее доли. Единица физической величины [Q] – это ФВ фиксированного размера, которой условно присвоено числовое значение, равное единице, применяется для количественного выражения однородных ФВ.
Значение физической величины Q – это оценка ее размера в виде некоторого числа принятых для нее единиц.
Числовое значение физической величины q – отвлеченное число, выражающее отношение значения величины к соответствующей единице данной ФВ.
называют основным уравнением измерения. Суть простейшего измерения состоит в сравнении ФВ Q c размерами выходной величины регулируемой многозначной меры a[Q]. В результате сравнения устанавливают, что q[Q]
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Физические свойства и величины



Все объекты окружающего мира характеризуются своими свойствами. В общем случае свойств, которыми обладает данный объект или явление – бесчисленное множество. Но благодаря этим свойствам, мы можем отличить один объект от другого или, наоборот, сгруппировать их, т. е. отнести к какому-то одному классу объектов. Например, большой, теплый, тяжелый. Свойство объекта проявляется только в его взаимодействии с другими объектами. Например, свойство упругости мяча проявляется при его взаимодействии с полом.
Свойство – философская категория, выражающая такую сторону объекта (явление процесса), которая обусловливает его различность или общность с другими объектами (явлениями, процессами) и обнаруживается в его отношениях к ним. Свойство – категория качественная. Для количественного описания различных свойств процессов и физических тел вводится понятие величины.
Величина – это свойство чего-либо, что может быть выделено среди других свойств и оценено тем или иным способом, в том числе и количественно. Величина не существует сама по себе, она имеет место лишь постольку, поскольку существует объект со свойствами, выраженными данной величиной.
Величины можно разделить на два вида: реальные и идеальные.
Идеальные величины главным образом относятся к математике и являются обобщением (моделью) конкретных реальных понятий.
Реальные величины делятся, в свою очередь, нафизические и нефизические. Физическая величина (ФВ) в общем случае может быть определена как величина, свойственная материальным объектам (процессам, явлениям), изучаемым в естественных (физика, химия) и технических науках. К нефизическим следует отнести величины, принадлежащие общественным (нефизическим) наукам – философии, социологии, экономике и т. д.
Физическая величина – одно из свойств физического объекта, в качественном отношении общее для многих физических объектов, а в количественном – индивидуальное для каждого из них. Индивидуальность в количественном отношении понимают в том смысле, что свойство может быть для одного объекта в определенное число раз больше или меньше, чем для другого. Например, физические объекты обладают массой – это их общее свойство. Но каждое тело имеет в количественном отношении свое значение массы. Таким образом, физические величины – это измеренные свойства физических объектов и процессов, с помощью которых они могут быть изучены.
Физические величины целесообразно разделить на измеряемые и оцениваемые. Измеряемые ФВ могут быть выражены количественно в виде определенного числа установленных единиц измерения. Возможность введения и использования последних является важным отличительным признаком измеряемых ФВ. Физические величины, для которых по тем или иным причинам не может быть введена единица измерения, могут быть только оценены. Величины оценивают при помощи шкал.
Шкала величины – упорядоченная последовательность ее значений, принятая по соглашению на основании результатов точных измерений.
Нефизические величины, для которых единица измерения в принципе не может быть введена, могут быть только оценены. Оценивание нефизических величин не входит в задачи теоретической метрологии.
Единица физической величины [Q] – это ФВ фиксированного размера, которой условно присвоено числовое значение, равное единице, применяется для количественного выражения однородных ФВ.
Значение физической величины Q – это оценка ее размера в виде некоторого числа принятых для нее единиц.
Числовое значение физической величины q – отвлеченное число, выражающее отношение значения величины к соответствующей единице данной ФВ.
называют основным уравнением измерения.
Измерение – познавательный процесс, заключающийся в сравнении путем физического эксперимента данной ФВ с известной ФВ, принятой за единицу измерения.
В практической деятельности необходимо проводить измерения различных величин, характеризующих свойства тел, веществ, явлений и процессов. Некоторые свойства проявления (количественные или качественные) любого свойства образуют множества, отображения элементов которых на упорядоченное множество чисел или в более общем случае условных знаков образуют шкалы измерения этих свойств. Шкала измерений количественного свойства является шкалой ФВ.
Шкала физической величины – это упорядоченная последовательность значений ФВ, принятая по соглашению на основании результатов точных измерений.
Различают пять основных типов шкал измерений.
1. Шкала наименований (шкала классификации). Шкалы такого вида не являются шкалами ФВ. Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен. В этих шкалах отнесение отражаемого свойства к тому или иному классу эквивалентности осуществляется с помощью органов чувств человека – это наиболее адекватный результат, выбранный большинством экспертов. Нумерация объектов по шкале наименований осуществляется по принципу: “не приписывай одну и ту же цифру разным объектам”. В этих шкалах отсутствуют понятия нуля, “больше” или “меньше” и единицы измерения. Примером шкал наименований являются широко распространенные атласы цветов, предназначенные для идентификации цвета.
2. Шкала порядка (шкала рангов). В шкалах порядка существует или не существует нуль, но принципиально нельзя ввести единицы измерения. Эти шкалы являются монотонно возрастающими или убывающими, что позволяет установить отношение больше/меньше между величинами. К таким шкалам, например, относится шкала Мооса для определения твердости минералов, которая содержит 10 опорных (реперных) минералов с различными условными числами твердости: тальк – 1; гипс – 2; кальций – 3; флюорит – 4; апатит – 5; ортоклаз – 6; кварц – 7; топаз – 8; корунд – 9; алмаз – 10. Отнесение минерала к той или иной градации твердости осуществляется на основании эксперимента, который состоит в том, что испытуемый материал царапается опорным. Если после царапанья испытуемого минерала кварцем (7) на нем остается след, а после ортоклаза (6) не остается, то твердость испытуемого материала составляет более 6, но менее 7. Более точного ответа в этом случае дать невозможно. В условных шкалах одинаковым интервалам между размерами данной величины не соответствуют одинаковые размерности чисел, отображающих размеры. Определение значения величин при помощи шкал порядка нельзя считать измерением, так как на этих шкалах не могут быть введены единицы измерения. Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным.
3. Шкала интервалов (шкала разностей). Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. К таким шкалам относится летоисчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо Рождество Христово и т. д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.
Шкала интервалов величины Q можно представить в виде уравнения:
где q – числовое значение величины; Q0 – начало отсчета шкалы; [Q] – единица рассматриваемой величины.
Такая шкала полностью определяется значением начала отсчета Q0 шкалы и единицы данной величины [Q]. Задать шкалу можно двумя путями. При первом пути выбираются два значения Q0 и Q1 величины, которые относительно просто реализованы физически. Эти значения называются опорными точками, или основными реперами, а интервал (Q1-Q0) – основным интервалом. Точка Q0 принимается за начало отсчета, а величина:
за единицу измерения.
4. Шкала отношений. Их примерами являются шкала массы, термодинамической температуры. В шкалах отношений существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений. Шкалы отношений – самые совершенные. Они описываются уравнением:
где Q – ФВ, для которой строится шкала; [Q] – ее единица измерения; q – числовое значение ФВ.
5. Абсолютные шкалы. Под абсолютными понимают шкалы, обладающие всеми признаками шкал отношений, но дополнительно имеющие естественное однозначное определение единицы измерения и не зависящие от принятой системы единиц измерения. Такие шкалы соответствуют относительным величинам: коэффициенту усиления, ослабления и др.
Шкалы наименований и порядка называют неметрическими (концептуальными), а шкалы интервалов и отношений – метрическими (материальными).
Лекция Свойство. Величина. Основное уравнение измерения. Измерения.
Лекция 1.Свойство. Величина. Основное уравнение измерения
Основное содержание курса «Геодезические приборы и измерения» составляют средства измерений величин, являющихся для геодезии основными. Поэтому естественным представляется желание прояснить вопрос, что такое величина, что такое измерение, что такое средство измерения.
Детально величины, измерения и средства измерений изучаются в курсе «Метрология», который будет вам читаться на четвертом курсе. Здесь же мы рассмотрим основные моменты, знание которых потребуется нам в курсе «Геодезические приборы и измерения».
1. Свойство. Величина. Основное уравнение измерения
Все объекты окружающего мира характеризуются своими свойствами.
Свойство – это философская категория, выражающая такую сторону объекта (явления или процесса), которая обусловливает его различие или общность с другими объектами (явлениями, процессами) и обнаруживается в его отношениях к ним.
Свойство – категория качественная.
Например, можно назвать такие свойства предметов, как цвет, вес, длина, высота, плотность, твердость, мягкость и т.д. Однако из того факта, что некоторый предмет цветной или длинный, мы ничего, кроме того, что у него есть свойство цвета или протяженности, не узнаем.
Для количественного же описания различных свойств, процессов и физических тел вводится понятие величины.
Величина – это свойство чего-либо, что может быть выделено среди других свойств и оценено тем или иным способом, в том числе и количественно. Величина не существует сама по себе, она имеет место лишь постольку, поскольку существует объект со свойствами, выраженными данной величиной.
Рис. 3.1 – Классификация величин
Идеальные величины относятся главным образом к математике и являются обобщением (моделью) конкретных реальных понятий. Нас они не интересуют.
К нефизическим следует отнести величины, присущие общественным (нефизическим) наукам – философии, социологии, экономике и т.д. Эти величины нас не интересуют.
Физическая величина в общем случае может быть определена как величина, свойственная материальным объектам (процессам, явлениям), изучаемым в естественных (физика, химия) и технических науках. Именно эти величины и представляют для нас интерес.
Физическая величина в общем случае понимается как одно из свойств физического объекта, в качественном отношении общее для многих физических объектов, а в количественном отношении – индивидуальное для каждого из них.
Индивидуальность в количественном отношении понимают в том смысле, что свойство может быть для одного объекта в определенное число раз больше или меньше, чем для другого.
Например, каждый предмет на Земле обладает таким свойством как вес. Если взять несколько яблок, то каждое из них обладает весом. Но, в то же время, вес каждого яблока будет отличаться от веса других яблок.
Физические величины можно разделить на измеряемые и оцениваемые.
Измеряемые физические величины могут быть выражены количественно в виде определенного числа установленных единиц измерения. Возможность введения и использования единиц измерения является важным отличительным признаком измеряемых физических величин.
Физические величины, для которых по тем или иным причинам не может быть выполнено измерение или не может быть введена единица измерения, могут быть только оценены. Такие физические величины называются оцениваемыми. Оценку таких физических величин производят при помощи условных шкал. Например, интенсивность землетрясений оценивается по шкале Рихтера, твёрдость минералов – по шкале Мооса.
С помощью основных семи и двух дополнительных величин, введенных исключительно для удобства, образуется все многообразие производных физических величин и обеспечивается описание свойств физических объектов и явлений.
Размерность измеряемой величины является качественной ее характеристикой и обозначается символом 

Размерность производной физической величины выражается через размерности основных физических величин с помощью степенного одночлена:

где 





При этом каждый из показателей размерности может быть положительным или отрицательным, целым или дробным числом, а также нулем.
Если все показатели размерности равны нулю, то такая величина называется безразмерной.
Размер измеряемой величины является количественной ее характеристикой.
Получение информации о размере физической величины
является содержанием любого измерения.
Например, длина доски это количественная характеристика доски. Сама же длина может быть определена только в результате измерения.
Совокупность чисел, отображающая различные по размеру однородные величины, должна быть совокупностью одинаково именованных чисел. Это именование является единицей физической величины или ее доли. Тот же пример с длиной доски. Имеется совокупность чисел, характеризующих длину различных досок: 110, 115, 112, 120, 117. Все числа именуются сантиметрами. Именование сантиметр является единицей физической величины, в данном случае единицей длины.
Единица физической величины 
Например, метр, килограмм, секунда.
Значение физической величины 
. Например, 54.3 метра, 76.8 килограмм, 516 секунд.
Само же числовое значение физической величины 
Например, 54.3, 76.8, 516.
Все три перечисленных параметра связаны между собой соотношением
Из основного уравнения измерения следует, что измерение – это определение значения величины или, иначе, это сопоставление величины с ее единицей. Измерения физических величин производится с помощью технических средств. Можно дать следующее определение измерению.
Измерение – это совокупность операций для определения отношения одной (измеряемой) физической величины к другой однородной величине, принятой за единицу, хранящуюся в техническом средстве (средстве измерений).
Получившееся значение называется числовым значением измеряемой физической величины. Числовое значение совместно с обозначением используемой единицы называется значением физической величины.
Данное определение содержит четыре признака понятия измерение.
1. Измерять можно только физические величины (т.е. свойства материальных объектов, явлений, процессов).
2. Измерение – это оценивание величины опытным путем, т.е. это всегда эксперимент.
Нельзя назвать измерением расчетное определение величины по формулам и известным исходным данным.
3. Измерение осуществляется с помощью специальных технических средств – носителей размеров единиц или шкал, называемых средствами измерений.
4. Измерение – это определение значения величины, т.е. это сопоставление величины с ее единицей или шкалой. Такой подход выработан многовековой практикой измерений. Он вполне соответствует содержанию понятия «измерение», которой дал более 200 лет назад Л.Эйлер: « Невозможно определить или измерить одну величину иначе, как приняв в качестве известной другую величину этого же рода и указав соотношение, в котором она находится к ней » .
Измерение физической величины включает в себя два (вообще, может быть и несколько) этапа:
а) сравнение измеряемой величины с единицей;
б) преобразование в форму, удобную для использования (различные способы индикации).
В измерениях различают:
а) принцип измерений – это физическое явление или эффект, положенные в основу измерений;
б) метод измерений – прием или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализованным принципом измерений. Метод измерений обычно обусловлен устройством средств измерений.
Все возможные измерения, встречающиеся в практике человека, можно классифицировать по нескольким направлениям.
1. Классификация по видам измерений:
а) прямое измерение – измерение, при котором искомое значение физической величины получают непосредственно.
Примеры: измерение длины линии мерной лентой, измерение горизонтального или вертикального углов теодолитом;
б) косвенное измерение – определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.
Пример 1. Измерение длин линий параллактическим способом, при котором измеряется горизонтальный угол на марки базисной рейки, расстояние между которыми известно; искомая длина вычисляется по формулам, связывающим эту длину с горизонтальным углом и базисом.
Пример 2. Измерение длины линии светодальномером. В этом случае непосредственно измеряется не сама длина линии, а время прохождения электромагнитного импульса между излучателем и отражателем, установленными над точками, между которыми измеряется длина линии.
Пример 3. Определение пространственных координат точки земной поверхности с использованием Глобальной Навигационной Спутниковой Системы (ГНСС). В этом случае измеряются не координаты и даже не длины, а опять-таки время прохождения сигнала от каждого спутника до приемника. По измеренному времени косвенным образом определяются расстояния от спутников до приемника, а затем уже, опять-таки, косвенным способом, – координаты точки стояния.
в) совместные измерения – проводимые одновременно измерения двух или нескольких неодноименных величин для определения зависимости между ними.
Пример. Измерение длины металлического стержня и температуры, при которой измеряется длина стержня. Результатом таких измерений является определение коэффициента линейного расширения металла, из которого выполнен стержень, из-за изменения температуры.
г) совокупные измерения – проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.
2. Классификация по методам измерений:
а) метод непосредственной оценки – метод, при котором значение величины определяют непосредственно по показывающему средству измерений;
примеры измерение давления по барометру или температуры по термометру;
б) метод сравнения с мерой – метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой;
прикладывая линейку с делениями к какой-либо детали, по сути сравнивают ее размер с единицей, хранимой линейкой, и, произведя отсчет, получают значение величины (длины, высоты, толщины и других параметров);
с помощью измерительного прибора сравнивают размер величины (например, угла), преобразованной в перемещение указателя (алидады), с единицей, хранимой шкалой этого прибора (горизонтальным кругом, деление круга – это мера), и проводят отсчет.
Характеристикой точности измерения является его погрешность или неопределенность.
При производстве измерений реальный объект измерения всегда заменяют его моделью, которая вследствие своего несовершенства отличается от реального объекта. Вследствие этого величины, характеризующие реальный объект также будут отличаться от аналогичных величин этого же объекта. Это приводит к неизбежным погрешностям измерений, которые в общем случае подразделяются на случайные и систематические.
Метод измерений. Выбор метода измерений определяется принятой моделью объекта измерения и доступными средствами измерений. При выборе метода измерений добиваются того, чтобы погрешность метода измерений, т.е. составляющая систематической погрешности измерений, обусловленная несовершенством принятых модели и метода измерений (иначе теоретическая погрешность), не сказывалась заметно на результирующей погрешности измерения, т.е. не превышала 30% от нее.
Модель объекта. Изменения измеряемых параметров модели в течение цикла наблюдений, как правило, не должны превышать 10% от заданной погрешности измерения. Если возможны альтернативы, то учитывают и экономические соображения: ненужное завышение точности модели и метода измерения приводят к необоснованным затратам. То же относится и к выбору средств измерений.
Средства измерений. Выбор средств измерений и вспомогательных устройств определяется измеряемой величиной, принятым методом измерений и требуемой точностью результатов измерений (нормами точности). Измерения с применением средств измерений недостаточной точности малоценны (даже бессмысленны), так как могут быть причиной неправильных выводов. Применение излишне точных средств измерений экономически невыгодно. Учитывают также диапазон изменений измеряемой величины, условия измерений, эксплуатационные качества средств измерений, их стоимость.
Основное внимание уделяют погрешностям средств измерений. Необходимо чтобы суммарная погрешность результата измерения 


где