Что не относится к основным характеристикам колебательного движения

Лекция по физике на тему «Колебательное движение. Гармонические колебания.»

Колебательное движение. Гармонические колебания.

Наряду с поступательными и вращательными движениями тел в механике значительный интерес представляют и колебательные движения.

Колебаниями называется процессы, отличающиеся той или иной степенью повторяемости (качели, ветка дерева, фазы луны, морские приливы и отливы, пульсовая волна, сердце, гортань…).

В технике и окружающем нас мире часто приходится сталкиваться с периодическими (или почти периодическими) процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.

Колебания широко распространены в природе и технике. Колебательные процессы лежат в основе таких отраслей техники как электротехника, радиотехника и.т.д).

Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Примерами простых колебательных систем могут служить груз на пружине или математический маятник.

Математический маятник – подвешенный на тонкой невесомой нити груз, размерами которого можно пренебречь по сравнению с размерами нити. В процессе колебания маятника происходит изменения координаты, скорости.

Период колебания математического маятника:

Т- период колебаний

g – ускорение свободного падения

Гюйгенс доказал, что период малых колебаний маятника не зависят от времени. Используя это свойство, названное изохронностью маятника Гюйгенс в тысяча шестьсот пятьдесят седьмом году, сконструировал первые маятниковые часы. Это свойство маятника было открыто 19-летним Галилеем более чем за 20 лет до открытия Гюйгенса. Наблюдая за тем, как раскачиваются в соборе светильники, подвешенные на нитях одинаковой длины, он заметил, что их период колебаний не зависит от времени. Наручных часов тогда не было, и юный Галилей пришёл к решению, которое для многих поколений будет служить образцом блеска и остроумия человеческой мысли: он сравнил колебания маятника с частотой биения собственного сердца.

Пружинный маятник – невесомая пружина, к которой прикреплено тело массой m .

Период колебания пружинного маятника

κ – жесткость пружины [Н/м]

Условия возникновения колебаний:

1. Вывести тело из положения равновесия.

2. Уменьшить силу трения.

В зависимости от характера воздействия на колеблющуюся систему, различают: свободные (собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания.

Самым простым колебательным движением тела является гармоническое колебание. Гармоническим называют колебание, в процессе которого величины, характеризующие движение (смещение, скорость, ускорение и др.), изменяются по закону синуса или косинуса (гармоническому закону). В общем виде этот закон задается формулой:

где x ( t ) — значение изменяющейся величины в момент времени t (смещение или отклонение), A — амплитуда колебаний (максимальное смещение), ω — циклическая (круговая) частота колебаний, j ₀ — начальная фаза колебаний.

Этот вид колебаний важен по двум причинам:

колебания в природе и технике часто близки к гармоническому.

иные периодические процессы могут быть представлены как наложение нескольких гармонических колебаний.

Частота колебаний n – число полных колебаний за единицу времени [υ] = Гц (Герц)

n = ; n = ; Т=

Период колебаний – минимальный промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебание [ T ]=с

Т=

Одно полное колебание равно 4 амплетудам.

Циклическая (круговая) частота – число полных колебаний, которые совершаются за 2π единиц времени ( ω – омега [рад/с]). w ₀ = 2 pn

w =

Частота и период гармонических колебаний не зависят от амплитуды.

Фаза колебания ( ωt + j ₀ ) – это величина, стоящая под знаком синуса или косинуса [рад].

Фаза колебания в начальный момент времени ( t =0) называется начальной фазой j ₀ [рад].

Резонанс – резкое возрастание амплитуды вынужденных колебаний.

Резонанс возникает только в том случае, когда частота собственных колебаний совпадает с частотой вынужденных сил.

Впервые явление резонанса было описано Галилеем. Явление резонанса играет большую роль в природе, технике и науке. Большинство сооружений и машин обладая определенной упругостью, способно совершать свободные колебания. Поэтому внешние периодические воздействия могут вызвать их резонанс, что может стать причиной катастроф. Известно много случаев, когда источником опасных колебаний были люди, идущие в ногу. Так, в 1831 году в городе Манчестер при прохождении по мосту колонны солдат строевым шагом мост разрушился. Аналогичный случай был в г. Петербурге в 1905 году. При прохождении моста через реку Фонтанка эскадроном гвардейской кавалерии мост обрушился. Для предотвращения резонансных явлений используют разные способы гашения вынужденных колебаний. Один способ состоит в изменении частоты свободных колебаний в системе. Другой способ состоит в увеличении силы трения в системе: чем больше сила трения, тем меньше амплитуда резонансных колебаний

Затухающие колебания – это колебания, которые под действием сил трения или сопротивления, со временем уменьшается.

Незатухающие колебания – это колебания, которые со временем не изменяются; силы трения и сопротивления отсутствуют. Для поддержания незатухающих колебаний необходим источник энергии.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник

Частная школа. 9 класс

Конспекты, контрольные, тесты

Характеристики колебательного движения

Конспект по физике для 9 класса «Маятник. Характеристики колебательного движения». Что такое математический маятник. Что такое период и частота колебаний. Что такое амплитуда колебаний. Как выглядит график колебательного движения.

Маятник. Характеристики
колебательного движения

Линейка, висящая на гвоздике, груз на верёвке, качели — всё это колебательные системы, подобные маятнику настенных часов. Любая из этих систем способна совершать свободные колебания около положения равновесия. У всех этих колебательных систем возвращающая сила возникает в результате действия силы тяжести.

ФИЗИЧЕСКИЙ МАЯТНИК

Колебательные системы, подобные грузу на верёвке или качелям, представляют собой физические тела разной формы и размеров, которые совершают колебания около точки подвеса или опоры. Такие системы называют физическими маятниками.

МАТЕМАТИЧЕСКИЙ МАЯТНИК

Для изучения свойств колебательного движения обычно рассматривают простейшую систему — математический маятник (нитяной маятник). Это грузик малого размера, подвешенный на длинной тонкой нити. В математическом маятнике пренебрегают массой нити и считают нить нерастяжимой. Также считают, что масса математического маятника — это только масса грузика, а силы упругости действуют только со стороны нити. В данном случае колебательной системой является нить, подвешенное на ней тело, штатив, на котором нить закреплена, и Земля.

Действительно, равнодействующая сила равна векторной сумме всех сил, действующих на тело: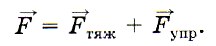Так как складываемые векторы направлены не вдоль одной прямой, их сумму можно найти по правилу параллелограмма. Под действием силы F маятник начнёт двигаться к положению равновесия. По инерции груз пройдёт положение равновесия и отклонится от него в другую сторону. Дойдя до своего крайнего положения, маятник под действием равнодействующей сил начнёт вновь двигаться к положению равновесия. Пройдя его, он опять отклонится. Далее процесс будет повторяться.

ПЕРИОД КОЛЕБАНИЙ

При колебательном движении все положения колеблющегося тела периодически повторяются. Время, за которое совершается одно полное колебание, называют периодом колебаний.

Обозначается период колебаний буквой Т ив СИ измеряется в секундах. На практике период колебаний можно измерить при помощи часов или секундомера.

ЧАСТОТА КОЛЕБАНИЙ

Аналогично периоду и частоте обращения тела по окружности колебательное движение характеризуется не только периодом, но и частотой. Частота колебаний — это число колебаний в единицу времени. Обозначается частота колебаний греческой буквой ν.

Если период колебаний маятника Т = 0,2 с, то это означает, что продолжительность одного полного колебания такого маятника 2 /₁₀ или 1 /₅ с. Тогда за секунду такой маятник совершит пять колебаний, т. е. 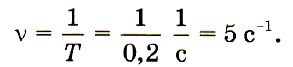Таким образом, частота колебаний является величиной, обратной периоду колебаний.

1 Гц — это частота таких колебаний, при которых за 1 с совершается одно полное колебание.

АМПЛИТУДА КОЛЕБАНИЙ

Ещё одной характеристикой колебательного движения является амплитуда колебаний — наибольшее по модулю смещение тела от положения равновесия.

Обозначается амплитуда колебаний буквой А и измеряется в единицах длины — метрах, сантиметрах и т. д. Зависит амплитуда колебаний от того первоначального толчка или отклонения, при помощи которого маятник был приведён в движение. Для математического маятника в качестве амплитуды надо взять либо длину дуги ОА, либо длину отрезка ОА, либо длину отрезка АС (половина хорды ВА). Дело в том, что для малых амплитуд эти длины практически совпадают.

ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ КОЛЕБАНИЙ

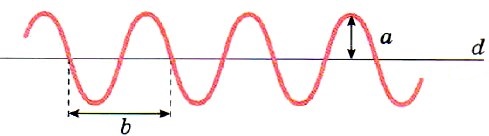
Если в качестве математического маятника использовать воронку с песком или красящей жидкостью, а под колеблющимся маятником равномерно перемещать бумажную ленту, на ней останется характерный след. Вычерченная на ленте за некоторый промежуток времени кривая будет выглядеть так, как показано на рисунке.

Амплитуде колебаний здесь будет соответствовать расстояние а, которое показывает наибольшее отклонение кривой от прямой d, соответствующей состоянию равновесия маятника. Расстояние b соответствует расстоянию, на которое переместится бумажная лента за время, равное периоду колебаний воронки.

Генрих Рудольф Герц (1857—1894) — выдающийся немецкий физик. Его работы сыграли огромную роль в развитии науки и техники и положили начало изобретению беспроволочного телеграфа, радио и телевидения.

Вы смотрели Конспект по физике для 9 класса «Маятник. Характеристики колебательного движения».

Источник

Характеристики колебаний

Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):

Такие величины, как амплитуду и период, можно определить по графику колебаний.

Начальную фазу, так же, определяют по графику, с помощью интервала времени \(\large \Delta t\), на который относительно нуля сдвигается начало ближайшего периода.

Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.

А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.

Что такое амплитуда

Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.

Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.

В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.

Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.

К примеру, пусть колеблется величина \( \large x \). Тогда символом \( \large x_ <0>\) обозначают амплитуду колебаний этой величины.

Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».

С помощью графика амплитуду можно определить так (рис. 2):

Что такое период

Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.

Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.

\( \large T \left( c \right) \) – период колебаний.

Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.

Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Период – это время одного полного колебания.

На графике период найти удобнее одним из таких способов (рис. 4):

Что такое частота

Обозначают ее с помощью греческой буквы «ню» \( \large \nu \).

Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».

Поэтому, размерность частоты — это единицы колебаний в секунду:

\( \large \nu \left( \frac<1> \right) \).

Иногда в учебниках встречается такая запись \( \large \displaystyle \nu \left( c^ <-1>\right) \), потому, что по свойствам степени \( \large \displaystyle \frac<1> = c^ <-1>\).

Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.

Одно колебание в секунду соответствует частоте в 1 Герц.

Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:

Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Что такое циклическая частота

Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол \(\large 2\pi\) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный \(\large 2\pi\) секунд.

Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:

\( \large \displaystyle \omega \left( \frac<\text<рад>> \right) \)

Примечание: Величину \( \large \omega \) так же называют круговой частотой, а еще — угловой скоростью (ссылка).

Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за \(\large 2\pi\) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный \(\large 2\pi\) секунд?».

Обычная \( \large \nu \) и циклическая \( \large \omega \) частота колебаний связаны формулой:

Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.

Чтобы с помощью графика колебаний определить величину \( \large \omega \), нужно сначала найти период T.

Затем, воспользоваться формулой \( \large \displaystyle \nu = \frac<1>\) и вычислить частоту \( \large \nu \).

И только после этого, с помощью формулы \( \large \omega = 2\pi \cdot \nu \) посчитать циклическую \( \large \omega \) частоту.

Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.

Определить величину \( \large \omega \) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный \(\large 2\pi\), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Что такое начальная фаза и как определить ее по графику колебаний

Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.

Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, \(\large \varphi_ <0>\).

\(\large \varphi_ <0>\left(\text <рад>\right) \) — начальная фаза, измеряется в радианах (или градусах).

Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рассмотрим теперь, как величина \(\large \varphi_ <0>\) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.

Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы \(\large \varphi_ <0>\) принимаем равной нулю.

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время \(\large \Delta t\), начальный угол \(\large \varphi_ <0>\) будет отличаться от нулевого значения.

Определим угол \(\large \varphi_ <0>\) с помощью графика колебаний.

Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина \(\large \varphi_ <0>\) — в радианах. Значит, нужно связать формулой кусочек времени \(\large \Delta t\) и соответствующий ему начальный угол \(\large \varphi_ <0>\).

Как вычислить начальный угол по интервалу смещения

Алгоритм нахождения начального угла состоит из нескольких несложных шагов.

\[\large T = 5 – 1 = 4 \left( \text <сек>\right)\]

Из графика следует, что период T = 4 сек.

Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.

Для этого используем формулу:

\(\large \displaystyle \frac<1> <4>\cdot 2\pi = \frac<\pi > <2>=\varphi_ <0>\)

Значит, интервалу \(\large \Delta t\) соответствует угол \(\large \displaystyle \frac<\pi > <2>\) – это начальная фаза для красной кривой на рисунке.

Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:

Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол \(\large \displaystyle \frac<\pi > <2>\) имеет знак «плюс».

Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая \(\large \varphi_ <0>= 0 \).

Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».

А если функция сдвинута вправо и запаздывает относительно обычной функции, величину \(\large \varphi_ <0>\) записываем со знаком «-».

Примечания:

Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.

Что такое фаза колебаний

Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают \(\varphi\).

Различия между фазой и начальной фазой

Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.

Первый угол называют начальной \( \varphi_<0>\) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто \( \varphi\) фазой (рис. 10б) – это величина переменная.

Как на графике колебаний отметить фазу

На графике колебаний фаза \(\large \varphi\) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.

На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.

Как определить фазу с помощью формулы

Пусть нам известны величины \(\large \omega\) — циклическая частота и \(\large \varphi_<0>\) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.

Время колебаний t будет величиной переменной.

Фазу \(\large \varphi\), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:

Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.

Что такое разность фаз

Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.

Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.

\( \large \varphi_<01>\) – для первого процесса и,

\( \large \varphi_<02>\) – для второго процесса.

Определим разность фаз между первым и вторым колебательными процессами:

Величина \(\large \Delta \varphi \) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.

Как связаны характеристики колебаний — формулы

Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.

Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.

\( \large T \left( c \right) \) – время одного полного колебания (период колебаний);

\( \large N \left( \text <шт>\right) \) – количество полных колебаний;

\( \large t \left( c \right) \) – общее время для нескольких колебаний;

\(\large \nu \left( \text <Гц>\right) \) – частота колебаний.

\(\large \displaystyle \omega \left( \frac<\text<рад>> \right) \) – циклическая (круговая) частота колебаний.

\(\large \varphi_ <0>\left( \text <рад>\right) \) — начальная фаза;

\(\large \varphi \left( \text <рад>\right) \) – фаза (угол) в выбранный момент времени t;

\(\large \Delta t \left( c \right) \) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.

Источник