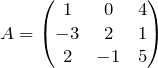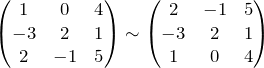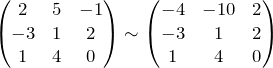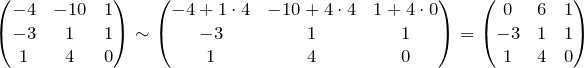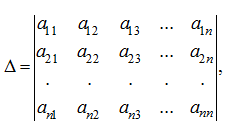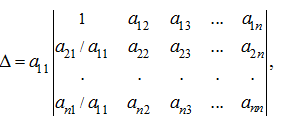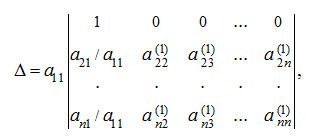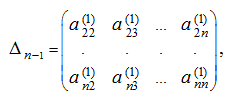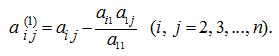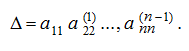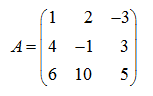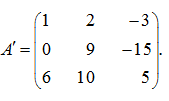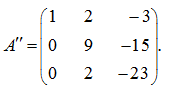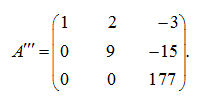Что не относится к элементарным преобразованиям матрицы
12. Элементарные преобразования матрицы
Если размеры 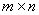
Элементарными преобразованиями матрицы называют следующие:
Перестановка строк (столбцов) матрицы;
Умножение строки (столбца) на число отличное от нуля;
Прибавление к элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.
Целью элементарных преобразований является приведение исходной матрицы к ступенчатой форме. Матрица называется ступенчатой, если для нее выполняются следующие условия:
Если какая – либо строка матрицы состоит из нулей, то и все последующие строки также состоят из нулей;
Если первый, отличный от нуля, элемент какой – либо строки расположен в одном из столбцов данной матрицы, то все элементы этого столбца, расположенные ниже, являются нулевыми.
Матрица из одной строки считается ступенчатой по определению.
Например, матрица 
Теорема (о приведении к ступенчатой матрице).
Любую матрицу можно привести к ступенчатой матрице, выполнив конечное число элементарных преобразований.
Теорема доказывается конструктивно путем перебора конечного числа возможных матриц с нулевыми элементами.
Пример. Приведем к ступенчатому виду следующую матрицу: 
На первом шаге выполним следующие элементарные преобразования над матрицей 


Теорема (о ранге ступенчатой матрицы).
Ранг ступенчатой матрицы равен числу ее ненулевых строк.
Доказательство. Ненулевые, ступенчатые строки линейно независимы, что можно показать, составив линейную комбинацию этих строк и приравняв ее нулевой строке. Покомпонентный анализ этой линейной комбинации показывает, что все числовые коэффициенты при строках, начиная с первой, последовательно обращаются в нули. По определению это означает линейную независимость ненулевых строк. Остальные строки ступенчатой матрицы нулевые, а добавление нулевой строки в систему ненулевых строк превращает новую систему в зависимую систему. Поэтому только ненулевые строки линейно независимы. По следствию 1 теоремы о базисном миноре это означает, что ранг ступенчатой матрицы равен числу ее ненулевых строк, что и требовалось доказать.
Теорема (об элементарных преобразованиях).
Ранг матрицы не изменяется при ее элементарных преобразованиях.
Доказательство. При любых элементарных преобразованиях отличный от нуля определитель остается таковым. Поэтому любой найденный базисный минор останется базисным. Миноры более высокого порядка равны нулю и останутся таковыми при любых элементарных преобразованиях. Таким образом, теорема доказана.
На основе трех, приведенных выше теорем, формулируется метод элементарных преобразований: сначала исходная матрица приводится к ступенчатому виду, затем ранг исходной матрицы полагается равным числу ненулевых строк ступенчатой матрицы.
В рассмотренном выше примере матрица 
Исследуя систему уравнений общего вида, необходимо либо доказать, что она не имеет решений, либо, если она совместна, найти все возможные решения и представить их в компактной и наглядной форме. Для этого систему уравнений с помощью элементарных преобразований приводят к более простому виду, позволяющему непосредственно увидеть решения или показать несовместность системы. При этом центральным понятием является равносильность двух систем. Две системы уравнений с одними теми же неизвестными называются равносильными, если они имеют одно и то же множество решений.
Например, системы 


Системы 

Элементарными преобразованиями системы линейных алгебраических уравнений называют следующие преобразования:
Перестановка местами любых двух уравнений;
Умножение любого уравнения системы на одно и то же число, отличное от нуля;
Сложение любых двух уравнений.
Теорема (о равносильных переходах).
Любое конечное число элементарных преобразований системы переводят ее в систему, равносильную исходной системе.
Доказательство теоремы следует непосредственно из определения элементарных преобразований системы линейных уравнений общего вида.
Как видно из приведенных определений, элементарным преобразованиям системы полностью соответствуют элементарные преобразования строк так называемой
Расширенной матрицы системы 

Элементарные преобразования матрицы
Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.
Содержание
Определение
Элементарными преобразованиями строк называют:
В некоторых курсах линейной алгебры перестановка строк матрицы не выделяется в отдельное элементарное преобразование в силу того, что перестановку местами любых двух строк матрицы можно получить, используя умножение любой строки матрицы на константу 



Аналогично определяются элементарные преобразования столбцов.
Элементарные преобразования обратимы.
Обозначение 


Свойства
Инвариантность ранга при элементарных преобразованиях
| Теорема (об инвариантности ранга при элементарных преобразованиях). Если  , то , то  . . |
Эквивалентность СЛАУ при элементарных преобразованиях
Нахождение обратных матриц
| Теорема (о нахождении обратной матрицы). Пусть определитель матрицы  не равен нулю, пусть матрица не равен нулю, пусть матрица  определяется выражением определяется выражением  . Тогда при элементарном преобразовании строк матрицы . Тогда при элементарном преобразовании строк матрицы  к единичной матрице к единичной матрице  в составе в составе  одновременно происходит преобразование одновременно происходит преобразование  к к  . . |
Приведение матриц к ступенчатому виду
Связанные определения
Элементарная матрица. Матрица А является элементарной, если умножение на нее произвольной матрицы В приводит к элементарным преобразованиям строк в матрице В.
Литература
Полезное
Смотреть что такое «Элементарные преобразования матрицы» в других словарях:
ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ — Введение. Э. ч. в точном значении этого термина первичные, далее неразложимые ч цы, из к рых, по предположению, состоит вся материя. В совр. физике термин «Э. ч.» обычно употребляется не в своём точном значении, а менее строго для наименования… … Физическая энциклопедия
Элементарные частицы — Введение. Э. ч. в точном значении этого термина первичные, далее неразложимые частицы, из которых, по предположению, состоит вся материя. В понятии «Э. ч.» в современной физике находит выражение идея о первообразных сущностях,… … Большая советская энциклопедия
Произведение матрицы на число — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Матрица (математика) — У этого термина существуют и другие значения, см. Матрица. Матрица математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет… … Википедия
Квадратная матрица — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Матрица линейного оператора — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Перемножение матриц — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Произведение матриц — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Разница матриц — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Метод Гаусса — У этого термина существуют и другие значения, см. Метод Гаусса (оптимизация). Метод Гаусса[1] классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью… … Википедия
Элементарные преобразования матриц
К элементарным преобразованиям над строками матриц относятся следующие преобразования:
Если матрица 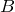
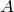
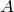
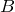
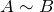
Примеры элементарных преобразований матриц
Продемонстрируем элементарные преобразования строк на примере матрицы
1. Переставим местами первую и третью строки, при этом получится эквивалентная матрица, поэтому между ними ставим знак эквивалентности
2. Умножим первую строку последней матрицы на 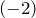
3. Прибавим к первой строке третью, умноженную на 4
Элементарные преобразования строк используются при нахождении ранга матрицы и лежат в основе метода Гаусса.
Эквивалентные преобразования матрицы
В данной публикации мы рассмотрим, что такое элементарные (эквивалентные) преобразования матрицы, какие бывают виды, а также разберем примеры для демонстрации теории на практике.
Определение и виды элементарных преобразований
Элементарными называются такие преобразования матрицы, при которых сохраняется эквивалентность матриц (из-за этого их часто называют эквивалентными). Другими словами такие преобразования не меняют множество решений СЛАУ, которая представлена данной матрицей.
Элементарные преобразования применяются в метода Гаусса, чтобы привести матрицу к треугольному или ступенчатому виду.
К элементарным преобразованиям относятся:
Примечание: аналогичные действия применимы и к столбцам матрицы.
Матрицы A и B являются эквивалентными, если B получена путем элементарных преобразований A (или наоборот). Для обозначения эквивалентности используется специальный символ – “
Примеры эквивалентных преобразований матрицы
Давайте на примере матрицы ниже покажем все виды элементарных преобразований.
1. Поменяем вторую и третью строки местами.
2. Умножим первую строку на число 3.
3. Вычтем из третьей строки удвоенную вторую.
Что не относится к элементарным преобразованиям матрицы
Содержание >> Прикладная математика >> Матричная алгебра >> Основы матричного исчисления >> Элементарные преобразования матриц
Элементарные преобразования матриц
Элементарные преобразования матрицы находят широкое применение в различных математических задачах. Например, они составляют основу известного метода Гаусса (метода исключения неизвестных) для решения системы линейных уравнений [1].
К элементарным преобразованиям относятся:
1) перестановка двух строк (столбцов);
2) умножение всех элементов строки (столбца) матрицы на некоторое число, не равное нулю;
3) сложение двух строк (столбцов) матрицы, умноженных на одно и то же число, отличное от нуля.
Две матрицы называются эквивалентными, если одна из них может быть получена из другой после конечного числа элементарных преобразований. В общем случае эквивалентные матрицы равными не являются, но имеют один и тот же ранг.
Вычисление определителей с помощью элементарных преобразований
С помощью элементарных преобразований легко вычислить определитель матрицы. Например, требуется вычислить определитель матрицы:
где 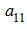
Тогда можно вынести множитель 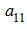
который равен: 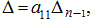
Затем повторяем те же действия для 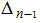
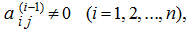
Если для какого-нибудь промежуточного определителя 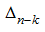
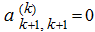
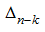
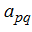
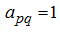
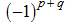
к треугольному виду.
Теперь умножим первую строку на 6, а третью на (–1) и прибавим первую строку к третьей:
Наконец, умножим вторую строку на 2, а третью на (–9) и прибавим вторую строку к третьей:
В результате получена верхняя треугольная матрица