Что не имеет массы в физике

Безмассовые частицы

Безмассовые частицы (люксо́ны) — частицы, масса покоя которых равна нулю. Любая безмассовая частица может двигаться только со скоростью света. Такая частица не может находиться в состоянии покоя: она может родиться (быть излучена), двигаться со скоростью света, затем уничтожиться (поглотиться). Безмассовая частица обладает энергией, которая вычисляется по формуле где p — импульс частицы, а c — скорость света. Термин «безмассовая» не вполне точно отражает природу такой частицы: она имеет массу , которая не связана с её нулевой массой покоя.

Сказанное о невозможности для безмассовой частицы двигаться с иной скоростью, чем скорость света, не относится к виртуальным частицам. Последние могут находиться «вне светового конуса», даже будучи безмассовыми. Впрочем, они не могут быть непосредственно наблюдаемы в таком же качестве, как наблюдаются реальные частицы, в частности, виртуальные частицы не могут использоваться для передачи сигналов быстрее света. Само их существование можно скорее характеризовать как проявляющееся лишь косвенно в виде эффектов, предсказываемых теорией, использующей их в расчетах.

Известные безмассовые частицы

Долгое время считалось, что нулевой массой покоя обладают нейтрино. Однако в настоящее время многочисленные осцилляционные эксперименты с солнечными, атмосферными, реакторными и ускорительными нейтрино надёжно продемонстрировали наличие у них малой, но ненулевой массы покоя.

Ссылки

Полезное

Смотреть что такое «Безмассовые частицы» в других словарях:

Элементарные частицы — Введение. Э. ч. в точном значении этого термина первичные, далее неразложимые частицы, из которых, по предположению, состоит вся материя. В понятии «Э. ч.» в современной физике находит выражение идея о первообразных сущностях,… … Большая советская энциклопедия

ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ — в узком смысле частицы, к рые нельзя считать Состоящими из других частиц. В совр. физике термин Э. ч. используют в более широком смысле: так наз. мельчайшие частицы материи, подчиненные условию, что они не являются атомными ядрами и атомами… … Химическая энциклопедия

глюоны — Безмассовые частицы, обладающие спином 1 и ненулевым цветовым зарядом. Путем обмена ими осуществляется сильное взаимодействие между кварками … Политехнический терминологический толковый словарь

Масса — У этого термина существуют и другие значения, см. Масса (значения). Масса Размерность M Единицы измерения СИ кг … Википедия

Глюон — Символ: g Состав: Элементарная частица Семья: Бозон Группа: Калибровочный бозон Участвует во взаимодействиях: Cильное, гравитационное … Википедия

Фотон — У этого термина существуют и другие значения, см. Фотон (значения). Фотон Символ: иногда … Википедия

СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ — самопроизвольное нарушение симметрии, выражающееся в том, что физ. система, описываемая ур ниями движения, к рые обладают нек рой симметрией, находится в состоянии, лишённом этой симметрии. С. н. с. происходит в тех случаях, когда симметричное… … Физическая энциклопедия

Инвариантная масса — Возможные 4 импульсы тел с нулевой и положительной массой покоя. Векторы 4 импульса, построенные от точки пересечения осей до любой точки на зелёной гиперболе, имеют одну и ту же (положительную) длину, то есть массу частицы, несущей этот… … Википедия

Материя (физика) — У этого термина существуют и другие значения, см. Материя. Материя (от лат. māteria «вещество») объективная реальность, содержимое пространства, одна из основных категорий науки и философии, объект изучения физики. Физика описывает… … Википедия

Физический объект — Материя фундаментальное научное понятие, связанное с любыми объектами, существующими в природе, о которых мы можем судить благодаря нашим ощущениям. Физика описывает материю как нечто, существующее в пространстве и во времени (в пространстве… … Википедия

Источник

Два определения массы, и почему я использую только одно из них

К сожалению, в процессе революции в науке, происходившей с понятиями пространства, времени, энергии, импульса и массы, Эйнштейн, кроме прочего, оставил после себя два различных и противоречащих друг другу определения массы. Из-за этого всё, что мы говорим и имеем в виду, можно интерпретировать двумя очень разными способами. При этом непосредственно в физике никакой путаницы нет. Специалисты точно знают, о чём идёт речь, и знают, как делать предсказания и использовать подходящие уравнения. Весь вопрос только в значении самого слова. Но слова важны, особенно когда мы беседуем о физике с людьми, не являющимися экспертами в этой области, и с учениками, для которых уравнения пока ещё не полностью понятны.

В своих статьях под «массой» я имею в виду свойство объекта, которое иногда ещё называют «инвариантной массой» или «массой покоя». Для нас с моими коллегами по физике частиц это просто старая добрая «масса». Термины «инвариантная масса» или «масса покоя» используются для того, чтобы уточнить, что вы имеете в виду под «массой», только если вы настаиваете на введении второй величины, которую вы тоже хотите называть «массой», и которую обычно называют «релятивистской массой». Специалисты по физике частиц избегают этой путаницы, совсем не используя концепцию «релятивистской массы».

Масса покоя лучше релятивистской в том, что первая масса – это свойство, по поводу величины которого соглашаются все наблюдатели. У объектов не так уж много подобных свойств. Возьмём скорость объекта: разные наблюдатели не согласятся по поводу скорости. Вот едет машина – как быстро она едет? С вашей точки зрения, если вы стоите на дороги, допустим, она едет со скоростью 80 км/ч. С точки зрения водителя машины она не двигается, а двигаетесь вы. С точки зрения человека, едущего навстречу машине, она может двигаться уже со скоростью в 150 км/ч. Выходит, что скорость – величина относительная. Нет смысла спрашивать о скорости машины, ибо нельзя получить ответ. Вы должны спрашивать, какова скорость объекта относительно определённого наблюдателя. У каждого наблюдателя есть право сделать это измерение, но разные наблюдатели получат разные результаты. Принцип относительности Галилея уже включал в себя эту идею.

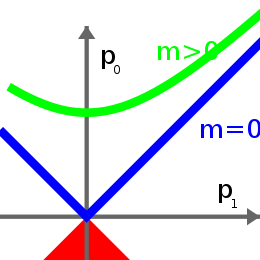
Эти уравнения и их графическое представление подробно разобраны в другой статье.

Мне хочется дать вам понять причины, по которым специалисты по физике частиц используют эти уравнения и не считают, что уравнение E = mc 2 всегда выполняется. Это уравнение относится к тому случаю, в котором наблюдатель не двигается по отношению к объекту. Я попытаюсь сделать это, задав несколько вопросов, ответы на которых сильно различаются в зависимости от выбора значения слова «масса». Это поможет привлечь ваше внимание к большим проблемам в случае существования двух соперничающих определений массы и пояснить, почему в физике частиц гораздо проще работать с массой, не зависящей от наблюдателя.

Имеет ли частица света, фотон, массу или нет?

Но если вы имеете в виду релятивистскую массу – тогда да, имеет. У фотона всегда есть энергия, поэтому у него всегда есть масса. Ни один наблюдатель не увидит его безмассовым. Нулевая у него только инвариантная масса, также известная, как масса покоя. У каждого электрона будет своя масса, и у каждого фотона будет своя. Электрон и фотон, обладающие одной энергией, будут по этому определению обладать одной массой. У некоторых фотонов масса будет больше, чем у некоторых электронов, а у других электронов масса будет больше, чем у других фотонов. Что ещё хуже, для одного наблюдателя масса определённого электрона будет больше массы определённого фотона, а для другого всё может быть наоборот! Поэтому релятивистская масса приводит к путанице.

Действительно ли масса электрона больше, чем масса атомного ядра?

Если вы используете моё определение массы – то нет, никогда. Все наблюдатели согласятся с тем, что масса электрона в 1800 раз меньше массы протона или нейтрона, из которых состоит ядро.

Но если под массой подразумевать релятивистскую, то ответ будет: это зависит от ситуации. Масса электрона в покое меньше. У очень быстрого электрона – больше. Можно даже устроить всё таким образом, что масса электрона будет в точности совпадать с массой выбранного ядра. В общем можно сказать только то, что масса покоя электрона меньше, чем масса покоя ядра.

Есть ли масса у нейтрино?

При использовании моего понятия массы, ответ на этот вопрос был неизвестен с 1930-х годов, когда впервые была предложена концепция нейтрино, до 1990-х. Сегодня нам известно (почти наверняка), что у нейтрино масса есть.

Но если под массой подразумевать релятивистскую, то ответ будет: естественно, мы знали об этом с самого первого дня существования понятия «нейтрино». У всех нейтрино есть энергия, так что, как и у фотонов, у них есть масса. Вопрос лишь в наличии инвариантной массы.

У всех ли частиц одного типа – к примеру, у всех фотонов, у всех электронов, у всех протонов, у всех мюонов – одинаковая масса?

При использовании моего понятия массы, ответ на этот вопрос будет утвердительным. Все частицы одного типа обладают одинаковой массой.

Но если под массой подразумевать релятивистскую, то ответ будет: очевидно, нет. Два электрона, движущихся с разными скоростями, обладают разной массой. У них одинаковая только инвариантная масса.

Истинна ли старая формула Ньютона F = ma, соотносящая массу, воздействие и ускорение?

При использовании моего понятия массы, ответ будет: нет. В эйнштейновской версии относительности эта формула исправлена.

Но если под массой подразумевать релятивистскую, то ответ будет: это зависит от ситуации. Если вектора сила и движения частицы перпендикулярны, тогда да; в ином случае – нет.

Увеличивается ли масса частицы с увеличением скорости и энергии?

При использовании моего понятия массы, ответ будет: нет. Смотрите график выше. Разные наблюдатели могут назначить частице разную энергию, но все согласятся с её массой.

Но если под массой подразумевать релятивистскую, то ответ будет: да. Разные наблюдатели могут назначить частице разную энергию, и, следовательно, разные массы. Согласятся они только по поводу инвариантной массы.

Итак, мы по меньшей мере видим наличие лингвистической проблемы. Если мы не обозначим точно, какое из определений массы мы используем, мы получим совершенно разные ответы на простейшие вопросы физики. К сожалению, в большинстве книг для непрофессионалов и даже в некоторых учебниках для первого курса университета (!) авторы переключаются туда и сюда между этими терминами без пояснений. И самая распространённая путаница среди моих читателей связана с тем, что им сообщают два типа сведений о массе, противоречащих друг другу: один подходит для массы покоя, другой – для релятивистской. Очень плохо использовать одно слово для двух разных вещей.

Это, конечно, всего лишь язык. С языком можно делать всё, что угодно. Определения и семантика не имеют значения. Когда физик вооружён уравнениями, язык становится неидеальным носителем. Математика никогда не путается, и человек, понимающий математику, тоже не запутается.

Но для большинства людей и для начинающих студентов это кошмар.

Что делать? Один вариант – настаивать на использовании всех возможных терминов. Но из-за этого объяснения будут очень запутанными.

• Энергия покоящегося объекта = инвариантной массе умноженной на с 2 = релятивистской массе умноженной на с 2
• Масса движущегося объекта = инвариантной массе, как и раньше, но энергия = релятивистской массе помноженной на с 2 у него больше, чем ранее, из-за энергии движения.

Это слишком многословно. Мы с коллегами просто говорим:

Такой способ не менее содержателен, в нём используется меньше различных концепций и определений, он избегает двух противоречивых значений слова «масса», одно из которых не меняется с движением, а другое – меняется.

С точки зрения лингвистики, семантики и концепций, необходимо избегать понятия «релятивистская масса» и убрать слова «инвариантная» и «покоя» из определений «инвариантная масса» и «масса покоя» потому, что «релятивистская масса» – бесполезная концепция. Это просто другое название для энергии частицы. Использовать понятие «релятивистской массы» – это то же самое, как настаивать на термине «красновато-синий». Если я начну настаивать на использовании термина «красновато-синий» для описания изюма, вы возразите: но у нас уже есть слово для этого цвета: пурпурный. Что с ним не так? И ещё вы можете сказать: «Говорить, что цвет изюма – это разновидность синего цвета, неправильно и это запутывает. Можно сделать вывод, что цвет изюма немного похож на цвет неба, а на самом деле они отличаются». Примерно в таком же ключе релятивистская масса помноженная на с 2 — это просто другое название энергии (для которой у нас уже есть подходящее слово), и описывать энергию так, будто это что-то вроде массы, значит, запутывать читателя.

Величина справа явно не нуждается в новом названии, поскольку это явно ни E, ни p – она не сохраняется, как E и p, но она не зависит от наблюдателя (в отличие от E и p!)

Понятие «релятивистской массы» появилось не на пустом месте и не из какой-то глупости. Его ввёл сам Эйнштейн, и не зря, поскольку он имел дело с отношениями между энергией системы объектов и массой этой системы. Но хотя понятие релятивистской массы пропагандировалось и распространялось другими знаменитыми физиками того времени, сам Эйнштейн, судя по всему, отбросил такой способ мышления, и тоже не зря. Так же поступило сообщество современных специалистов по физике частиц.

Источник

Масса

Ма́сса (от греч. μάζα ) — скалярная физическая величина, одна из важнейших величин в физике. Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. Тесно связана с понятиями «энергия» и «импульс» (по современным представлениям — масса эквивалентна энергии покоя).

В современной физике понятие «количество вещества» имеет другой смысл, а концепцию «массы» можно трактовать несколькими способами:

Прямые обобщения понятия массы включают в себя тензорные присоединённую массу и эффективную массу — как характеристики инерциальных свойств системы «тело плюс среда» в гидродинамике и квантовой теории. В квантовой теории рассматриваются также поля с нестандартными кинетическими членами, например, поле Хиггса, которые можно рассматривать как поля, масса квантов которых зависит от их энергии.

Содержание

Принцип эквивалентности

Все явления в гравитационном поле происходят точно так же, как в соответствующем поле сил инерции, если совпадают напряжённости этих полей и одинаковы начальные условия для тел системы.

Гравитационная масса — характеристика материальной точки при анализе в классической механике, которая полагается причиной гравитационного взаимодействия тел, в отличие от инертной массы, которая определяет динамические свойства тел.

Как установлено экспериментально, эти две массы пропорциональны друг другу. Не было обнаружено никаких отклонений от этого закона, поэтому новых единиц измерения для инерционной массы не вводят (используют единицы измерения гравитационной массы) и коэффициент пропорциональности считают равным единице, что позволяет говорить и о равенстве инертной и гравитационной масс.

Можно сказать, что первая проверка пропорциональности двух видов массы была выполнена Галилео Галилеем, который открыл универсальность свободного падения. Согласно опытам Галилея по наблюдению свободного падения тел, все тела, независимо от их массы и материала, падают с одинаковым ускорением свободного падения. Сейчас эти опыты можно трактовать так: увеличение силы, действующей на более массивное тело со стороны гравитационного поля Земли, полностью компенсируется увеличением его инертных свойств.

Следует различать «слабый принцип эквивалентности» и «сильный принцип эквивалентности». Сильный принцип эквивалентности можно сформулировать так: в каждой точке пространства-времени в произвольном гравитационном поле можно выбрать локально-инерциальную систему координат, такую, что в достаточно малой окрестности рассматриваемой точки законы природы будут иметь такую же форму, как и в не ускоренных декартовых системах координат, где под «законами природы» подразумевают все законы природы.
Слабый принцип отличается тем, что слова «законы природы» заменяются в нем словами «законы движения свободно падающих частиц». Слабый принцип — это не что иное, как другая формулировка наблюдаемого равенства гравитационной и инертной масс, в то время как сильный принцип представляет собой обобщение наблюдений за влиянием гравитации на любые физические объекты.

Определение массы

В специальной теории относительности под массой понимают модуль 4-вектора импульса [5] :

,

где E — полная энергия свободного тела, p — его импульс, c — скорость света.

В случае произвольной метрики пространства-времени (как в общей теории относительности) это определение требует некоторого обобщения:

Здесь — метрический тензор, — 4-импульс.

Определённая выше масса является релятивистским инвариантом, то есть она одна и та же во всех системах отсчёта. Если перейти в систему отсчёта, где тело покоится, то — масса определяется энергией покоя.

Особенно просто выглядят эти определения в системе единиц, в которой скорость света принята за 1 (например, в планковской или же в принятой в физике элементарных частиц системе единиц, в которой масса, импульс и энергия измеряются в электронвольтах):

В СТО: В ОТО:

Следует, однако, отметить, что частицы с нулевой массой (фотон и гипотетический гравитон) двигаются в вакууме со скоростью света (c ≈ 300000 км/сек), и поэтому не существует системы отсчёта, в которой бы они покоились. Напротив, частицы с ненулевой массой всегда движутся медленнее скорости света.

В нерелятивистской классической механике — масса есть величина аддитивная (масса системы равна сумме масс составляющих её тел) и инвариантная относительно смены системы отсчёта. В релятивистской механике масса неаддитивная, но тоже инвариантная величина, определяемая, как абсолютная величина 4-вектора энергии-импульса.

О «массе покоя» и «релятивистской массе»

В современной терминологии термин масса применяется вместо терминов инвариантная масса или масса покоя, являясь полностью эквивалентным им по смыслу. В некоторых ситуациях (особенно в популярной литературе) это, однако, уточняется явно, чтобы избежать путаницы из-за понимания термина масса в другом — устаревшем — смысле, описанном в этом параграфе.

Полным аналогом классического определения импульса через массу и скорость в СТО следует считать ковариантное равенство:

, где m — инвариантная масса, а u_μ — 4-скорость (производная от 4-координаты по собственному времени частицы ; единичный вектор, направленный вдоль мировой линии частицы).

Также можно записать ковариантный эквивалент второго закона Ньютона:

, где — 4-ускорение (кривизна мировой линии частицы).

Масса составных и нестабильных систем

Масса элементарной частицы постоянна, и одинакова у всех частиц данного типа и их античастиц. Однако масса массивных тел, составленных из нескольких элементарных частиц (например, ядра или атома) может зависеть от их внутреннего состояния. В частности, для устойчивых систем масса системы всегда меньше суммы масс её элементов на величину, называемую дефектом массы, и равную энергии связи, делённой на квадрат скорости света.

Для системы, подверженной распаду (например, радиоактивному), величина энергии покоя определена лишь с точностью до постоянной Планка, делённой на время жизни: . При описании такой системы при помощи квантовой механики удобно считать массу комплексной, с мнимой частью равной означенному Δm.

Классификация частиц по значению массы

Масса известных на сей день частиц является, в общем, неотрицательной величиной, и должна быть равна нулю для тела, движущегося со скоростью света (фотон). Понятие массы особенно важно для физики элементарных частиц, так как позволяет отделять безмассовые частицы (всегда двигающиеся со скоростью света) от массивных (скорость которых всегда ниже скорости света). Кроме того, масса практически однозначно позволяет идентифицировать частицу (с точностью до зарядового сопряжения).

Положительная масса

К частицам с положительной массой (тардионам) относятся почти все частицы Стандартной модели: лептоны, кварки, W- и Z-бозоны. Эти частицы могут двигаться с любой скоростью, меньшей скорости света, в том числе покоиться. К тардионам относятся также все известные составные частицы: протон, нейтрон, гипероны и мезоны.

Нулевая масса

К известным на сегодняшний день частицам нулевой массы (безмассовым, люксонам) относятся фотоны и глюоны, а также гипотетические гравитоны. Такие частицы в свободном состоянии могут двигаться только со скоростью света. Но поскольку из квантовой хромодинамики следует, что глюоны в свободном состоянии не существуют, то непосредственно наблюдать движущимися со скоростью света можно только фотоны (собственно, именно поэтому её называют скоростью света). Долгое время считалось, что нейтрино также имеют нулевую массу, однако обнаружение вакуумных нейтринных осцилляций свидетельствует о том, что масса нейтрино хоть и очень мала, но не равна нулю.

Следует отметить, что комбинация нескольких частиц нулевой массы может (а в случае, например, сцепленных частиц — должна) иметь ненулевую массу.

Отрицательная масса

Мнимая масса

В рамках специальной теории относительности математически возможно существование частиц с мнимой массой, так называемых тахионов. Такие частицы будут иметь реальные значения энергии и импульса, а их скорость должна всегда быть выше скорости света. Однако допущение возможности наблюдения одиночных тахионов вызывает ряд методологических трудностей (например, нарушение принципа причинности), поэтому в большинстве современных теорий одиночные тахионы не вводятся. Впрочем, в квантовой теории поля мнимая масса может быть введена для рассмотрения тахионной конденсации, не нарушающей принцип причинности.

Единицы измерения массы

В системе СИ масса измеряется в килограммах. Единицей измерения массы в системе СГС является грамм ( 1 ⁄₁₀₀₀ килограмма). Вообще говоря, в любой системе измерения выбор основных (первичных) физических величин, их единиц измерения и их число произволен — зависит от принимаемого соглашения и масса не всегда входит в их состав — так в системе МКГСС единица массы была производной единицей и измерялась в кГс/м•с² (обозначалась как «т. е. м.» или «инерта»). В атомной физике принято сравнивать массу с атомной единицей массы, в физике твёрдого тела — с массой электрона, в физике элементарных частиц массу измеряют в электронвольтах. Кроме этих единиц, используемых в науке, существует большое разнообразие исторических единиц измерения массы, которые сохранили свою отдельную сферу использования: фунт, унция, карат, тонна и др. В астрономии единицей для сравнения масс небесных тел служит масса Солнца.

Измерение массы

Этимология и история понятия

Долгое время одним из главных законов природы считался закон сохранения массы. Однако в XX веке выяснилось, что этот закон является ограниченным вариантом закона сохранения энергии, и во многих ситуациях не соблюдается.

Источник