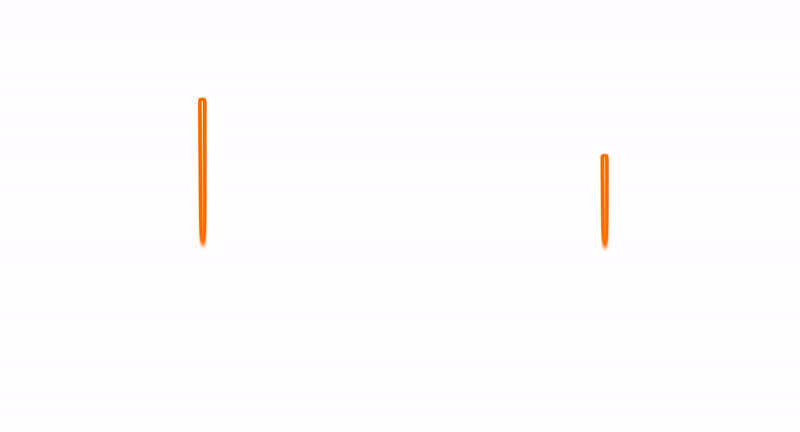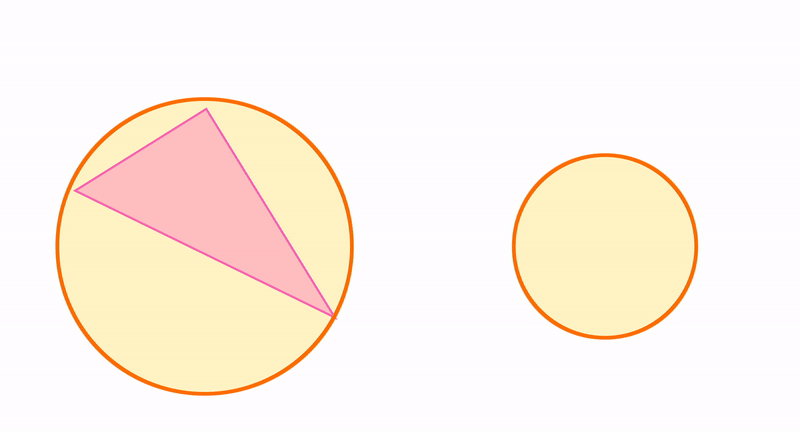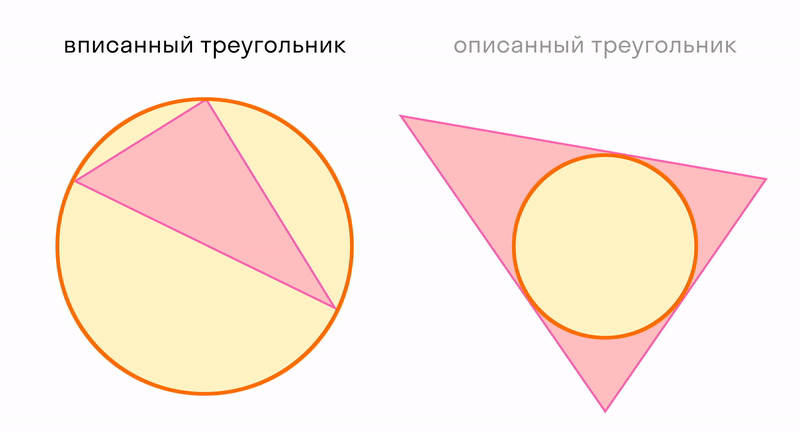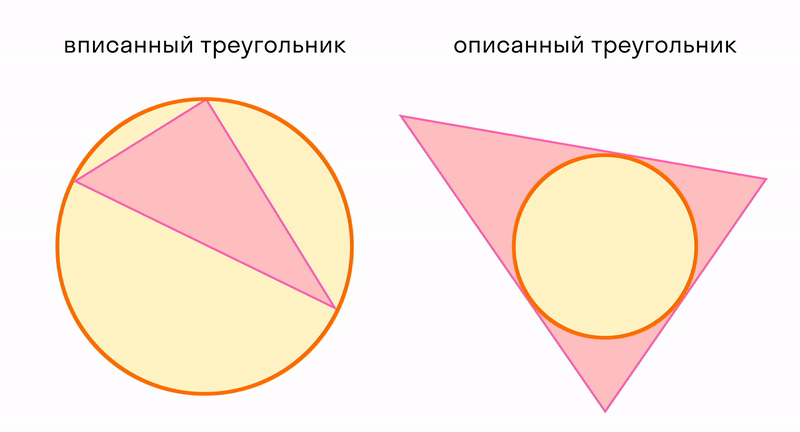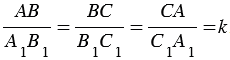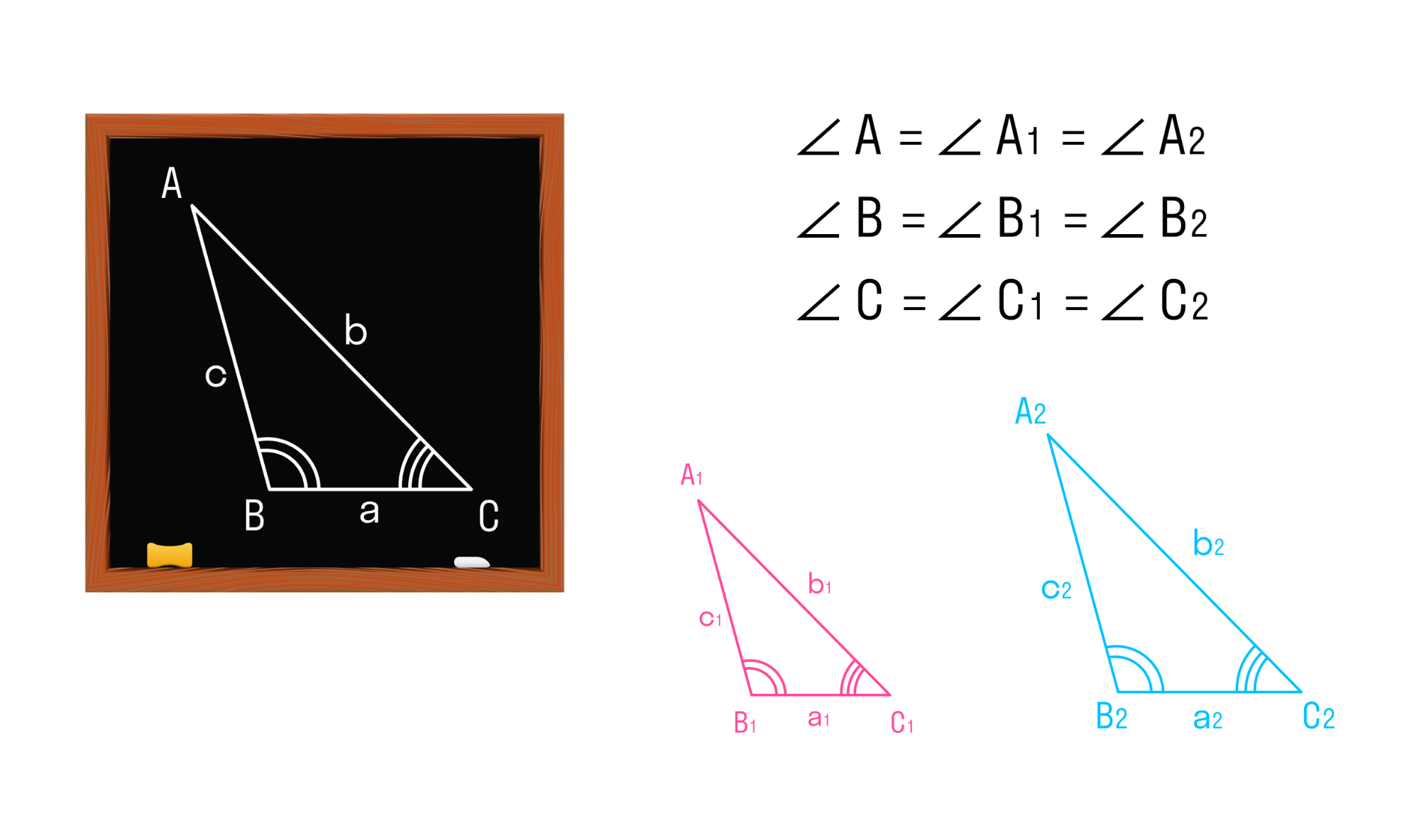Что не доказывается в геометрии

О теоремах, данных без доказательств

Я учился в математической школе. Учился весьма посредственно, но, например, те, кого вовсе отчисляли, переходя в обычную школу, стабильно учились там на отлично без малейшего напряжения мозга.

Однажды для меня стало большим откровением, что в обычных школах некоторые теоремы и формулы давались без доказательства. То есть, людям просто говорили, что есть теорема Фалеса, а есть — формула Герона. А потом сразу давали задачи, которые можно было решить с их использованием. Это для меня было абсолютным разрывом мозга. Это не укладывалось в голове. Я совершенно не мог понять, какой смысл в том, чтобы проходить формулу, не выводя её — это же тогда просто бессмысленный набор букв и знаков. Ну или максимум «занимательный факт»: британские учёные выяснили, что.

Нас, помню, развлекал учитель математики, читая на перемене вопросы билетов экзамена по геометрии из какой-то там другой школы. Идея того, что в ответ на вопрос нужно тупо по памяти написать формулу или формулировку теоремы, представлялась смешной всему классу.

Позже в университете для некоторых моих одногруппников казалось странной необходимость доказывать теоремы или выводить формулы. По школьной привычке учить формулы наизусть эти люди учили наизусть и вывод формул, не понимая, что там происходит. При этом многие из них благодаря прилежности хорошо писали контрольные; боялись же они экзамена. У меня история была обратная: всегда было очень трудно попасть на экзамен, потому, что для этого надо было сдать зачёт, а чтобы допуститься на него, нужно было написать все контрольные в семестре. Терпения же и внимательности на решение практических задачек всегда не хватало.

Экзамены по математике в университете я сдавал на 4, 4, 4 и 5 (в четвёртом семестре была теория функции комплексного переменного, которую я обожаю).

Каждый раз, когда я сдавал листочек с ответами Олегу Геннадьевичу, напротив большинства пунктов задания он ставил минус. Потом, когда он вызывал меня отвечать, он спрашивал: почему не решили эту задачу? Я говорил: забыл формулу такую-то и откуда она берётся. Он говорил: ну, а если бы знали формулу, что бы делали? Я отвечал: нашёл бы то-то, подставил бы в формулу, выразил бы это через это и получил бы ответ. Он подсказывал: ну, вот если вы возьмёте то-то, представите это как сумму этого и этого, а потом домножите на то-то, то вы увидите, как вывести формулу. Я садился, выводил формулу, и он ставил мне плюсик, не дожидаясь, пока я решу собственно задачу. Потом мы переходили к следующему пункту. Почему, спрашивал он, не доказали теорему? Я говорил: я знаю, что при соблюдении таких-то условий она вытекает из того-то через то-то и то-то, но совершенно не помню, как от вот этой формулы делается переход дальше. Он говорил: ну дак дальше из того-то следует, что так-то и так-то. А! перебивал его я, ну точно же, и тогда мы сможем заменить это на это, и там то-то то-то сократится и останется как раз то, что нам нужно!

Люди учившие всё наизусть, частенько уходили с двойками, даже если на листочке напротив всего стояли плюсы: когда в ходе разговора выяснялось, что человек не соображает, листочек уже не имел никакого значения. Он ценил понимание больше прилежности, и понимающему человеку готов был прощать лень и плохую подготовку, за что я ему очень благодарен.

Теорема и её доказательство, формула и её вывод, данные в неразрывной связке, воспитывают навык видеть во всём здравый смысл. Не обязательно знать это всё наизусть, чтобы сформировать правильное отношение к математике. Важно, что математика существовала бы, даже если бы не было Пифагора и Фалеса, Эйлера и Коши, Остроградского и Гаусса. Всё работает так, как работает, с неизбежностью, а не потому, что кто-то так придумал.

Когда люди учат в школе теоремы без доказательств, они потом твердят, что факториал нуля равен 1 по определению. Знающие же то, что математика существует независимо от того, что написано в определениях, понимают, что факториал нуля равен 1 объективно, и он оставался бы равен 1, даже если бы об этом никто не написал в определении.

В математике так много разделов и направлений, и они так сильно взаимосвязаны, что практически невозможно придумать способ последовательного изложения всего этого, чтобы никогда не было необходимости ссылаться вперёд. Нужно быть готовым, что иногда тебе придётся поверить во что-то на слово, а уже позже убедиться, что это действительно так. Человек же, приученный всегда верить на слово, про вторую часть мгновенно забывает.

Источник

Что такое аксиома и теорема

Решение всех задач в геометрии построено на логических рассуждениях. С их помощью мы решаем задачи или выводим новые доказательства.

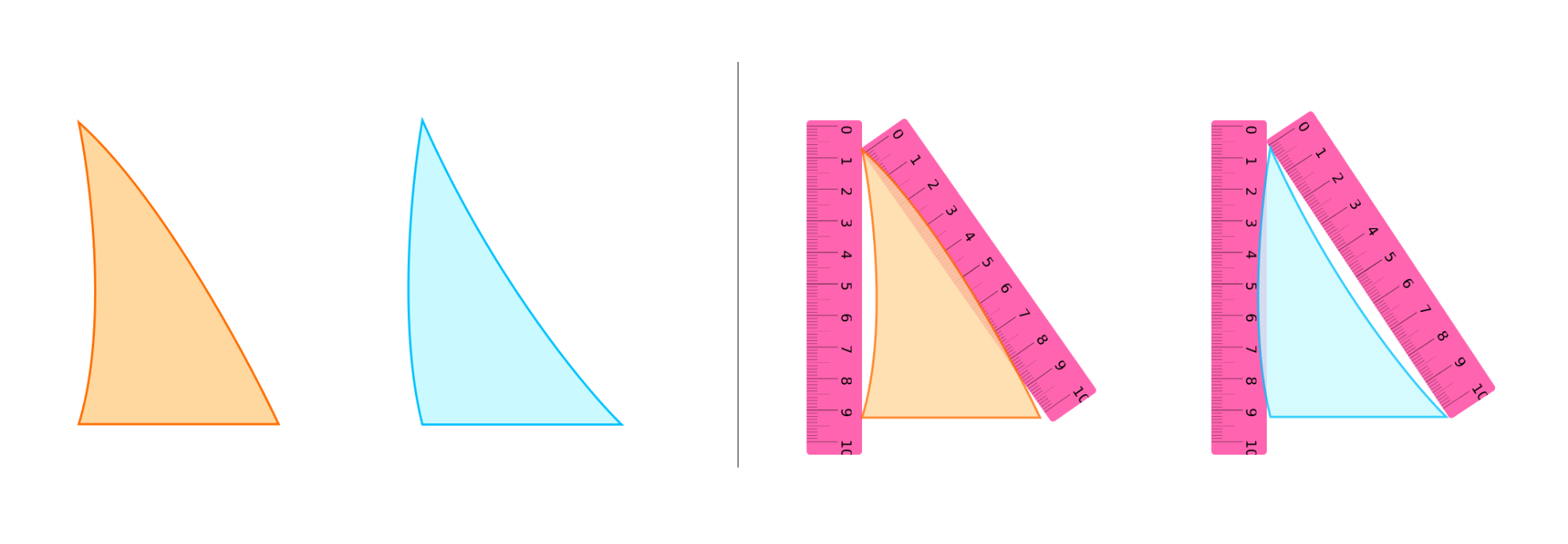
Некоторые из утверждений в геометрии мы используем не задумываясь. Вспомним высказывание, которое мы слышим при самом первом знакомстве с геометрией:
«Через две точки можно провести прямую, и притом только одну».

Но можно ли считать подобное рассуждение доказательством?

Другими словами, утверждение «Через две точки можно провести прямую, и притом только одну» не является доказанным только потому, что мы нарисовали рисунок и по рисунку «на глаз» стало все понятно.

В геометрии действует принцип: «Не верь глазам своим, пока не докажешь утверждение с помощью рассуждений».

Но что нам в таком случае делать? Ведь при решении задач мы используем какие-то очевидные утверждения, не задумываясь об их истинности.

Что такое аксиома

Слово аксиома произошло от древнегреческого слова «axioma» — утверждение, положение.

С точки зрения учащихся, аксиома — лёгкий способ получить отличную оценку. Достаточно просто выучить формулировку. Ведь никаких доказательств для аксиомы учить не требуется.

Всего в геометрии насчитывается около 15 аксиом. В школьном курсе используются далеко не все. Некоторые из них используются в школьном курсе как само собой разумеющееся для нас. Приведем некоторые примеры довольно известных аксиом из школьного курса геометрии:

Что такое теорема

Совсем по-другому обстоят дела с теоремами. Слово теорема происходит от древнегреческого слова «theorema» — смотреть, рассматривать какое-либо утверждение.

Теоремы менее «любимы» учащимися, чем аксиомы. Если учитель попросит рассказать теорему, будет недостаточно, как для аксиомы, сообщить только её формулировку. Потребуется также дать доказательство теоремы.

Примеры формулировок теорем:

Каждое слово или предлог в формулировке играет существенную роль в передаче смысла выражения. Даже просто поменяв порядок слов можно сильно изменить смысл утверждения.

Помните, что все формулировки в геометрии были выверены несколькими тысячами лет развития математики лучшими умами планеты и не терпят никаких словесных изменений.

Что такое лемма

Среди теорем выделяют такие теоремы, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.

Лемма происходит от древнегреческого слова «lemma» – предположение.

Что такое следствие в геометрии

Приведем примеры следствий из аксиомы о параллельности прямых:

Если подытожить все вышесказанное, то сравнивая геометрию с высотным домом, можно представить, что:

Каждая доказанная теорема служит основанием доказательства для следующей теоремы. Именно поэтому так важно изучать геометрию последовательно, переходя с самых основ (аксиом) к теоремам.

Невозможно понять геометрию 9 и 10 класса, не выучив аксиомы и теоремы 7 и 8 класса.

Источник

Что такое аксиома, теорема и доказательство теоремы

Понятие аксиомы

Аксиома — это правило, которое считают верным и которое не нужно доказывать. В переводе с греческого «аксиома» значит принятое положение — то есть взяли и договорились, что это истина, с которой не поспоришь.

Аксиоматический метод — это подход к получению знаний, при котором сначала разрабатывают аксиомы, а потом с их помощью формулируют новые теории.

Синоним аксиомы — постулат. Антоним — гипотеза.

Основные аксиомы евклидовой геометрии

Учить наизусть эти аксиомы не обязательно. Главное — помнить о них и держать под рукой, чтобы при доказательстве теоремы сослаться на одну из них.

А теперь давайте рассмотрим несколько аксиом из геометрии за 7 и 8 класс.

Самая известная аксиома Евклида — аксиома о параллельных прямых. Звучит она так:

Это значит, что если дана прямая и любая точка, которая не лежит на этой прямой, то через неё можно провести только одну единственную прямую, которая будет параллельна этой первой данной прямой.

У этой аксиомы два следствия:

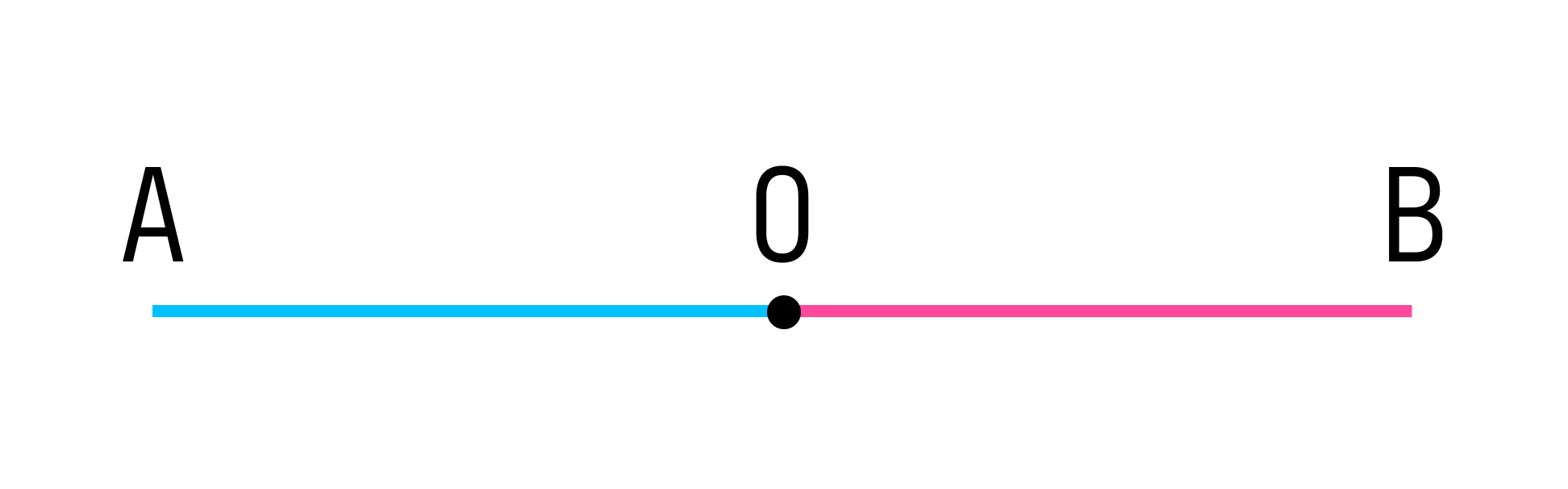
Аксиома Архимеда заключается в том, что, если отложить достаточное число раз меньший из двух отрезков, то можно покрыть больший из них. Звучит так:

Если на прямой есть меньший отрезок А и больший отрезок B, то, можно сложить А достаточное количество раз, чтобы покрыть B.

На картинке можно увидеть, как это выглядит:

Из этого следует, что не существует бесконечно малых и бесконечно больших величин. В качестве математической формулы аксиому можно записать так: А + А + … + А = А * n > В, где n — это натуральное число.

Понятие теоремы

Что такое аксиома мы уже поняли, теперь узнаем определение теоремы.

Теорема — логическое следствие аксиом. Это утверждение, которое основано на аксиомах и общепринятых утверждениях, которые были доказаны ранее, и доказывается на их основе.

Состав теоремы: условие и заключение или следствие.

Среди теорем выделяют такие, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.

Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы. Пример леммы: если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.

Следствие — утверждение, которое выводится из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.

Примеры следствий из аксиомы о параллельности прямых:

Доказательство теоремы — это процесс обоснования истинности утверждения.

Каждая доказанная теорема служит основанием доказательства для следующей теоремы. Именно поэтому так важно изучать геометрию последовательно, переходя от аксиом к теоремам.

Способы доказательства геометрических теорем

Часть аналитического способа — доказательство от противного, когда для доказательства данного предложения убеждают в невозможности предположения противоположного.

Приемы для доказательства в геометрии:

Обратная теорема — это такой перевертыш: в ней условие исходной теоремы дано заключением, а заключение — условием.

Прямая и обратная теорема взаимно-обратные. Например:

В первой теореме данное условие — это равенство сторон треугольника, а заключение — равенство противолежащих углов. А во второй всё наоборот.

Противоположная теорема — это утверждение, в котором из отрицания условия вытекает отрицание заключения.

Вот, как выглядит взаимное отношение теорем на примере:

В геометрическом изложении достаточно доказать только две теоремы, тогда остальные справедливы без доказательства.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Теоремы без доказательств

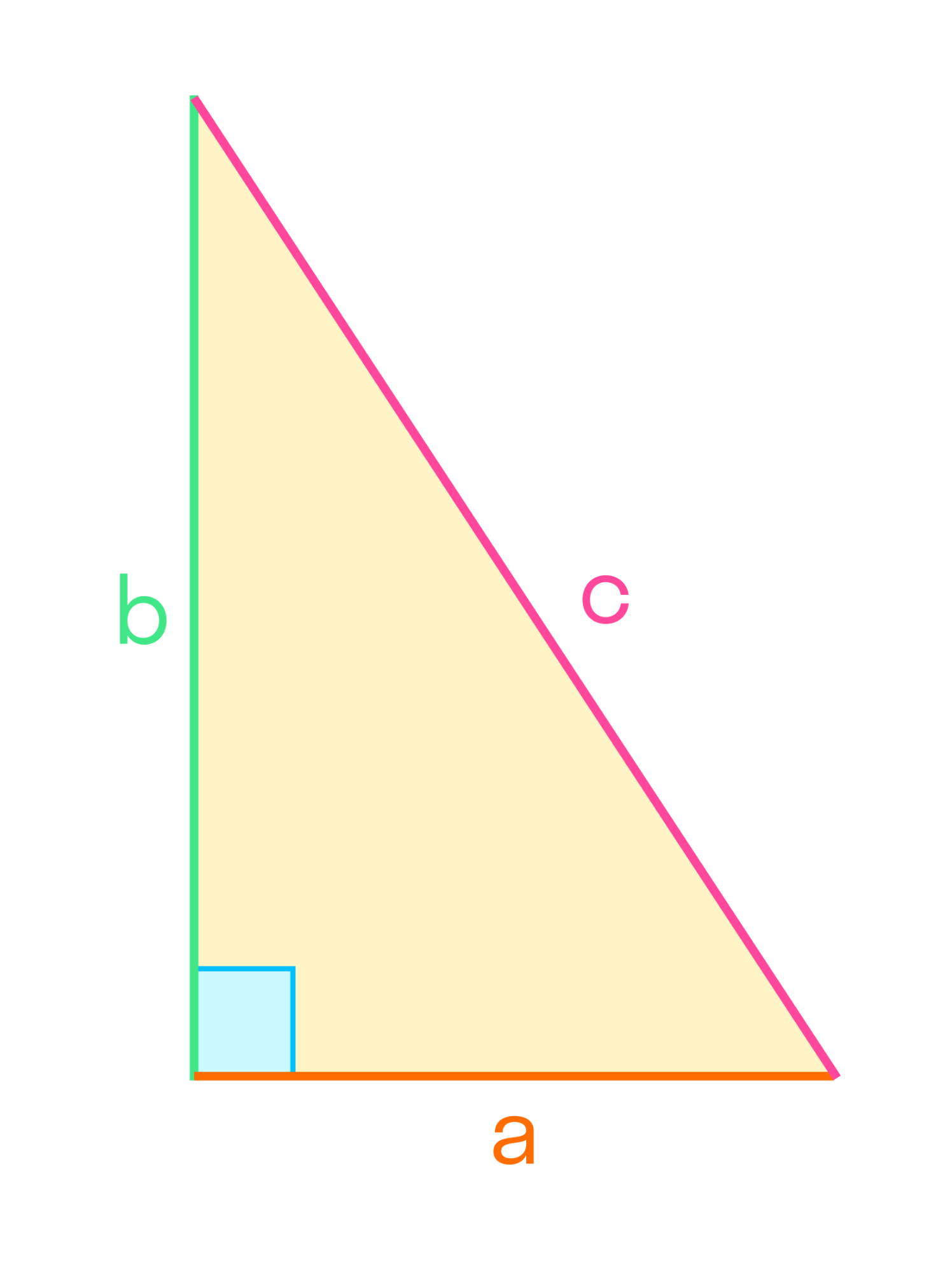
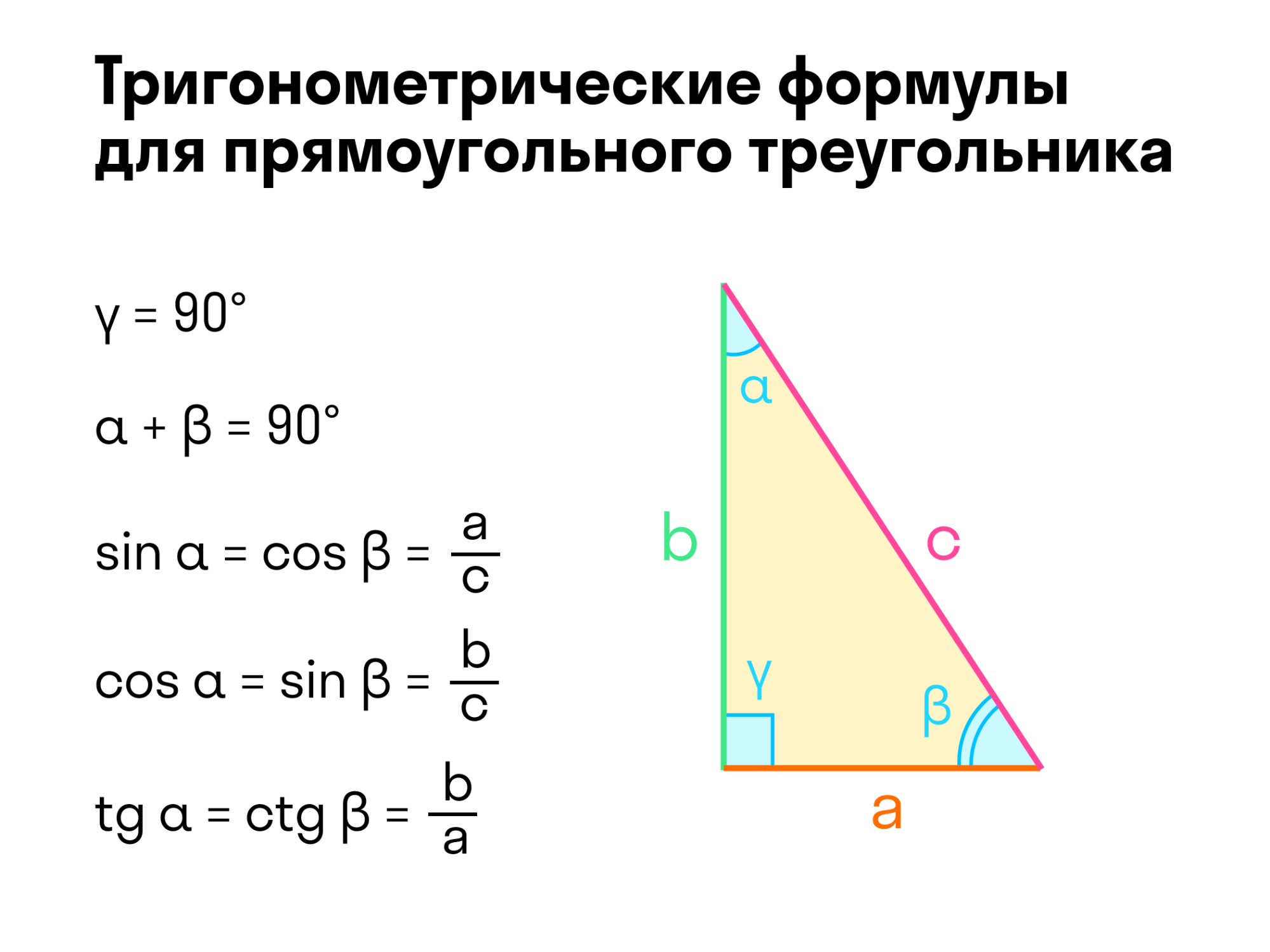
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

Доказательств может быть несколько. Одно из них звучит так: если построить квадраты на сторонах прямоугольного треугольника, то площадь большего из них равна сумме площадей меньших квадратов. На картинке понятно, как это работает:

Теорема косинусов: квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. В виде формулы это выглядит так:

где a, b и c — стороны плоского треугольника,

α — угол, противолежащий стороне а.

Следствия из теоремы косинусов:

Понятия свойств и признаков

У нас есть список аксиом и мы уже знаем, что такое теорема и как ее доказывать. Есть два типа утверждений среди теорем, которые часто встречаются при изучении новых фигур: свойства и признаки.

Свойства и признаки — понятия из обычной жизни, которые мы часто используем.

Свойство — такое утверждение, которое должно выполняться для данного типа объектов. У ноутбука есть клавиатура — это свойство есть у каждого ноутбука. А у электронной книги такого свойства нет.

Примеры геометрических свойств мы уже знаем: у квадрата все стороны равны. Это верно для любого квадрата, поэтому это — свойство.

Такое свойство можно встретить у другого четырехугольника. И клавиатура может быть на других устройствах, помимо ноутбука. Из этого следует, что свойства не обязательно должны быть уникальными.

Признак — это то, по чему мы однозначно распознаем объект.

Звезды в темном небе — признак того, что сейчас ночь. Если человек ходит с открытым зонтом — это признак того, что сейчас идет дождь. При этом ночью не обязательно должны быть видны звезды, иногда может быть облачно. Значит это не свойство ночи.

А теперь вернемся к геометрии и рассмотрим четырехугольник ABCD, в котором AB = BD = 10 см.

Является ли равенство диагоналей признаком прямоугольника? У такого четырехугольника, где AB = BD, диагонали равны, но он не является прямоугольником. Это свойство, но не его признак.

Но если в четырехугольнике противоположные стороны параллельны AB || DC и AD || BC и диагонали равны AB = BD, то это уже верный признак прямоугольника. Смотрите рисунок:

Иногда свойство и признак могут быть эквивалентны. Лужи — это верный признак дождя. У других природных явлений не бывает луж. Но если приходит дождь, то лужи на асфальте точно будут. Значит, лужи — это не только признак, но и свойство дождя.

Такие утверждения называют необходимым и достаточным признаком.

Источник

Какие геометрические факты можно использовать на ЕГЭ без доказательства?

Нужно уметь применять всем знакомые факты, видеть рисунок и решать больше задач. Но вопрос из заголовка задают очень часто, и ответить на него нужно. Естественно, все сотни признаков и свойств, что есть в вашем школьном учебнике можно использовать. Но как насчет более редких фактов: что можно применять без доказательства, а что нет? Точный ответ: любые факты из школьных учебников, рекомендованных минобром на 2017-2018 год.

Ну а вот заветный список того, что мне все-таки удалось обнаружить в соответствующих учебниках:

→ Теорема Менелая (Атанасян. Геометрия 7-9 классы)
→ Теорема Чевы (Атанасян. Геометрия 7-9 классы)
→ Теорема Птолемея (Мерзляк. Геометрия 8 класс)
→ Прямая Эйлера (Мерзляк. Геометрия 8 класс)
→ Теорема об окружности Эйлера (Бутузов. Геометрия 8 класс)
→ Формула медианы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Формула биссектрисы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Теорема о четырех замечательных точках трапеции (Шарыгин. Геометрия 7-9 классы)

Формулу радиуса вневписанной окружности используйте. Каноническое уравнение эллипса — да пожалуйста! Ключевые формулы метода координат для задачи №14, опять же, есть

Но если здесь есть коллеги по цеху, которые могут уточнить еще несколько популярных вопросов насчет непопулярной теории — черкните, буду признателен! Вот интересующие факты: формула Брахмагупты, теорема Стюарта, формула Эйлера для расстояния между центрами вписанной и описанной окружностями треугольника, понятие определителя квадратной матрицы.

Ну и еще раз в заключение. Вероятность того, что задача ЕГЭ не решается без экзотики, равна нулю (такие события называются невозможными). Вероятность того, что вам вообще попадется конфигурация, для которой актуальна, например, теорема о девяти точках окружности, приблизительно равна 0,015. Вероятность того, что школьник в целом знает что-то «запрещенное», приблизительно равна, не кидайтесь камнями, 0,000037.

Источник

Основы геометрии

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Идеальные объекты

Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.

Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.

Все эти фигуры обладают двумя свойствами:

Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.

У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.

Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).

Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.

Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.

Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.

Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.

Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Базовые геометрические объекты

Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.

Точка — это идеальный математический объект, у которого нет длины и ширины.

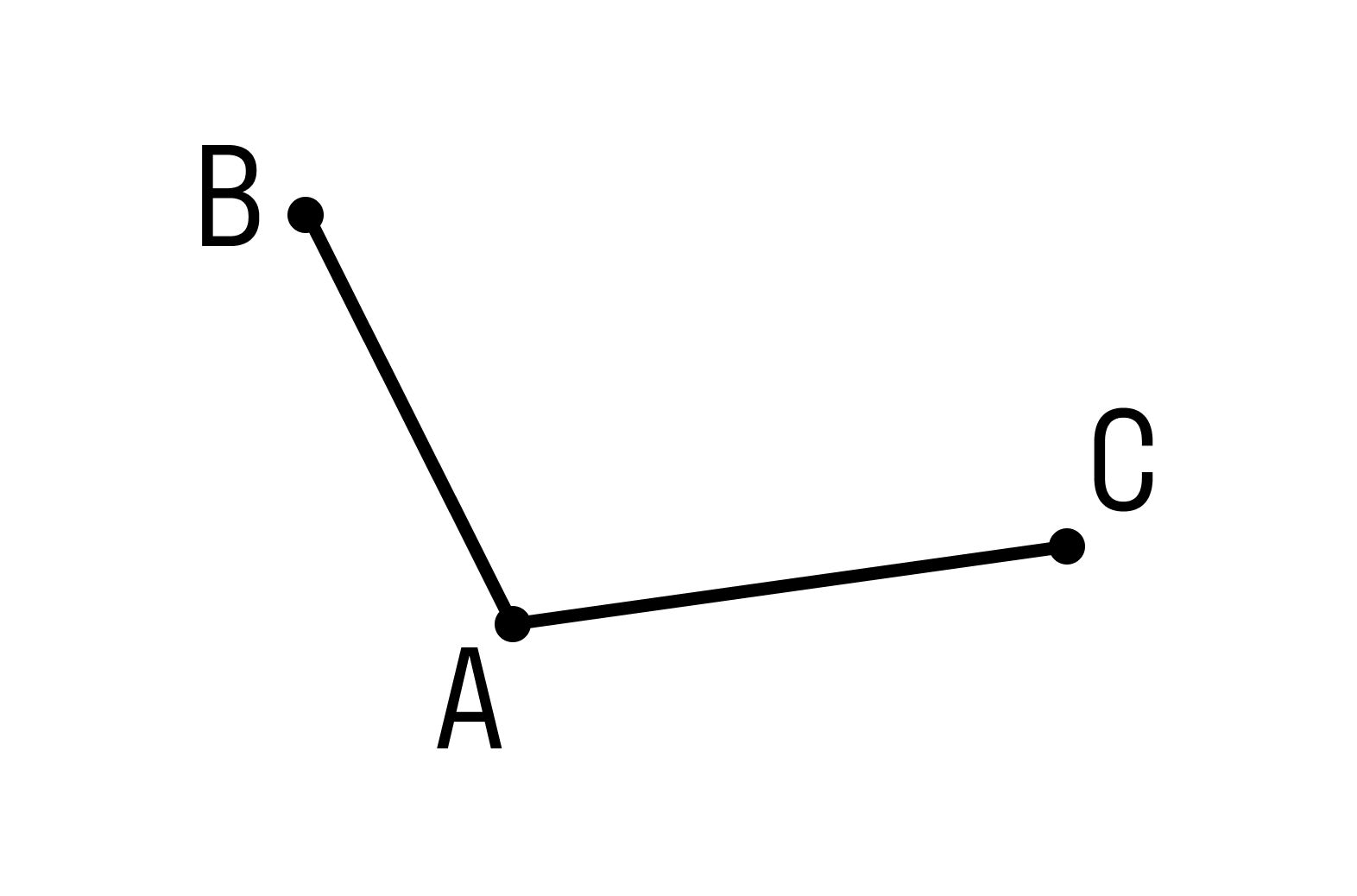
Отрезок — это часть прямой, у которого есть начало и конец.

Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.

Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.

Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.

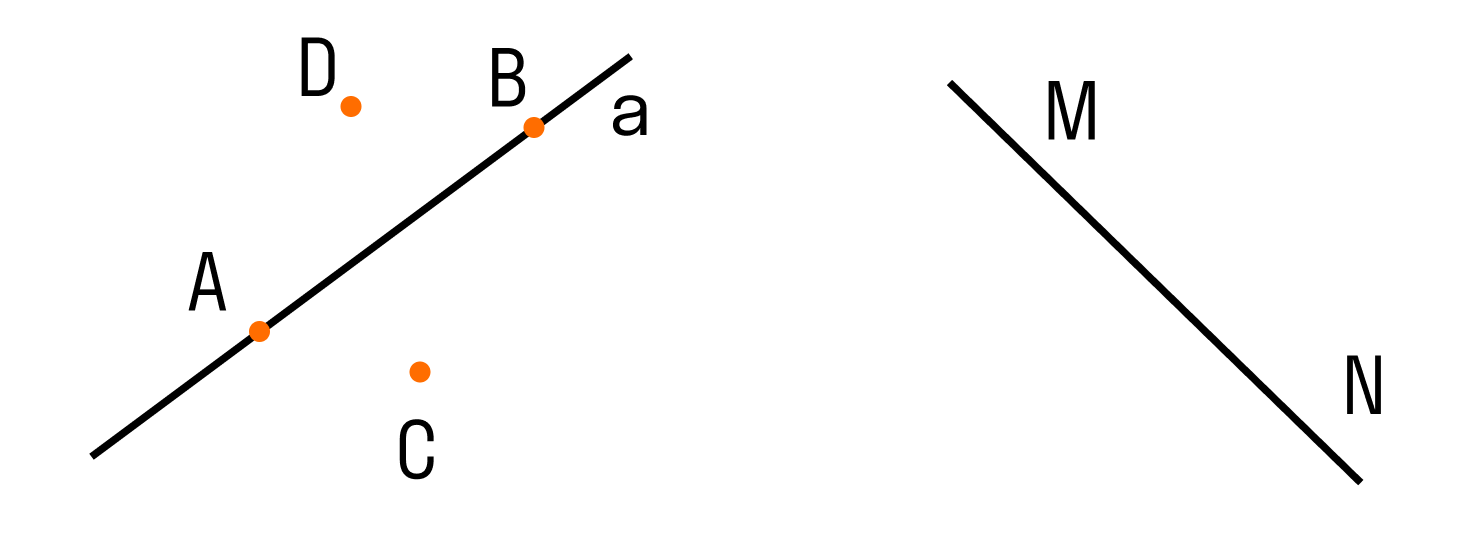
Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).

Два варианта расположения точек относительно прямой:

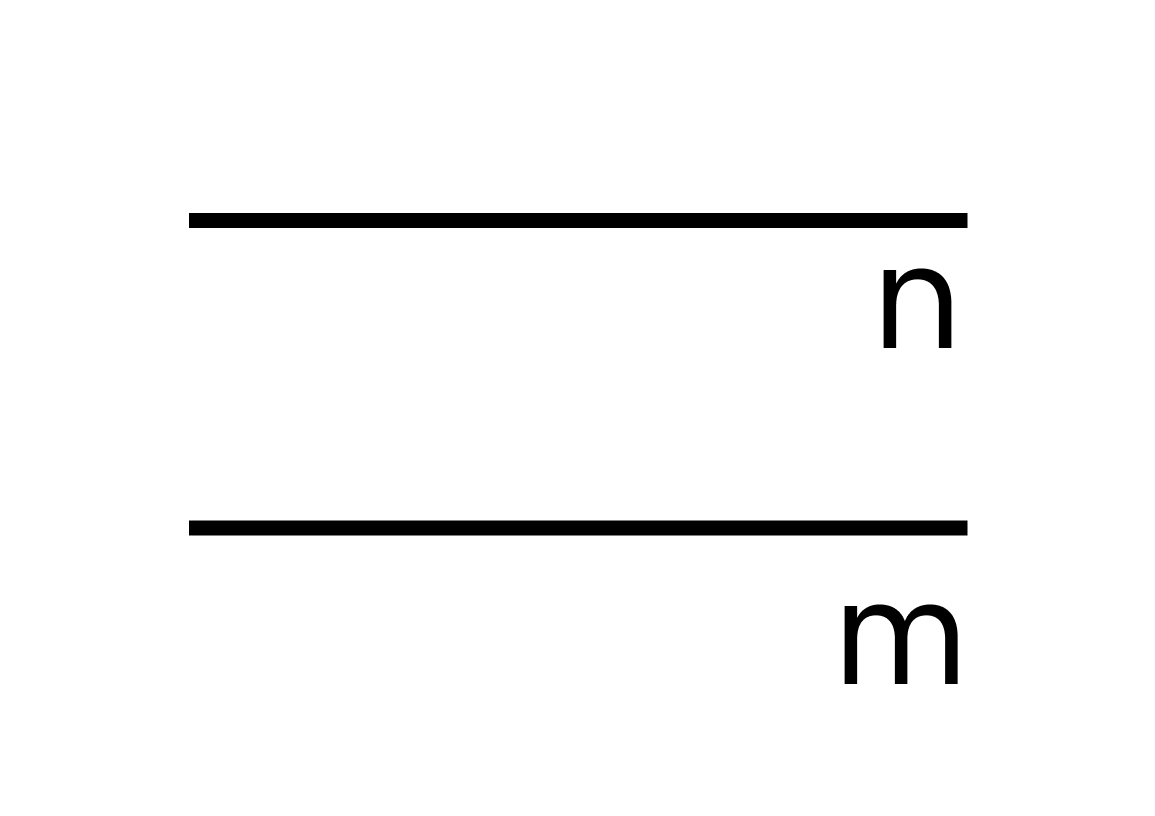
Если рассмотреть две прямые, то возможны два варианта их расположения:

Для записи не пересекающихся прямых используют специальный знак — ,
то есть m n (читают: прямая m не пересекает прямую n).

Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.

На рисунке точка О разбивает прямую АВ на две части:

Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.

Назовем получившиеся лучи:

Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.

Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости

Комбинации простейших объектов

Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).

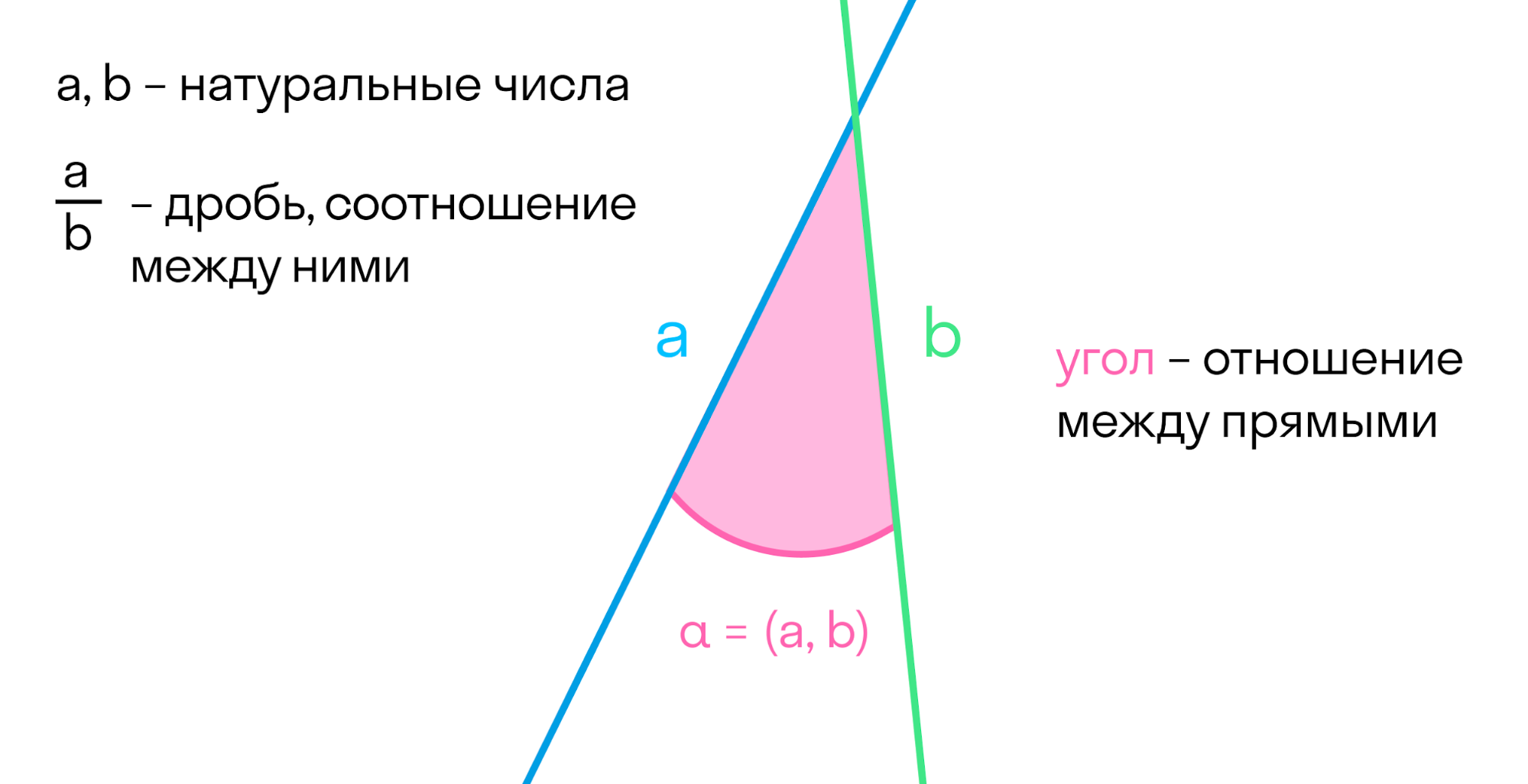
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.

Точно так же мы изучали множества, а после — отношения между множествами, функции.

Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.

Максимальный угол – это полный оборот, он составляет 360 градусов.

Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.

Есть разные виды углов, выделим самые часто встречающиеся:

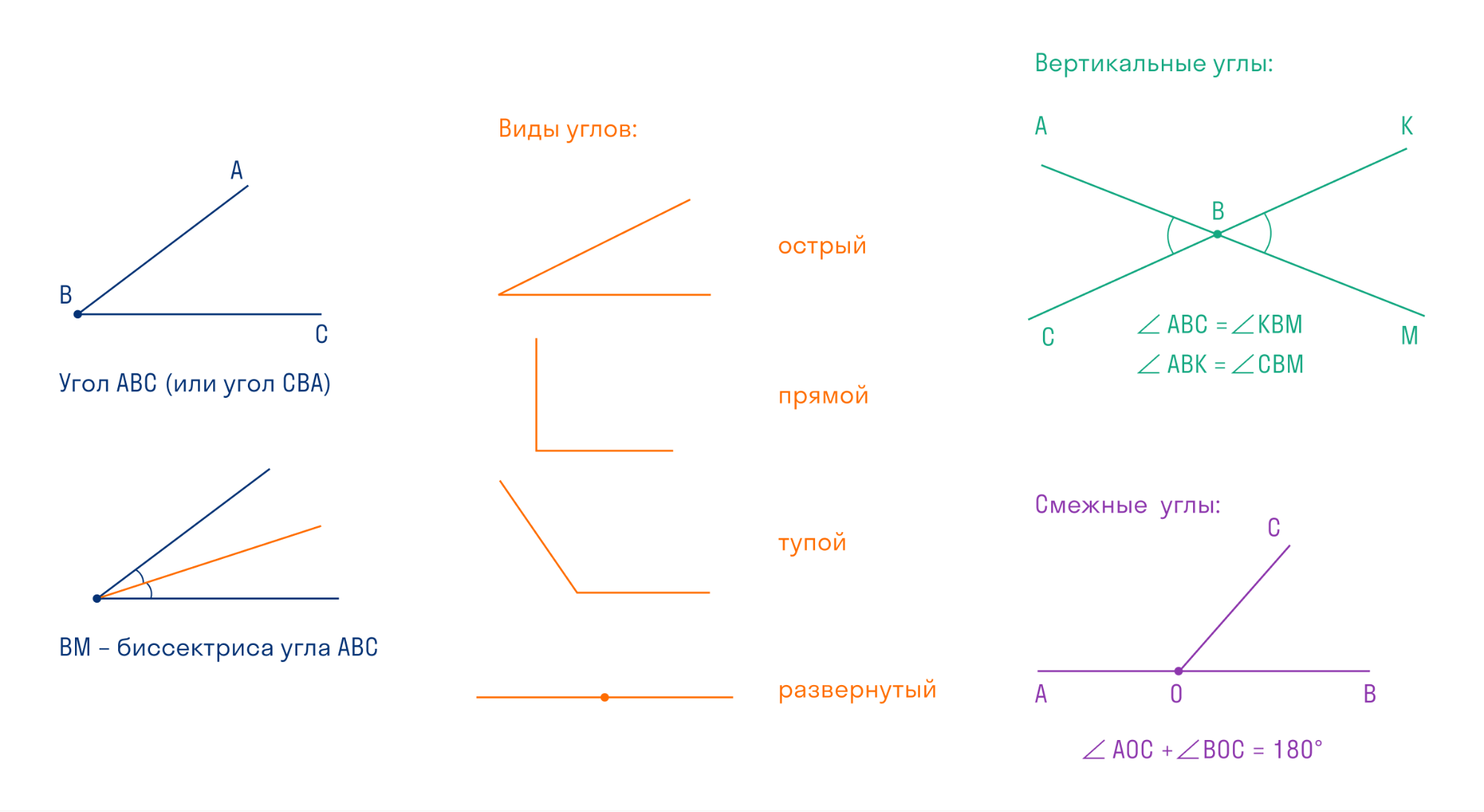
Точка называется вершиной угла, а лучи — сторонами угла.

Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.

Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.

Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.

А теперь посмотрим на взаимное расположение трех прямых.

Первый случай: все три прямые параллельны.

Второй случай: две прямые параллельны, а третья их пересекает.

Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.

Треугольник

Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.

Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.

Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.

Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:

Приходи на наши онлайн уроки по математике с лучшими препадавателями! Для учеников с 1 по 11 классы!

Свойства треугольников

Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.

Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.

Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.

Сумма любых двух сторон треугольника больше его третьей стороны.

Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.

Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.

Равенство треугольников ABC и A₁B₁C₁ обозначается так: ΔABC = ΔA₁B₁C₁.

Есть даже специальные теоремы про равенство треугольников.

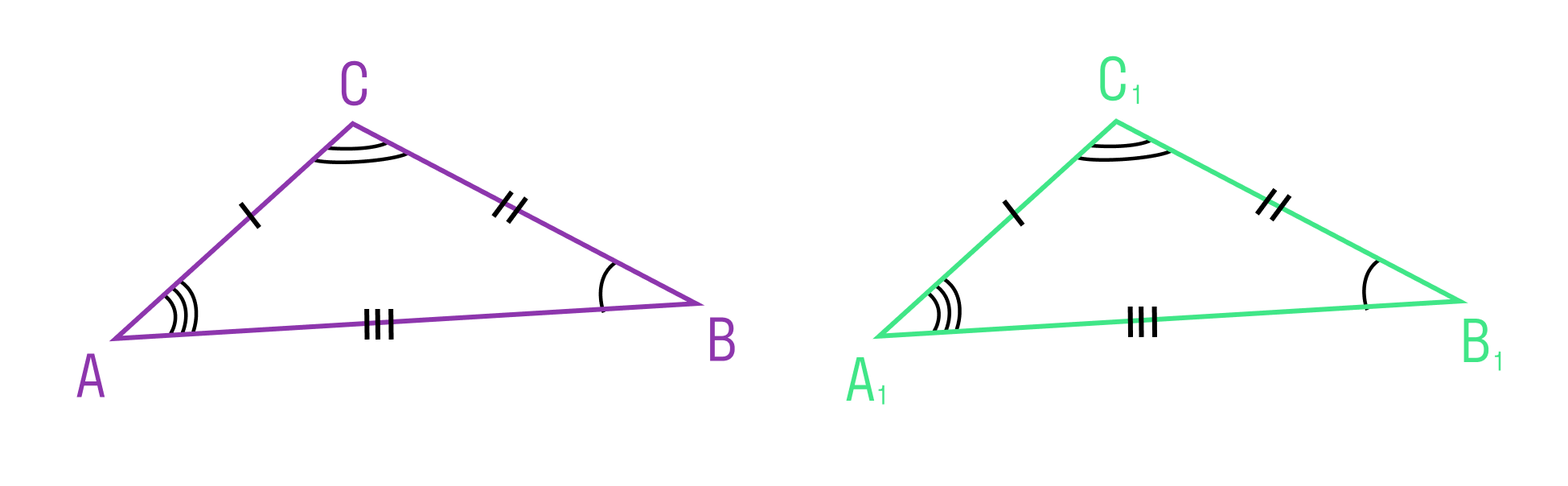
Первый признак равенства треугольников звучит так:

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны

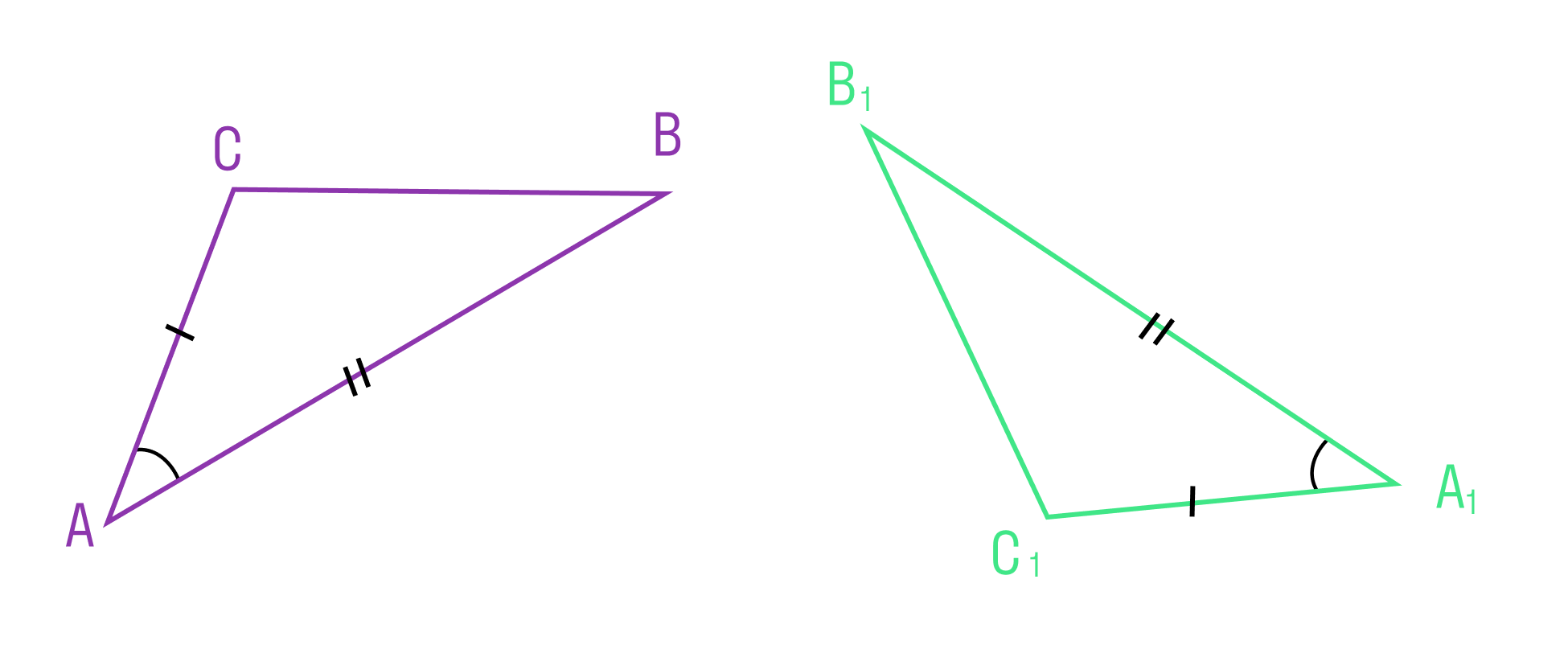
Второй признак равенства треугольников

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

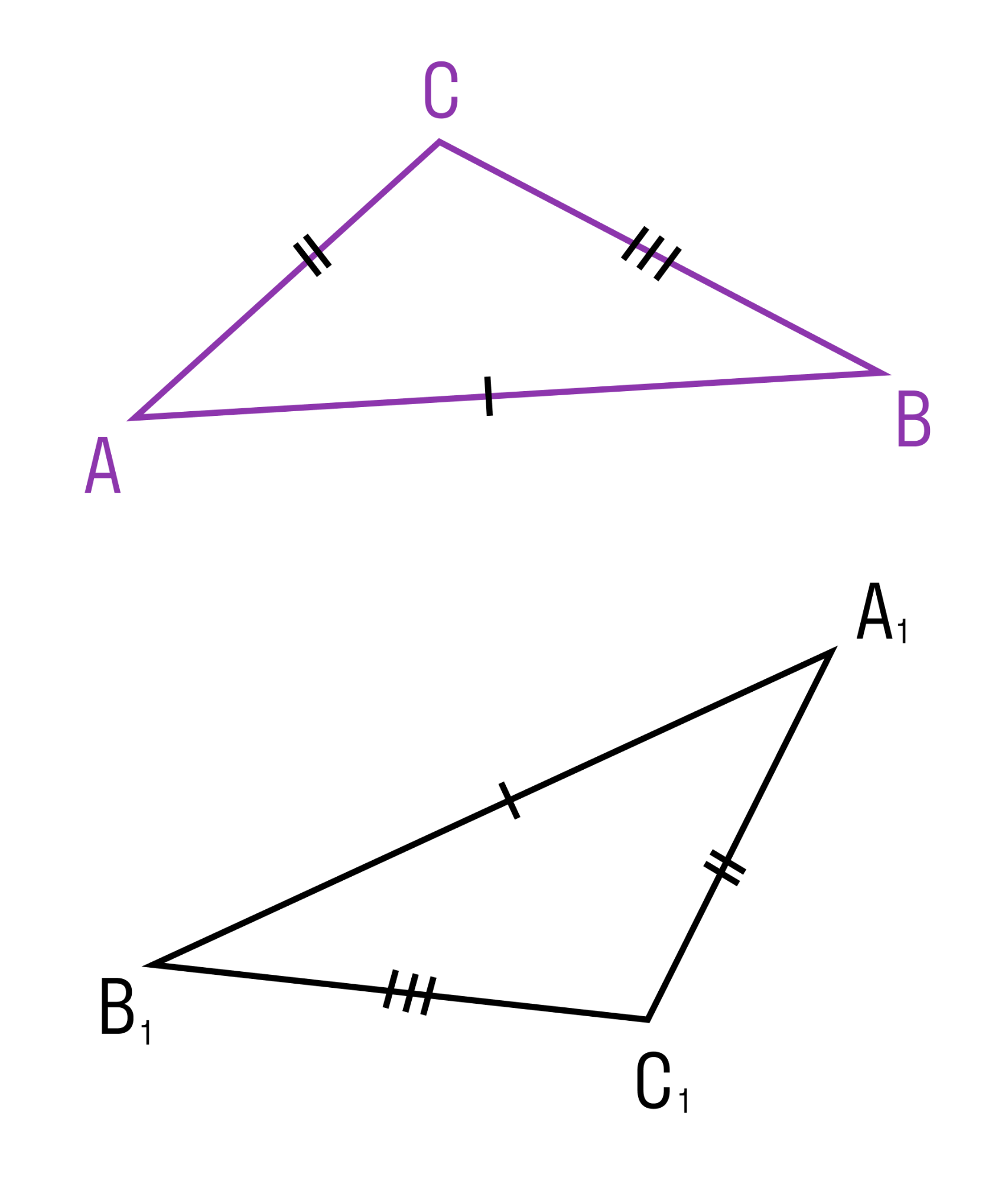
Третий признак равенства треугольников

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.

Подобные треугольники

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

Треугольники АВС и A₁B₁C₁ будут подобны, если

Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.

Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A₁B₁C₁ подобны, это можно записать так: ΔАВС ∾ ΔA₁B₁C₁.

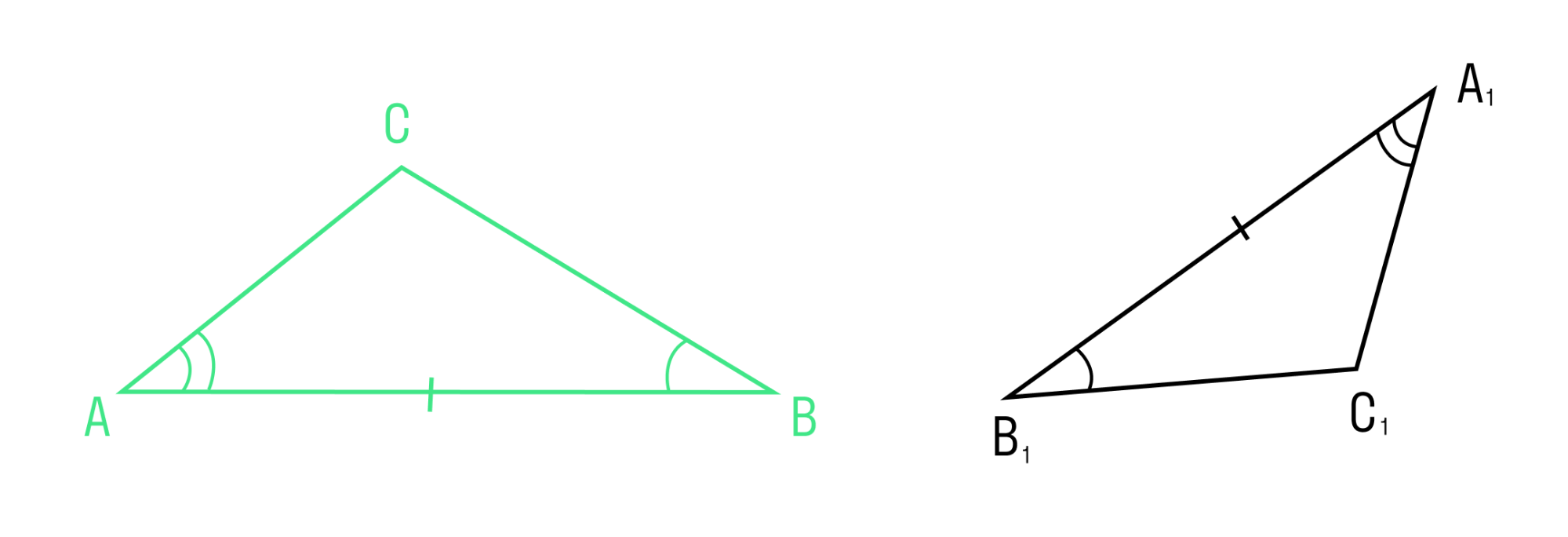
Теорема о первом признаке подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.

Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.

Третий признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

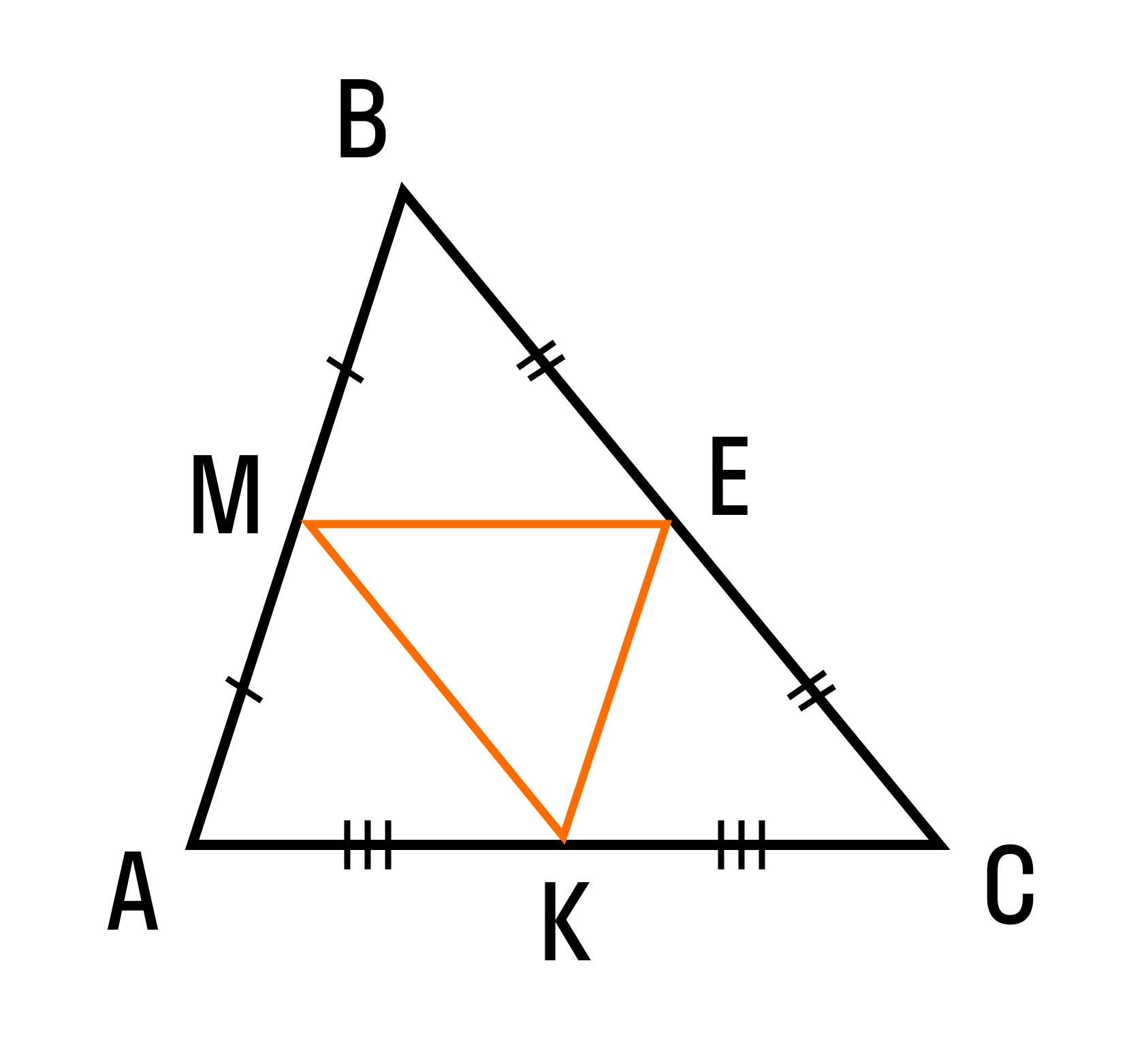
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.

На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны.

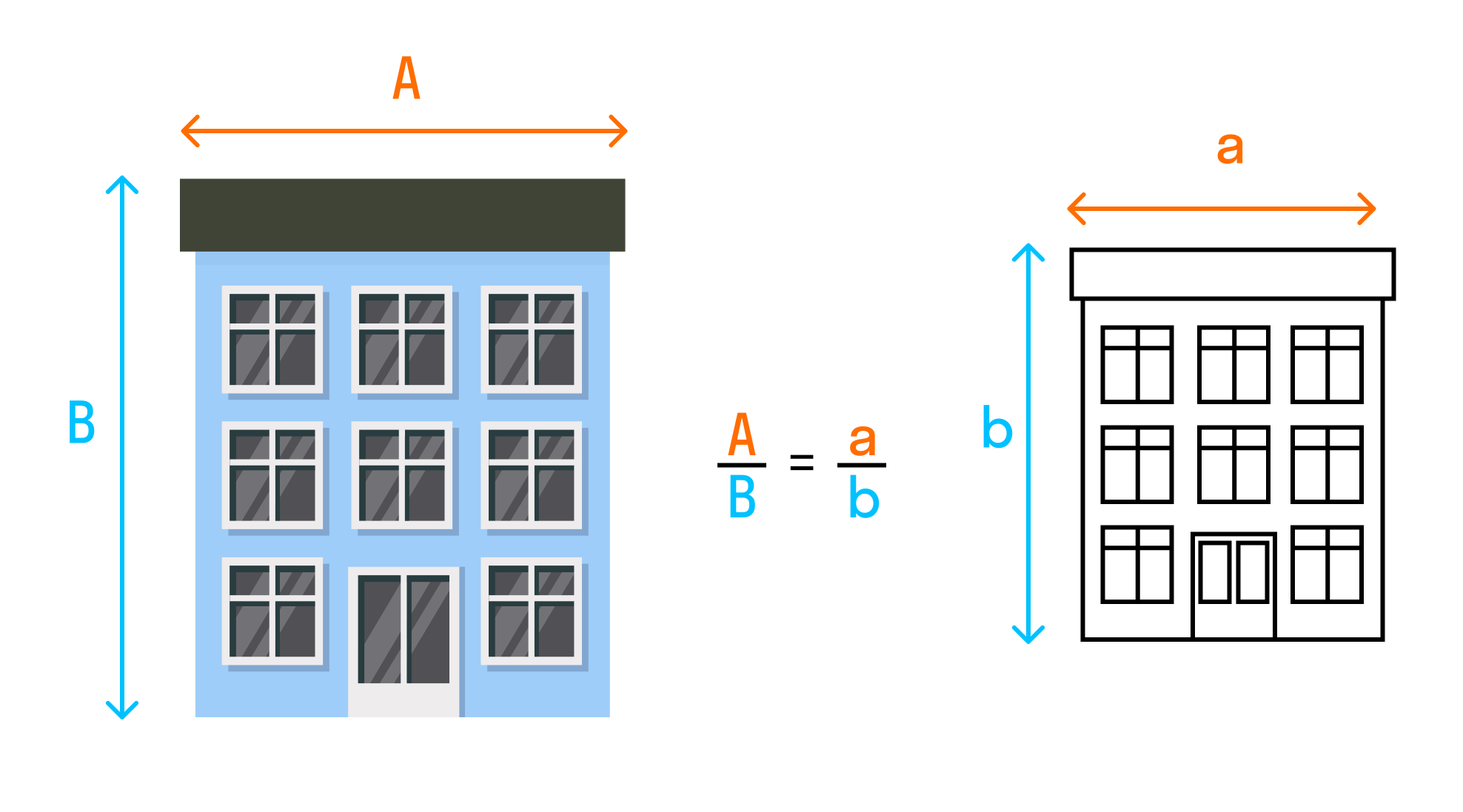
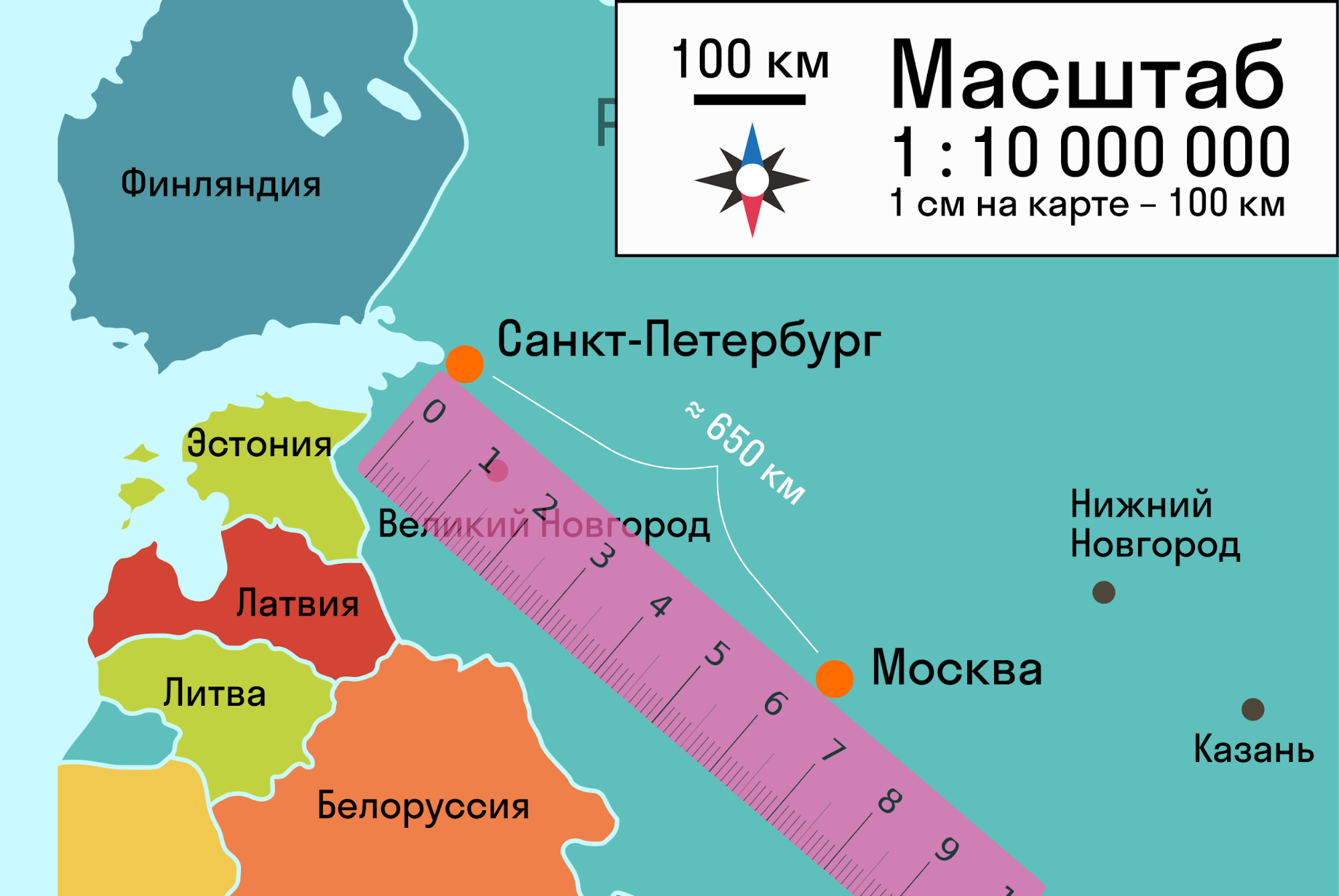
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.

Классификация треугольников по их сторонам

Для классификации треугольников можно использовать их типологию.

Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.

Свойства прямоугольного треугольника

С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.

Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.

Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.

Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.

От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃

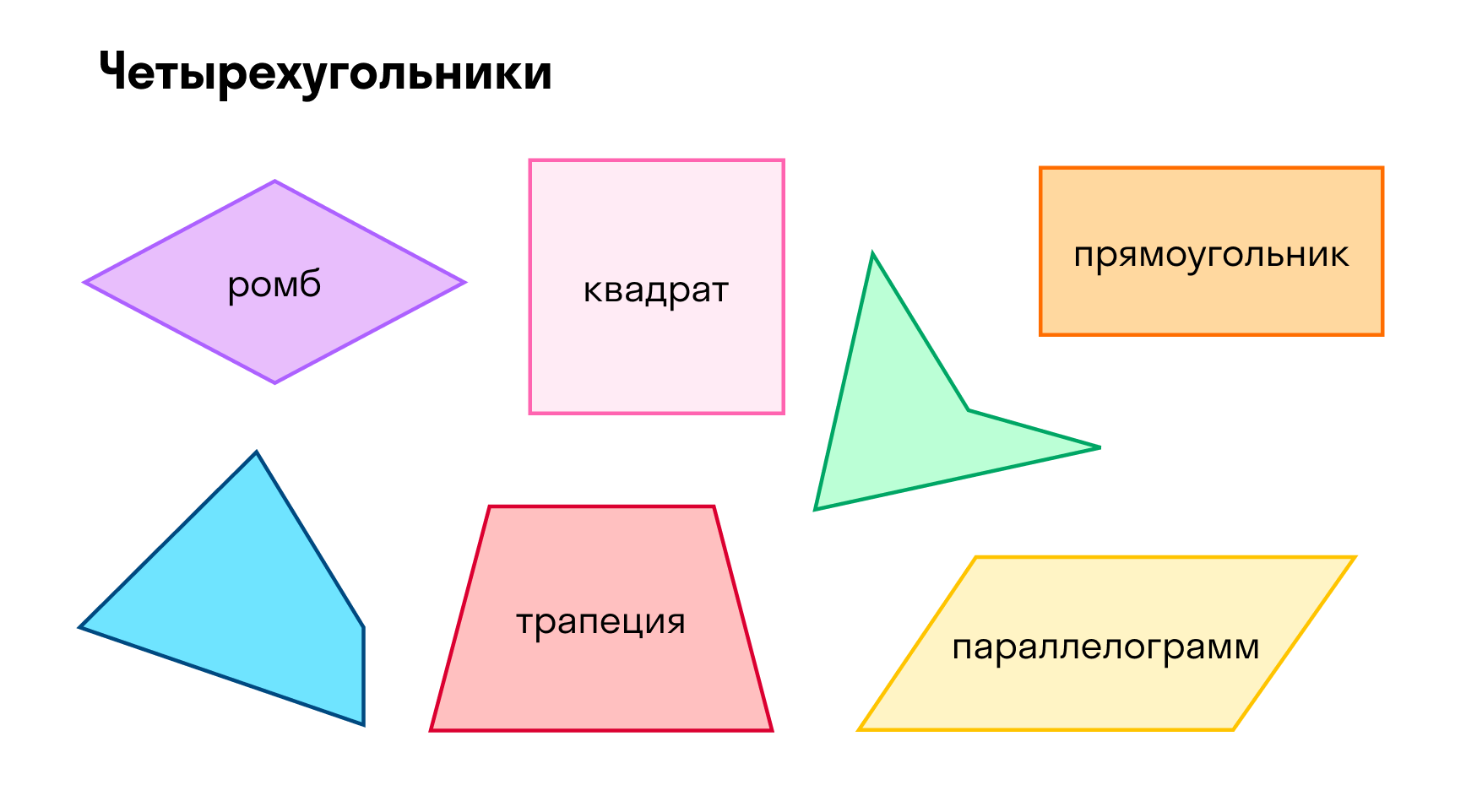
Четырехугольники

Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.

Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.

Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:

Окружность

Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.

Взаимодействие объектов

Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.

Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.

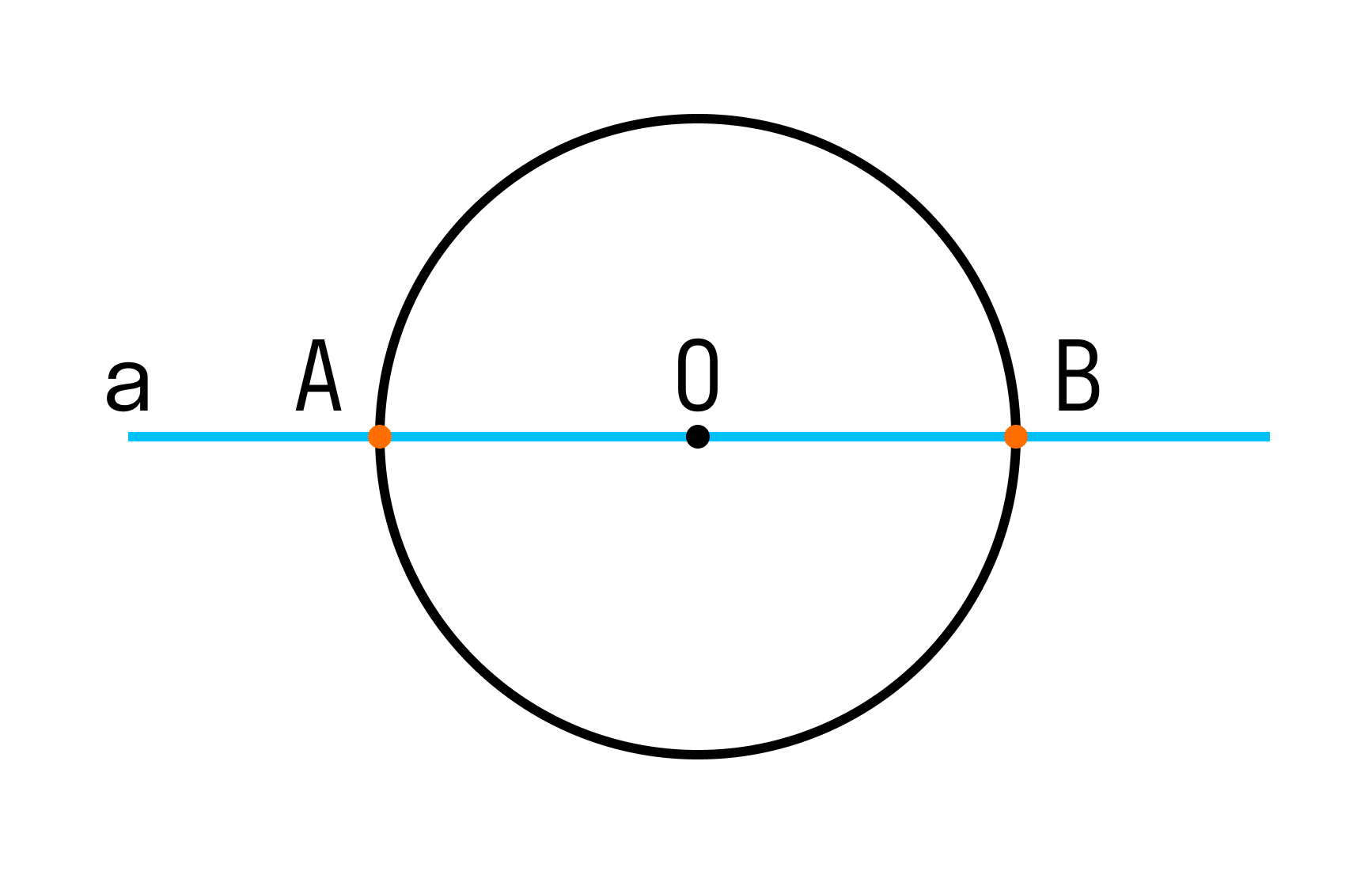
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.

На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.

Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:

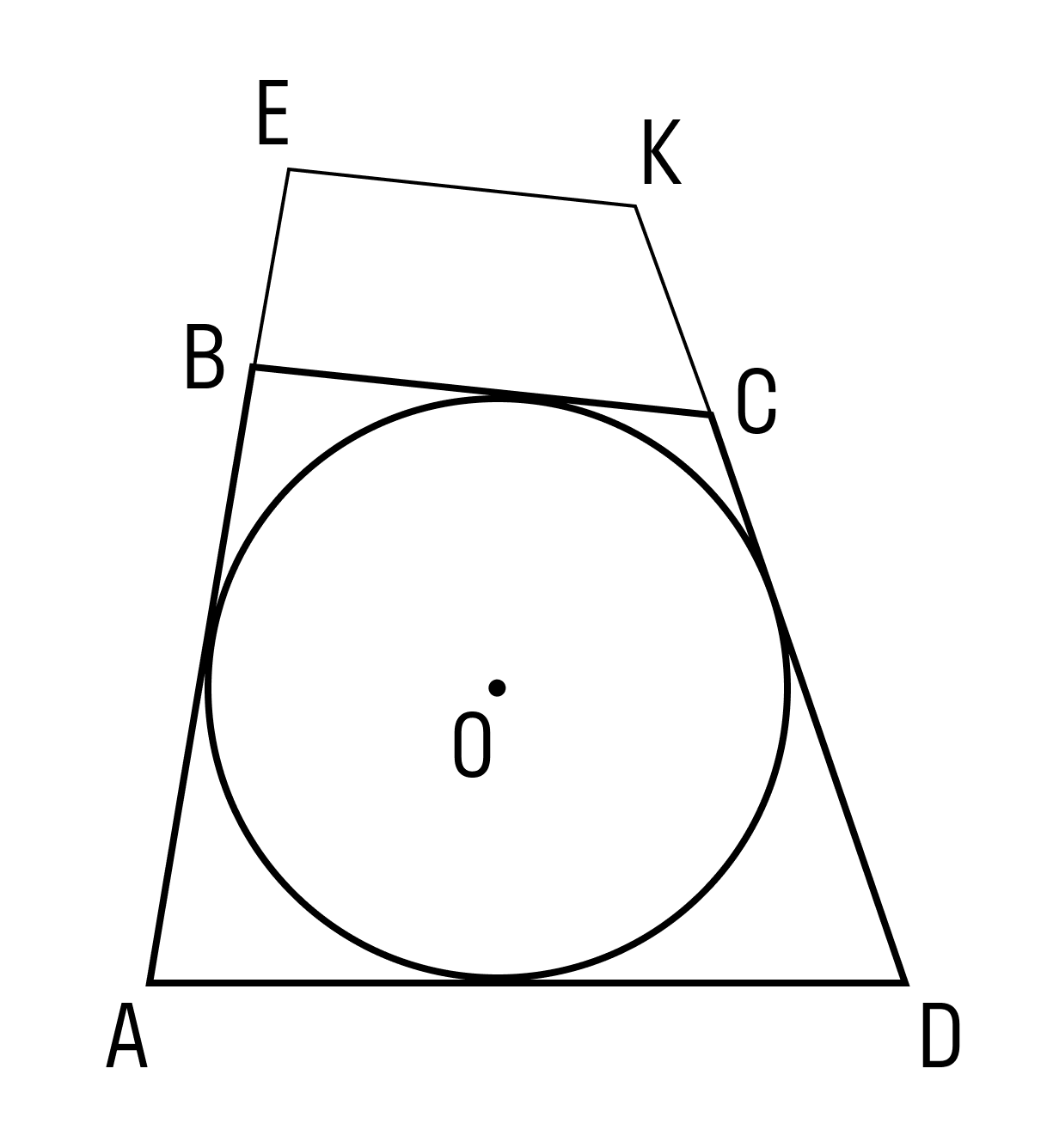
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.

На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.

В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.

Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.

Практическая сторона геометрии

Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.

Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.

А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.

Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.

Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.

Почему изучать геометрию сложно: некоторые правила придется учить наизусть.

Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.

Источник