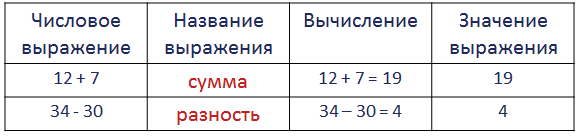
Что называют значением числового выражения привести

Числовые и буквенные выражения

Числовые выражения

В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.

Значение выражения — это результат выполненных действий.

Чтение числовых выражений

Решение числовых выражений

45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13

Сравнение значений числовых выражений

Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.

Для этого найдем значения каждого из них:

Буквенные выражения

Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.

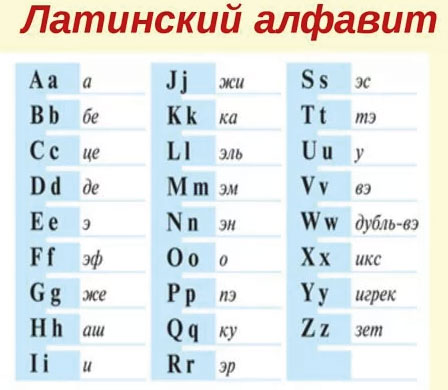
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.

Чаще всего используются буквы:

a, b, c, d, x, y, k, m, n

Алгоритм решения буквенного выражения

1. Прочитать буквенное выражение

2. Записать буквенное выражение

3. Подставить значение неизвестного в выражении

4. Вычислить результат

Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с

Подставим вместо неизвестного «с» число 4.

У нас получается выражение: 28 – 4

Переменные

Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.

Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства

Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:

Теперь мы можем найти значение этого выражения:

с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7

Поделись с друзьями в социальных сетях:

Источник

Значение числового, буквенного выражения и выражения с переменными

В процессе разбора тем о числовых, буквенных выражениях и выражениях с переменными следует обратить внимание на понятие значение выражения. Ниже дадим определение этому термину, рассмотрим примеры.

Что такое значение числового выражения

Мы знакомимся с числовыми выражениями с самого начала школьного обучения. Да и почти сразу начинает использоваться понятие «значение числового выражения». Так обозначают выражения, составляющие которого – числа, соединяемые знаками арифметических действий: плюс, минус, умножить, разделить.

Значение числового выражения – это конечное число, получаемое в результате выполнения заданных действий в исходном числовом выражении.

Зачастую в словосочетании «значение числового выражения» слово «числовое» не употребляют, поскольку в любом случае понятно, значение какого выражения рассматривается.

В основном интерес вызывает не само числовое выражение, а его значение. Практически всегда существует задача по нахождению значения заданного выражения, которая так и обозначается: «найти значение выражения». В соответствующей статье можно детально изучить сам процесс нахождения значения числовых выражения разного рода с примерами.

Значение буквенного выражения и выражения с переменными

Кроме числовых, интерес представляют и буквенные выражения – те выражения, составляющими которого являются, в том числе, одна или несколько букв. Буквы в буквенном выражении обозначают разные числа, и при замене букв на числа получается числовое выражение.

Значения букв – числа, которые заменяют эти буквы в буквенном выражении. Тогда значение буквенного выражения при заданных значениях букв – это значение полученного числового выражения.

Таким образом, речь идет не о значении буквенного выражения, как такового, а о его значении, когда заданы (определены) конкретные значения букв.

В программе алгебры буквы в буквенном выражении могут принимать разнообразные значения, тогда буквы называют переменными, а буквенные выражения – выражениями с переменными. Логично следует введение понятия значения выражений при выбранных значениях переменных.

Значение выражения с переменными при выбранных значениях переменных – это значение числового выражения, полученное при подстановке конкретных выбранных значений переменных в заданное выражение.

Возможен вариант, когда выбранные переменные –различны, а значение исходного выражения при этих переменных одинаково.

Значения переменных возможно задать из областей допустимых значений, которые им соответствуют, поскольку в ином случае, подставив значения, не принадлежащие области допустимых значений, можно получить числовое выражение, не имеющее смысла.

Источник

Значение числового, буквенного выражения и выражения с переменными.

При изучении темы числовые, буквенные выражения и выражения с переменными необходимо уделить внимание понятию значение выражения. В этой статье мы ответим на вопрос, что такое значение числового выражения, и что называют значением буквенного выражения и выражения с переменными при выбранных значениях переменных. Для разъяснения этих определений приведем примеры.

Навигация по странице.

Что называют значением числового выражения?

Знакомство с числовыми выражениями начинается чуть ли не с первых уроков математики в школе. Практически сразу вводится и понятие «значение числового выражения». Его относят к выражениям, составленным из чисел, соединенных знаками арифметических действий (+, −, ·, :). Дадим соответствующее определение.

Значение числового выражения – это число, которое получается после выполнения всех действий в исходном числовом выражении.

Часто в словосочетании «значение числового выражения» слово «числового» опускают, и говорят просто «значение выражения», так как все равно понятно, о значении какого выражения идет речь.

Часто на практике интерес представляет не столько числовое выражение, как его значение. То есть, встает задача, заключающаяся в определении значения данного выражения. При этом обычно говорят, что нужно найти значение выражения. В указанной статье подробно разобран процесс нахождения значения числовых выражений различного вида, и рассмотрена масса примеров с детальными описаниями решений.

Значение буквенного выражения и выражения с переменными

Помимо числовых выражений изучают буквенные выражения, то есть выражения, в записи которых вместе с числами присутствует одна или несколько букв. Буквы в буквенном выражении могут обозначать различные числа, и если буквы заменить этими числами, то буквенное выражение станет числовым.

Числа, которыми заменяют буквы в буквенном выражении, называют значениями этих букв, а значение полученного при этом числового выражения называют значением буквенного выражения при данных значениях букв.

Итак, для буквенных выражений говорят не просто о значении буквенного выражения, а о значении буквенного выражения при данных (заданных, указанных и т.п.) значениях букв.

В старших классах при изучении алгебры буквам в буквенных выражениях позволяют принимать различные значения, такие буквы называют переменными, а буквенные выражения – выражениями с переменными. Для этих выражений вводится понятие значения выражения с переменными при выбранных значениях переменных. Разберемся, что это такое.

Значением выражения с переменными при выбранных значениях переменных называется значение числового выражения, которое получается после подстановки выбранных значений переменных в исходное выражение.

Остается лишь добавить, что существуют выражения с переменными, значения которых не зависят от значений входящих в них переменных. Например, значение выражения с переменной x вида 2+x−x не зависит от значения этой переменной, оно равно 2 при любом выбранном значении переменной x из области ее допустимых значений, которая в данном случае является множеством всех действительных чисел.

Источник

Числовые и буквенные выражения

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Числовые выражения: что это

Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.

Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.

Например:

Это простые числовые выражения.

Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:

Это сложные числовые выражения.

Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».

Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.

Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.

11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.

При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:

Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)

Часто бывает нужно сравнить два числовых выражения.

Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.

Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2

14 больше 4
14 > 4
6 + 8 > 2 * 2

Буквенные выражения

Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.

В буквенном выражение есть цифры, знаки арифметических действия и буквы.

Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.

Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.

У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:

Пример 1. Найдите значение выражения: 5 + x.

Пример 2. Найдите значение выражения: (4 + a) * (2 + x).

Выражения с переменными

Переменная — это значение буквы в буквенном выражении.

Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.

Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.

5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a

Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.

Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.

Задание раз.

Задание два.

Составьте буквенное выражение:

Сумма разности b и 345 и суммы 180 и x.

Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.

Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?

150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.

Ответ: Маша и Лена посмотрели всего 313 видео.

Источник

Нахождение значения выражения: правила, примеры, решения

В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.

Как найти значение числового выражения?

Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.

Простейшие случаи

Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами.

Пример 1. Значение числового выражения

Выполним сначала умножение и деление. Получаем:

Теперь проводим вычитание и получаем окончательный результат:

Сначала выполняем преобразование дробей, деление и умножение:

Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:

Искомое значение найдено.

Выражения со скобками

Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.

Пример 3. Значение числового выражения

Значение выражений, содержащих скобки в скобках, находится по такому же принципу.

Пример 4. Значение числового выражения

Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним.

Выражения с корнями

Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.

Пример 5. Значение числового выражения

Сначала вычисляем подкоренные выражения.

Теперь можно вычислить значение всего выражения.

Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.

Пример 6. Значение числового выражения

Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.

Выражения со степенями

Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.

Пример 7. Значение числового выражения

Начинаем вычислять по порядку.

Осталось только провести операцию сложение и узнать значение выражения:

Также часто целесообразно бывает провести упрощение выражения с использованием свойств степени.

Пример 8. Значение числового выражения

Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.

Выражения с дробями

Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения.

Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.

Пример 9. Значение числового выражения

Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.

Перепишем наше выражение и вычислим его значение:

Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.

Пример 10. Значение числового выражения

Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.

Исходное выражение принимает вид:

Вычислим значение этого выражения:

Выражения с логарифмами

Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.

Пример 11. Значение числового выражения

По свойству логарифмов:

Вновь применяя свойства логарифмов, для последней дроби в выражении получим:

Теперь можно переходить к вычислению значения исходного выражения.

Выражения с тригонометрическими функциями

Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.

Пример 12. Значение числового выражения

Сначала вычисляем значения тригонометрических функций, входящих в выражение.

Подставляем значения в выражение и вычисляем его значение:

Значение выражения найдено.

Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.

Пример 13. Значение числового выражения

Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.

Общий случай числового выражения

В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.

Как найти значение выражения

Пример 14. Значение числового выражения

Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?

Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение.

π 6 + 2 · 2 π 5 + 3 π 5 = π 6 + 2 · 2 π + 3 π 5 = π 6 + 2 · 5 π 5 = π 6 + 2 π

Теперь можно узнать значение синуса:

Вычисляем значение подкоренного выражения:

2 · sin π 6 + 2 · 2 π 5 + 3 π 5 + 3 = 2 · 1 2 + 3 = 4

Со знаменателем дроби все проще:

Теперь мы можем записать значение всей дроби:

С учетом этого, запишем все выражение:

В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.

Вычисление значений выражений рациональными способами

Нахождение значений выражений с переменными

Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.

Нахождение значений выражений с переменными

Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.

Подставляем значения переменных в выражение и вычисляем:

Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.

Еще один пример. Значение выражения x x равно единице для всех положительных иксов.

Источник