Что называют высотой треугольника кратко

Высота треугольника

Высота треугольника — перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника

Содержание

Свойства

(Для доказательства тождества следует воспользоваться формулами

В качестве точки E следует взять пересечение двух высот треугольника.)

Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:

Минимальная высота в треугольнике всегда проходит внутри этого треугольника.

Основные соотношения

где — площадь треугольника, — длина стороны треугольника, на которую опущена высота.

где — основание.

Теорема о высоте прямоугольного треугольника

Если высота длиной h, проведённая из вершины прямого угла, делит гипотенузу длиной c на отрезки m и n, соответствующие b и a, то верны следующие равенства:

Мнемоническое стихотворение

См. также

Ссылки

Полезное

Смотреть что такое «Высота треугольника» в других словарях:

ВЫСОТА — ВЫСОТА, высоты, мн. высоты, высот, жен. 1. только ед. Протяжение снизу вверх, вышина. Высота дома. Башня большой высоты. || (мн. только спец. научн.). Расстояние от земной поверхности, измеряемое по вертикальной линии снизу вверх. Аэроплан летал… … Толковый словарь Ушакова

Высота (геометрия) — У этого термина существуют и другие значения, см. Высота (значения). Высота в элементарной геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на… … Википедия

высота — ы/; мн. высо/ты; ж. см. тж. высотка, высотный 1) Величина, протяжённость чего л. от нижней точки до верхней, снизу вверх. Высота/ дома, дерева, горы. Высота/ волны. Плотина высотой в сто пят … Словарь многих выражений

высота — ы; мн. высоты; ж. 1. Величина, протяжённость чего л. от нижней точки до верхней, снизу вверх. В. дома, дерева, горы. В. волны. Плотина высотой в сто пятьдесят метров. Измерить, определить высоту чего л. 2. Расстояние от какой л. поверхности до… … Энциклопедический словарь

высота исходного треугольника резьбы — (H) Расстояние между вершиной и основанием исходного треугольника резьбы в направлении, перпендикулярном к оси резьбы. [ГОСТ 11708 82 (СТ СЭВ 2631 80)] Тематики нормы взаимозаменяемости Обобщающие термины основные элементы и параметры резьбы EN… … Справочник технического переводчика

Высота (значения) — Высота размер или расстояние в вертикальном направлении. Другие значения: В астрономии: Высота светила угол между плоскостью математического горизонта и направлением на светило. В военном деле: Высота возвышенность рельефа. В… … Википедия

ВЫСОТА (в геометрии) — ВЫСОТА, в геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (напр., треугольника, пирамиды, конуса) на ее основание (или продолжение основания), а также длина этого отрезка. Высота призмы, цилиндра, шарового слоя, а… … Энциклопедический словарь

ВЫСОТА — в геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (напр., треугольника, пирамиды, конуса) на ее основание (или продолжение основания), а также длина этого отрезка. Высота призмы, цилиндра, шарового слоя, а также… … Большой Энциклопедический словарь

ВЫСОТА — ВЫСОТА, ы, мн. оты, от, отам, жен. 1. Величина, протяжённость чего н. от нижней точки до верхней. В. кирпичной кладки. В. прибоя. В. циклона. 2. Пространство, расстояние от земли вверх. Смотреть в высоту. Самолёт набирает высоту. Лететь на… … Толковый словарь Ожегова

Высота (геометрич.) — Высота в геометрии, отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или продолжение основания, а также длина этого отрезка. В. призмы, цилиндра, шарового слоя,… … Большая советская энциклопедия

Источник

Определение и свойства высоты треугольника

В данной публикации мы рассмотрим определение высоты треугольника, продемонстрируем, как она выглядит в зависимости от вида треугольника, а также перечислим ее основные свойства.

Определение высоты треугольника

Высота треугольника – это перпендикуляр, который опущен из вершины фигуры на противоположную сторону.

Основание высоты – точка на противоположной стороне треугольника, которую пересекает высота (или точка пересечения их продолжений).

Обычно высота обозначается буквой h (иногда как h_a – это означает, что она проведена к стороне a).

Высота в разных видах треугольников

В зависимости от вида фигуры высота может:

Свойства высоты треугольника

Свойство 1

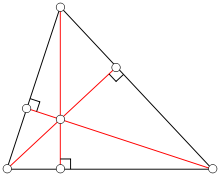
Все три высоты в треугольнике (или их продолжения) пересекаются в одной точке, которая называется ортоцентром (точка O на чертежах ниже).

Свойство 2

При пересечении двух высот в треугольнике, образуются следующие подобные треугольники:

Свойство 3

Точка пересечения высот в остроугольном треугольнике является центром окружности, вписанной в его ортотреугольник.

Ортотреугольник – треугольник, вершинами которого являются основания высот △ABC. В нашем случае – это △DEF.

Свойство 4

Точки, которые симметричны ортоцентру треугольника относительно его сторон, лежат на окружности, описанной вокруг этого треугольника.

Примечание: формулы для нахождения высоты треугольника подробно рассмотрены в нашей публикации – “Как найти высоту в треугольнике abc”.

Источник

Треугольник. Высота треугольника.

Высота треугольника – перпендикуляр, прочерченный из выбранной вершины треугольника на противолежащею его сторону. Для обозначения высоты треугольника используют букву h, к ней добавляется название той стороны, к которой она прочерчена: h_a, h_b, h_c,

Сторону треугольника, к которой прочерчена высота, называют основанием треугольника.

Высота треугольника может быть прочерчена к любой из трех сторон треугольника. Случается высота треугольника пересекает не само основание треугольника, а его продолжение. Так, высоты AD и ЕМ пересекают продолжения оснований ВС и FK.

Характерные особенности высоты.

В прямоугольном треугольнике высота, прочерченная из вершины прямого угла, разделит его на два треугольника, подобные первоначальному.

В остроугольном треугольнике две его высоты отделяют от него подобные треугольники.

Если треугольник остроугольный, то все основания высот принадлежат его сторонам, а у тупоугольного треугольника две высоты принадлежат продолжению сторон.

Три высоты в остроугольном треугольнике перекрещиваются в одной точке и эту точку обозначают как ортоцентр треугольника.

Источник

Высоты треугольника / Треугольники / Справочник по геометрии 7-9 класс

Высота треугольника. Свойство высоты прямоугольного треугольника

Для высоты прямоугольного треугольника, проведённой из вершины прямого угла, справедливо следующее утверждение.

Высоты можно провести из каждой вершины треугольника, однако у треугольников различных типов высоты располагаются по-разному, как показано в следующей таблице.

Видео

Формулы равнобедренного треугольника

Формулы сторон равнобедренного треугольника

b — основание равнобедренного треугольника

a — равные стороны равнобедренного треугольника

α — углы при основании

β — угол, образованный равными сторонами

Формулы длины стороны (основания b) равнобедренного треугольника

Формулы длины равных сторон равнобедренного треугольника (стороны a):

Формулы высоты, медианы, биссектрисы равнобедренного треугольника

b — основание равнобедренного треугольника

a — равные стороны равнобедренного треугольника

α — углы при основании

β — угол, образованный равными сторонами

L — высота, биссектриса и медиана

Формулы высоты, биссектрисы и медианы равнобедренного треугольника, через сторону и угол (L)

Формула высоты, биссектрисы и медианы равнобедренного треугольника, через стороны (L)

В треугольнике проведено две высоты

Первый «неожиданный факт»:

Почему бы это? Да очень просто! У них общий угол \( \displaystyle B\) и оба – прямоугольные. Значит, подобны по двум углам.

Второй «неожиданный» факт:

Здесь тоже подобие по двум углам: \( \angle 1=\angle 2\) (как вертикальные) и по прямому углу.

Третий, по-настоящему неожиданный факт:

\( \Delta ABC\sim \Delta <_>B<_>\)

Вот это уже интереснее, правда? Давай разбираться, почему так.

Остроугольный треугольник и высота

Вернёмся–ка к остроугольному треугольнику. Отметим на рисунке равные углы:

Что видим теперь? Ещё подобные треугольники!

Как от двух линий вообще могут получиться столько подобных треугольников?!

Видишь, какое богатство? И всё это может быть использовано в задачах!

Ну вот, теперь ты узнал что-то новенькое про высоты треугольника.

Теперь пробуй применять в задачах всё это – и соображение о том, что высота образует прямоугольный треугольник, и простые подобия прямоугольных треугольников, получающихся при пересечении двух высот, и подобие похитрее — которое с косинусом, и то, что угол между высотами равен углу между сторонами…

Главное, ты не старался просто запоминать все эти факты, а осознай, что их можно очень просто вывести.

И тогда, если ты будешь точно знать, например, что две проведённые высоты приносят кучу бонусов в виде всяких подобий, то ты непременно и сам получишь все эти бонусы, а заодно – решение своей задачи!

Свойства высоты в равностороннем треугольнике

Равносторонний треугольник — это треугольник, стороны которого, углы, высоты, медианы, оси симметрии и биссектрисы будут равны.

Такой треугольник является частным примером равнобедренного треугольника, но не наоборот.

Высоту в таком треугольнике можно найти с помощью следующей формулы:

h=a32 где а — сторона равностороннего треугольника.

Главным свойством, которым обладает высота равностороннего треугольника, является тот факт, что она равна медиане и биссектрисе:

а — сторона правильного равностороннего треугольника.

Что мы узнали?

Мы узнали, что такое высота треугольника, какие бывают высоты и как они обозначаются. Разобрались в типовых задачах и записали три формулы для высоты треугольника.

В отличие от медианы или биссектрисы, высота треугольника может быть расположена как внутри треугольника, так и вне его.

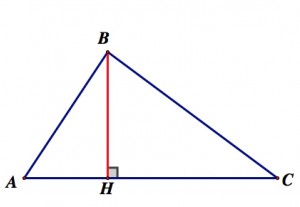
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону.

На рисунке BF — высота, проведенная из вершины B к стороне AC.

Все три высоты треугольника пересекаются в одной точке. Эта точка называется ортоцентром треугольника.

Высоты остроугольного треугольника расположены строго внутри треугольника.

Соответственно, точка пересечения высот также находится внутри треугольника.

В прямоугольном треугольнике две высоты совпадают со сторонами. (Это высоты, проведенные из вершин острых углов к катетам).

Высота, проведенная к гипотенузе, лежит внутри треугольника (позднее рассмотрим ее свойства).

AC — высота, проведенная из вершины С к стороне AB.

AB — высота, проведенная из вершины B к стороне AC.

AK — высота, проведенная из вершины прямого угла А к гипотенузе ВС.

Высоты прямоугольного треугольника пересекаются в вершине прямого угла (А — ортоцентр).

В тупоугольном треугольника внутри треугольника лежит только одна высота — та, которая проведена из вершины тупого угла.

Две другие высоты лежат вне треугольника и опущены к продолжению сторон треугольника.

AK — высота, проведенная к стороне BC.

BF — высота, проведенная к продолжению стороны АС.

CD — высота, проведенная к продолжению стороны AB.

Точка пересечения высот тупоугольного треугольника также находится вне треугольника:

Источник

Элементы треугольника. Высоты

Определение

Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника.

Свойства

1. Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон

2. Высоты треугольника (или их продолжения) пересекаются в одной точке, называемой ортоцентром

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному

4. В остроугольном треугольнике две его высоты отсекают от него подобные треугольники

Некоторые формулы, связанные с высотой треугольника

где — площадь треугольника, — длина стороны треугольника, на которую опущена высота

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник