Что называют высотой параллелограмма кратко
Высота параллелограмма
Что такое высота параллелограмма? Сколько у параллелограмма высот?
Что такое основание параллелограмма?
Высота параллелограмма — это перпендикуляр, опущенный из любой точки одной стороны параллелограмма на прямую, содержащую противоположную сторону.
Высотой параллелограмма также называют длину этого перпендикуляра. Расстояние между противоположными сторонами параллелограмма равно высоте параллелограмма.
BK, PF, DE — высоты параллелограмма.
BK, PF, DE — меньшие высоты параллелограмма.
Меньшая высота параллелограмма — это высота, проведенная к его большей стороне.
BM, DL — высоты параллелограмма.
BM, DL — большие высоты параллелограмма.
Большая высота высота параллелограмма — это высота, проведенная к ее меньшей стороне.
На рисунке 3 BK и BM — высоты параллелограмма ABCD, проведенные из вершины тупого угла B.
Из них BM — большая высота параллелограмма ABCD, BK — его меньшая высота.
На рисунке 4 CN и CH — высоты, проведенные из вершины острого угла C параллелограмма ABCD.
Из них CN — меньшая высота, CH- большая высота параллелограмма.
Иногда одну из сторон называют основанием параллелограмма.
Например, на рисунке 3 AD — основание параллелограмма, BK — проведенная к нему высота.
CD тоже можно считать основанием параллелограмма. BM — проведенная к нему высота.
Но чаще об основании говорят, когда хотят подчеркнуть, что эта сторона — нижняя горизонтальная (для понимания того, как лучше выполнить рисунок).
Параллелограмм
Параллелограмм — это четырёхугольник, у которого противоположные стороны параллельны. Если у параллелограмма все углы прямые, то такой параллелограмм называется прямоугольником, а прямоугольник, у которого все стороны равны, называется квадратом.
Все параллелограммы обладают следующими свойствами:
Точка O — это центр симметрии.
Высота
Нижняя сторона параллелограмма называется его основанием, а перпендикуляр, опущенный на основание из любой точки противоположной стороны, — высотой.
AD — это основание параллелограмма, h — высота.
Высота выражает расстояние между противоположными сторонами, поэтому определение высоты можно сформулировать ещё так: высота параллелограмма — это перпендикуляр, опущенный из любой точки одной стороны на противоположную ей сторону.
Площадь
Для измерения площади параллелограмма можно представить его в виде прямоугольника. Рассмотрим параллелограмм ABCD:
Построенные высоты BE и CF образуют прямоугольник EBCF и два треугольника: ΔABE и ΔDCF. Параллелограмм ABCD состоит из четырёхугольника EBCD и треугольника ABE, прямоугольник EBCF состоит из того же четырёхугольника и треугольника DCF. Треугольники ABE и DCF равны (по четвёртому признаку равенства прямоугольных треугольников), значит и площади прямоугольника с параллелограммом равны, так как они составлены из равных частей.
Итак, параллелограмм можно представить в виде прямоугольника, имеющего такое же основание и высоту. А так как для нахождения площади прямоугольника перемножаются длины основания и высоты, значит и для нахождения площади параллелограмма нужно поступить также:
Из данного примера можно сделать вывод, что площадь параллелограмма равна произведению его основания на высоту.
Общая формула площади параллелограмма:
где S — это площадь параллелограмма, a — основание, h — высота.
Висота паралелограма дорівнює співвідношенню площі до підстави (Формула 1)
Висота паралелограма дорівнює твору бічної сторони на синус кута при його основі (Формула 2)
Співвідношення підстав паралелограма дорівнює обернено пропорційному співвідношенню висот, опущених на відповідні сторони (Формула 3)
Висоти паралелограма, опущені з однієї вершини, утворюють кут, рівний куту паралелограма при сусідній вершині (Малюнок 2)
Висота паралелограма рівна, корню з різниці квадрата бічної сторони і квадрата довжини відрізка, створюючого прямокутний трикутник, іншими сторонами якого є бічна сторона і висота (Формула 4)
Висота паралелограма дорівнює корню з різниці квадрата діагоналі, з якої опущена висота і квадрата довжини відрізка між точкою, з якої проведена діагональ і точкою пересічення висоти і основання (Формула 5)
Задача
| Висота паралелограма проведена з вершини тупого кута і дорівнює 5 см. Висота ділить сторону парелелограма навпіл. Гострий кут паралелограма доривнюе 30 градусів. Знайдіть діагональ паралелограма, проведену з вершини тупого кута, и кути, яки вона утворює зі сторонами паралелограма. | Высота параллелограмма проведена из вершины тупого угла и равняется 5 см. Высота делит сторону параллелограмма пополам. Острый угол равняется 30 градусам. Найдите диагональ параллелограмма, проведенную из вершины тупого угла и углы, которые она образует со сторонами параллелограмма. |
Найдем длину диагонали.
BE / BD = cos ∠EBD
BE / BD = cos 60
Подставим значение косинуса 60 градусов и получим:
BE / BD = 1/2
По условию задачи BE = 5 см, откуда
5 / BD = 1/2
BD = 10
Ответ: длина диагонали параллелограмма равна 10 см, углы, которые образует диагональ с основаниями равны 30 и 120 градусов.
Параллелограмм: свойства и признаки
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
Как найти площадь параллелограмма:
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Параллелограмм. Свойства и признаки параллелограмма
Определение параллелограмма
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма
1. Противоположные стороны параллелограмма попарно равны
2. Противоположные углы параллелограмма попарно равны
3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов
4. Сумма всех углов равна 360°
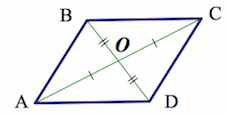
6. Точка пересечения диагоналей является центром симметрии параллелограмма
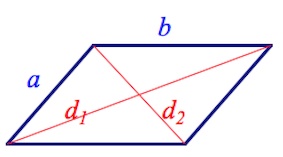
7. Диагонали параллелограмма и стороны
связаны следующим соотношением:
8. Биссектриса отсекает от параллелограмма равнобедренный треугольник
Признаки параллелограмма
Четырехугольник является параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Противоположные стороны попарно равны:
2. Противоположные углы попарно равны:
3. Диагонали пересекаются и в точке пересечения делятся пополам
4. Противоположные стороны равны и параллельны:
5.
Небольшой видеоролик о свойствах параллелограмма (в том числе ромба, прямоугольника, квадрата) и о том, как эти свойства применяются в задачах:
 Формулы площади параллелограмма смотрите здесь.
Формулы площади параллелограмма смотрите здесь.Хорошую подборку задач на нахождение углов и длин в параллелограмме смотрите здесь.