Что называют векторной величиной
Что такое векторные величины в физике? Все векторные величины
Содержание:
Физические величины служат для численного выражения различных характеристик материальных предметов и физических явлений. Все физические величины разделены на два вида. Векторные величины в физике – это те, которые кроме численного выражения обязательно характеризуются направлением. А вот обычные величины называют скалярными. Примерами таких величин могут служить:
Что такое векторная величина
Векторные величины в физике, список которых приведен ниже, широко известны:
Чтобы досконально разобраться в их смысле, попробуем рассмотреть простой пример. Каждый из нас неоднократно бросал или подбрасывал какой-либо предмет. Пусть это будет теннисный мячик. Сделать это можно разными способами:
В нашем эксперименте будем предполагать, что все три раза мячик бросает один и тот же человек, а сила броска всегда примерно одинакова. Какие результаты будут в итоге? Догадаться довольно просто: в каждом из случаев результат будет разным, потому что три раза мячик бросали в разном направлении. Таким образом мы увидели, что векторная величина это в физике одновременно две характеристики какого-либо физического процесса или состояния.
Действия над векторными величинами
Теперь, когда мы установили, что такое векторная величина в физике, настало время подумать о действиях над такими величинами. Их можно складывать, вычитать, умножать, но важно помнить, что определяющим фактором будет их направление. Действия над такими величинами производят с использованием правил, принятых в математике. Например, сложение векторов производят с использованием правил треугольника или параллелограмма.
Что значит векторная величина в обычной жизни
В повседневной жизни мы зачастую даже не задумываемся, что значит векторная величина, и не замечем, что пользуемся векторами. Допустим, что два друга собрались поехать на рыбалку и договорились о встрече с утра за 100 м от автобусной остановки. Согласитесь, что намеченное мероприятие может оказаться под угрозой из-за того, что не было указано в каком конкретно направлении от остановки следует двигаться на указанное расстояние.
Другой пример из всем известной басни. Речь про лебедя, рака и щуку, которые дружно собрались потянуть тяжелый воз. Тяговую силу каждый из них приложил в своем направлении, не согласовав его с другими. В итоге воз не тронулся с места. Говоря языком физики, все векторные величины силы математически сложились так, что их равнодействующая оказалась равной нулю.
Ну и в заключительной части вспомним о том, что векторы в виде указующих стрелок принято использовать на дорожных знаках и различных табличках, информирующих о направлении движения в непредвиденных ситуациях либо помогающих найти соответствующий объект.
Что такое вектор и векторные величины? Какие их свойства, признаки?
Содержание:
Одни величины в физике называют скалярными, другие – векторными, и последним посвящён целый раздел алгебры. Кратко разберёмся, какие величины называют векторными, определим их свойства. Узнаем основные параметры этих отрезков, сферы применения, возможные манипуляции с ними.
Что такое векторная величина
Часто линия и сторона действия объединяются в направление вектора.
Очевидно, термин происходит из латинского языка: vector – несущий.
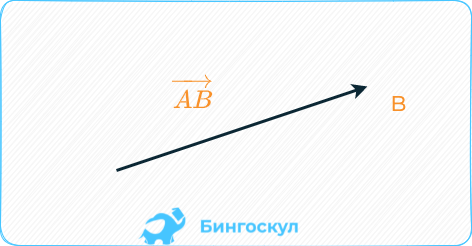
Обозначение
В последней ситуации первая буква указывает на начальную точку или начало направленного отрезка, вторая – на его конец. Их порядок указывает на направленность вектора. Отсюда следует, что порядок указания букв важен. AB ≠ BA как в случае с обычными отрезками. На чертежах направление изображают стрелкой на конце, начало представляют точкой. Длиной называется разница между конечной и начальной точками. Обозначается преимущественно буквой V со стрелкой/риской вверху \overrightarrow
Свойства и классификация векторов
Величины можно складывать – суммировать, отнимать – вычислять их разницу, умножать – находить произведение и определять длину (модуль). Причем операции производятся как с векторами, так и по отношению к направленному отрезку и числу.
Применение
Применение направленных отрезков упрощает определение меры углов между отрезками, лучами, прямыми, вычисление площадей геометрических фигур. В компьютерной графике векторы-нормали применяют для освещения сцен и создания масштабируемых изображений, качество которых не страдает при уменьшении или увеличении картинки. Рассматриваемые отрезки положены в основу системы полярных координат. Существует отдельный раздел компьютерной графики – векторный.
Скользящие «несущие» широко применяются в физике (механике), например, это сила. При перемещении вектора силы вдоль прямой, которой тот принадлежит, момент силы остаётся константой. При перемещении на иную прямую он зачастую меняется. Сила не рассматривается как свободный направленный отрезок.
Два вида физических величин: скалярные величины и векторные величины
«Что-то я не помню такой темы в физике» — первое, что, наверное, пришло вам в голову. Да, вы правы — тема незаметная, но в некоторых учебниках она присутствует. «А нужна она мне для ЕГЭ?» Нужна. Точно нужна. Очень нужна. Постоянно нужна.
Давайте приступим. Надо запомнить, что в физике (школьной) есть два типа физических величин:
Векторная величина. Что это такое? Давайте вспомним (а для тех, кто не знал — узнаем), что
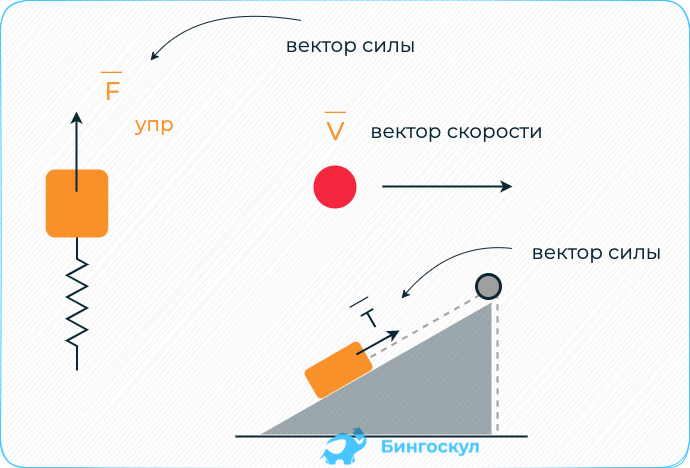
Направление вектора изображается на картинке. Куда показывает вектор — туда он и направлен. Например, бывает так, что вектор направлен вверх, вниз и т.д. Вектор может быть направлен вдоль какой-то плоскости. Примеры можете видеть на картинках.
Ну, самое простое — это опыт. Решая задачи, читая теоретический материал, вы со временем запомните, какие величины векторные, а какие скалярные. Физических величин не так много, как может показаться.
А способ чуть посложнее — это представить эти величины и решить для себя: могут они иметь направление? Если да — то это вектор, если нет — скаляр.
Например: заряд конденсатора. Если заряд имеет направление, то куда он направлен? Непонятно — поэтому, скорее всего, заряд — это скалярная величина.
Другой пример: длина отрезка. Если эта физическая величина имеет направление, то откуда куда она направлена: от точки 1 до точки 2? Или от точки 2 до точки 1? Трудно выбрать — поэтому, скорее всего, длина отрезка — это скаляр.
Какие из представленных на рисунках величин являются скалярными, а какие — векторными?
Векторная величина: из чего состоит и примеры
Содержание:
Авеличина вектора Это любое выражение, представленное вектором, имеющим числовое значение (модуль), направление, направление и точку приложения. Некоторые примеры векторных величин: смещение, скорость, сила и электрическое поле.
Векторная величина аналитически представлена буквой со стрелкой вверху, указывающей вправо в горизонтальном направлении. Он также может быть представлен буквой, выделенной жирным шрифтом. V модуль которого ǀVǀ написано курсивом В.
Что такое векторная величина?
Модуль: Это числовое значение, которое указывает размер или интенсивность величины вектора.
Адрес: Это ориентация линейного сегмента в пространстве, которое его содержит. Вектор может иметь горизонтальное, вертикальное или наклонное направление; север, юг, восток или запад; северо-восток, юго-восток, юго-запад или северо-запад.
Смысл: Обозначается стрелкой в конце вектора.
Точка приложения: Это начало или начальная точка вектора.
Классификация векторов
Векторы подразделяются на коллинеарные, параллельные, перпендикулярные, параллельные, компланарные, свободные, скользящие, противоположные, групповые, фиксированные и единичные.
Коллинеарный: Они принадлежат или действуют на одной прямой, их также называют линейно зависимый и они могут быть вертикальными, горизонтальными и наклонными.
Параллельный: Они имеют одинаковое направление или наклон.
Перпендикуляр: два вектора перпендикулярны друг другу, если угол между ними равен 90 °.
Одновременный: Это векторы, которые при скольжении по своей линии действия совпадают в одной и той же точке пространства.
Копланары: Они действуют в самолете, например в самолете ху.
Свободно: Они перемещаются в любой точке пространства, сохраняя свой модуль, направление и смысл.
Слайдеры: Они движутся по линии действия, определяемой их направлением.
Противоположности: У них одинаковый модуль и направление и противоположное направление.
Teamlenses: У них одинаковый модуль, направление и смысл.
Исправлена: У них неизменная точка применения.
Унитарный: Векторы, модулем которых является единица измерения.
Компоненты вектора
Векторная величина в трехмерном пространстве представлена в системе трех взаимно перпендикулярных осей (X и Z) называется ортогональным трехгранником.
На изображении векторы Vx, Vy, Vz компоненты вектора вектора V чьи единичные векторы Икс,Y,z. Величина вектора V представлен суммой его векторных компонентов.
Результат нескольких векторных величин является векторной суммой всех векторов и заменяет эти векторы в системе.
Векторное поле
Векторное поле графически представлено линиями поля, которые представляют собой касательные линии векторной величины во всех точках области. Некоторыми примерами векторных полей являются электрическое поле, создаваемое точечным электрическим зарядом в пространстве, и поле скорости жидкости.
Векторные операции
Скалярное произведение: Произведение скалярной величины к по величине вектора п это вектор mP который имеет то же направление вектора П. Если скалярная величина равна нулю, скалярное произведение представляет собой нулевой вектор.
Примеры векторных величин
Позиция
Ускорение
Среднее ускорение (км) определяется как изменение скорости v во временном интервале Δt и выражение для его вычисления км= Δv / Δt, будучи Δv вектор изменения скорости.
Гравитационное поле
Гравитационная сила притяжения, создаваемая массой M, расположенный в начале координат, на другой массе м в точке в космосе Икс, Y, z это векторное поле, называемое гравитационным силовым полем. Эта сила выражается выражением:
Ссылки
Амфетамины: характеристики и побочные эффекты
Могут ли животные страдать психическим заболеванием?
Векторная величина
В большинстве случаев термин вектор употребляется в физике для обозначения вектора в так называемом «физическом пространстве», т.е. в обычном трехмерном пространстве в классической физике или в четырехмерном [1] пространстве-времени в современной физике (в последнем случае понятие вектора и векторной величины совпадают с понятием 4-вектора и 4-векторной величины).
Употребление словосочетания «векторная величина» практически исчерпывается этим. Что же касается употребления термина «вектор», то оно, несмотря на тяготение по умолчанию к этому же полю применимости, в большом количестве случаев всё же весьма далеко выходит за такие рамки. Об этом см. ниже.
Содержание
Употребление терминов вектор и векторная величина в физике
В целом в физике понятие вектора практически полностью совпадает с таковым в математике. Однако есть терминологическая специфика, связанная с тем, что в современной математике это понятие несколько излишне абстрактно (по отношению к нуждам физики).
В математике, произнося «вектор» понимают скорее вектор вообще, т.е. любой вектор любого сколь угодно абстрактного линейного пространства любой размерности и природы, что, если не прилагать специальных усилий, может приводить даже к путанице (не столько, конечно, по существу, сколько по удобству словоупотребления). Если же необходимо конкретизировать, в математическом стиле приходится или говорить довольно длинно («вектор такого-то и такого-то пространства»), или иметь в виду подразумеваемое явно описанным контекстом.
В физике же практически всегда речь идет не о математических объектах (обладающих теми или иными формальными свойствами) вообще, а об определенной их конкретной («физической») привязке. Учитывая эти соображения конкретности с соображениями краткости и удобства, можно понять, что терминологическая практика в физике заметно отличается от математической. Однако она не входит с последней в явное противоречие. Этого удается достичь несколькими простыми «приемами». Прежде всего, к ним относится соглашение об употребление термина по умолчанию (когда контекст особо не оговаривается). Так, в физике, в отличие от математики, под словом вектор без дополнительных уточнений обычно понимается не «какой-то вектор любого линейного пространства вообще», а прежде всего вектор, связанный с «обычным физическим пространством» (трехмерным пространством классической физики или четырехмерным пространством-временем [2] физики релятивистской). Для векторов же пространств, не связанных прямо и непосредственно с «физическим пространством» или «пространством-временем», как раз применяют специальные названия (иногда включающие слово «вектор», но с уточнением). Если вектор некоторого пространства, не связанного прямо и непосредственно с «физическим пространством» или «пространством-временем» (и которое трудно сразу как-то определенно охарактеризовать), вводится в теории, он часто специально описывается как «абстрактный вектор».
Всё сказанное еще в большей степени, чем к термину «вектор», относится к термину «векторная величина». Умолчание в этом случае еще жестче подразумевает привязку к «обычному пространству» или пространству-времени, а употребление по отношению к элементам абстрактных векторных пространств скорее практически не встречается, по крайней мере, такое применение видится редчайшим исключением (если вообще не оговоркой).
Примеры векторных физических величин: скорость, сила, поток тепла.
Генезис векторных величин
Каким образом физические «векторные величины» привязаны к пространству? Прежде всего, бросается в глаза то, что размерность векторных величин (в том обычном смысле употребления этого термина, который разъяснен выше) совпадает с размерностью одного и того же «физического» (и «геометрического») пространатсва, например, пространство трехмерно и вектор электрического поля трехмерен. Интуитивно можно заметить также, что любая векторная физическая величина, какую бы туманную связь она не имела с обычной пространственной протяженностью, тем не менее имеет вполне определенное направление именно в этом обычном пространстве.
Эта процедура имеет две различные (хотя по сути детально повторяющие друг друга) реализации для трехмерного случая классической физики и для четырехмерной пространственно-временной формулировки, обычной для современной физики.
Классический трехмерный случай
Будем исходить из обычного трехмерного «геометрического» пространства, в котором мы живем и можем перемещаться.
В качестве исходного и образцового вектора возьмем вектор бесконечно малого перемещения. Довольно очевидно, что это обычный «геометрический» вектор (как и вектор конечного перемещения).
Также новый вектор дает дифференцирование вектора по скаляру (поскольку такая производная есть предел отношения разности векторов к скаляру). Это можно сказать дальше и о производных всех высших порядков. То же верно по отношению к интегрированию по скалярам (времени, объему).
Из скорости и ускорения, умножением на скаляр (массу), появляются
Поскольку нас сейчас интересуют и псевдовекторы, заметим, что
Продолжая эту процедуру, мы обнаруживаем, что все известные нам векторные величины оказываются теперь не только интуитивно, но и формально, привязаны к исходному пространству. А именно все они в некотором смысле являются его элементами, т.к. выражаются в сущности как линейные комбинации других векторов (со скалярными множителями, возможно, и размерными, но скалярными, а поэтому формально вполне законными).
Современный четырехмерный случай
Ту же процедуру можно проделать исходя из четырехмерного перемещения. Оказывается, что все 4-векторные величины «происходят» от 4-перемещения, являясь поэтому в некотором смысле такими же векторами пространства-времени, как и само 4-перемещение.