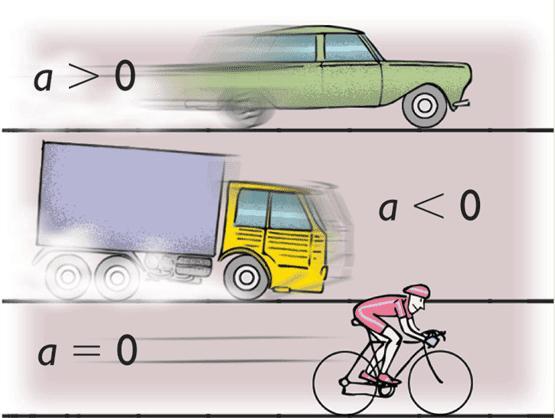
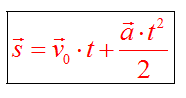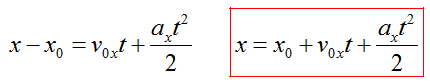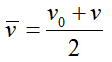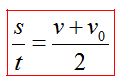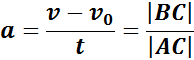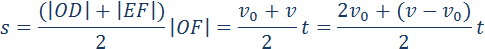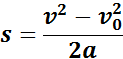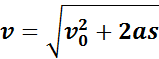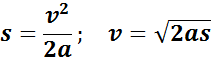Что называют ускорением равноускоренного движения

Ускорение. Равноускоренное движение

Что такое ускоренное движение

Ускоренное движение — что это такое? Хороший вопрос. Давайте разберем это понятие по словам.

«Движение» — значит, что-то двигается. Ага, значит тело перемещается, значит у него есть какая-то скорость.

«Ускоренное» — значит «убыстренное», с возрастающей скоростью, когда тело двигается все быстрее и быстрее. Ага, значит скорость не постоянная. Она меняется. Тело двигается все быстрее, быстрее и быстрее. То есть скорость все время увеличивается.

Чтобы быть конкретнее, посмотрим на пример: мальчик на велосипеде разгоняется из состояния покоя. Сначала у него скорость 5 5 5 км/ч, потом 1 0 10 1 0 км/ч, потом 1 5 15 1 5 км/ч, 2 0 20 2 0 км/ч, 2 5 25 2 5 км/ч, 3 0 30 3 0 км/ч и т.д. — насколько у него хватит сил.

Точно так же, как мальчик разгоняется на велосипеде, кто-то, например девочка на самокате, может тормозить, останавливаться, двигаться все медленнее, медленнее и медленнее. В конце — остановиться. Сначала у нее может быть скорость 1 0 10 1 0 км/ч, потом 5 5 5 км/ч, а потом 0 0 0 км/ч. То есть скорость все время уменьшается на 5 5 5 км/ч.

Вернемся к примеру с девочкой. Мы видим, что ее скорость начинает возрастать в отрицательном направлении. То есть наше замедленное движение девочки на самокате переходит в ускоренное движение (когда скорость набирается), но уже в противоположную сторону. Именно поэтому замедленное движение — это вариант ускоренного движения. Поэтому между ускоренным и замедленным движениями (как правило) не делают различий и называют их просто ускоренным движением.

В итоге мы пришли к тому, что ускоренное движение — это движение, при котором меняется скорость. Но мы помним, что скорость — это векторная величина. А любой вектор характеризуется двумя величинами: длиной и направлением. Так вот, оказывается, что тело движется с ускорением в случае, если меняется скорость по величине (тело убыстряет свое движение) или же тело меняет направление скорости (тело поворачивает). Первый случай (с изменением величины — или, как говорят, модуля) мы рассмотрим сейчас в теме «Равноускоренное движение», а второй случай — с поворотом — в теме «Движение по окружности», когда тело поворачивает, а значит — изменяет направление скорости.

Ускорение

— это очень полезная для нас формула. Ее нужно запомнить.

Источник

I. Механика

Тестирование онлайн

Равноускоренное движение

Физическая величина, характеризующая то, на сколько каждый раз увеличивается скорость называется ускорением.

Ускорение тела

Эту формулу чаще всего при решении задач применяют в видоизмененном виде:

Направление вектора ускорения

Направление вектора ускорения изображено на рисунках

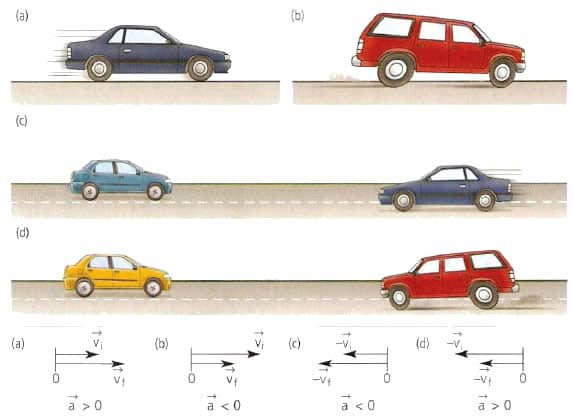
На этом рисунке машина движется в положительном направлении вдоль оси Ox, вектор скорости всегда совпадает с направлением движения (направлен вправо). Когда вектор ускорение совпадает с направлением скорости, это означает, что машина разгоняется. Ускорение положительное.

При разгоне направление ускорения совпадает с направлением скорости. Ускорение положительное.

На этом рисунке машина движется в положительном направлении по оси Ox, вектор скорости совпадает с направлением движения (направлен вправо), ускорение НЕ совпадает с направлением скорости, это означает, что машина тормозит. Ускорение отрицательное.

При торможении направление ускорения противоположно направлению скорости. Ускорение отрицательное.

Разберемся, почему при торможении ускорение отрицательное. Например, теплоход за первую секунду сбросил скорость с 9м/с до 7м/с, за вторую секунду до 5м/с, за третью до 3м/с. Скорость изменяется на «-2м/с». 3-5=-2; 5-7=-2; 7-9=-2м/с. Вот откуда появляется отрицательное значение ускорения.

При решении задач, если тело замедляется, ускорение в формулы подставляется со знаком «минус».

Перемещение при равноускоренном движении

Дополнительная формула, которую называют безвременной

Формула в координатах

Связь со средней скоростью

При равноускоренном движении среднюю скорость можно рассчитывать как среднеарифметическое начальной и конечной скорости

Из этого правила следует формула, которую очень удобно использовать при решении многих задач

Соотношение путей

Если тело движется равноускоренно, начальная скорость нулевая, то пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел.

Главное запомнить

Упражнения

Поезд движется равноускоренно с ускорением a (a>0). Известно, что к концу четвертой секунды скорость поезда равна 6м/с. Что можно сказать о величине пути, пройденном за четвертую секунду? Будет ли этот путь больше, меньше или равен 6м?

Так как поезд движется с ускорением, то скорость его все время возрастает (a>0). Если к концу четвертой секунды скорость равна 6м/с, то в начале четвертой секунды она была меньше 6м/с. Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6м.

Какие из приведенных зависимостей описывают равноускоренное движение?

Уравнение скорости движущегося тела . Каково соответствующее уравнение пути?

*Автомобиль прошел за первую секунду 1м, за вторую секунду 2м, за третью секунду 3м, за четвертую секунду 4м и т.д. Можно ли считать такое движение равноускоренным?

В равноускоренном движении пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Следовательно, описанное движение не равноускоренное.

Источник

Что называется ускорением равноускоренного движения? Формулы и решение задачи

Понятие об ускорении

Движение объектов вдоль различных траекторий описывается такими величинами, как путь, скорость и ускорение. Понятия пути и скорости интуитивно понятны каждому человеку. Математическая формула, связывающая путь L и скорость v¯, имеет вид

Отметим один важный момент в этом определении: в нем речь идет о любом изменении скорости, которое может проявляться как в изменении ее модуля, так и направления.

Подставляя явное выражение для скорости в последнюю формулу, можно получить еще одно математическое равенство для ускорения через вторую производную пути:

Ускорение в системе СИ измеряют в метрах в квадратную секунду (сокращенно записывается м/с2). Так, величина 1 м/с2 означает, что скорость движения тела за каждую секунду возрастает на 1 м/с.

Равноускоренное движение и ускорение

Что называется ускорением движения равноускоренного? Понять это можно, если рассмотреть указанный тип движения.

Если движение является криволинейным, то направление ускорения изменяется, однако формула выше остается все равно справедливой, поскольку она описывает так называемую тангенциальную компоненту ускорения.

Прямолинейное движение с ускорением

Это движение происходит по прямой линии. В общем случае путь, пройденный за время t телом, рассчитывается по формуле

Приведенное кинематическое уравнение движения позволяет вычислить ускорение, если известен момент времени t и путь L, который тело прошло до этого момента. Искомое выражение имеет форму

Примером равноускоренного движения является разгон автомобиля или велосипедиста после старта. Вектор ускорения в рассмотренном случае совпадает с вектором скорости.

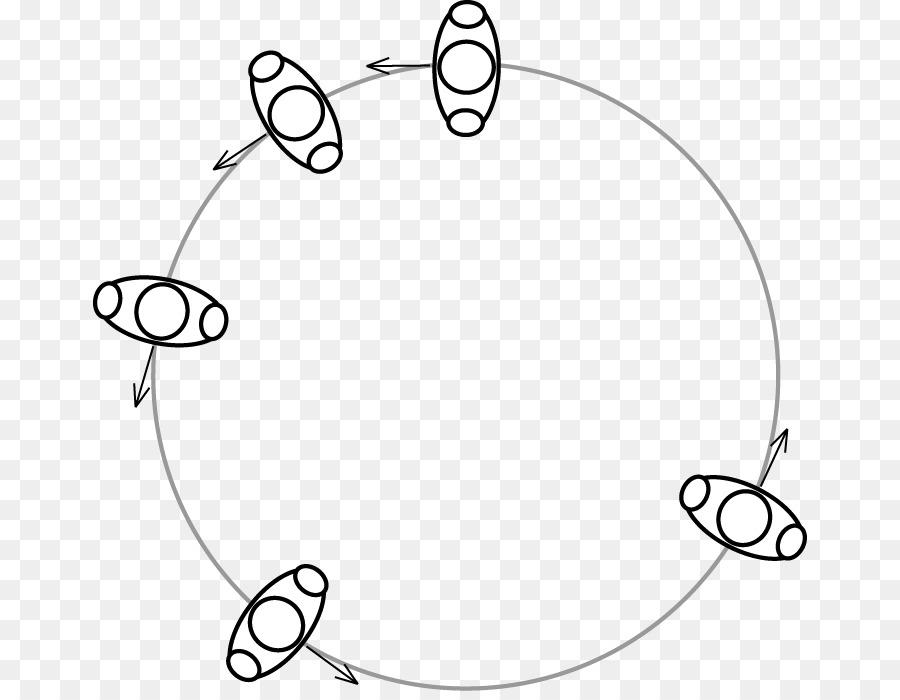
Движение по окружности с ускорением

Помимо прямолинейного движения в технике и природе встречается часто перемещение объектов по окружности. Оно может быть как равномерным, например вращение планет по своим орбитам, так и ускоренным, например вращение валов и шестерен механических станков.

Что называется ускорением равноускоренного движения тела по окружности? Его принято рассчитывать по следующей формуле:

Кинематическое уравнение движения для равноускоренного вращения имеет вид

Формула, которая связывает линейное (тангенциальное) ускорение с угловым, имеет вид

Это выражение объясняет, почему при вращениях тел удобно пользоваться угловой характеристикой α, а не линейной величиной a. В то время как α является постоянным, a зависит от расстояния r до оси вращения.

Решение задачи на определение ускорения

Рассмотрев вопрос, что называется ускорением равноускоренного движения, решим такую задачу: автомобиль, начиная движение с места по прямой дороге, прошел за первые 10 секунд путь на 100 метров больше, чем за первые 5 секунд. С каким ускорением он двигался?

Для начала запишем рабочую формулу:

Это выражение следует из приведенной выше в статье формулы для пути при равноускоренном прямолинейном движении, если учесть, что начальная скорость v0 равна нулю.

Вычитая первое равенство из второго и подставляя значения из условия задачи, получаем:

Таким образом, за каждую секунду своего движения автомобиль увеличивал скорость на 2,67 м/с.

Источник

Ускорение при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v ₀ — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

v_x — проекция скорости тела в данный момент времени, v_0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

Направление вектора ускорения

Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают ( а ↑↑ v ).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу ( а ↑↓ v ).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (a_x=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t₁ = 1 и t₂ = 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Запишем исходные данные:

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Внимательно прочитайте текст задани я и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

Алгоритм решения

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

Подставляем данные формулу и вычисляем модуль ускорения:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Равноускоренное движение

В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения . Для кинематического описания движения камня систему координат удобно выбрать так, чтобы одна из осей, например ось OY, была направлена параллельно вектору ускорения. Тогда криволинейное движение камня можно представить как сумму двух движений – прямолинейного равноускоренного движения вдоль оси OY и равномерного прямолинейного движения в перпендикулярном направлении, т. е. вдоль оси OX (рис. 1.4.1).

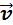
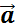
Таким образом, изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости и ускорения направлены вдоль прямой движения. Поэтому скорость υ и ускорение a в проекциях на направление движения можно рассматривать как алгебраические величины.

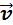
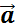
Проекции векторов скорости и ускорения на координатные оси. ax = 0, ay = –g

При равноускоренном прямолинейном движении скорость тела определяется формулой

(*)

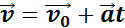
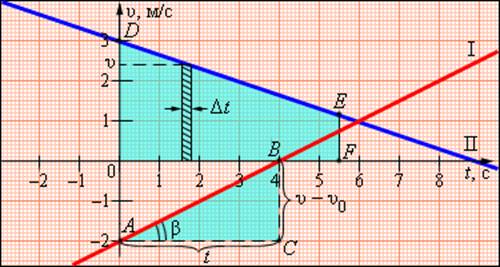
В этой формуле υ₀ – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. 1.4.2).

Графики скорости равноускоренного движения

По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. 1.4.2 для графика I. Ускорение численно равно отношению сторон треугольника ABC:

Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.

Для графика II: υ₀ = 3 м/с, a = –1/3 м/с 2

График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной полоски (рис. 1.4.2). Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены для графика II на рис. 1.4.2. Время t принято равным 5,5 с.

Так как υ – υ₀ = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:

(**)

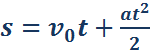
Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y₀ прибавить перемещение за время t:

(***)

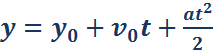
Это выражение называют законом равноускоренного движения.

При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ₀ и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде

Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ₀, ускорение a и перемещение s:

Если начальная скорость υ₀ равна нулю, эти формулы принимают вид

Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ₀, υ, s, a, y₀ являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.

Источник