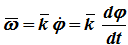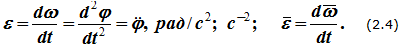Что называют угловой скоростью вращательного движения

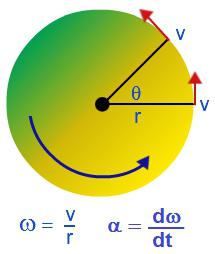
Угловая скорость

градус/с, оборот/с, оборот/мин

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Единица измерения угловой скорости, принятая в системах СИ и СГС — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто «вручную», подсчитывая число оборотов за единицу времени.

Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью , определяется формулой:

где — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) от оси вращения можно считать так: Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.

Связь с конечным поворотом в пространстве

См. также

Литература

Полезное

Смотреть что такое «Угловая скорость» в других словарях:

УГЛОВАЯ СКОРОСТЬ — векторная величина, характеризующая быстроту вращения твёрдого тела. При равномерном вращении тела вокруг неподвижной оси численно его У. с. w=Dj/Dt, где Dj приращение угла поворота j за промежуток времени Dt, а в общем случае w=dj/dt. Вектор У.… … Физическая энциклопедия

УГЛОВАЯ СКОРОСТЬ — УГЛОВАЯ СКОРОСТЬ, скорость изменения угловой позиции предмета относительно фиксированной точки. Средняя величина угловой скорости w предмета, движущегося от угла q1 до угла q2 за время t выражается как (q2 q1)w)/t. Мгновенной угловой скоростью… … Научно-технический энциклопедический словарь

УГЛОВАЯ СКОРОСТЬ — УГЛОВАЯ СКОРОСТЬ, величина, характеризующая быстроту вращения твердого тела. При равномерном вращении тела вокруг неподвижной оси абсолютная величина его угловой скорости w=Dj/Dt, где Dj приращение угла поворота за промежуток времени Dt … Современная энциклопедия

угловая скорость — Кинематическая мера вращательного движения тела, выражаемая вектором, равным по модулю отношению элементарного угла поворота тела к элементарному промежутку времени, за который совершается этот поворот, и направленным вдоль мгновенной оси… … Справочник технического переводчика

угловая скорость — векторная величина, характеризующая быстроту вращения твердого тела. При равномерном вращении тела вокруг неподвижной оси абсолютная величина его угловой скорости ω = Δφ/Δt, где Δφ приращение угла поворота за промежуток времени Δt. * * * УГЛОВАЯ … Энциклопедический словарь

угловая скорость — kampinis greitis statusas T sritis automatika atitikmenys: angl. angular speed; angular velocity vok. Winkelgeschwindigkeit, f rus. угловая скорость, f pranc. vitesse angulaire, f … Automatikos terminų žodynas

угловая скорость — kampinis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Vektorinis dydis, lygus kūno pasisukimo kampo pirmajai išvestinei pagal laiką: ω = dφ/dt; čia dφ – pasisukimo kampo pokytis, dt – laiko tarpas. Kai kūnas sukasi tolygiai … Penkiakalbis aiškinamasis metrologijos terminų žodynas

угловая скорость — kampinis greitis statusas T sritis fizika atitikmenys: angl. angular speed; angular velocity vok. Winkelgeschwindigkeit, f rus. угловая скорость, f pranc. vitesse angulaire, f … Fizikos terminų žodynas

Угловая скорость — величина, характеризующая быстроту вращения твёрдого тела. При равномерном вращении тела вокруг неподвижной оси численно его У. с. ω =Δφ/ Δt, где Δφ приращение угла поворота φ за промежуток времени Δt. В общем случае У. с. численно равна… … Большая советская энциклопедия

Источник

Все об угловой скорости — определение, единица измерения, методы расчета

Что такое угловая скорость

​Угловая скорость (обозначается как \(\omega\) ) — векторная величина, характеризующая скорость и направление изменения угла поворота со временем.

Модуль угловой скорости для вращательного движения совпадает с мгновенной угловой частотой вращения, а направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта.

Единица измерения

В Международной системе единиц (СИ) принятой единицей измерения угловой скорости является радиан в секунду (рад/с)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Формула угловой скорости

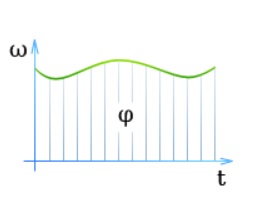
Зависимость угловой скорости от времени

Зависимость \(\varphi \) от \(\mathcal t\) наглядно показана на графике:

Угол, на который повернулось тело, характеризуется площадью под кривой.

Угловая скорость вращения, формула

Через частоту

\(\mathcal n\) — частота вращения \((1/с)\)

\(\pi\) — число Пи ( \(\approx 3,14\) )

\(T \) — период вращения (время, за которое тело совершает один оборот)

Через радиус

\(v\) — линейная скорость(м/с)

\(R\) — радиус окружности (м)

Как определить направление угловой скорости

Направление скорости в физике можно определять двумя способами:

Связь линейной и угловой скорости

Линейная скорость \((v)\) тела, расположенного на расстоянии \(R\) от оси вращения, прямо пропорциональна угловой скорости.

\(R\) — радиус окружности (м)

Чему равна мгновенная угловая скорость

Мгновенную угловую скорость нужно находить как предел, к которому стремится средняя угловая скорость при \(\triangle\mathcal t\rightarrow0\) :

Источник

Угловая скорость.

Угловой скоростью называется величина, численно равная скорости точек, расположенных от оси на расстоянии единицы длины.

При вращении тела вокруг неподвижной оси АВ каждая точка тела М описывает окружность, перпендикулярную к оси, центр Р которой лежит на оси.

Скорость точки M направлена нормально к плоскости МАВ в сторону вращения. Равномерное вращение точки характеризуется постоянной угловой скоростью.

Угловой скоростью тела называют отношение угла поворота к интервалу времени, в течение которого совершен этот поворот. Если угловую скорость обозначить через w, то:

Угловая скорость выражается в радианах в секунду (рад/с).

При равномерном вращении, когда известна угловая скорость в начальный момент времени t₀ = 0, можно определить угол поворота тела за время t и тем самым положение точек тела:

За один период (промежуток времени Т, в течение которого тело совершает один оборот по окружности) угол поворота φ равен 2π рад: 2π = wT, откуда:

Связь угловой скорости с периодом Т и частотой вращения ν выражается соотношением:

А связь между линейной и угловой скоростями определяется соотношением:

Источник

iSopromat.ru

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела:

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени.

Обозначение: ω (омега).

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

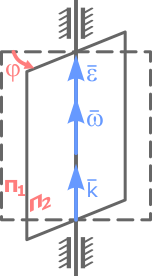
Быстрота изменения угла φ (перемещения из положения П₁ в положение П₂) – это и есть угловая скорость:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

Приняв k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

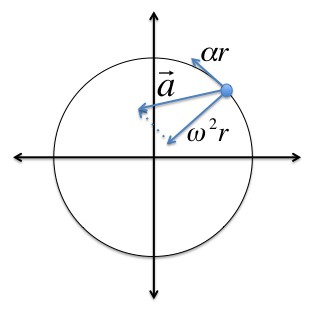
Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает, а при отрицательном вращение замедляется.

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Вращательное движение и угловая скорость твердого тела

В этой статье речь пойдет о физических величинах, которые характеризуют вращательное движение тела: угловая скорость, угловое перемещение, угловое ускорение, момент сил.

Твердым телом называют совокупность жестко связанных материальных точек. Когда твердое тело производит вращение относительно какой-либо оси, отдельные материальные точки, из которых оно складывается, двигаются по окружностям разных радиусов.

Угловое перемещение

Однако, анализируя движение отдельных материальных точек, можно установить, что за одинаковый промежуток времени все они поворачиваются вокруг оси на одинаковый угол. То есть для описания вращения твердого тела удобно пользоваться такой физической величиной, как угловое перемещение:

Угловая скорость и угловое ускорение

Вращательное движение можно охарактеризовать угловой скоростью: ω = ∆φ/∆t.

Угловая скорость характеризует скорость вращения тела и равняется отношению изменения угла поворота ко времени, за которое оно произошло. Измеряется в радианах за секунду: [ω] = рад/с.

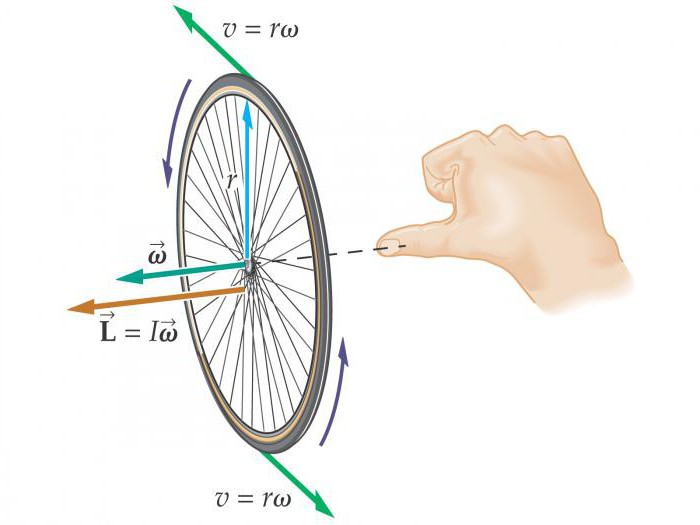
Угловая скорость вращения связана с линейной скоростью следующим соотношением: v = Rω, где R – радиус окружности, по которой двигается тело.

Угловая скорость и угловое ускорение являются псевдовекторами, направление которых зависит от направления вращения. Его можно определить по правилу правого винта.

Равномерное вращательное движение

Равномерное вращательное движение осуществляется с постоянной угловой скоростью и описывается такими уравнениями: ε = 0, ω = const, φ = φ₀ + ωt, где φ₀ – начальное значение угла поворота.

Равноускоренное вращательное движение

Равноускоренное вращательное движение происходит с постоянным угловым ускорением и описывается такими уравнениями: ε = const, ω = ω₀+ εt, φ = φ₀ + ω₀t + εt 2 /2.

Во время вращения твердого тела центростремительное ускорение каждой точки этого тела можно найти так: ɑ_ц = v 2 /R = (ωR) 2 /R = ω 2 R.

Когда вращение твердого тела ускоренное, можно найти тангенциальное ускорение его точек по формуле: ɑ_t = ∆v/∆t= ∆(ωR)/∆t= R(∆ω/∆t) = Rε.

Момент сил

Если, рассматривая физическую проблему, мы имеем дело не с материальной точкой, а с твердым телом, то действие нескольких сил на него, приложенных к различным точкам этого тела, нельзя свести к действию одной силы. В этом случае рассматривают момент сил.

Примеры решения задач

Задача 1. Ротор центрифуги делает 2•10 4 об/мин. После того как выключили двигатель, его вращение прекращается через 8 мин. Найдите угловое ускорение, а также число оборотов, которое совершает ротор с момента выключения двигателя до его полной остановки, считая, что движение ротора равноускоренное.

Отсюда, учитывая, что в конце движения скорость равна нулю, найдем: ε = ω₀/t = 2πn/t.

Переведя данные задачи в систему единиц СИ (n = 333 об/с; t = 480 с), получим: ε = 2π333/480 = 4,36(рад/с 2 ).

Угол поворота ротора центрифуги за время t будет: φ(t)= φ₀ + ω₀t + εt 2 /2. Учитывая выражение для углового ускорения и то, что φ₀ = 0, находим: φ(t)= ω₀t/2 = πnt.

Количество оборотов ротора за это время будет: N = φ(t)/2π = πnt/2π = nt = 8•10 4 (об.).

Ответ: угловое ускорение равно 4,36 рад/с 2 ; количество оборотов, сделанное ротором с момента выключения двигателя до его полной остановки, равно 8•10 4 об.

Задача 2. Диск, имеющий массу 1 кг и радиус 20 см, вращается с частотой 120 об. в минуту. Под действием тормозного устройства на край диска начала действовать сила трения 10 Н. Найдите время остановки диска, после того как на него стала действовать сила трения.

Найдем тормозной момент сил, действующий на диск: M = RF.

Найдем угловое ускорение диска: ε = M/I = FR/mR 2 = F/mR.

Сделаем вычисления: t = 2πv/ ε = 2πvmR/F = 6,28•2•1•0,2/10 = 2,5 (с).

Ответ: время остановки равно 2,5 с.

Источник