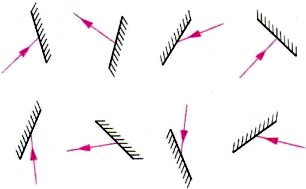
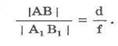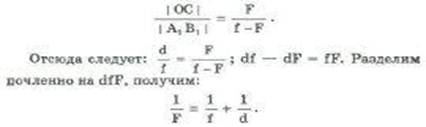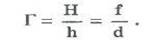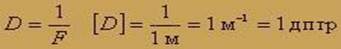Что называют углом падения углом
УГОЛ ПАДЕНИЯ
Смотреть что такое «УГОЛ ПАДЕНИЯ» в других словарях:
угол падения — 1. Угол между лучом падающей волны и нормалью к поверхности раздела сред. 2. Угол между акустической осью падающего пучка и нормалью к поверхности раздела сред. [BS EN 1330 4:2000. Non destructive testing Terminology Part 4: Terms used in… … Справочник технического переводчика
УГОЛ ПАДЕНИЯ — (Angle of falling of a shot) угол, образуемый прицельной линией с касательной к траектории в точке падения снаряда. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 Угол падения угол межд … Морской словарь
УГОЛ ПАДЕНИЯ — «УГОЛ ПАДЕНИЯ», СССР, ЛЕНФИЛЬМ, 1969 1970, ч/б, 142 мин. Историческая военная драма. По одноименному роману В.Кочетова. В основе сюжета оборона Петрограда от войск Юденича (1919). В ролях: Павел Кашлаков (см. КАШЛАКОВ Павел), Георгий Куликов (см … Энциклопедия кино
угол падения — 3.22 угол падения: По ГОСТ 7427. Источник … Словарь-справочник терминов нормативно-технической документации
угол падения ( b) — 2.3.7 угол падения ( b): Угол, образуемый осью освещения и исходной осью. Угол падения обычно не превышает 90°, однако его полные значения определяются следующими пределами: 0° Словарь-справочник терминов нормативно-технической документации
угол падения — kritimo kampas statusas T sritis Gynyba apibrėžtis Kampas tarp trajektorijos liestinės kritimo taške ir pabūklo horizonto. simbolis( iai) θ atitikmenys: angl. angle of fall; angle of grazing rus. угол падения … Artilerijos terminų žodynas
угол падения — kritimo kampas statusas T sritis fizika atitikmenys: angl. incidence angle vok. Einfallswinkel, m; Einfallwinkel, m rus. угол падения, m pranc. angle d’incidence, m … Fizikos terminų žodynas
Угол падения — Жарг. мол. Шутл. 1. Место проведения вечеринки со спиртным. 2. Пивная. 3. Винный магазин. Максимов, 437 … Большой словарь русских поговорок
УГОЛ ПАДЕНИЯ — 1970, 2 серии, 1 с. 72 мин., 2 с. 70 мин., ч/б, ш/э, 2то. жанр: драма. реж. Геннадий Казанский, сц. Всеволод Кочетов, Геннадий Казанский (по одноименному роману Всеволода Кочетова), опер. Дмитрий Месхиев, худ. Семен Малкин, комп. Надежда… … Ленфильм. Аннотированный каталог фильмов (1918-2003)
Законы отражения
1. Падающий луч, отражающий луч и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости.
2. Угол отражения γ равен углу падения α:
4. Закон преломления. Предельный угол. Полное внутреннее отпажение.
Преломление света — явление, при котором луч света, переходя из одной среды в другую, изменяет направление на границе этих сред.
закон преломления света
Преломление света происходит по следующему закону:
Падающий и преломленный лучи и перпендикуляр, проведенный к границе раздела двух сред в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред:
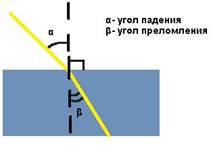
где α — угол падения,
β — угол преломления,
n — постоянная величина, не зависящая от угла падения.
При изменении угла падения изменяется и угол преломления. Чем больше угол падения, тем больше угол преломления.
Если свет идет из среды оптически менее плотной в более плотную среду, то угол преломления всегда меньше угла падения: β
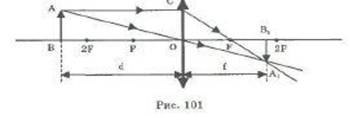
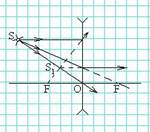
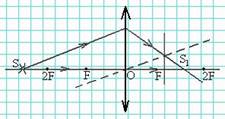
Формула тонкой линзы связывает d (расстояние от предмета до оптического центра линзы), f (расстояние от оптического центра до изображения) с фокусным расстоянием F (рис. 101).
Треугольник АВО подобен треугольнику OB1A1. Из подобия следует, что
Треугольник OCF подобен треугольнику FB1A1. Из подобия следует, что
Это и есть формула тонкой линзы.
Отношение размера изображения Н к линейному размеру предмета h называют линейным увеличением линзы Г.
Обозначают оптическую силу буквой D. За единицу оптической силы взята диоптрия (дптр).
Оптическую силу собирающих линз считают положительной, а рассеивающих линз – отрицательной.
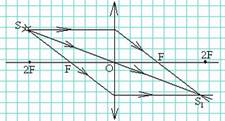
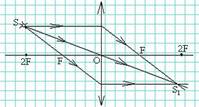
6. Оптические точки и плоскости линзы. Виды линз. Построение изображенийв собирающих и рассеивающих линзах.
Несмотря на огромное разнообразие, видов линз в физике различают всего два: выпуклые и вогнутые, или собирающие и рассеивающие линзы соответственно.
У выпуклой, то есть собирающей линзы края намного тоньше, чем середина. Собирающая линза в разрезе – это две призмы, соединенные основаниями, поэтому все проходящие сквозь нее лучи сходятся к центру линзы.
У вогнутой линзы края, наоборот, всегда толще, чем середина. Рассеивающую линзу можно представить в виде двух соединенных вершинами призм, и, соответственно, лучи, проходящие через такую линзу, будут расходиться от центра.
Так же есть двояковогнутые, двояковыпуклые, выпукло-вогнутые линзы.
7. Погрешности линз. Сферическая и хроматическая аберрации. Кома. Дисторсия.
Аберрация — это отклонение геометрии объекта съемки или цветов по контуру снимаемых предметов. Аберрация возникает из-за несовершенства отражающих и преломляющих поверхностей объектива.
Хроматическая аберрация — это искажения, обусловленные зависимостью показателя преломления прозрачных сред оптической системы от длинны волны проходящего через нее света.
Сферические аберрации возникают из-за того, что линза сферической формы преломляет свет, падающий на нее около края сильнее, чем свет, который попадает по центру или недалеко от него. В результате изображение перестает быть сфокусированным в одной точке. Если смотреть на точку сквозь объектив со сферическими аберрациями, она будет иметь достаточно однородный ореол. Эффект проявляется и в центре, и по краям изображения.
Отличительной особенностью сферических аберраций является то, что их количество снижается на закрытых диафрагмах, когда края линзы заблокированы
§ 65. Отражение света. Закон отражения света
Вам уже известно, что свет от источника или от освещенного тела воспринимается человеком, если лучи света попадают в глаза. Как будет вести себя свет, если на его пути имеется преграда? Чтобы узнать это, проделаем следующий опыт.
От источника S направим через щель пучок света на экран. Экран будет освещен, но между источником и экраном мы ничего не увидим (рис. 134, а). Теперь между источником и экраном разместим какой-либо предмет: руку, листок бумаги. В этом случае излучение, достигнув поверхности предмета, отражается, изменяет своё направление и попадает в наши глаза, т. е. он становится виден.
Рис. 134. Падение лучей света на экран
Если запылить воздух между экраном и источником света, то становится видимым весь пучок света (рис. 134, б). Пылинки отражают свет и направляют его в глаза наблюдателя.
Это явление часто наблюдается, когда лучи солнца проникают в запылённый воздух комнаты.
Известно, что в солнечный день при помощи зеркала можно получить световой «зайчик» на стене, полу, потолке. Объясняется это тем, что пучок света, падая на зеркало, отражается от него, т. е. изменяет своё направление. Световой «зайчик» — это след отражённого пучка света на каком-либо экране. На рисунке 135 показано отражение света от зеркальной поверхности.
Рис. 135. Отражение света от зеркальной поверхности
Линия MN — поверхность раздела двух сред (воздух, зеркало). На эту поверхность из точки S падает пучок света. Его направление задано лучом SO. Направление отражённого пучка показано лучом ОВ. Луч SO — падающий луч, луч ОВ — отражённый луч. Из точки падения луча О проведён перпендикуляр ОС к поверхности MN. Угол SOC, образованный падающим лучом SO и перпендикуляром, называется углом падения (α). Угол СОВ, образованный тем же перпендикуляром ОС и отражённым лучом, называется углом отражения (β).
При изменении угла падения луча будет меняться и угол отражения. Это явление удобно наблюдать на специальном приборе (рис. 136). Прибор представляет собой диск на подставке. На диск нанесена круговая шкала с ценой деления 10°. По краю диска можно передвигать осветитель, дающий узкий пучок света. Закрепим в центре диска зеркальную пластинку и направим на неё пучок света (см. рис. 136).
Рис. 136. Прибор для наблюдения изменения угла падения света
Если пучок света падает под углом 45°, то под таким же углом он и отражается от зеркала. Передвигая осветитель по краю диска, будем менять угол падения луча и каждый раз отмечать соответствующий ему угол отражения. Во всех случаях угол отражения равен углу падения луча. При этом лучи отражённый и падающий лежат в одной плоскости с перпендикуляром, проведённым к зеркалу в точке падения луча. Таким образом, отражение света происходит по следующему закону: лучи падающий и отражённый лежат в одной плоскости с перпендикуляром, проведённым к границе раздела двух сред в точке падения луча.
Угол падения α равен углу отражения β.
Если луч падает на зеркало в направлении ВО (см. рис. 135), то отражённый луч пойдёт в направлении OS. Следовательно, падающий и отражённый лучи могут меняться местами. Это свойство лучей (падающего и отражённого) называется обратимостью световых лучей.
Всякая незеркальная, т. е. шероховатая, негладкая, поверхность рассеивает свет, так как на ней имеются небольшие выступы и углубления.
Такую поверхность можно представить в виде целого ряда малых плоских поверхностей, расположенных под разными углами друг к другу. Поэтому падающий на такую поверхность свет отражается по разным направлениям.
Вопросы
Упражнение 45
Полное отражение



Наклонное падение УЗВ на границу раздела двух сред (общий случай)
На отражении упругих волн от несплошностей основана выявляемость дефектов в эхо-дефектоскопии, так как по своим акустическим свойствам несплошности отличаются от основного материала.
Рассмотрим в упрощенном виде основные явления, происходящие при падении ультразвуковой волны на границу раздела двух сред, имеющих акустические сопротивления Z1 и Z2.
При падении продольной волны из одной твердой среды на границу раздела с другой твердой средой образуются следующие волны (рисунок 29):
сl, β – скорость и угол падающей продольной волны;
сl1, βl – скорость и угол отраженной продольной волны;
сt1, βt – скорость и угол отраженной поперечной волны, образовавшейся в результате трансформации продольной волны;
сl2, αl2 – скорость и угол прошедшей во вторую среду преломленной продольной волны;
| Рисунок 29 – Отражение, преломление, трансформация УЗВ |
сt2, α – скорость и угол прошедшей во вторую среду преломленной поперечной волны, образовавшейся в результате трансформации продольной волны.
Если продольная упругая волна l со скоростью сl падает на границу раздела двух твердых сред под углом, отличным от прямого, то отраженная и прошедшая волны преломляются и трансформируются на продольные l1, l2 и сдвиговые t1, t2волны, распространяющиеся в первой и второй средах под различными углами. Для обеспечения падения продольных волн под углом между пьезоэлементом и контролируемой деталью располагают призму из органического стекла.
Углы отсчитываются от нормали, которая представляет собой перпендикуляр, восстановленный к разделу сред. Угол β между падающим лучом сl и перпендикуляром MN к поверхности раздела в точке О называется углом падения (для преобразователей – угол призмы). Под углом падения ультразвуковой волны в акустике понимают угол, образованный нормалью к границе раздела, проходящей через точку падения луча, и направлением распространения пучка. Углы αl2,α – углы преломления (углы ввода соответственно продольной и поперечной волны).
В общем случае на границе раздела двух твердых сред могут происходить три явления: отражение, преломление и трансформация волн.
Отражением называют изменение направления УЗВ на границе раздела, при котором волна не переходит в другую среду.
Преломлением называют изменение направления УЗВ на границе раздела, при котором волна переходит в другую среду.
| Рисунок 30 – Преломление света |
Из курса физики мы знаем, что наблюдается кажущееся изменение формы предметов, их расположения и размеров. В этом нас могут убедить простые наблюдения (рисунок 30). Если посмотреть на сосуд сбоку, то можно заметить, что часть соломинки, находящаяся в воде, кажется сдвинутой в сторону. Эти явления объясняются изменением направления лучей на границе двух сред – преломлением света.
Свойства акустических волн подчиняются законам геометрической оптики в случае падения УЗВ на акустически зеркальную поверхность раздела.
Преломление ультразвуковых волн, по аналогии с законами геометрической оптики, при переходе из одной среды в другую вызвано различием в скоростях распространения волн в двух разных средах. Закон преломления формулируется так: отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред.
где n – относительный показатель преломления или коэффициентом преломления первой среды по отношению ко второй (постоянная величина, не зависящая от угла падения).
Убедиться в справедливости закона преломления можно экспериментально, измеряя углы падения и преломления и вычисляя отношение их синусов при различных углах падения. Это отношение остается неизменным.
Показатель преломления n равен отношению скоростей волн в средах, на границе между которыми происходит преломление. Скорость распространения волн в какой-либо данной среде зависит от физического состояния среды: температуры вещества, его плотности, наличия в нем упругих напряжений. В зависимости от этого: если скорость во второй среде меньше, чем в первой, то и угол преломления α меньше угла падения β, и наоборот. При n 1 β > α.
Трансформацией называют преобразование волны одного типа в волну другого типа, происходящее на границе раздела двух сред (расщепление волны на два разных типа).
Для того, чтобы более лучше уяснить смысл критических углов, необходимо рассмотреть явление полного отражения. При прохождении продольной ультразвуковой волной границы раздела (будем рассматривать типичную границу раздела для ультразвуковых волн при вводе их в контролируемое изделие) оргстекло – сталь скорости продольной и трансформированной поперечной волн становятся больше, т.е. сl βкр1? При падении УЗВ на границу раздела двух сред ультразвуковой луч, как уже упоминалось, частично преломляется, а частично отражается от нее. При β>βкр1 преломление продольной УЗВ невозможно, значит, луч должен полностью отразится от границы раздела. Это явление называют полным отражением ультразвукового луча. Здесь нужно сделать небольшое отступление, при прохождении границы раздела возникает трансформированная поперечная волна. Чтобы и эта волна испытала полное отражение, необходимо еще дальше увеличивать угол падения β продольной волны, до тех пор, пока угол преломления поперечной волны α не достигнет 90º (рисунок 33). В этом случае наибольшему возможному углу преломления поперечной волны α=90º соответствует критический угол падения βкр2. При дальнейшем увеличении угла падения продольной УЗВ поперечная волна будет полностью отражаться от границы раздела, преломление в этом случае также невозможно.
4 Первый критический угол βкр1
Существуют условия, когда при падении продольной волны на границу раздела двух твердых сред преломленная продольная волна во вторую среду не проникает. Это происходит при увеличении угла падения β продольной волны l до значения β = βкр1 = 27°, называемого первым критическим углом.
Первым критическим углом βкр1 называется наименьший угол падения продольной волны β, при котором преломленная продольная волна l2 не будет проникать во вторую среду.
| Рисунок 31 – Первый критический угол |
Углы ввода α и αl2также увеличиваются (угол прошедшей продольной волны αl2 становится равным 90°). Отражаются в первую среду продольная волна l1и трансформированная поперечная волна t1. Причем угол отражения продольной волны βl1 равен углу падения β = βкр1 = 27° (рисунок 31).
Увеличение угла продольной преломленной волны до 90° приводит к образованию во второй среде нескольких типов – неоднородной поверхностно-продольной волны и головной волны (продольной подповерхностной волны) (рисунок 32).
| Рисунок 32 – Явления, происходящие на границе раздела оргстекло-сталь при угле падения продольной волны под первым критическим углом βкр1 = 27° |
Неоднородная поверхностно-продольная волна, состоящая из поверхностной и объемной волн называется по-другому вытекающей или ползучей. Частицы в этой волне движутся по траекториям в виде эллипсов, близких к окружностям. Скорость вытекающей волны св незначительно превышает скорость продольной волны (для стали св ≈ 1,04сl). Эти волны существуют на глубине, примерно равной длине волны, и быстро затухают. Ослабление связано с тем, что в каждой точке границы раздела генерируются поперечные волны под углом αt2, равным третьему критическому углу, называемые боковыми волнами.
Этот угол, т.е. угол, под которым из вытекающей волны генерируются поперечные волны, определяется из соотношения синусов углов падения, отражения, преломления к скоростям распространения волн в соответствующих средах (закон Снеллиуса)
Кроме вытекающей волны при падении ультразвукового пучка на границу раздела под первым критическим углом возбуждается также головная волна – продольная подповерхностная волна. Скорость этой волны равна скорости продольной волны. Своего амплитудного значения головная волна достигает под поверхностью вдоль луча с углом ввода 78°. Одновременно с возбуждением продольно-поверхностной волны образуется и обратная продольно-поверхностная волна – распространение упругого возмущения в сторону, противоположную прямому излучению. Ее амплитуда примерно в 100 раз меньше амплитуды прямой волны. Головная волна нечувствительна к неровностям поверхности и реагирует лишь на дефекты, залегающие на глубине от 4 до 10 мм под поверхностью. Для возбуждения головных волн конструируют специальные преобразователи (ПГВ).
5 Второй критический угол βкр2
Дальнейшее увеличение угла падения β продольной волны приводит к тому, что во второй среде возбуждается лишь поперечная волна. Эта ситуация имеет место при углах падения, не достигших значения второго критического угла βкр2 = 58°.
| Рисунок 33 – Второй критический угол |
При достижении угла падения β продольной волны значения второго критического угла βкр2 = 58° (рисунок 33) преломленная и трансформированная поперечная волна t2 во второй среде начинает скользить вдоль границы раздела двух сред (α = 90°) и является также неоднородной волной и быстро затухает. Сильное затухание связано с образованием головной волны, которая в свою очередь порождает семейство дифракционных боковых волн, как и в случае с первым критическим углом.
Вторым критическим углом βкр2 называется наименьший угол падения продольной волны β, при котором преломленная поперечная волна t2 не будет проникать во вторую среду.
Условия существования преломленных волн во второй среде представлены в таблице 4.
Таблица 4 – Условия существования во второй среде преломленных волн при падении продольной волны на границу раздела двух твердых сред
| Значение угла падения β | Типы преломленных волн |
| β βкр2 | – |
Таблица 5 – Соотношения между углами β и α типовых ПЭП
| Углы призмы β, град. |
| Углы ввода α, град. |
Практические выводы:
1 Свойства упругих волн используют при конструировании наклонных ПЭП для контроля продольными, поперечными и поверхностными волнами (первой средой при этом является призма из оргстекла, а вторая – контролируемое изделие).
2 При наклонном падении ультразвуковых волн (β>0) отраженные продольные и поперечные волны существуют при любых углах падения, а существование прошедших зависит от соотношения скоростей падающей и прошедших волн.
Элементы залегания слоев



Наклонное залегание слоев
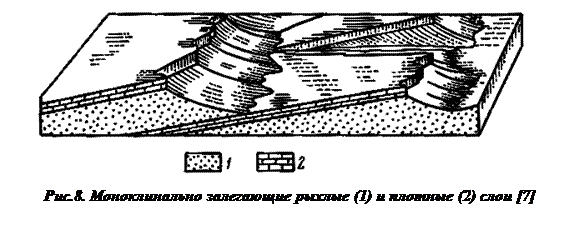
Наклонное залегание слоев – самое распространенное. Такое залегание осадочных отложений возникает в результате тектонических процессов. Однообразное наклонное залегание серий слоев, распространенное на значительной площади, называется моноклинальным залеганием (рис. 8). Моноклинальные структуры широко развиты в меловых и палеогеновых отложениях Крыма, Северного Кавказа и в некоторых других районах. Они хорошо отражаются в строении рельефа, образуя наклонные ступенчатые гряды.
Элементы залегания определяют положение слоя в пространстве, т.е. направление его вытянутости (простирание), а также направление наибольшего наклона (падение) и угол наклона (угол падения).
Простирание – это вытянутость тела в горизонтальном направлении.
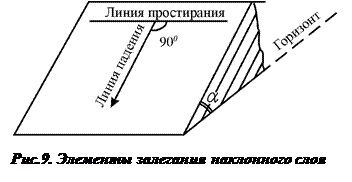
При наклонном залегании слой на небольшом участке можно охарактеризовать как наклонную плоскость, которую условно принимают за подошву или кровлю. У наклонно залегающих слоев выделяют следующие элементы: линию простирания, линию падения, угол падения (рис. 9).
Линия простирания слоя – это линия пересечения горизонтальной плоскости с поверхностью (кровлей или подошвой) пласта или любая горизонтальная линия на поверхности пласта. В пределах кровли или подошвы слоя можно провести бесконечное число линий простирания. Положение линии простирания в пространстве определяется ее азимутом.
Линия падения слоя – это линия, лежащая на поверхности слоя, перпендикулярная линии простирания и направленная по падению слоя. Ее положение в пространстве определяется азимутом и углом падения.
Угол падения слоя (α) – это угол между линией падения и ее проекцией на горизонтальную плоскость или угол, образованный поверхностью слоя (кровлей или подошвой) и горизонтальной плоскостью. Величина угла падения изменяется от 0 до 90 0 (рис.9).
Любую наклонную плоскость можно определить в пространстве (и изобразить на карте) в виде трех точек, лежащих не на одной прямой, двух пересекающихся прямых, а также двух (и более) параллельных прямых, принадлежащих данной плоскости. Для наклонного слоя такими прямыми служат две взаимно перпендикулярные линии – простирания и падения или параллельные линии простирания с известными абсолютными отметками (стратоизогипсы). Ориентировка линий простирания и падения в пространстве определяется их азимутами.
Азимут любого направления – это угол, отсчитываемый по часовой стрелке от северного направления истинного (географического) меридиана до искомого направления. Линия простирания имеет два противоположных направления, поэтому у простирания могут быть замерены два азимута, различающиеся между собой на 180°. Следовательно, азимутом простирания называется угол, заключенный между одним из направлений линии простирания и северным направлением истинного меридиана. Пример записи: аз.прост. 140Ð30 или аз.пр. 320Ð30.
Азимутом падения называется угол между проекцией линии падения на горизонтальную плоскость и северным направлением истинного меридиана. Линия падения имеет одно направление и для нее может быть замерен только один азимут, отличающийся на 90° от азимута линии простирания. Поэтому для установления положения наклонного слоя в пространстве необходимо замерить азимут линии падения и угол падения. Пример записи: аз.пад. 230Ð30.
Элементы залегания наклонного слоя замеряются с помощью горного компаса или различными косвенными способами.
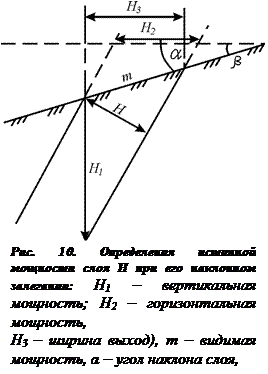
Определение истинной мощности слоя при наклонном залегании. Какое бы положение слой ни занимал в пространстве, кратчайшее расстояние между его кровлей и подошвой будет называться истинной мощностью (H). Кроме истинной мощности в наклонных слоях выделяются видимая, вертикальная, горизонтальная мощности и ширина выхода слоя на карте или плане (рис.10).
Видимая мощность (m) – кратчайшее расстояние от кровли до подошвы на срезе слоя рельефом. Вертикальная мощность (H1) – расстояние между кровлей и подошвой по вертикали. Горизонтальная мощность (Н2) – расстояние от кровли до подошвы в горизонтальном направлении, перпендикулярном простиранию. Ширина выхода (Н3) – это проекция видимой мощности на горизонтальную плоскость или ширина слоя на карте, или плане (рис. 10). Ширина выхода слоя на земной поверхности зависит от мощности слоя, угла наклона и формы рельефа. Чем больше истинная мощность слоя, тем больше при прочих равных условиях ширина его выхода на поверхность. С увеличением угла падения ширина выхода слоя на поверхность уменьшается, а при вертикальном положении слоя ширина выхода соответствует истинной мощности.
Ширина выхода зависит от угла наклона слоя и угла наклона рельефа: при совпадении направления наклона слоя и рельефа она увеличивается, а при противоположных направлениях – уменьшается. Если угол наклона рельефа больше угла падения слоя, ширина выхода слоя будет меньше истинной мощности.
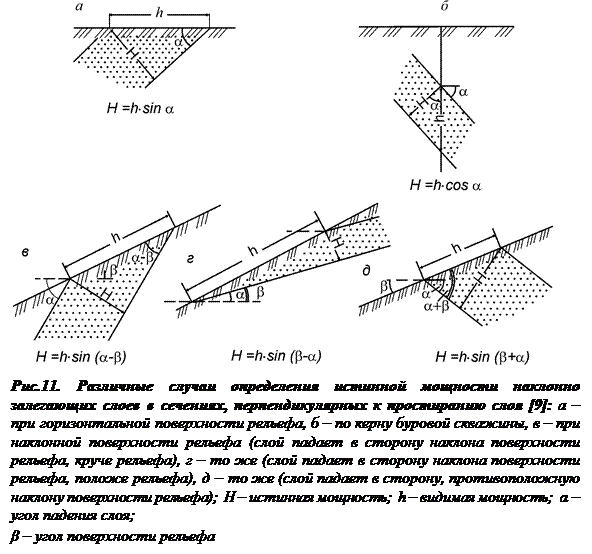
Точное определение истинной мощности слоев горных пород и пластов полезных ископаемых обязательно при любых геологических исследованиях. При малой мощности слоев ее можно замерять непосредственно в обнажениях, но при большой мощности можно замерить лишь видимую мощность, а истинную определяют путем геометрических вычислений. На рис. 11 показаны различные случаи вычисления истинной мощности в сечениях, ориентированных перпендикулярно к линии простирания, по измеренной видимой мощности, углу падения слоя и углу наклона поверхности рельефа.
Если истинная мощность слоя определяется в сечении, ориентированном косо по отношению к линии простирания, то вводят соответствующие поправки на отклонение линии разреза от направления падения. Эти поправки выражаются углом у, представляющим собой разность между азимутами линий простирания и измерения. Вычисления производят по формуле Леонтовского:
m = h (sin a cos b sin g ± cos a sin b),
где m – истинная мощность; h – видимая мощность; a – угол падения пласта; b – угол наклона рельефа.
Определение заложения и решение задач с помощью заложения
Ширина выхода наклонного слоя на поверхность зависит от мощности слоя, элементов его залегания и форм рельефа. Это используют на практике для построения выхода слоя на поверхность и определения элементов залегания по его выходам на поверхность. Чтобы решать эти задачи, необходимо знать величину заложения.
В геодезии заложением рельефа называют проекцию склона на горизонтальную плоскость между двумя точками соседних горизонталей. Горизонтали – это линии пересечения горизонтальных плоскостей с поверхностью рельефа. Высота между горизонтальными плоскостями (сечение рельефа) на карте везде одинаковая, но ее ширина (заложение рельефа) разная и зависит от крутизны склонов рельефа; чем круче склон, тем меньше заложение, т.е. горизонтали на карте ближе друг к другу, и наоборот (рис. 12). Значит, величина заложения рельефа l определяется высотой сечения h и углом наклона поверхности земли b.
Заложением наклонного слоя называется проекция отрезка линии падения слоя на горизонтальную плоскость, заключенного между двумя соседними линиями простирания, проведенными по подошве или крове слоя. Величина заложения определяется следующим образом (рис. 13).
1. На отдельном листе проводят параллельные линии с высотой сечения h. Высота сечения выбирается равной сечению горизонталей, поэтому значение h равно сечению горизонталей, отложенному в масштабе карты. Расстояния между линиями (h) для карты масштаба 1:5000 при высоте сечения горизонталей 10, 50 и 100м соответственно будут равны 2, 10 и 20 мм.
2. На верхней линии произвольно выбирают точку А, из которой транспортиром откладывают истинный угол падения, и проводят линию падения mn.
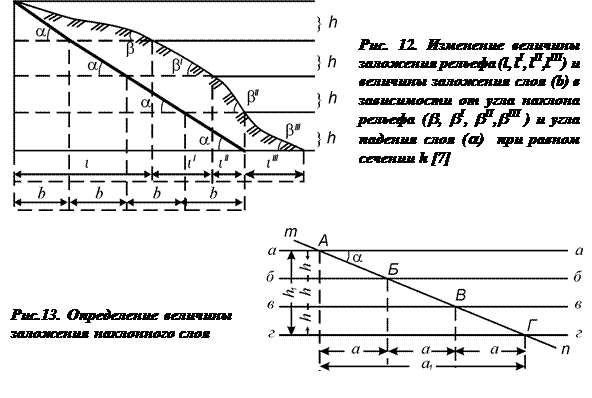
Величина заложения меняется в зависимости от угла наклона слоя, сечения горизонталей и масштаба карты.
С помощью заложения можно определять глубины скважин до кровли или подошвы пласта в определенных точках, оконтуривать площади с заданной глубиной залегания пласта, вычислять мощности слоев, а также легко определить элементы залегания пласта на карте с горизонталями по его выходу на поверхность.
Изображение наклонно залегающих слоев на карте. На геологической карте наклонные слои имеют вид полос, границы которых зависят от строения рельефа, угла наклона слоев и их мощности. При выровненном рельефе независимо от угла наклона слоев направление границ между ними будет соответствовать их простиранию, причем падение слоев при нормальном (не опрокинутом) залегании всегда будет направлено в сторону более молодых отложений. При расчлененном рельефе и наклонном залегании слоев границы между слоями пересекают горизонтали рельефа в соответствии с правилом пластовых треугольников. При вертикальном залегании слоев и любом строении рельефа границы между слоями пересекают элементы рельефа в виде прямых или изогнутых линий, соответствующих простиранию слоев. Полоса будет тем шире, чем больше мощность слоев и положе угол падения.
|
При наклонном залегании слоев и расчлененном рельефе выходы слоев на земную поверхность образуют изгибы в наиболее низкой и наиболее высокой точках рельефа. Эти изгибы как бы располагаются в вершинах треугольников, которые называются пластовыми треугольниками, форма которых связана с углом наклона моноклинально залегающих слоев. Вершина угла, лежащего в самой низкой точке рельефа, направлена по падению слоя, в самой высокой – по его восстанию. Если слои залегают вертикально, то формой их выхода на поверхность будет прямая линия.
При определении направления наклона по картам без горизонталей или с выровненным плоским рельефом следует руководствоваться общим правилом: при наклонном нормальном залегании слои наклонены в сторону расположения более молодых отложений (рис. 14). Слои не могут быть наклонены в другом направлении, так как в этом случае древние отложения залегали бы на молодых, что при нормальном налегании пород невозможно.
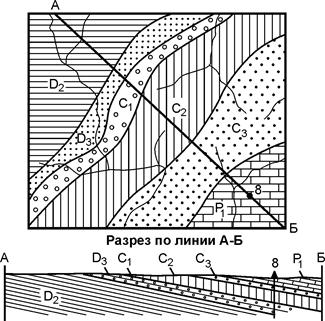
Построение геологических разрезов по картам с наклонным залеганием слоев
При построении геологических разрезов по геологическим картам с наклонным залеганием слоев линия разреза должна проводиться вкрест простирания пород, т. е. под прямым углом к линии простирания. Далее из точек пересечения линии разреза с геологическими границами на топографическом профиле с помощью транспортира откладываются истинные углы падения. Элементы залегания пород указываются на картах штриховыми знаками или определяются графическими способами. Если линия разреза расположена не вкрест простирания, а под углом к линии простирания, то на разрезе угол падения слоя будет иметь промежуточное значение между 0° и истинным углом падения. В этом случае на топографическом профиле откладываются углы падения, взятые из таблиц поправок, или определяются графически.
При наклонном залегании слоев разрезы, как правило, строятся в одинаковых горизонтальном и вертикальном масштабах. Но может возникнуть необходимость увеличения вертикального масштаба, что исказит (в сторону увеличения) истинный угол падения.
При увеличении вертикального масштаба разрезов углы падения слоя, откладываемые на топографическом профиле, находятся по таблицам поправок.
Если разрез с увеличенным вертикальным масштабом строится по косому направлению относительно линии простирания (т.е. не вкрест простирания), то вначале по таблице поправок устанавливают искаженный угол для косого направления, а затем полученное значение принимают за истинный угол падения и пересчитывают его с помощью таблиц поправок в соответствии с отношением вертикального и горизонтального масштабов.
Топографический профиль на разрезах с увеличенным вертикальным масштабом также получается искаженным, поэтому вертикальные расстояния между высотными отметками рельефа наносят на профиль не в горизонтальном масштабе, а в увеличенном вертикальном.
Точность построения разрезов с наклонным залеганием слоев во многом зависит от правильности построения топографических профилей.