Что называют тангенсом угла а где 0 меньше а меньше 180
Презентация по теме :»Синус,косинус и тангенс угла», 9-й класс.
Содержимое разработки
Синус, косинус и тангенс для угла от 0° до 180°
Не стыдно чего-нибудь не знать, но стыдно не хотеть учиться. (Сократ)
Какую полуокружность называют единичной?
Радиус равен 1,центр в начале координат, расположена в 1 и 2 координатной четверти.
Что называют синусом угла α, где 0°≤α≤180°
Синусом угла называется ордината точки
Что называют косинусом угла α, где 0°≤α≤180°
Косинусом угла называется абсцисса точки
В каких пределах находится значение синуса, косинуса?
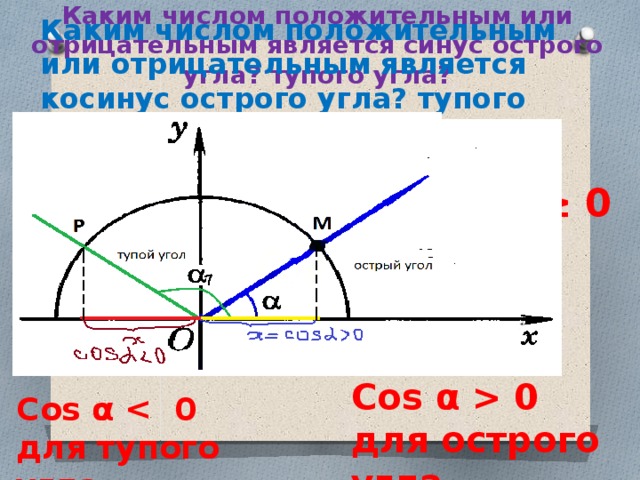
Каким числом положительным или отрицательным является косинус острого угла? тупого угла?
Каким числом положительным или отрицательным является синус острого угла? тупого угла?
Cos α 0 для острого угла
Какой формулой связаны синус и косинус одного и того же угла?
Основное тригонометрическое тождество
Что называют тангенсом угла α, где 0°≤α≤180 °
Тангенс – это отношение синуса к косинусу этого же угла(α≠90°)
Почему тангенс не определен для угла 90°?
х = cosα ≠ 0 значит α≠ 90°
Какое общее название имеют функции f(α) = sinα, g(α) = cosα, h(α) = tgα
Леонард Эйлер ввел и само понятие функции и принятую в наши дни символику.
Он придал всей тригонометрии ее современный вид.

В треугольнике АВС угол С равен 90°. ВС = 2
Презентация по геометрии «Синус, косинус и тангенс угла»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Тема урока: «Синус, косинус и тангенс угла» Самый лучший 9а класс.
Какую полуокружность называют единичной? Радиус равен 1,центр в начале координат, расположена в 1 и 2 координатной четверти. M (x; y) C (0; 1) B (-1; 0) A(1; 0) x y 0 x y D h
Что называют синусом угла α, где 0° ≤ α ≤ 180°? Синусом угла называется ордината точки sin α = y Что называют косинусом угла α, где 0° ≤ α ≤ 180°? Косинусом угла называется абсцисса точки cos α = x
В каких пределах находится значение синуса, косинуса? 0 ≤ sin α ≤ 1 − 1 ≤ cos α ≤ 1 A C (0; 1) B (-1; 0) A(1; 0) x y 0 B
Что называют тангенсом угла α, где 0° ≤ α ≤ 180°? Тангенс – это отношение синуса к косинусу этого же угла(α ≠ 90°)
Какой формулой связаны синус и косинус одного и того же угла? Основное тригонометрическое тождество sin2α+ cos2α = 1 для любого из промежутка 0 ≤ ≤ 180
В треугольнике ABC угол C равен 90°, AC = 6, AB = 10. Найдите sin B. Ответ: 0,6
В треугольнике ABC угол C равен 90°, BC = 8, AB =10. Найдите cos B. Ответ: 0,8
В треугольнике ABC угол C равен 90°, BC = 4, AC = 28. Найдите tg B. Ответ: 7
Тригонометрическая таблица 00 300 450 600 900 1200 1350 1500 1800 sin cos tg
A (x; y) x y O M (cos α; sin α) Формулы для вычисления координат точки А (x; y) – произвольная точка М (сos α; sin α) x = ОА ∙ cos y = OA ∙ sin α
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-1038777
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
В МГПУ сформулировали новые принципы повышения квалификации
Время чтения: 4 минуты
Время чтения: 2 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
В Оренбурге школьников переведут на дистанционное обучение с 9 декабря
Время чтения: 1 минута
Госдума приняла закон об использовании онлайн-ресурсов в школах
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Угол поворота
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Синус (sin) угла поворота
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Основные функции тригонометрии
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Тангенс — что это такое (отношение чего к чему) и как его найти (по формулам и по клеточкам)
Как пользоваться таблицей Брадиса.
На некоторых примерах рассмотрим, как пользоваться таблицей Брадиса.
sin 7° = 0.1219 (косинусы находятся внизу) cos 82° = 0.1392.
sin 3°42′ = 0.0645 (ниже на изображении отмечено красным) cos 80°24′ = 0.1668.
Обратите внимание, все тоже самое верно и при определении значений тангенса и котангенса.
Далее рассмотрим вариант посложнее, когда угол, который представлен в таблице не указан, значит, нужно выбирать более близкое к нему значение (из значений, которые указаны в таблице синусов и косинусов), а на разницу, которая может составлять 1′,2′,3′, берем поправку из минут (желтая графа), как видно на примере:
sin 3°45′=sin 3°42′+3′=0.0645+0.0009=0.0654 либо
sin 3°45′=sin 3°48′−3′=0.0663−0.0009=0.0654
Кроме того, нужно помнить правило: для синуса у поправки неотрицательный знак, а у косинуса неположительный.
cos 80°27′=80°24′+3′=0.1668+(-0.0009)=0.1659 либо
Решение уравнения tg x = a
| Обычная форма записи решения: |  |
| Более удобная форма записи решения |  |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
Более удобная форма записи решения:
Ограничения на число a:
Графическое обоснование решения уравнения tg x = a представлено на рисунке 3.
Частные случаи решения уравнений tg x = a
| Уравнение | Решение |
 |  |
| tg x = – 1 |  |
 |  |
| tg x = 0 |  |
 |  |
| tg x = 1 |  |
 |  |
Тангенс угла
Первые встречи с тангенсом происходят при изучении прямоугольных треугольников.
В них соотношения сторон, образующих прямой угол (катетов), и стороны, лежащей напротив угла в 90º (гипотенузы), задают важные параметры для изучения углов.
Важно, что это отвлечённые понятия, не связанные с какими-либо единицами измерения.
Введя функции угла, определяют их свойства. Некоторые полученные формулы могут иметь довольно громоздкий вид. Чтобы избежать затруднённого чтения, вводятся другие объекты.
Так произошло и с тангенсом. Ему посчастливилось получить два определения. Каждое характеризует заданное отношение по-своему. С одной стороны, рассматривается связь между катетами и острыми углами прямоугольного треугольника, с другой – даётся возможность упростить формулы, содержащие синусы и косинусы.
Мало кто задумывается, изучая тангенс в школе, что первоначально он был необходим, чтобы найти касательные линии к заданной кривой. Само понятие возникло от латинского слова tangens, которое означает «трогающий», «касающийся» и является причастием настоящего времени от tangere («трогать», «касаться»).
Тригонометрические функции и их значение в изучении геометрии
В геометрии особую роль имеют тригонометрические функции, при помощи которых определяют, как относятся между собой стороны и углы прямоугольного треугольника. Конечно, тригонометрия не стоит на месте и со времен Евклида она намного шагнула вперёд и теперь может эти функции могут выражаться через решение дифференциальных уравнений.
В данный момент используются шесть обозначений для основных тригонометрических функций, причем четыре функции из шести, они стоят в ряду последними, можно определять не только с помощью геометрии.
Синус (sin)
Косинус (cos)
Тангенс (tg/tan)
Котангенс (ctg/cot)
Секанс (sec)
Косеканс (cosec/csc) 
Рассмотрим сам прямоугольный треугольник, обозначения его сторон и углов во всех справочниках, как обычно, стандартные, какой бы стороной он не лежал бы на плоскости.
В этом треугольнике различают три угла, обозначаемые α, β, γ, при этом γ всегда 90°. Сторона, лежащая напротив прямого угла γ, называется гипотенузой, она обозначается буквой С. Угол α, с него начинаются все расчеты, находится напротив стороны а / ВС/, называемой противолежащей к этому углу, и сторона b /АС/, которая находится рядом, подлежит к этому углу и называется прилежащей.
По Евклидовой теории, которая верна до сих пор (и будет верна всегда), суммы углов такого треугольника, который находится в одной плоскости, будет равна 180 или числу π. И значение любого угла будут находиться в пределах между 0 и π /2.
Тогда тригонометрические функции можно выразить через размеры сторон этого треугольника. Так как угол α является первым и в греческом алфавите и в нашем треугольнике, начинаем знакомство с функциями через этот угол.
Эти функции можно выразить и через окружность путем задания системы координат. Задаем систему координат с центом в точке О. Угол, на который поворачивается отрезок ОА, изображенный на чертеже, будем считать произвольным, назовем его θ.
Тогда тангенсом этого угла θсчитается отношение ординаты точки А на окружности к её абсциссе. Следовательно, если ctg α = b : а, а АС = sin θ, ОС = cos θ, то tgθ = sin θ : cos θ. Аналогично получаем ctg θ = cos θ : sin θ или 1 : tgθ.
Тангенс — это отношение…
Итак, есть два определения:
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Это определение удобно использовать при изучении геометрических фигур. Оно даёт возможность, минуя вычисления гипотенузы, находить углы или катеты. Выделяя прямоугольные треугольники в произвольных фигурах, задача по изучению свойств исследуемых объектов становится проще.
Тангенс – это отношение синуса к косинусу.
Благодаря этому определению, многие тригонометрические формулы принимают более удобный вид, становятся легче воспринимаемыми.
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах ЭВМ и ПК закрепилось другое обозначение: tan(α).
Применение функции тангенса для решения задач
Что бы научиться пользоваться этой функцией, Нужно попробовать решить несколько примеров по применению этой функции.
Пример: есть два катета ВС = 7 см и АС = 12 см. Нам нужно узнать все остальные данные о треугольнике.
Первая формула, это tg α = а : b. тогда tg α = 7 :12= 0, 5833, далее для нахождения угла α используем таблицы Брадиса. На пересечении градусов и минут находим ближайшее значение угла – 0,5844, соответствующее 30° и 18′.
Находим ближайшую поправку, разную 3′. Отнимаем ее от нашего угла и получаем угол α = 30° 15′. Второй угол находим, исходя из того, что сумма всех углов должна быть не больше 180°, а угол γ = 90° по условию. Тогда угол β = 90° – 30° 15′= 59°45′.
Нам осталось найти гипотенузу с.
Можем найти её через sin α, который равен а: с, тогда с = а : sin α.
Находим sin α через таблицу Брадиса. Ближайшее значение 30° 36′, будет 0,5060, тогда не хватает 3′, Что по полям поправок равно 0,0008. Добавляем это число к найденному: 0, 5060 + 0,0008 = 0,5068. Подставляем это значение в формулу, с = 7:0,5068, с = 13, 8 см. Задача решена.
Можно искать значение углов через значение числа π, которое равно 180°. Тогда наиболее популярные углы, такие, как тангенс 30 градусов, тангенс 0 градусов, тангенс 60 градусов, тангенс 90 градусов, тангенс 45 градусов, тангенс 15 градусов, тангенс 75 градусов можно рассматривать намного проще. Нужно знать, что тангенс 0 градусов равен 0, а тангенс 90 градусов не имеет конкретного значения.
Можно найти тангенс угла 5 градусов, который равен 0, 0875 и добавлять или отнимать от наиболее часто встречающихся углов. Например угол 45 градусов, его тангенс равен 1, тогда тангенс угла 50 градусов будет равен 1, 0875. Тангенс 35 градусов можно рассчитать путем добавления к тангенсу 30 градусов угол 5 градусов, а тангенс 10 градусов это удвоение угла 5 градусов.
Для удобства есть рассчитанная таблица основных углов через значение π.
| Значение угла α (градусов) | Значение угла α в радианах | tg (тангенс) |
|---|---|---|
| Тангенс 0 | 0 | 0 |
| Тангенс 15 | π/12 | 0.2679 |
| Тангенс 30 | π/6 | 0.5774 |
| Тангенс 45 | π/4 | 1 |
| Тангенс 50 | 5π/18 | 5114 |
| Тангенс 60 | π/3 | 1.7321 |
| Тангенс 65 | 13π/36 | 2.1445 |
| Тангенс 70 | 7π/18 | 2.7475 |
| Тангенс 75 | 5π/12 | 3.7321 |
| Тангенс 90 | π/2 | – |
| Тангенс 105 | 5π/12 | -3.7321 |
| Тангенс 120 | 2π/3 | -1.7321 |
| Тангенс 135 | 3π/4 | -1 |
| Тангенс 140 | 7π/9 | -0.8391 |
| Тангенс 150 | 5π/6 | -0.5774 |
| Тангенс 180 | π | 0 |
| Тангенс 270 | 3π/2 | – |
| Тангенс 360 | 2π | 0 |
Если угол больше 90 градусов, нужно помнить, что функции имеют свойство повторяться, поэтому, если ищем тангенс 145 градусов, тогда 180 – 145 = 35 градусов, но уже со знаком «минус», это можно понять по чертежу окружности, где положительное или отрицательное значение абсциссы и ординаты. Научиться быстро пользоваться таблицами Брадиса и рассчитывать значения треугольника совсем не сложно, главное, уловить суть процесса.





























