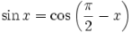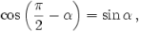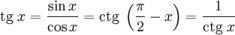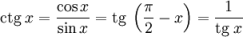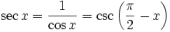Что называют тангенсом угла а где 0 меньше а меньше 180 градусов
Презентация по теме :»Синус,косинус и тангенс угла», 9-й класс.
Содержимое разработки
Синус, косинус и тангенс для угла от 0° до 180°
Не стыдно чего-нибудь не знать, но стыдно не хотеть учиться. (Сократ)
Какую полуокружность называют единичной?
Радиус равен 1,центр в начале координат, расположена в 1 и 2 координатной четверти.
Что называют синусом угла α, где 0°≤α≤180°
Синусом угла называется ордината точки
Что называют косинусом угла α, где 0°≤α≤180°
Косинусом угла называется абсцисса точки
В каких пределах находится значение синуса, косинуса?
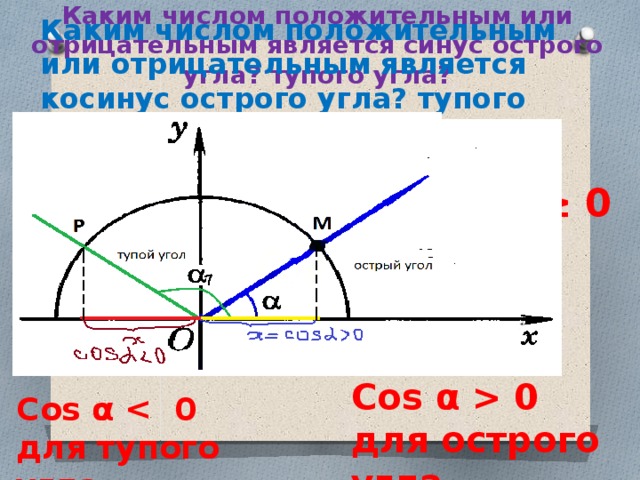
Каким числом положительным или отрицательным является косинус острого угла? тупого угла?
Каким числом положительным или отрицательным является синус острого угла? тупого угла?
Cos α 0 для острого угла
Какой формулой связаны синус и косинус одного и того же угла?
Основное тригонометрическое тождество
Что называют тангенсом угла α, где 0°≤α≤180 °
Тангенс – это отношение синуса к косинусу этого же угла(α≠90°)
Почему тангенс не определен для угла 90°?
х = cosα ≠ 0 значит α≠ 90°
Какое общее название имеют функции f(α) = sinα, g(α) = cosα, h(α) = tgα
Леонард Эйлер ввел и само понятие функции и принятую в наши дни символику.
Он придал всей тригонометрии ее современный вид.

В треугольнике АВС угол С равен 90°. ВС = 2
Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Угол поворота
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Синус (sin) угла поворота
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Основные функции тригонометрии
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа
Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа
В данной статье рассмотрим темы, которые встречаются в заданиях ЕГЭ по математике и содержатся в разделе алгебры, в ходе изучения темы подробно рассмотрим определения, используемые в теме, просмотрим рисунки, радианную меру углов, а также будем решать примерные задания. Темы, содержащиеся в статье, рассматриваются в соответствии с кодификатором, задающим элементы содержания заданий для выпускников образовательных организаций.
Переходим к более подробному изучению темы.
Для понятия о тригонометрических функциях следует рассмотреть окружность, радиус которой является единичным. У окружности есть центр, находящийся в начале координат, он расположен непосредственно на координатной плоскости. Для того, чтобы определить данную функцию, будем рассматривать вектор ОР. Он берёт начало в центре заданной окружности. Р – есть точка окружности. С помощью вектора ОР образуется угол с прилегающей осью, названной ОХ. ОР будет равен: OR = R = 1.
Рассмотрим соответствующий рисунок (рис. 1).
При проведении перпендикуляра из Р к оси ОХ получается прямоугольный треугольник, у которого есть гипотенуза и она равна единице.
При движении радиуса-вектора по часовой стрелке, будет получено отрицательное направление. А если радиус будет двигаться против часовой стрелки – положительное направление.
Для того чтобы осуществить вычисления синуса угла альфа, нужно обозначить на плоскости координату У. Как же получить это значение? Следует помнить, что в треугольнике, являющемся прямоугольным, синус произвольного угла будет равен отношению катета, являющегося противолежащим по отношению к гипотенузе. Получаем:
Радиус равен единице, исходя из этого: sin a = у0.
Тангенсом угла, являющегося произвольным, считают отношение синуса и косинуса.
Представим произвольный треугольник, при условии, что он является прямоугольным. Здесь тангенсом будет отношение катета, названного противолежащим по отношению к прилежащему катету.
Если мы будем рассматривать единичную окружность – отношение её ординаты к абсциссе.
tg a = sin a / cos a; tg a = y0 / x0.
Следовательно, тангенс может быть при нулевом значении абсциссы, при этом, угол должен быть прямым. Тангенс вправе принимать и другие значения, такие как отрицательные и положительные.
Положительное значение тангенс будет иметь в первых и третьих четвертях окружности, являющейся единичной. Отрицательным тангенс является в четвёртой и второй четвертях.
Перейдём к рассмотрению котангенса. Котангенс угла, являющегося произвольным – косинус по отношению к синусу.
При рассмотрении прямоугольного треугольника это прилежащий катет по отношению к противолежащему:
Ctg a = cos a / sin a;
Если угол альфа равен нулю, то котангенса не существует. Это обусловлено тем, что в знаменателе дроби находится ордината.
Котангенс так же как и тангенс, в четвертях окружности, имеет такие же значения.
Рассмотрим примеры заданий, а в точности — неравенства:
— Если n принадлежит Z, то:
Sin (a + 2 пn ) = sin a;
Cos ( a + 2 пn ) = cos a.
— Также, если n принадлежит Z, то:
Ctg ( a + пn ) = ctg а.
Перейдём к рассмотрению радианной меры угла. Рассмотрим единичную окружность (рис. 2).
Проводим дугу, которая будет равна радиусу окружности. Далее нужно соединить центр с концами данной дуги с помощью радиана. Один градус будет равен п 180 радиан. Один радиан соответственно, будет равен 180п. При этом, окружность будет равняться 2п.
Само понятие радиана открыл Томас Мюир и Джеймсон Томпсон в 1870 году. Таким образом, учёные измеряли углы на протяжении большого количества времени. К примеру, учёный Эйлер проводил исследования, он измерял углы с помощью длины дуги, которая отрезана в окружности, являющейся единичной.
Решим задачу ЕГЭ по математике на данную тему.
Нужно найти углы, при мере радиуса равной п / 2, п / 4, п / 8.
П / 2 * 180 / п = 90 градусов.
П / 4 * 180 / п = 45 градусов.
П / 8 * 180 / п = 22, 5 градуса.
Следует запомнить, что:
— 30 градусов равны п / 6;
— 45 градусов равны п / 4;
— 60 градусов равны п / 3;
— 90 градусов равны п / 2;
— 120 градусов равны 4п / 6;
— 180 градусов равны п.
Синус, тангенс, косинус, котангенс числа
Определением вышеописанных понятий считают число, равное синусу, косинусу, тангенсу и котангенсу в t радиан.
Синусом, косинусом, тангенсом и котангенсом числа t считают число, равное синусу, косинусу, тангенсу и котангенсу в t радиан.
Рассмотрим пример. Для любого действительного числа на окружности, являющейся единичной, определять точку. При этом, центр окружности должен находиться в начале системы координат. Все данные находят с помощью данной точки.
Начальной точкой окружности является точка А. Её координатами будут ( 1; 0 ). Пусть t – положительное число. Данному числу будет соответствовать точка, в неё осуществит переход изначальная точка. Если t отрицательное, то ему будет соответствовать точка, в которую осуществит переход исходная точка при направлении против часовой стрелки.
Рассмотрим определения основных понятий темы.
Синусом числа t является ордината точки окружности, являющейся единичной, она соответствует числу t. То есть sin t = y.
Косинусом числа t называют абсциссу точки окружности, являющейся единичной, она соответствует числу t. Получается: cos t = x.
Тангенсом числа t считают отношение ординаты к абсциссе точки окружности, являющейся единичной, она соответствует числу t. То есть: tg t = yx = sin t cos t.
Следует запомнить данные определения, а также необходимые неравенства, они пригодятся при решении заданий ЕГЭ по математике.
Данные определения не противоречат определению, которое дано в начале этой темы. Точка, лежащая на окружности, соответствует числу t, а также имеет совпадение с точкой. В эту точку переходит исходная точка, это происходит после осуществления поворота на угол, равный t радиан.
В процессе подготовки к экзамену рекомендуем внимательно просмотреть демоверсию ЕГЭ по математике базового уровня, а также решить примерные задания по теме. В демонстрационном варианте содержатся необходимые пояснения к ЕГЭ. Его назначением является ознакомление с примерным содержанием КИМОВ, заданиями, а также уровнем их сложности.
Таблица тангенсов, тангенс угла
Содержание статьи тангенс угла
Из четырёх наиболее используемых тригонометрических таблиц в справочнике Брадиса является ТАБЛИЦА ТАНГЕНСОВ. И тангенс и котангенс – это производные от синуса и косинуса и очень удобно, когда есть готовые рассчитанные значения для этих величин
Тригонометрические функции, что это такое и их значение в изучении геометрии
В геометрии особую роль имеют тригонометрические функции, при помощи которых определяют, как относятся между собой стороны и углы прямоугольного треугольника. Конечно, тригонометрия не стоит на месте и со времен Евклида она намного шагнула вперёд и теперь может эти функции могут выражаться через решение дифференциальных уравнений.
Синус (sin)
Косинус (cos)
Тангенс (tg/tan)
Котангенс (ctg/cot)
Секанс (sec)
Косеканс (cosec/csc) 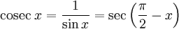
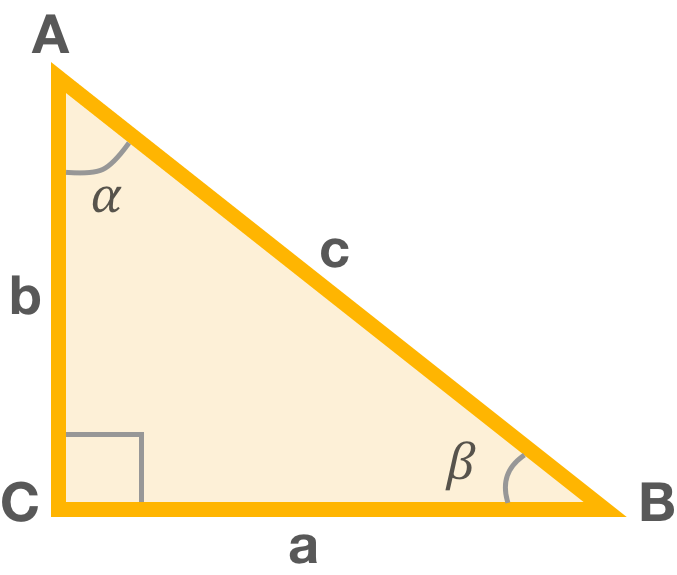
Рассмотрим сам прямоугольный треугольник, обозначения его сторон и углов во всех справочниках, как обычно, стандартные, какой бы стороной он не лежал бы на плоскости.
В этом треугольнике различают три угла, обозначаемые α, β, γ, при этом γ всегда 90°. Сторона, лежащая напротив прямого угла γ, называется гипотенузой, она обозначается буквой С. Угол α, с него начинаются все расчеты, находится напротив стороны а / ВС/, называемой противолежащей к этому углу, и сторона b /АС/, которая находится рядом, подлежит к этому углу и называется прилежащей.
По Евклидовой теории, которая верна до сих пор (и будет верна всегда), суммы углов такого треугольника, который находится в одной плоскости, будет равна 180 или числу π. И значение любого угла будут находиться в пределах между 0 и π /2.
Тогда тригонометрические функции можно выразить через размеры сторон этого треугольника. Так как угол α является первым и в греческом алфавите и в нашем треугольнике, начинаем знакомство с функциями через этот угол.
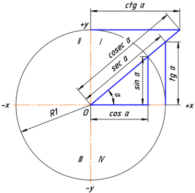
Эти функции можно выразить и через окружность путем задания системы координат. Задаем систему координат с центом в точке О. Угол, на который поворачивается отрезок ОА, изображенный на чертеже, будем считать произвольным, назовем его θ.
Тогда тангенсом этого угла θсчитается отношение ординаты точки А на окружности к её абсциссе. Следовательно, если ctg α = b : а, а АС = sin θ, ОС = cos θ, то tgθ = sin θ : cos θ. Аналогично получаем ctg θ = cos θ : sin θ или 1 : tgθ.
Онлайн калькулятор расчета тангенса угла
Применение функции тангенса для решения задач
Что бы научиться пользоваться этой функцией, Нужно попробовать решить несколько примеров по применению этой функции.
Пример: есть два катета ВС = 7 см и АС = 12 см. Нам нужно узнать все остальные данные о треугольнике.
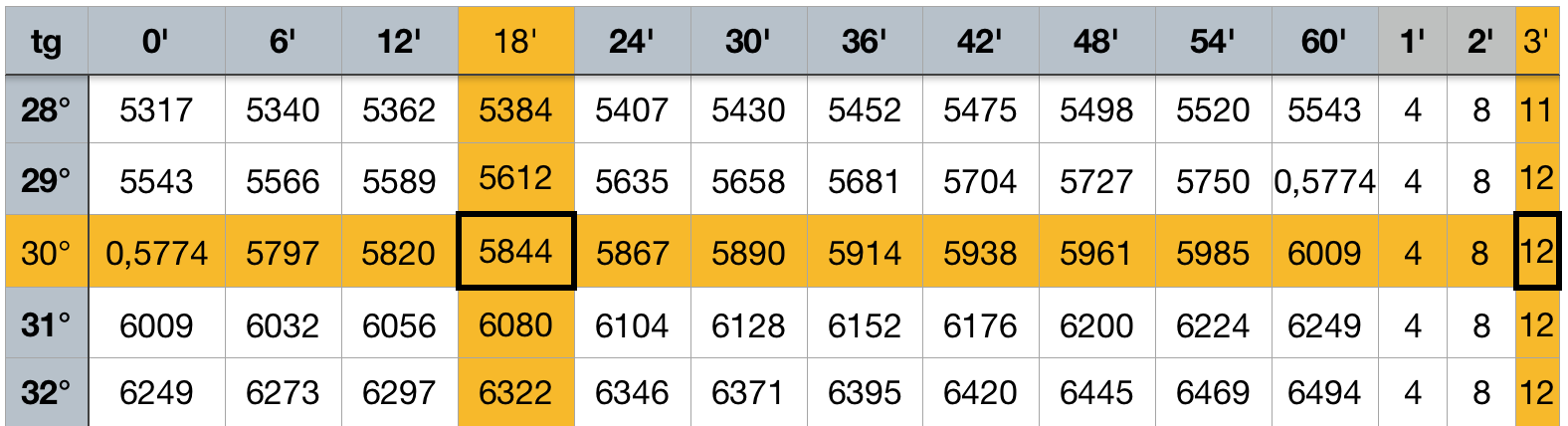
Первая формула, это tg α = а : b. тогда tg α = 7 :12= 0, 5833, далее для нахождения угла α используем таблицы Брадиса. На пересечении градусов и минут находим ближайшее значение угла – 0,5844, соответствующее 30° и 18′.
Находим ближайшую поправку, разную 3′. Отнимаем ее от нашего угла и получаем угол α = 30° 15′. Второй угол находим, исходя из того, что сумма всех углов должна быть не больше 180°, а угол γ = 90° по условию. Тогда угол β = 90° – 30° 15′= 59°45′.
Нам осталось найти гипотенузу с.
Можем найти её через sin α, который равен а: с, тогда с = а : sin α.
Находим sin α через таблицу Брадиса. Ближайшее значение 30° 36′, будет 0,5060, тогда не хватает 3′, Что по полям поправок равно 0,0008. Добавляем это число к найденному: 0, 5060 + 0,0008 = 0,5068. Подставляем это значение в формулу, с = 7:0,5068, с = 13, 8 см. Задача решена.
Можно искать значение углов через значение числа π, которое равно 180°. Тогда наиболее популярные углы, такие, как тангенс 30 градусов, тангенс 0 градусов, тангенс 60 градусов, тангенс 90 градусов, тангенс 45 градусов, тангенс 15 градусов, тангенс 75 градусов можно рассматривать намного проще. Нужно знать, что тангенс 0 градусов равен 0, а тангенс 90 градусов не имеет конкретного значения.
Можно найти тангенс угла 5 градусов, который равен 0, 0875 и добавлять или отнимать от наиболее часто встречающихся углов. Например угол 45 градусов, его тангенс равен 1, тогда тангенс угла 50 градусов будет равен 1, 0875. Тангенс 35 градусов можно рассчитать путем добавления к тангенсу 30 градусов угол 5 градусов, а тангенс 10 градусов это удвоение угла 5 градусов.
Для удобства есть рассчитанная таблица основных углов через значение π.
| Значение угла α (градусов) | Значение угла α в радианах | tg (тангенс) |
|---|---|---|
| Тангенс 0 | 0 | 0 |
| Тангенс 15 | π/12 | 0.2679 |
| Тангенс 30 | π/6 | 0.5774 |
| Тангенс 45 | π/4 | 1 |
| Тангенс 50 | 5π/18 | 5114 |
| Тангенс 60 | π/3 | 1.7321 |
| Тангенс 65 | 13π/36 | 2.1445 |
| Тангенс 70 | 7π/18 | 2.7475 |
| Тангенс 75 | 5π/12 | 3.7321 |
| Тангенс 90 | π/2 | — |
| Тангенс 105 | 5π/12 | -3.7321 |
| Тангенс 120 | 2π/3 | -1.7321 |
| Тангенс 135 | 3π/4 | -1 |
| Тангенс 140 | 7π/9 | -0.8391 |
| Тангенс 150 | 5π/6 | -0.5774 |
| Тангенс 180 | π | 0 |
| Тангенс 270 | 3π/2 | — |
| Тангенс 360 | 2π | 0 |
Если угол больше 90 градусов, нужно помнить, что функции имеют свойство повторяться, поэтому, если ищем тангенс 145 градусов, тогда 180 – 145 = 35 градусов, но уже со знаком «минус», это можно понять по чертежу окружности, где положительное или отрицательное значение абсциссы и ординаты. Научиться быстро пользоваться таблицами Брадиса и рассчитывать значения треугольника совсем не сложно, главное, уловить суть процесса.
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
Давайте докажем некоторые из них.
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
| 0 | |
| 0 | |
| 0 | |
| 0 | − |
| − | 0 |
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Ты нашел то, что искал? Поделись с друзьями!
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача решается за четыре секунды.
Найдем по теореме Пифагора.
Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.