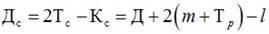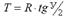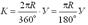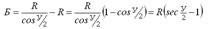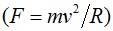Что называют тангенсом кривой
Тангенс кривой
Смотреть что такое «Тангенс кривой» в других словарях:
тангенс кривой — Отрезок прямой, соединяющий вершину угла поворота трассы с началом или концом кривой. [ГОСТ 22268 76] Тематики геодезия Обобщающие термины прикладная геодезия EN tangent DE Tangente FR tangente … Справочник технического переводчика
Тангенс кривой — 135. Тангенс кривой D. Tangente E. Tangent F. Tangente Отрезок прямой, соединяющий вершину угла поворота трассы с началом или концом кривой Источник: ГОСТ 22268 76: Геодезия. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
ТАНГЕНС — ТАНГЕНС, в ТРИГОНОМЕТРИИ ОТНОШЕНИЕ между длинами сторонами (катетов), противолежащей и прилежащей острому углу в прямоугольном ТРЕУГОЛЬНИКЕ (третья сторона гипотенуза). Выражение, обозначающее тангенс угла А, обычно сокращается до tg(A);… … Научно-технический энциклопедический словарь
ТАНГЕНС — (лат. tangens, от tangere касаться). Линия, касательная к окружности, т. е. прямая черта, коснувшаяся окружности или дуги в одной точке. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАНГЕНС в тригонометрии… … Словарь иностранных слов русского языка
ТАНГЕНС — см. Разбивка кривой. Технический железнодорожный словарь. М.: Государственное транспортное железнодорожное издательство. Н. Н. Васильев, О. Н. Исаакян, Н. О. Рогинский, Я. Б. Смолянский, В. А. Сокович, Т. С. Хачатуров. 1941 … Технический железнодорожный словарь
Касательная к кривой — График функции (чёрная кривая) и касательная прямая (красная прямая) Касательная прямая прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка. Содержание 1 Определение 2 Замечание … Википедия
ГОСТ 22268-76: Геодезия. Термины и определения — Терминология ГОСТ 22268 76: Геодезия. Термины и определения оригинал документа: 114. Абрис Ндп. Кроки D. Gelandeskizze Gelandekroki E. Outline Field sketch F. Croquis Схематический чертеж участка местности Определения термина из разных документов … Словарь-справочник терминов нормативно-технической документации
Модуль упругости (Е) — Modulus of elasticity Модуль упругости (Е). (1) Критерий жесткости материала; отношение напряжения вне предела пропорциональности к соответствующему напряжению. Если растягивающее напряжение 13,8 МПа приводит к удлинению на 1,0 %, модуль… … Словарь металлургических терминов
Дифференциальное исчисление — Исчисление бесконечно малых, включающее так называемое Д. исчисление, а также ему обратное интегральное, принадлежит к числу наиболее плодотворных открытий человеческого ума и составило эпоху в истории точных наук. Ближайшим поводом к изобретению … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Платежный баланс — (Balance of payments) Платежный баланс это статистический документ, отражающий все внешнеэкономические операции данной страны Платежный баланс страны, методы и структура составления платежного баланса, отрицательное и положительное сальдо… … Энциклопедия инвестора
Тангенс кривой
135. Тангенс кривой
Отрезок прямой, соединяющий вершину угла поворота трассы с началом или концом кривой
Смотреть что такое «Тангенс кривой» в других словарях:
тангенс кривой — Отрезок прямой, соединяющий вершину угла поворота трассы с началом или концом кривой. [ГОСТ 22268 76] Тематики геодезия Обобщающие термины прикладная геодезия EN tangent DE Tangente FR tangente … Справочник технического переводчика
Тангенс кривой — отрезок прямой от начала кривой в плане (конца кривой) до вершины угла поворота трассы. Источник: Справочник дорожных терминов … Строительный словарь
ТАНГЕНС — ТАНГЕНС, в ТРИГОНОМЕТРИИ ОТНОШЕНИЕ между длинами сторонами (катетов), противолежащей и прилежащей острому углу в прямоугольном ТРЕУГОЛЬНИКЕ (третья сторона гипотенуза). Выражение, обозначающее тангенс угла А, обычно сокращается до tg(A);… … Научно-технический энциклопедический словарь
ТАНГЕНС — (лат. tangens, от tangere касаться). Линия, касательная к окружности, т. е. прямая черта, коснувшаяся окружности или дуги в одной точке. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТАНГЕНС в тригонометрии… … Словарь иностранных слов русского языка
ТАНГЕНС — см. Разбивка кривой. Технический железнодорожный словарь. М.: Государственное транспортное железнодорожное издательство. Н. Н. Васильев, О. Н. Исаакян, Н. О. Рогинский, Я. Б. Смолянский, В. А. Сокович, Т. С. Хачатуров. 1941 … Технический железнодорожный словарь
Касательная к кривой — График функции (чёрная кривая) и касательная прямая (красная прямая) Касательная прямая прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка. Содержание 1 Определение 2 Замечание … Википедия
ГОСТ 22268-76: Геодезия. Термины и определения — Терминология ГОСТ 22268 76: Геодезия. Термины и определения оригинал документа: 114. Абрис Ндп. Кроки D. Gelandeskizze Gelandekroki E. Outline Field sketch F. Croquis Схематический чертеж участка местности Определения термина из разных документов … Словарь-справочник терминов нормативно-технической документации
Модуль упругости (Е) — Modulus of elasticity Модуль упругости (Е). (1) Критерий жесткости материала; отношение напряжения вне предела пропорциональности к соответствующему напряжению. Если растягивающее напряжение 13,8 МПа приводит к удлинению на 1,0 %, модуль… … Словарь металлургических терминов
Дифференциальное исчисление — Исчисление бесконечно малых, включающее так называемое Д. исчисление, а также ему обратное интегральное, принадлежит к числу наиболее плодотворных открытий человеческого ума и составило эпоху в истории точных наук. Ближайшим поводом к изобретению … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Платежный баланс — (Balance of payments) Платежный баланс это статистический документ, отражающий все внешнеэкономические операции данной страны Платежный баланс страны, методы и структура составления платежного баланса, отрицательное и положительное сальдо… … Энциклопедия инвестора
Основные элементы круговой кривой. Расчет
На всех линейных сооружениях, предназначенных для движения транспорта, в местах изменения направления трассы для сопряжения прямых участков с целью плавного и постепенного поворота движущего транспортного средства устраивают закругления или кривые. Закругления могут быть любыми. Простейшим является дуга окружности определенного радиуса, т.е. круговая кривая.
На железнодорожных дорогах применяют круговые кривые со следующими радиусами: 4000, 3000, 2000, 1800, 1500, 1200, 1000, 800, 700, 600, 400 и 300 м. Конкретное решение о применении радиусов железнодорожных кривых принимают в соответствии с конкретными условиями и строительно-техническими нормами СТН Ц-01-95.
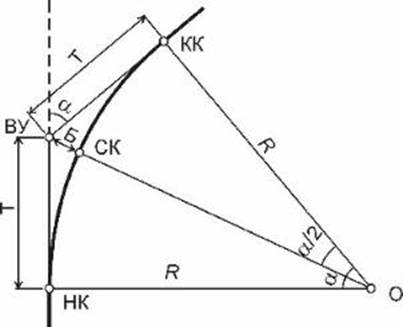
Круговая кривая характеризуется четырьмя главными точками и шестью основными элементами (рис. 83).
Главными точками кривой, которые определяют положение кривой на местности, являются: вершина угла ВУ; начало круговой кривой НКК; середина круговой кривой СКК; конец круговой кривой ККК.
Основными элементами кривой являются:
1. Угол поворота трассы У.
2. Радиус закругления R.
Во время изысканий угол У вычисляют, а радиус R назначают. Остальные элементы находят по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НКК, О (рис. 83).
3. Тангенс кривой (касательная) Т – расстояние по прямой от вершины угла до начала или конца кривой.
4. Длина кривой К от начала кривой до её конца.
5. Биссектриса кривой Б – отрезок от вершины угла до середины кривой.
6. Домер Д – разность между длиной двух тангенсов и кривой.
Все элементы кривой можно вычислить по вышеприведенным формулам. Но так как Т, K, Б и Д находятся в прямой зависимости от угла поворота и радиуса, то для их определения составлены специальные таблицы для разбивки кривых.
Вычислить пикетажные значения главных точек кривой – значит узнать на каких пикетах и плюсовых точках они находятся.
Сначала определяют пикетаж вершины угла поворота ВУ, а затем находят пикетажное значение начала, конца и середины кривой
.
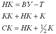
Круговые и переходные кривые.
Главными точками кривой, определяющими её положение на местности, являются вершина угла ВУ, начало кривой НК, середина кривой СК и конец кривой КК (рис. 15.3).
Рис. 15.3 Схема круговой кривой
Основные элементы кривой – её радиус R и угол поворота a. К основным элементам относятся также:
Во время изысканий угол a измеряют, а радиус R назначают. Остальные элементы вычисляют по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НК, О (центр окружности):
Домер вычисляют по формуле
. (15.2)
Вместо вычислений по формулам можно воспользоваться таблицами для разбивки кривых на железных дорогах, где по заданным радиусу и углу поворота сразу находят значения Т, К, Б и Д.
В месте поворота трассы пикетаж ведётся по кривой. Пикетажное положение главных точек кривой определяют по формулам:
Правильность вычислений контролируют по формулам:
Измерено a = 18°19¢ и задан радиус R = 600 м. Вершина угла расположена на пикете 6 + 36,00.
По формулам (15.1) и (15.2) или по таблицам находим элементы кривой: Т = 96,73 м; К = 191,81 м; Д = 1,65 м; Б = 7,75 м.
Вычислим пикетажное положение главных точек:
ПК ВУ 6 + 36,00 ПК ВУ 6 + 36,00
ПК НК 5 + 39,27 7 + 32,73
ПК КК 7 + 31,08 ПК КК 7 + 31,08
ПК НК 5 + 39,27 ПК ВУ 6 + 36,00
ПК СК 6 + 35,17 ПК СК 6 + 35,18
Переходные кривые. Непосредственное сопряжение прямого участка пути с круговой кривой приводит к тому, что во время движения поезда в месте сопряжения внезапно возникает центробежная сила F, прямо пропорциональная квадрату скорости движения v и обратно пропорциональная радиусу кривой 
. Чтобы обеспечить постепенное нарастание центробежной силы, между прямой и круговой кривой вставляют переходную кривую, радиус кривизны r которой плавно изменяется от ¥ до R. Если положить, чтобы центробежная сила менялась пропорционально расстоянию s от начала кривой, то получим
,
R – радиус кривизны в конце переходной кривой.
Индексом k отмечены значения переменных в конце переходной кривой.
Для радиуса кривизны переходной кривой в текущей точке i найдём:
где через l обозначена длина переходной кривой sk. Кривая, описываемая уравнением (15.5), в математике называется клотоидой, или радиоидальной спиралью.
Угол поворота трассы на переходной кривой. На бесконечно малом отрезке кривой ds (рис. 15.4, а) происходит поворот трассы на угол
.
Подставляя выражение радиуса кривизны r из (15.5), получим
.
Выполним интегрирование от начала кривой НК, где j = 0 и s = 0, до текущей точки i:
,
Рис. 15.4 Схема переходной кривой:
а – углы поворота трассы: φ – в текущей точке i, β – в конце
Из полученного уравнения вытекают формулы:
; 
; l = 2Rb, (15.6)
Координаты точки переходной кривой. Совместим начало координат с началом переходной кривой и направим ось x по касательной к ней (см. рис. 15.4, а). Бесконечно малому приращению дуги кривой соответствуют бесконечно малые приращения координат (рис. 15.4, б):
Разложим синус и косинус в ряд и, удержав в разложениях по два члена, подставим в них выражения для j из (15.6):
Подставляя полученные выражения в (15.7) и выполняя интегрирование, найдём:
; (15.8)
. (15.9)
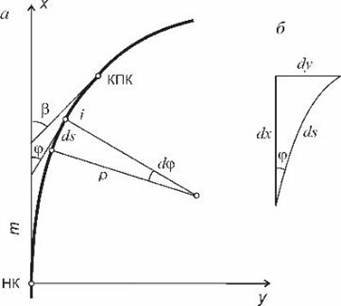
Смещение начала кривой (сдвижка). На рис. 15.5 дуга НК-КПК представляет собой переходную кривую, переходящую после точки КПК в круговую. Продолжим круговую кривую до точки Q, где её направление, параллельно оси x. Обозначим через m смещение, параллельное оси x, начала переходной кривой относительно точки Q, в которой начиналась бы круговая кривая при отсутствии переходной. Через p обозначим смещение в перпендикулярном направлении. Из рис. 15.5 видно:
,
Сочетание круговой кривой с переходными. На рис. 15.6 показана кривая, поворачивающая трассу на угол a и состоящая из круговой части с радиусом R и двух переходных кривых одинаковой длины l.
Рис. 15. 5 Смещение начала переходной кривой
Рис. 15.6 Сопряжение круговой кривой
Если бы не было переходных кривых, в образованный прямыми линиями трассы угол была бы вписана дуга окружности радиуса R, равная Q-СК-Q1 и имеющая длину K = Ra.
При наличии переходных кривых на каждой из них происходит поворот трассы на угол b, отчего на долю круговой кривой приходится поворот на угол a-2b. Поэтому суммарная длина кривой равна
Тангенс и биссектриса определяются по формулам:
Домер в этом случае равен
.
В полевых условиях значения m, Тp и Бp вычисляют на микрокалькуляторе или выбирают из таблиц для разбивки кривых на железных дорогах. Пикетажное положение главных точек кривой вычисляют по формулам, аналогичным (15.3) и (15.4).
Что называют тангенсом кривой
Радиус кривой выбирают при проектировании дороги, руководствуясь конкретными техническими условиями. Главными точками кривой, определяющими её положение на местности, являются вершина угла ВУ, начало кривой НК, середина кривой СК и конец кривой КК рис. 2.3.
Основные элементы кривой – её радиус R и угол поворота a. К основным элементам относятся также:
Во время изысканий угол a измеряют, а радиус R назначают. Остальные элементы вычисляют по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НК, О (центр окружности):
Домер вычисляют по формуле
Вместо вычислений по формулам можно воспользоваться таблицами для разбивки кривых на железных дорогах, где по заданным радиусу и углу поворота сразу находят значения Т, К, Б и Д.
В месте поворота трассы пикетаж ведётся по кривой. Пикетажное положение главных точек кривой определяют по формулам:
ПК СК = ПК НК + К/2. (2.3.)
Правильность вычислений контролируют по формулам:
ПК СК = ПК ВУ + Д/2. (2.4.)
Непосредственное сопряжение прямого участка пути с круговой кривой приводит к тому, что во время движения поезда в месте сопряжения внезапно возникает центробежная сила F, прямо пропорциональная квадрату скорости движения v и обратно пропорциональная радиусу кривой
Чтобы обеспечить постепенное нарастание центробежной силы, между прямой и круговой кривой вставляют переходную кривую, радиус кривизны r которой плавно изменяется от ∞ до R. Если положить, чтобы центробежная сила менялась пропорционально расстоянию s от начала кривой, то получим
(2.5.)
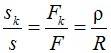
R – радиус кривизны в конце переходной кривой.
Индексом k отмечены значения переменных в конце переходной кривой.
Для радиуса кривизны переходной кривой в текущей точке i найдём:
где через l обозначена длина переходной кривой S k.
Кривая, описываемая уравнением (2.6.), в математике называется клотоидой, или радиоидальной спиралью. Угол поворота трассы на переходной кривой. На бесконечно малом отрезке кривой ds (рис. 2.4.) происходит поворот трассы на угол
(2.7.)
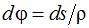
Подставляя выражение радиуса кривизны r из (2.5.), получим
(2.6.)
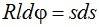
Выполним интегрирование от начала кривой НК, где j = 0 и s = 0, до текущей точки i:
(2.7),
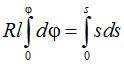
Из полученного уравнения вытекают формулы:
; 
;
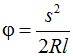
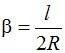
Совместим начало координат с началом переходной кривой и направим ось x по касательной к ней (см. рис. 2.4.). Бесконечно малому приращению дуги кривой соответствуют бесконечно малые приращения координат (рис. 2.4.):
Разложим синус и косинус в ряд и, удержав в разложениях по два члена, подставим в них выражения для j:
Подставляя полученные выражения и выполняя интегрирование, найдём:
; (2.12.)
(2.13.)
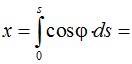
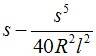
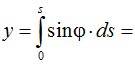
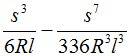
Смещение начала кривой (сдвижка). На рис. 2.5. дуга НК-КПК представляет собой переходную кривую, переходящую после точки КПК в круговую. Продолжим круговую кривую до точки Q, где её направление, параллельно оси x. Обозначим через m смещение, параллельное оси x, начала переходной кривой относительно точки Q, в которой начиналась бы круговая кривая при отсутствии переходной. Через p обозначим смещение в перпендикулярном направлении. Из рис. 2.5. видно:
(2.14.)
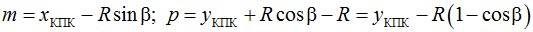
Сочетание круговой кривой с переходными. На рис. 2.6. показана кривая, поворачивающая трассу на угол a и состоящая из круговой части с радиусом R и двух переходных кривых одинаковой длины l.
Если бы не было переходных кривых, в образованный прямыми линиями трассы угол была бы вписана дуга окружности радиуса R, равная Q-СК-Q1 и имеющая длину K = Ra.
При наличии переходных кривых на каждой из них происходит поворот трассы на угол b, отчего на долю круговой кривой приходится поворот на угол a-2b. Поэтому суммарная длина кривой равна
Тангенс и биссектриса определяются по формулам:
Тс = T + m + Tp; Бc = Б + Бp (2.16)
где Т p = ptg(a/2); Б p = psec(a/2).
Домер в этом случае равен
(2.17.)