Что называют сторонами треугольника
Треугольник
Треугольник — это замкнутая ломаная линия, состоящая из трёх звеньев:
Вершины ломаной называются вершинами треугольника, а её звенья — сторонами треугольника. Углы, образованные двумя сторона треугольника, называются углами треугольника:
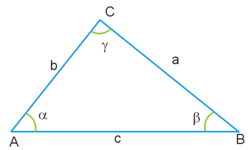
В треугольнике ABC вершины A, B и C — это вершины треугольника, звенья AB, BC и CA — стороны треугольника. Три угла — ∠ABC, ∠BCA и ∠CAB — углы треугольника. Часто углы треугольника обозначаются только одной буквой: ∠A, ∠B, ∠C.
У каждого треугольника 3 вершины, 3 стороны и 3 угла.
Высота
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его основание. Высота треугольника может быть опущена и на продолжение основания.
Отрезок BN — это высота 
ABC. Отрезок EL высота DEF, опущенная на продолжение стороны DF.
Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.
Каждый треугольник имеет три высоты.
Биссектриса
Биссектриса угла треугольника — прямая, делящая угол треугольника пополам. Длина отрезка этой прямой от вершины угла до точки пересечения с противоположной стороной называется длиной биссектрисы.
Отрезок BN — это биссектриса ABC.
Каждый треугольник имеет три биссектрисы.
Медиана
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Длина этого отрезка называется длиной медианы.
Отрезок BN — это медиана ABC.
Треугольник
Треуго́льник (в евклидовом пространстве) — это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника. Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла. Если три точки лежат на одной прямой, то «треугольник» с вершинами в трёх данных точках называется вырожденным. Все остальные треугольники невырожденные.
В неевклидовых пространствах в качестве сторон треугольника выступают геодезические линии, которые, как правило, являются криволинейными. Поэтому такие треугольники называют криволинейными.
Содержание
Элементы треугольника
Треугольник с вершинами A, B и C обозначается как 
(см. рис.). Треугольник имеет три стороны:
Длины сторон треугольника обозначаются строчными латинскими буквами (a, b, c):
Треугольник имеет следующие углы:
Величины углов при соответствующих вершинах традиционно обозначаются греческими буквами (α, β, γ).
Признаки равенства треугольников
Треугольник на евклидовой плоскости однозначно (с точностью до конгруэнтности) можно определить по следующим тройкам основных элементов:
Признаки равенства прямоугольных треугольников:
В сферической геометрии и в геометрии Лобачевского существует признак равенства треугольников по трём углам.
Типы треугольников
| Типы треугольников | ||
|---|---|---|
| Файл:Triangle-acute.svg Остроугольный | Файл:Triangle-obtuse.svg Тупоугольный | 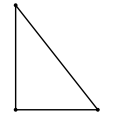 Прямоугольный |
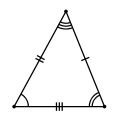 Разносторонний | Файл:Triangle-isosceles.svg Равнобедренный | 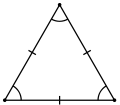 Равносторонний |
По величине углов
Поскольку в евклидовой геометрии сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми (меньшими 90°). Выделяют следующие виды треугольников:
В геометрии Лобачевского сумма углов треугольника всегда меньше 180°, а на сфере — всегда больше. Разность суммы углов треугольника и 180° называется дефектом. Дефект пропорционален площади треугольника, таким образом, у бесконечно малых треугольников на сфере или плоскости Лобачевского сумма углов будет мало отличаться от 180°.
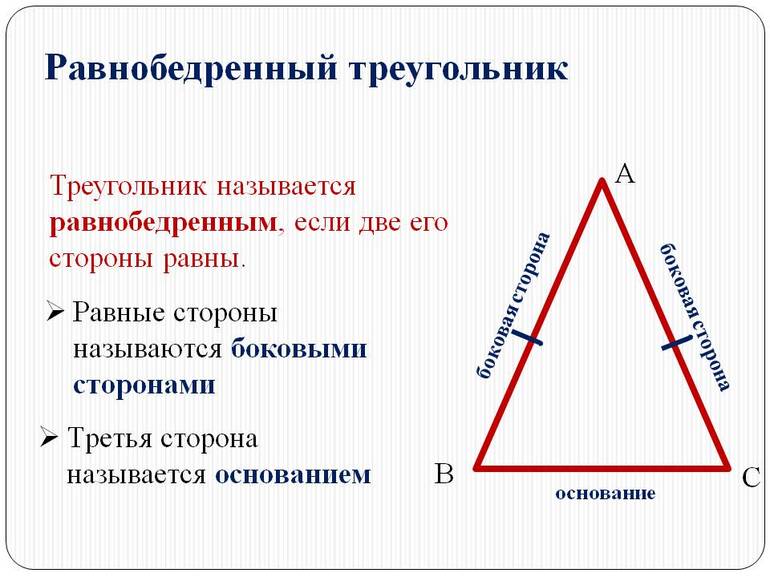
По числу равных сторон
Определения, связанные с треугольником
Все факты, изложенные в этом разделе, из евклидовой геометрии.
Лучи, отрезки и точки
В равнобедренном треугольнике медиана, высота и биссектриса, проведённые к основанию, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведённые из одной вершины, совпадают, то треугольник равнобедренный. Если треугольник разносторонний, то для любой его вершины биссектриса, проведённая из неё, лежит между медианой и высотой, проведёнными из той же вершины.
Чевианы, лежащие на прямых, симметричных медианам относительно биссектрис, называются симедианами. Они проходят через одну точку — точку Лемуана.
Некоторые точки в треугольнике — «парные». Например, существует две точки, из которых все стороны видны либо под углом в 60°, либо под углом в 120°. Они называются точками Торричелли. Также существует две точки, проекции которых на стороны лежат в вершинах правильного треугольника. Это — точки Аполлония. Точки 
и 
такие, что 
и 
называются точками Брокара.
Прямые
В любом треугольнике центр тяжести, ортоцентр и центр описанной окружности лежат на одной прямой, называемой прямой Эйлера.
Прямая, проходящая через центр описанной окружности и точку Лемуана, называется осью Брокара. На ней лежат точки Аполлония. Также на одной прямой лежат точки Торричелли и точка Лемуана. Основания внешних биссектрис углов треугольника лежат на одной прямой, называемой осью внешних биссектрис. На одной прямой лежат также точки пересечения прямых, содержащих стороны ортотреугольника, с прямыми, содержащими стороны треугольника. Эта прямая называется ортоцентрической осью, она перпендикулярна прямой Эйлера.
Если на описанной окружности треугольника взять точку, то её проекции на стороны треугольника будут лежать на одной прямой, называемой прямой Симсона данной точки. Прямые Симсона диаметрально противоположных точек перпендикулярны.
Треугольники
Окружности
Середины трёх сторон треугольника, основания трёх его высот и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности, называемой окружностью девяти точек или окружностью Эйлера. Центр окружности девяти точек лежит на прямой Эйлера. Окружность девяти точек касается вписанной окружности и трёх вневписанных. Точка касания вписанной окружности и окружности девяти точек называется точкой Фейербаха. Если от каждой вершины отложить наружу треугольника на прямых, содержащих стороны, ортезки, равные по длине противоположным сторонам, то получившиеся шесть точек лежат на одной окружности — окружности Конвея. В любой треугольник можно вписать три окружности таким образом, что каждая из них касается двух сторон треугольника и двух других окружностей. Такие окружности называются окружностями Мальфатти. Центры описанных окружностей шести треугольников, на которые треугольник разбивается медианами, лежат на одной окружности, которая называется окружностью Ламуна.
В треугольнике есть три окружности, которые касаются двух сторон треугольника и описанной окружности. Такие окружности называют полувписанными или окружностями Веррьера. Отрезки, соединяющие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке, называемой точкой Веррьера. Она служит центром гомотетии, которая переводит описанную окружность во вписанную. Точки касания окружностей Веррьера со сторонами лежат на прямой, которая проходит через центр вписанной окружности.
Отрезки, соединяющие точки касания вписанной окружности с вершинами, пересекаются в одной точке, называемой точкой Жергонна, а отрезки, соединяющие вершины с точками касания вневписанных окружностей — в точке Нагеля.
Эллипсы, параболы и гиперболы
В треугольник можно вписать бесконечно много коник (эллипсов, парабол или гипербол). Если в треугольник вписать произвольную конику и соединить точки касания с противоположными вершинами, то получившиеся прямые пересекутся в одной точке, называемой перспектором коники. Для любой точки плоскости, не лежащей на стороне или на её продолжении существует вписанная коника с перспектором в этой точке. [1]
В треугольник можно вписать эллипс, который касается сторон в серединах. Такой эллипс называется вписанным эллипсом Штейнера (его перспектором будет центроид треугольника). [2] Описанный эллипс, который касается прямых, проходящих через вершины параллельно сторонам, называется описанным эллипсом Штейнера. Если аффинным преобразованием («перекосом») перевести треугольник в правильный, то его вписанный и описанный эллипс Штейнера перейдут во вписанную и описанную окружности. Чевианы, проведённые через фокусы описанного эллипса Штейнера (точки Скутина), равны (теорема Скутина). Изо всех описанных эллипсов описанный эллипс Штейнера имеет наименьшую площадь, а изо всех вписанных наибольшую площадь имеет вписанный эллипс Штейнера. [3]
Эллипс с фокусами в точках Брокара называется эллипсом Брокара. Его перспектором служит точка Лемуана. [4]
Перспекторы вписанных парабол лежат на описанном эллипсе Штейнера. [5] Фокус вписанной параболы лежит на описанной окружности, а директриса проходит через ортоцентр. [6] Парабола, вписанная в треугольник, имеющая директрисой прямую Эйлера, называется параболой Киперта. Её перспектор — четвёртая точка пересечения описанной окружности и описанного эллипса Штейнера, называемая точкой Штейнера.
Если описанная гипербола проходит через точку пересечения высот, то она равносторонняя (то есть её асимптоты перпендикулярны). [7] Точка пересечения асимптот равносторонней гиперболы лежит на окружности девяти точек. [7]
Преобразования
Если прямые, проходящие через вершины и некоторую точку, не лежащую на сторонах и их продолжениях, отразить относительно соответствующих биссектрис, то их образы также пересекутся в одной точке, которая называется изогонально сопряжённой исходной (если точка лежала на описанной окружности, то получившиеся прямые будут параллельны). Изогонально сопряжёнными являются многие пары замечательных точек: центр описанной окружности и ортоцентр, центроид и точка Лемуана, точки Брокара. Точки Аполлония изогонально сопряжены точкам Торричелли, а центр вписанной окружности изогонально сопряжён сам себе. Под действием изогонального сопряжения прямые переходят в описанные коники, а описанные коники — в прямые. Так, изогонально сопряжены гипербола Киперта и ось Брокара, гипербола Енжабека и прямая Эйлера, гипербола Фейербаха и линия центров вписанной о описанной окружностей. Описанные окружности подерных треугольников изогонально сопряжённых точек совпадают. Фокусы вписанных эллипсов изогонально сопряжены.
Если вместо симметричной чевианы брать чевиану, основание которой удалено от середины стороны так же, как и основание исходной, то такие чевианы также пересекутся в одной точке. Получившееся преобразование называется изотомическим сопряжением. Оно также переводит прямые в описанные коники. Изотомически сопряжены точки Жергонна и Нагеля. При аффинных преобразованиях изотомически сопряжённые точки переходят в изотомически сопряжённые. При изотомическом сопряжении в бесконечно удалённую прямую перейдёт описанный эллипс Штейнера.
Если в сегменты, отсекаемые сторонами треугольника от описанного круга, вписать окружности, касающиеся сторон в основаниях чевиан, проведённых через некоторую точку, а затем соединить точки касания этих окружностей с описанной окружностью с противоположными вершинами, то такие прямые пересекутся в одной точке. Преобразование плоскости, сопоставляющее исходной точке получившуюся, называется изоциркулярным преобразованием. Композиция изогонального и изотомического сопряжений является композицией изоциркулярного преобразования с самим собой. Эта композиция — проективное преобразование, которое стороны треугольника оставляет на месте, а ось внешних биссектрис переводит в бесконечно удалённую прямую.
Если продолжить стороны чевианного треугольника некоторой точки и взять их точки пересечения с соответствующими сторонами, то полученные точки пересечения будут лежать на одной прямой, называемой трилинейной полярой исходной точки. Ортоцентрическая ось — трилинейная поляра ортоцентра; трилинейной полярой центра вписанной окружности служит ось внешних биссектрис. Трилинейные поляры точек, лежищих на описанной конике, пересекаются в одной точке (для описанной окружности это точка Лемуана, для описанного эллипса Штейнера — центроид). Композиция изогонального (или изотомического) сопряжения и трилинейной поляры является преобразованием двойственности (если точка, изогонально (изотомически) сопряжённая точке 
, лежит на трилинейной поляре точки 
, то трилинейная поляра точки, изогонально (изотомически) сопряжённой точке лежит на трилинейной поляре точки ).
Кубики
Кубика — это кривая третьего порядка (задающаяся уравнением третьей степени). Многие замечательные кубики, связанные с треугольником, строятся следующим образом: фиксируется точка в плоскости (возможно, бесконечно удалённая). Тогда множество таких точек , что прямая 
проходит через эту точку, является описанной около треугольника кубикой (здесь 
— точка, изогонально сопряжённая ). Такие кубики проходят также через центры вписанной и вневписанных окружностей, а также через саму фиксированную точку и изогонально сопряжённую ей. [10]
Соотношения в треугольнике
Примечание: в данном разделе 
, 
, 
— это длины трёх сторон треугольника, и 
, 
, 
— это углы, лежащие соответственно напротив этих трёх сторон (противолежащие углы).
Неравенство треугольника
В невырожденном треугольнике сумма длин двух его сторон больше длины третьей стороны, в вырожденном — равна. Иначе говоря, длины сторон треугольника связаны следующими неравенствами:
Неравенство треугольника является одной из аксиом метрики.
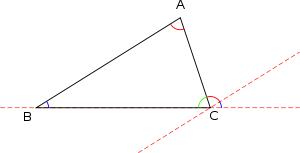
Теорема о сумме углов треугольника
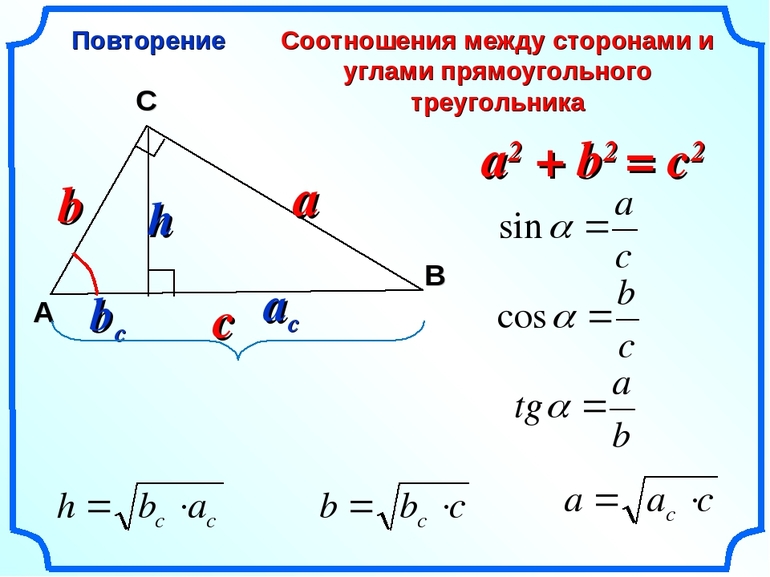
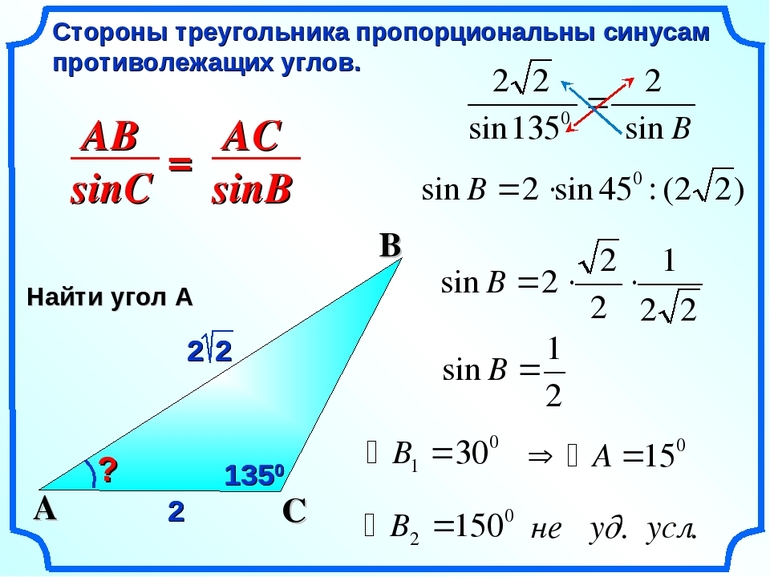
Теорема синусов
где R — радиус окружности, описанной вокруг треугольника. Из теоремы следует, что если a Теорема косинусов
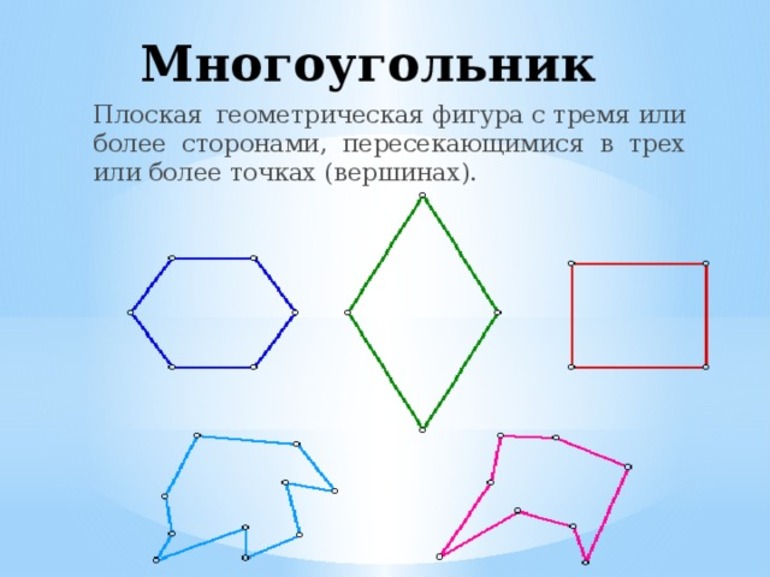
Многоугольник с тремя сторонами
Прежде чем рассматривать задачу о том, как проверить, существует ли треугольник, следует подробно изучить эту фигуру. Согласно общепринятому определению, любой замкнутый многоугольник на плоскости, который состоит из трех отрезков, пересекающихся своими концами друг с другом, является треугольником. Эта фигура имеет две группы образующих ее элементов:
Сторонами являются три отрезка, длины которых могут быть либо известны по условию задачи, либо их предстоит рассчитать. Касательно вершин следует сказать, что у любого рассматриваемого многоугольника их три. Каждую принято обозначать одной латинской буквой, например, A, B, C и так далее. Поскольку два отрезка пересекаются в вершине, то они образуют некоторый угол. Их у фигуры три, поэтому становится понятным, откуда происходит название «треугольник».
Типы фигуры
Их классификация является достаточно развитой. В ее основу положены принципы взаимоотношения длин сторон друг с другом, а также численные значения углов. В общем случае в геометрии рассматривают следующие типы треугольников:
Два основных свойства
В некоторых геометрических задачах можно встретить проблемы, которые формулируются так: можно ли построить треугольник со сторонами a, b, c, если известны их длины. Либо другой тип задач, которые предполагают знание некоторых сторон и углов, и требуют определить возможность существования такой фигуры.
Ответ на все эти проблемы заключается всего в одном слове: либо «да» и такой треугольник действительно существует, либо «нет» и из заданных элементов его построить не представляется возможным. Разобраться со всеми этими задачами поможет знание двух главных свойств, которые всегда справедливы для треугольников любых типов:
Оба свойства с успехом можно и необходимо применять, чтобы проверить или узнать возможность существования того или иного треугольника. Важно понимать, что невыполнение любого из свойств говорит о невозможности построения рассматриваемой фигуры.
Вопрос вырождения
В свете изучения возможности существования треугольников важно рассмотреть вопрос их вырождения. В математике придумали универсальную формулу, которая позволяет оценить качество треугольника. Она имеет вид:
Каждый из трех множителей числителя является положительным числом, что следует из главного свойства треугольников. Величина качества CT является положительной и лежит в пределах значений 0 и 1. Возможны следующие случаи:
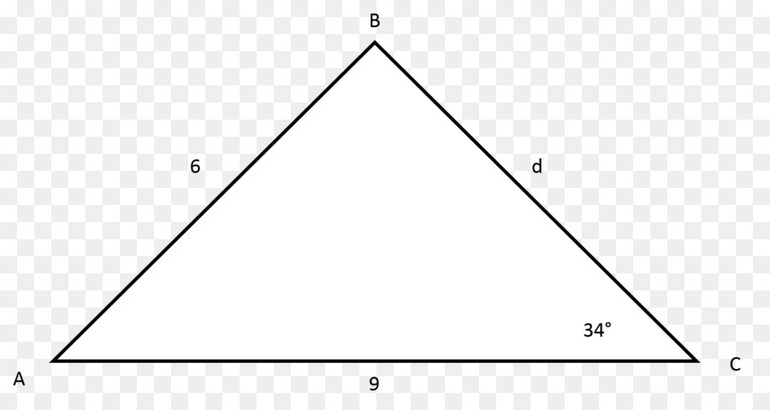
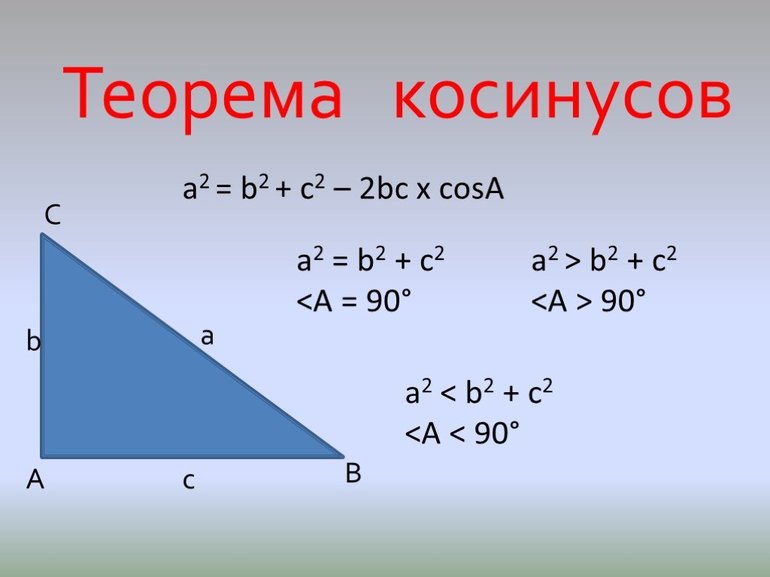
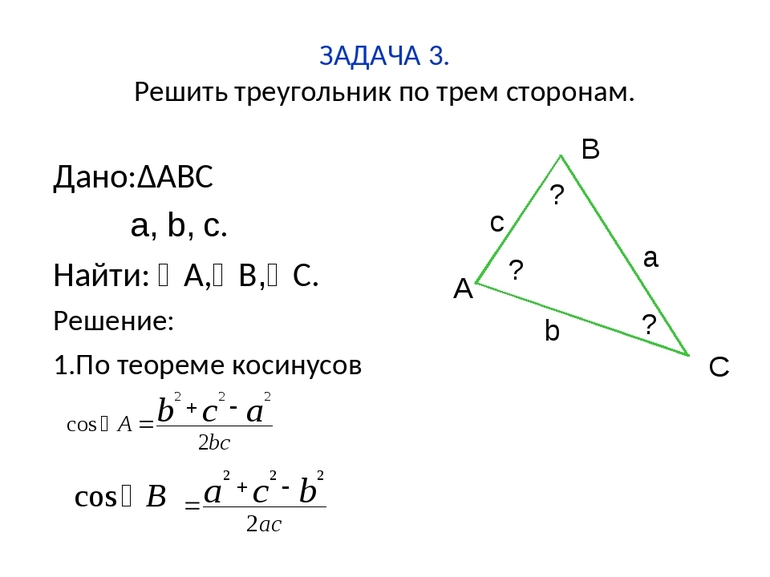
Теорема косинусов
Чтобы решать задачи на треугольники, недостаточно знать лишь главные их свойства. Последние позволяют лишь дать качественный, но не количественный ответ. Теорем и формул для рассматриваемых многоугольников известно много (синусов, Пифагора, медиан, Герона и др.). Однако, теорема косинусов является одной из основополагающих, поскольку позволяет по двум сторонам и углу определить значение длины третьей стороны (справедливости ради следует отметить, что теорема синусов является не менее важной, поскольку она по двум углам и стороне позволяет вычислить неизвестные стороны).
Соответствующее выражение имеет следующий вид:
c 2 = a 2 + b 2 — 2*a*b*cos (α).
Решение задач
Для закрепления полученных знаний полезно привести пару примеров решения типичных геометрических задач с треугольниками, в которых нужно будет либо дать качественный ответ, либо получить некоторое количественное значение.
Первая задача требует получить качественный ответ. Пусть имеется треугольник со сторонами 1, 2, 4. Существует ли такая фигура, требуется выяснить.
Для решения этой проблемы абсолютно неважно измеряются стороны в метрах, в сантиметрах, в дюймах или в других величинах. Важно лишь взаимоотношение между ними. Для каждой из длин отрезков следует проверить свойство существования рассматриваемой фигуры. Если получится хотя бы одна ложь, то треугольник построить нельзя:
Таким образом, для определения возможности существования того или иного треугольника на плоскости необходимо проверить тот факт, что каждая из его сторон имеет меньшую длину, чем сумма двух других отрезков. Теорема косинусов является удобным инструментом для определения количественных характеристик рассматриваемого типа фигур.