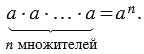Что называют степенью числа а с натуральным показателем n большим 1

Степень числа. Квадрат и куб числа

Определение.

Степенью числа «» с натуральным показателем ««, большим 1, называется произведение «» одинаковых множителей, каждый из которых равен числу ««.

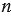
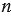
Например, найдем значение следующих степеней:

2 4 = 2222 = 422 = 82 = 16;

3 6 = 333333 = 93333 = 27333 = 8133 =2433 = 729.

Например, найдем квадрат чисел 4 и 8:

4 2 = 44 = 16;

8 2 = 88 = 64.

Например, найдем куб чисел 5 и 7:

5 3 = 555 = 255 = 125;

7 3 = 777 = 495 = 343;

Степенью числа «» с показателем = 1 является само это число, то есть .

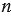
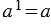
Сначала выполним возведение во 2 степень числа 4, затем находим значение выражения, находящегося в скобках, после чего выполняем умножение, и последним действием выполняем вычитание:

Поделись с друзьями в социальных сетях:

Источник

Степень с натуральным показателем и её свойства

Степень с натуральным показателем.

Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен a:

a n =

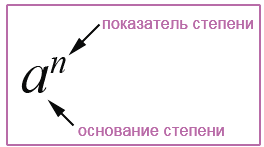
— число а (повторяющийся множитель) называют основанием степени

— число n (показывающее сколько раз повторяется множитель) – показателем степени

Например:
2 5 = 2·2·2·2·2 = 32,
здесь:
2 – основание степени,
5 – показатель степени,
32 – значение степени

Отметим, что основание степени может быть любым числом.

Вычисление значения степени называют действием возведения в степень. Это действие третьей ступени. То есть при вычислении значения выражения, не содержащего скобки, сначала выполняют действие третьей ступени, затем второй (умножение и деление) и, наконец, первой (сложение и вычитание).

Для записи больших чисел часто применяются степени числа 10. Так, расстояние от земли до солнца примерно равное 150 млн. км, записывают в виде 1,5 · 10 8

Свойства степени с натуральным показателем:

a m · a n = a m + n

a m / a n = a m — n ,

где, m > n,
a ≠ 0

(a m ) n = a m · n

например: (2 3 ) 2 = 2 3·2 = 2 6

(a / b) n = a n / b n

например: (2 / 5) 3 =(2 / 5)·(2 / 5)·(2 / 5) = 2 3 /5 3

Степень с рациональным показателем

Степенью числа а > 0 с рациональным показателем , где m – целое число, а n – натуральное (n > 1), называется число

Итак:

Например:

Степень числа 0 определена только для положительных показателей;

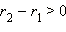
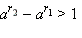
Но и потому (так как a > 1) и, наконец,

Источник

Числа. Степень числа.

То есть вместо умножения шести одинаковых множителей 5х5х5х5х5х5 пишут 5 6 и говорят «пять в шестой степени».

Действия, с помощью которых произведение равных множителей сворачивают в степень, называют возведением в степень.

В общем виде степень с основанием «a» и показателем «n» записывается так

Возвести число a в степень n – значит найти произведение n множителей, каждый из которых равен а

Если основание степени «а» равно 1, то значение степени при любом натуральном n будет равно 1. Например, 1 5 =1, 1 256 =1

Если возвести число «а» возвести в первую степень, то получим само число a: a 1 = a

Особыми считают вторую и третью степень числа. Для них придумали названия: вторую степень называют квадратом числа, третью – кубом этого числа.

-при нахождении степени положительного числа получается положительное число.

-при вычислениях нуля в натуральной степени получаем ноль.

— при вычислении степени отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Если решить несколько примеров на вычисление степени отрицательных чисел, то получится, что если мы вычисляем нечётную степень отрицательного числа, то в результате будет число со знаком минус. Так как при умножении нечётного количество отрицательных сомножителей получаем отрицательное значение.

Если же мы рассчитываем четную степень для отрицательного числа, то в результате будет положительное число. Так как при умножении чётного количества отрицательных сомножителей получаем положительное значение.

Свойства степени с натуральным показателем.

Чтобы умножить степени с одинаковыми основаниями мы основания не меняем, а показатели степеней складываем:

Чтобы разделить степени с одинаковыми основаниями основание не меняем, а показатели степеней вычитаем:

При расчетах возведения степени в степень основание не меняем, а показатели степеней умножаем друг на друга.

например: (2 3 ) 2 = 2 3·2 = 2 6

Если необходимо рассчитать возведение в степень произведения, то в эту степень возводится каждый множитель

При выполнении расчетов по возведению в степень дроби мы в данную степень возводим числитель и знаменатель дроби

Последовательность выполнения расчетов при работе с выражениями содержащими степень.

При выполнении расчетов выражений без скобок, но содержащих степени, в первую очередь производят возведение в степень, потом действия умножение и деление, и лишь потом операции сложения и вычитания.

Если необходимо вычислить выражение содержащие скобки, то сначала в указанном выше порядке делаем вычисления в скобках, а потом оставшиеся действия в том же порядке слева направо.

Очень широко в практических вычислениях для упрощения расчетов используют готовые таблицы степеней.

Источник

Что такое степень числа

Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулём.

Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.

Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

Вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 4 6 и произносят «четыре в шестой степени».

4 · 4 · 4 · 4 · 4 · 4 = 4 6

Выражение 4 6 называют степенью числа, где:

В общем виде степень с основанием « a » и показателем « n » записывается с помощью выражения:

Исключение составляют записи:

Конечно, выражения выше можно читать и по определению степени:

Степенью числа « а » с показателем n = 1 является само это число:
a 1 = a

Любое число в нулевой степени равно единице.
a 0 = 1

Ноль в любой натуральной степени равен нулю.
0 n = 0

Единица в любой степени равна 1.
1 n = 1

Выражение 0 0 (ноль в нулевой степени) считают лишённым смысла.

При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.

Пример. Возвести в степень.

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.

При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

Квадрат любого числа есть положительное число или нуль, то есть:

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (−5) 4 и −5 4 это разные выражения. Результаты возведения в степень данных выражений будут разные.

Вычислить (−5) 4 означает найти значение четвёртой степени отрицательного числа.

В то время как найти « −5 4 » означает, что пример нужно решать в 2 действия:

Пример. Вычислить: −6 2 − (−1) 4

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Для облегчения решения примеров полезно знать и пользоваться таблицей степеней, которую вы можете бесплатно скачать на нашем сайте.

Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором «Возведение в степень онлайн».

Источник

Алгебра. 7 класс

Конспект урока

Перечень вопросов, рассматриваемых в теме:

Понятие степени числа.

Степенью числа a с натуральным показателем n, бóльшим 1, называется произведение n одинаковых множителей, каждый из которых равен числу a.

Произведение степеней с одним и тем же показателем равно степени с тем же показателем и основанием, равным произведению оснований.

Произведение степеней с одним и тем же основанием – это степень с тем же основанием и показателем, равным сумме показателей этих степеней.

Степень степени числа равна степени того же числа с показателем, равным произведению показателей этих степеней.

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

1. Макарычев Ю. Н. Алгебра: 7 класс. // Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. – М.: Просвещение, 2019. – 256 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

При этом число 8 называют основанием степени, а число 6 – показателем степени.

А теперь давайте сформулируем общее определение степени числа, опираясь на предыдущий пример:

степенью числа a с натуральным показателем n, бóльшим 1, называется произведение n одинаковых множителей, каждый из которых равен числу a.

Запись a n читается как: а в степени n, или n-ая степень числа a.

А вот следующие записи можно произносить по-разному:

a 2 – её можно произносить «а в квадрате» или «а во второй степени»;

a 3 – её можно произносить «а в кубе» или «а в третьей степени».

Стоит отметить, что особые случаи возникают, если показатель степени равен нулю или единице:

степенью числа а с показателем n = 1 является само это число:

любое число в нулевой степени равно единице:

ноль в любой натуральной степени равен нулю:

единица в любой степени равна 1:

Выражение 0 0 (ноль в нулевой степени) считают неопределенным.

Примеры. Возведём в степени:

При решении задач, нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.

Рассмотрим несколько примеров.

Возведём в степень

2 5 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 32

2,5 3 = 2,5 ∙ 2,5 ∙ 2,5 = 15,625

Основание степени может быть любым числом – положительным, отрицательным или нулём.
При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа, в результате может получиться как положительное число, так и отрицательное число. Это зависит от того, чётным или нечётным числом был показатель степени.

(-5) 4 = (-5) ∙ (-5) ∙ (-5) ∙ (-5) = 625.

Рассмотрим такой пример: 4 2 ∙ 5 2 = 4 ∙ 4 ∙ 5 ∙ 5 = (4 ∙ 5) ∙ (4 ∙ 5) = (4 ∙ 5) 2 = 20 2 = 400.

Данный пример подтверждает справедливость следующего свойства степеней:

Произведение степеней с одним и тем же показателем равно степени с тем же показателем и основанием, равным произведению оснований:

Этот пример подтверждает справедливость следующего свойства степеней:

Произведение степеней с одним и тем же основанием это степень с тем же основанием и показателем, равным сумме показателей этих степеней, т.е.

Наконец, рассмотрим равенство:

Это равенство подтверждает справедливость следующего свойства степеней:

Степень степени числа равна степени того же числа с показателем, равным произведению показателей этих степеней, т.е.

Разбор решения заданий тренировочного модуля

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Источник